橫風下高速列車突入隧道瞬變壓力及列車風

王 磊， 駱建軍， 李飛龍

(1. 北京交通大學 土木建筑工程學院, 北京 100044； 2. 北京交通大學 城市地下工程教育部重點實驗室, 北京 100044;3. 北京交通大學 結構風工程與城市風環境北京市重點實驗室, 北京 100044)

高速列車駛入隧道時會產生壓力波[1]，初始壓縮波大小與列車速度的平方成正比[2-4]。隨著高速列車運行速度越來越高，高速鐵路隧道空氣動力學效應將更加顯著[5]。由于空氣黏性效應，列車運動時會產生強勁的列車風[6]。氣動壓力和列車風的共同作用會對人員安全及隧道內設備產生影響，甚至嚴重威脅列車運行安全。

高速鐵路隧道氣動效應已經受到越來越多國內外學者的重視。Niu等[7]回顧了列車通過隧道引起的氣動效應，并指出影響氣動效應的因素包括列車形狀、列車長度、車速、隧道長度、阻塞比、通風豎井、環境風和列車交會等。Gilbert等[8-11]分別采用現場試驗和縮比試驗研究了列車通過隧道內壓力波的變化規律，得到壓力波峰值與列車速度之間的關系。除對氣動壓力進行研究外，隧道內氣體流動也備受關注。Ko等[12]通過動模型試驗，研究了列車通過封閉空間和隧道過程中的瞬態氣體流動。Sakuma等[13-16]采用實車試驗方法對隧道內列車風分布規律進行了研究，表明氣動載荷是導致列車產生橫向振動的主要原因。劉堂紅等[17-18]采用實車試驗和數值模擬方法研究表明復線隧道內的氣動壓力變化規律與單線隧道有很大差異。

在我國西部山區，為了保證線路的平順性，橋梁與隧道、平地與隧道相連接的情況比較常見。目前國內外學者的研究主要集中在無風環境下單列高速列車通過隧道或隧道內兩車交會時的氣動特性，關于橫風下高速列車駛入過程中隧道內氣動效應的研究較少。Chen等[19-20]研究了環境風對單車通過隧道、隧道內兩車交會時壓力波的變化，不過他們假設環境風風向與列車運動方向平行。實際上，橫風下列車駛入隧道導致作用在列車上的氣動荷載發生突變，嚴重影響列車的安全和乘客的舒適性。因此對橫風下列車突入隧道過程進行研究可以深入理解橫風對列車氣動性能的影響機理，增強對橫風-列車-隧道相互作用的認識，對最終提出改善列車氣動性能的防護措施具有重要研究意義。

為此，本文基于高速列車橫風作用下流場的非定常、可壓縮湍流特性，建立橫風-列車-隧道模型進行仿真計算，研究橫風條件下列車突入隧道內氣動壓力和列車風的變化規律，以揭示橫風-列車-隧道之間的相互作用機理。此外將計算結果與無風環境進行對比分析，研究橫風對列車周圍流場結構的影響，得到橫風對隧道內瞬變壓力和列車風變化的影響機理。

1 數值模型

1.1 控制方程

橫風條件下高速列車運動引起的氣體流動是具有黏性、可壓縮性的非定常三維湍流流動，需要遵循質量守恒定律、動量守恒定律和能量守恒定律。

直角坐標系下微分形式的質量守恒方程為

(1)

式中，t、ρ、xi、ui分別為時間、密度、坐標分量和速度分量。

動量守恒方程，即可壓縮N-S方程

(2)

式中：δij為克羅內克符號，當i=j時，δij=1.0，當i≠j，δij=0；μ為動力黏性系數。

能量守恒方程為

(3)

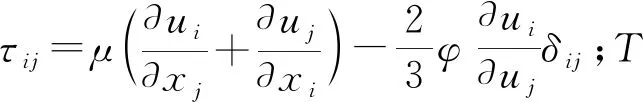
假定空氣為完全理想氣體，狀態方程為

p=ρRT

(4)

式中，R為氣體常數。

以式(1)～式(4)中含有ρ、p、T、ui三分量共6個未知數，可以組成一個封閉方程組進行求解。

1.2 幾何模型與邊界條件

CRH380A高速列車最高運營速度為400 km/h，本文以8車編組CRH380A列車為對象進行研究。列車寬度、高度分別為3.38 m和3.7 m，橫截面積為11.2 m2。列車頭尾車相同，頭尾流線型長度為12 m，總長度為203 m，如圖1所示。忽略受電弓、轉向架等細部結構，模型為光滑車體。隧道采用中國高速鐵路標準雙線隧道，凈空面積為100 m2，阻塞比為0.112，線間距為5.00 m，車體底部間隙高度為0.20 m，如圖2所示。以列車高度為特征長度，列車速度為400 km/h，雷諾數Re=2.6×107。

(a) 側視圖

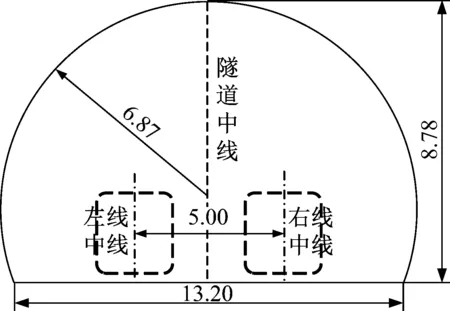
圖2 隧道斷面示意圖(m)

為保證列車周圍流場在駛入隧道前得到充分發展，車頭鼻尖到隧道入口初始距離為100 m。為降低計算成本，選取500 m長隧道進行計算。隧道入口、出口空氣計算域的長×寬×高分別取400 m×250 m×80 m和100 m×100 m×80 m。模型采用大地參考坐標系，原點位于隧道入口處，其中x軸沿隧道縱向，y軸和z軸分別代表橫向和豎向。計算域采用結構化網格離散，列車表面網格最小尺寸為0.02 m，隧道壁面網格最小尺寸為0.2 m，離散后網格不少于1 900萬，隧道洞口處網格如圖3所示。

圖3 隧道入口網格

列車表面、隧道壁面采用無滑移邊界條件，隧道壁面當量粗糙度高度取為5 mm[21]，列車表面粗糙度高度取為0.045 mm[22]。高速鐵路隧道洞口一般采用帽檐斜切式結構，能夠顯著降低列車駛入隧道產生的氣動效應。本文基于最不利原則考慮，隧道出入口簡化為垂直平面，設置為無滑移壁面邊界。隧道入口計算域右側表面采用均勻風速度入口邊界，Vw=24.4 m/s，對應9級大風；左側、前側及頂部表面均采用壓力出口邊界，壓力取值標準大氣壓。出口側空氣域頂部、左右側及后側表面采用壓力遠場邊界，模型尺寸及邊界條件如圖4所示。列車中線到橫風入口距離為50 m，到左側壓力出口距離為200 m，能夠保證列車背風側渦流結構充分發展。入口計算域的阻塞比為2.3%，滿足BS EN 14067-6:2018《歐洲鐵路標準》阻塞比不超過5%的要求。在列車運動前，首先進行穩態計算，待流場穩定后再進行瞬態計算。為降低計算成本，提高計算效率，采用采用滑移網格技術模擬列車運動[23-26]。

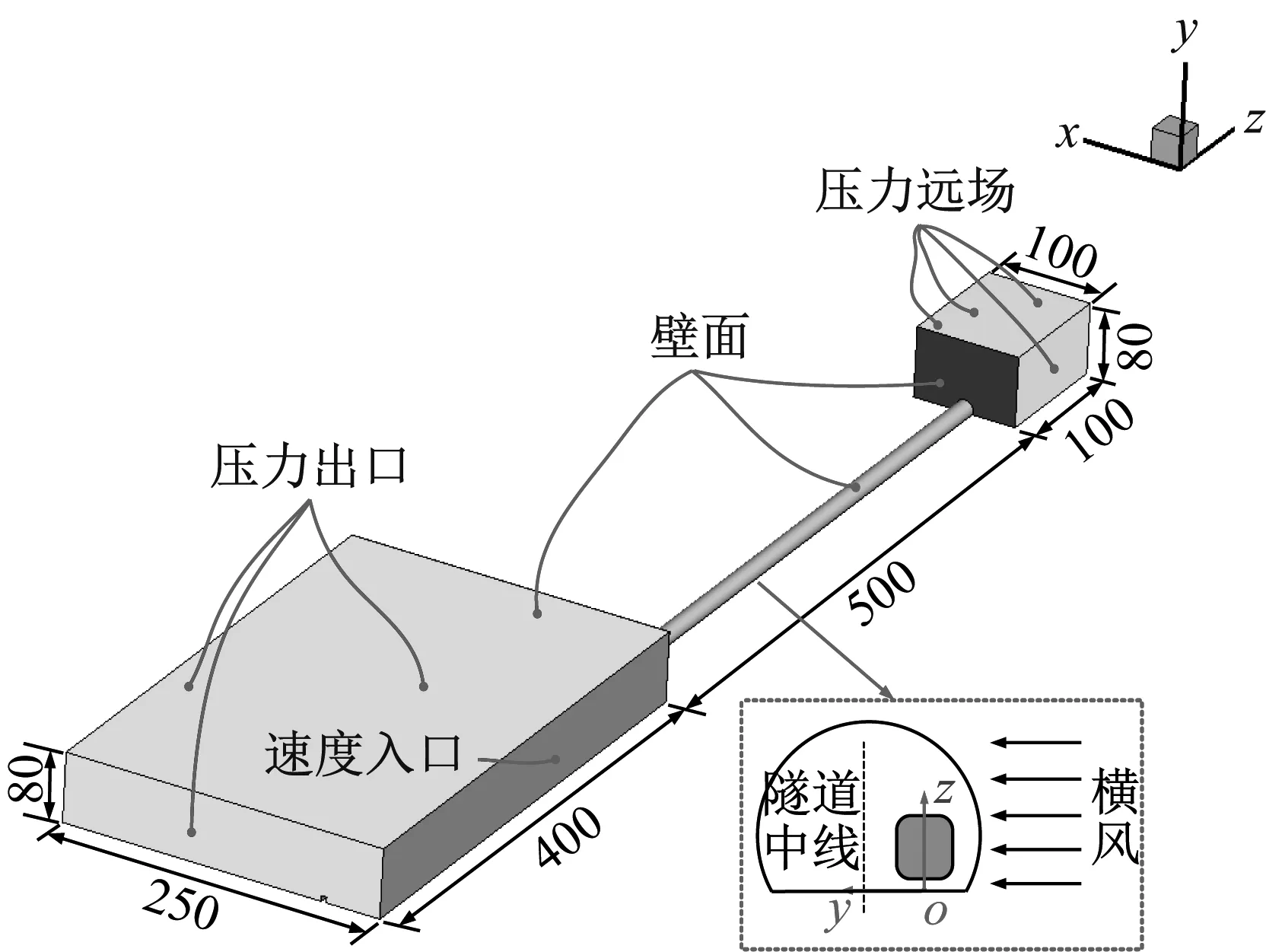
圖4 模型尺寸及邊界條件(m)

1.3 測點分布

沿隧道縱向設置若干個監測斷面，由于橫風對隧道入口附近影響較大，因此在入口附近監測斷面加密，距隧道入口分別為0、10 m、20 m、50 m、100 m和150 m，橫斷面測點布置如圖5所示。需要說明的是，為了更加清楚的進行結果分析，只選擇其中部分測點進行研究。

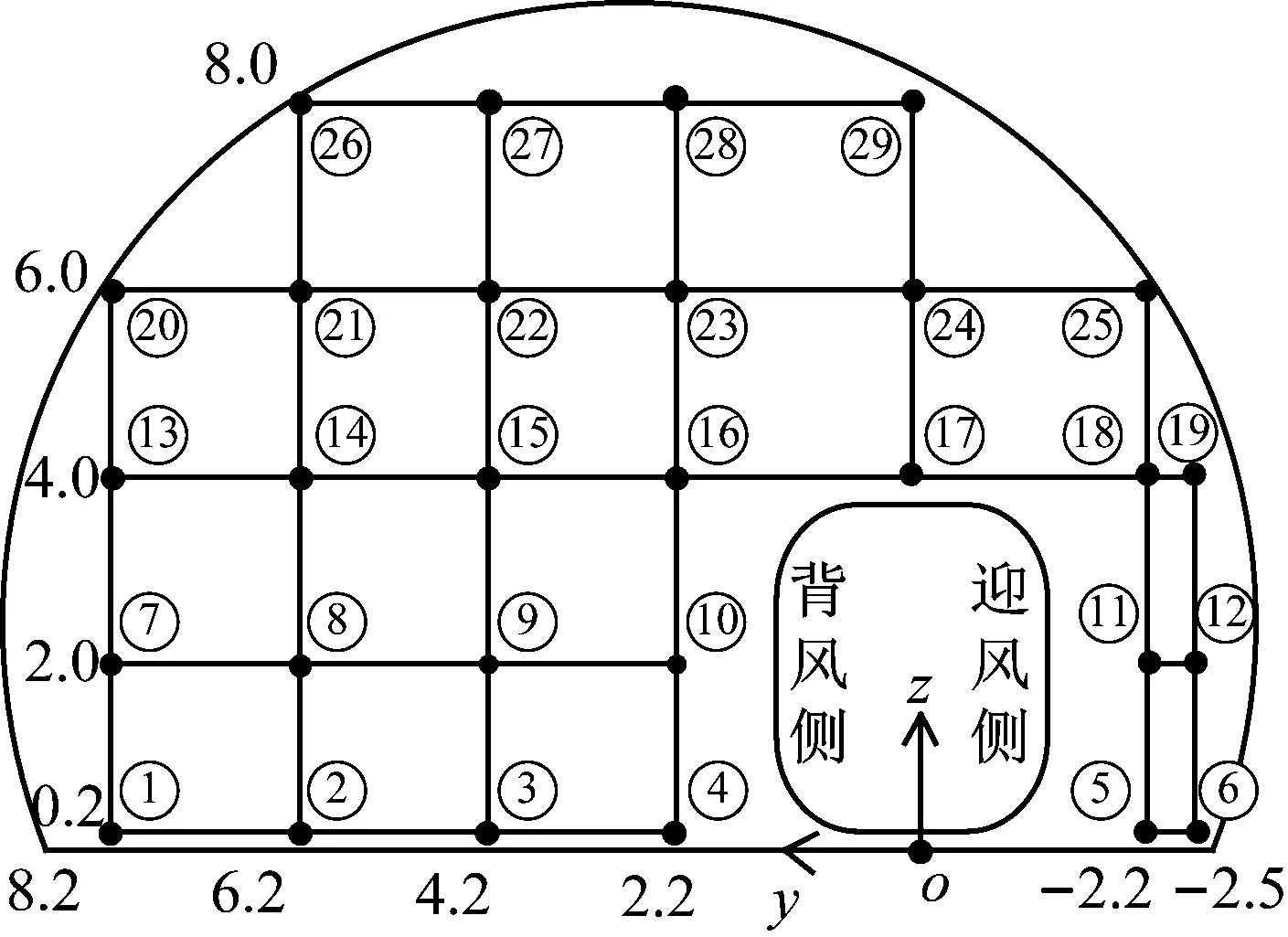
圖5 測點布置圖(m)

1.4 求解方案

列車在隧道內運行時產生三維、可壓縮、非定常流動[27-28]，本文采用非定常、黏性、可壓縮N-S方程和RNGk-ε雙方程湍流模型進行仿真模擬，該模型已被廣泛證明能夠有效應用于高速鐵路隧道氣動效應研究[29-31]，足以驗證其計算結果的可靠性。

本文計算采用流體計算軟件Fluent，控制方程通過有限體積法離散，壓力-速度耦合采用SIMPLE算法，對壓力采用迭代法修正。對流-擴散項離散采用二階迎風格式，時間導數采用一階隱式方法進行離散。計算時間步長取為1×10-3s，每個時間步迭代次數為20次。

2 模型驗證

本文采用國內某標準雙線高速鐵路隧道實車試驗驗證本文數值方法的準確性。試驗列車采用CRH380A列車編組，列車試驗速度為350 km/h。隧道全長2 908 m。數值驗證中隧道形式與實際保持一致，長度為2 900 m，求解方法與1.4節相同，列車類型、編組形式及車速與現場試驗保持一致。沿隧道縱向設置氣動壓力測點，對列車通過階段測點壓力變化進行監測。

為方便空氣動力學研究，一般對計算結果采用無量綱系數進行分析。氣動壓力采用壓力系數Cp=p/0.5ρv2，其中p、ρ、v分別為氣動壓力值、空氣密度和列車速度。距離隧道入口250 m處的氣動壓力系數實測與數值計算曲線，如圖6所示。經過對比，現場實測與計算結果變化規律基本一致，吻合良好。現場實測與數值計算正、負壓力系數最大值分別相差12.1%和8.6%，均在工程誤差允許范圍之內。現場實測與數值計算主要差別出現在列車完全駛入隧道(t=20 s)時，這可能是由于現場試驗環境的不確定引起的。

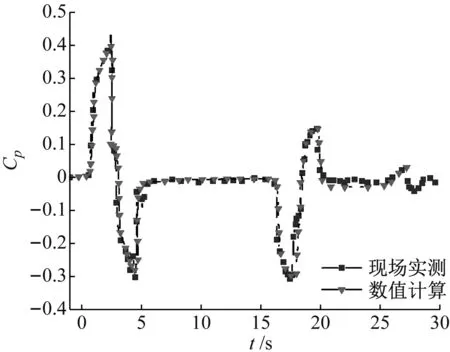
圖6 現場實測與計算結果對比

為進一步驗證橫風條件下數值模型的可靠性，CRH380A兩編組列車以350 km/h的速度在橫風風速為30 m/s環境中運行時列車周圍的流場結構，如圖7(a)所示。文獻[32]中CRH3橫風下露天行駛時列車周圍流場結構，如圖7(b)所示。對比可知，橫風條件下，脫落渦均在頭車流線型背風側產生，兩者流場結構基本相同。

(a) CRH380A

綜上所述，無論有無橫風情況，本文采用的數值模型及求解方法均是可靠的。

3 結果分析

3.1 瞬變壓力

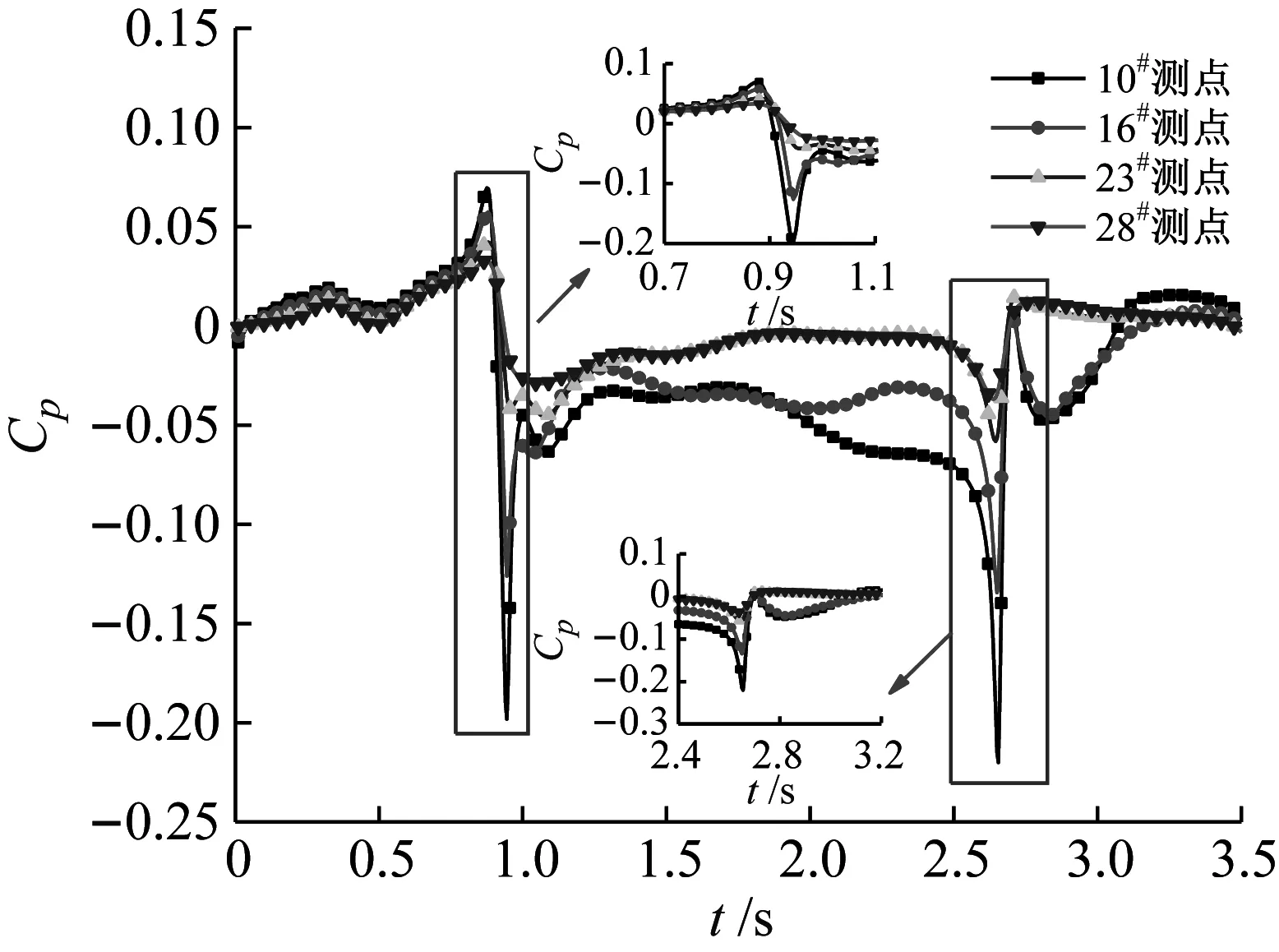
列車駛入過程中隧道入口和距入口50 m處測點壓力系數變化曲線，如圖8、圖9所示。圖8(a)、圖9(a)為有橫風情況，圖8(b)、圖9(b)為無橫風情況。對比圖8(a)、圖9(a)可知，列車在橫風下駛入隧道過程中(t=0.9～2.7 s)，入口處各測點壓力系數差異顯著。在車尾駛入隧道(t=2.7 s)前，迎風側11#測點壓力系數均為正值，背風側7#～10#測點壓力系數均為負值，并且背風側測點壓力系數波動程度更加嚴重。

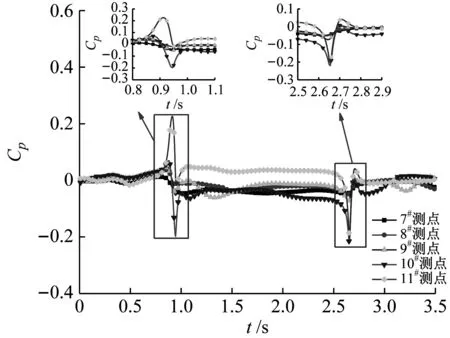
(a) 橫風

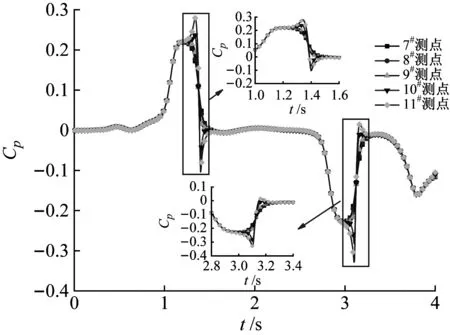
(a) 橫風

測點瞬變壓力變化規律與列車位置有關。頭車駛入隧道時(t=0.9 s)，入口處迎風側11#測點正壓力系數最大，而背風側10#測點負壓力系數最大，意味著受列車阻擋迎風側氣流速度降低，壓力增大，在列車表面發生流動分離，背風側流速增加，壓力值減小，并且測點距離列車越近，壓力系數絕對值越大，受橫風影響程度越大。當尾車駛入隧道時(t=2.7 s)，由于列車阻擋效應消失，所有測點壓力系數迅速反向增大。

對比圖8可得不同條件下隧道入口測點壓力系數峰值，如表1所示。表1中：下標H、R為頭、車尾駛入隧道；max、min為最大值和最小值。分析可知，在頭車駛入過程中，橫風對背風側7#～9#測點的Cp-Hmax影響較小，Cp-Hmin影響較大。隨著越來越靠近列車，橫風對測點壓力系數最小值的影響程度降低，10#測點有無橫風時最小壓力系數Cp-Hmin之比為1.64，而7#測點壓力值之比為16.67，究其原因是距離列車愈近，列車運動引起的列車風越大，影響程度增強，相反的，橫風作用影響程度逐漸降低，與無橫風情況下的差別減小。

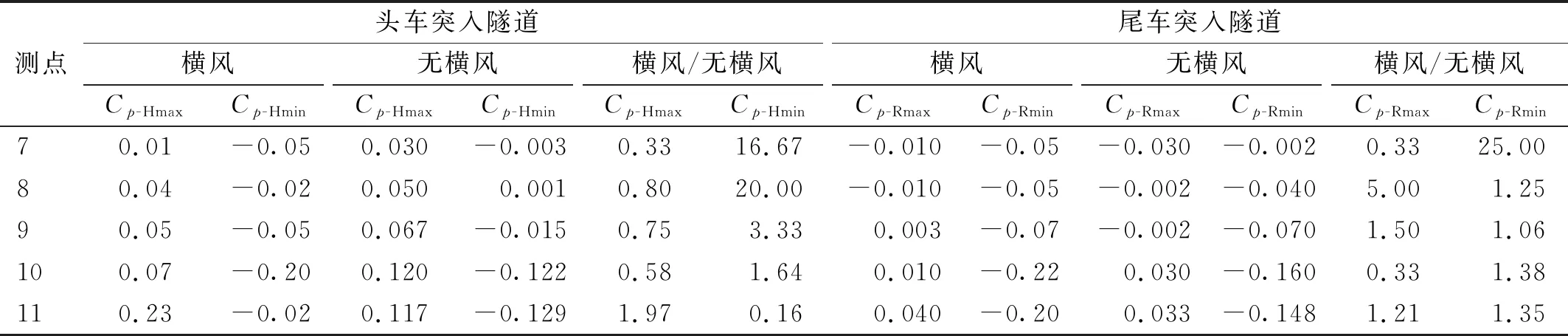
表1 列車突入過程中入口處壓力系數峰值

在橫風作用下，11#測點的壓力系數最大值Cp-Hmax、最小值Cp-Hmin分別為0.23和-0.02，無橫風時11#測點的Cp-Hmax、Cp-Hmin分別為0.117和-0.129，表明與無橫風時相比，橫風導致列車迎風面正壓力系數迅速增大，負壓力系數急劇降低，列車迎風面主要受壓力作用。

尾車駛入隧道時(t=2.7 s)，對比分析可知橫風對各測點壓力系數的影響相對較小。綜上可知，在橫風條件下，頭車突入隧道對入口處氣動壓力變化的影響更加顯著。

頭車駛入過程中10#、11#測點壓力系數與到入口距離的關系曲線，如圖10所示。由圖10可知，背風側10#測點初始壓縮波負峰值絕對值隨著到入口距離增大而減小，正壓力峰值與峰-峰值大小均隨到入口距離增大而增大，最終在距入口約50 m左右趨于穩定。對于迎風側11#測點，無論初始壓縮波正負峰值還是峰-峰值，數值大小均隨著到入口距離增加而增大，最終在距離隧道入口約50 m處達到基本穩定，幾乎不受到入口距離的影響。由此可知，當橫風風速為24.4 m/s時，影響隧道內氣動壓力的范圍不超過50 m。此外，有關橫風風速、車速及風向與隧道內橫風影響范圍的關系需要進行深入研究。

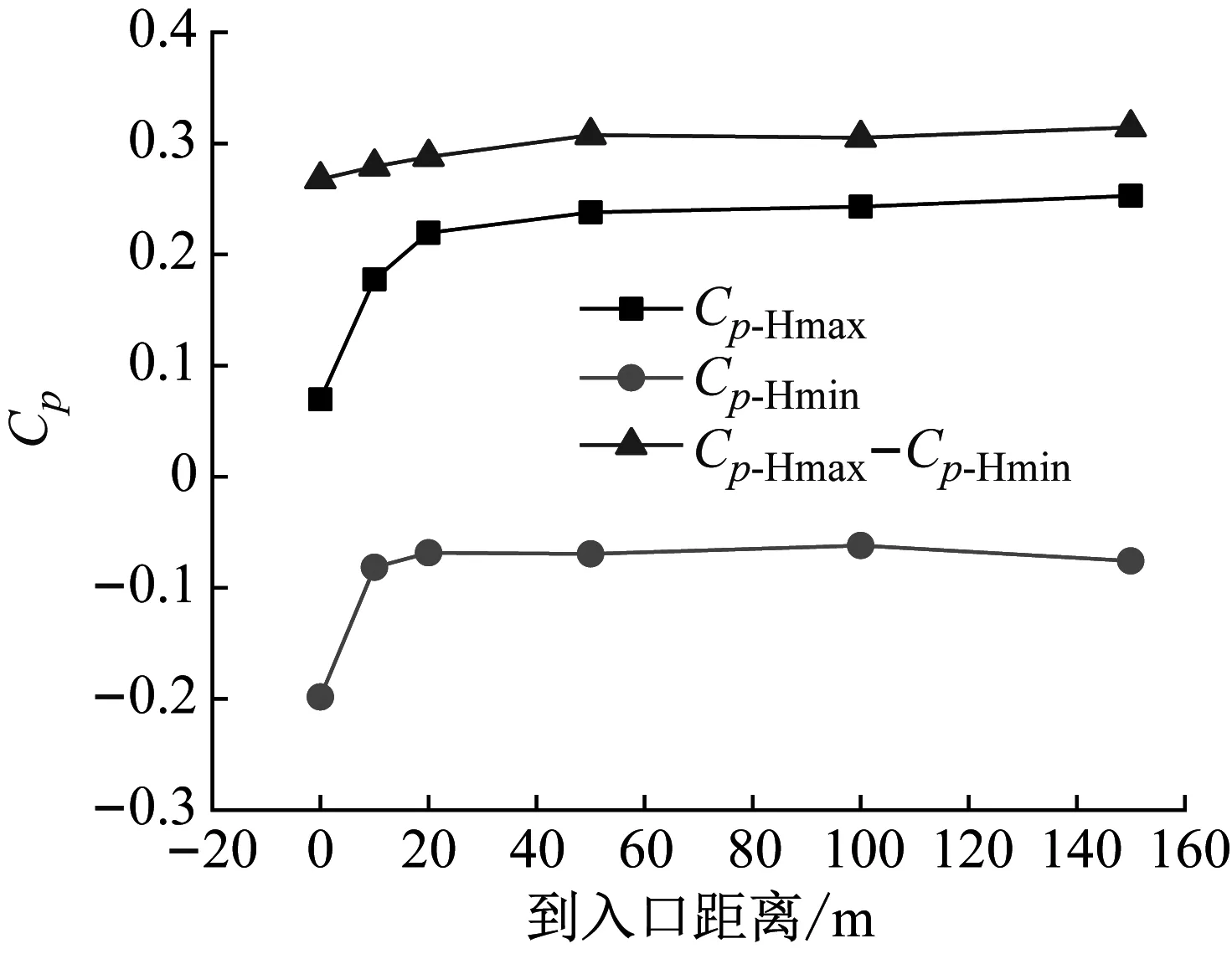
(a) 10#

入口處垂向布置測點的壓力系數變化曲線，如圖11所示。由圖11可知，越靠近軌面，氣動壓力系數峰值越大，波動程度越嚴重，這與無橫風條件下測點的氣動壓力規律相似。聯合圖8(a)分析可知：入口處背風側氣動壓力為負值，迎風側氣動壓力值為正；無風時壓力基本關于列車中線對稱分布，橫風環境明顯改變了入口處氣動壓力變化規律。

(a) 背風側

3.2 列車風

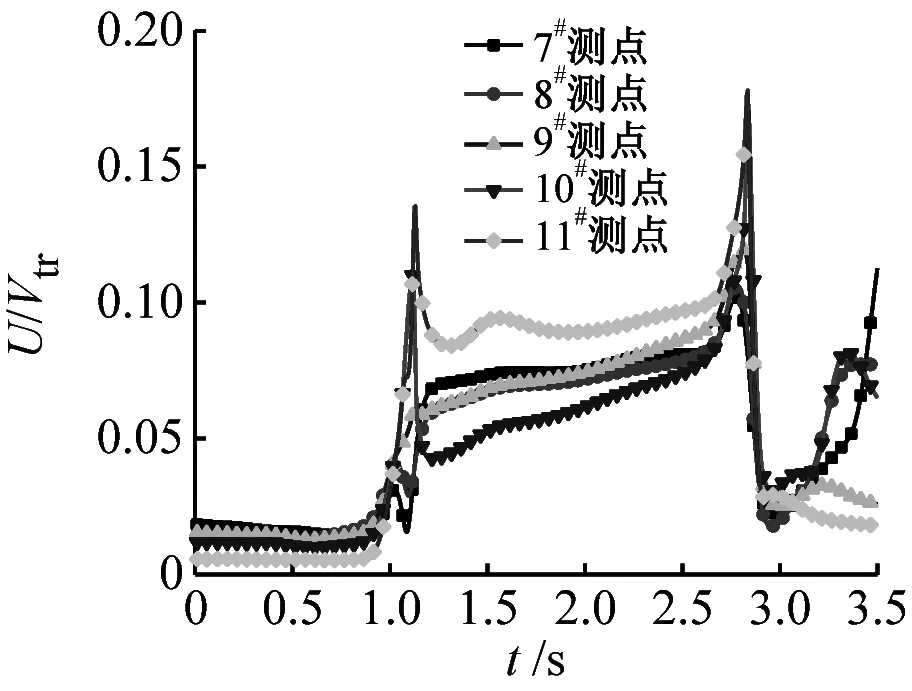
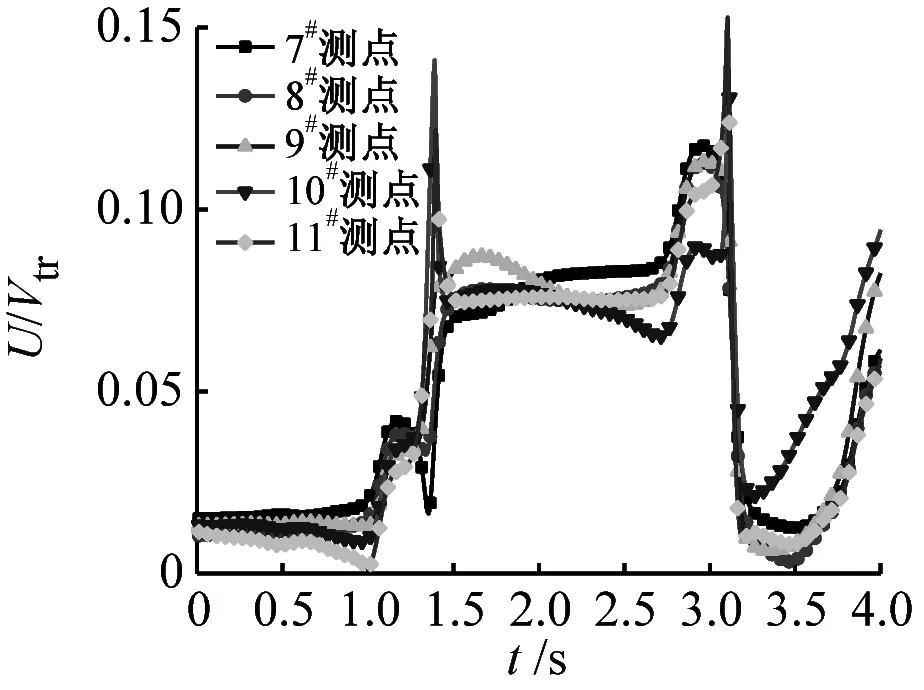
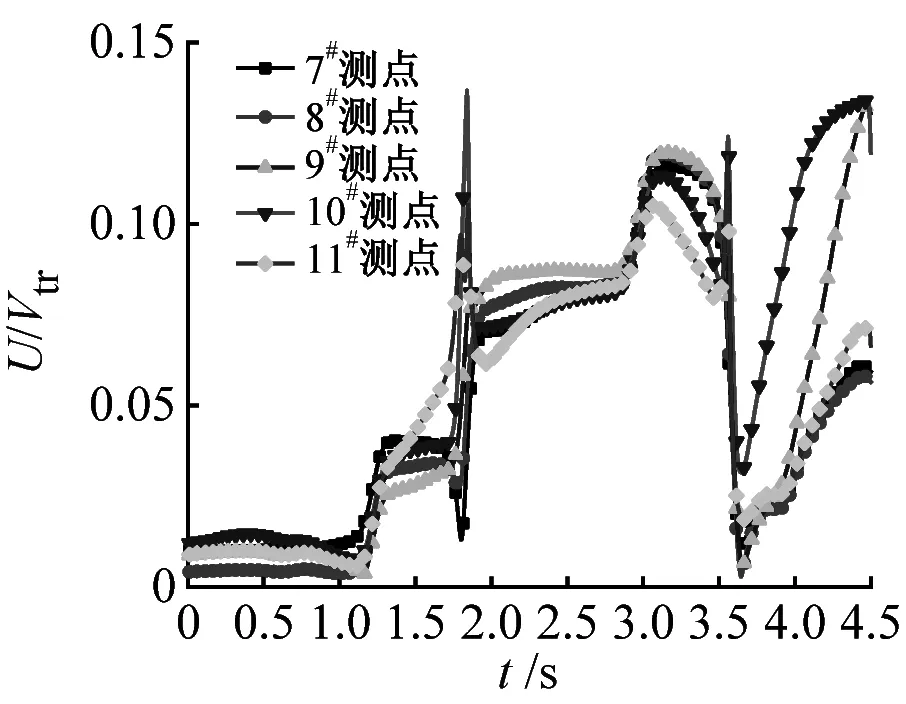
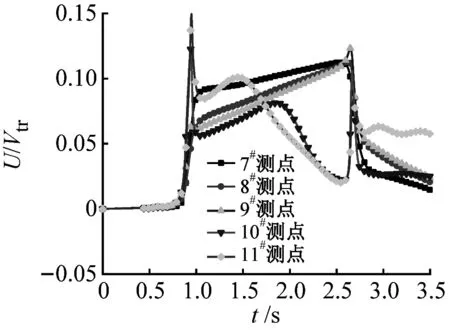
列車運動會帶動一定范圍內氣體流動，稱之為列車風。將列車風合速度U沿x、y、z坐標軸分解可得橫向分量u、垂向分量v和縱向分量w，并且風向與坐標軸正向相同，風速值為正，反之為負，可參考圖4所示。為便于對比分析，對列車風合速度U、橫向分量u、垂向分量v和縱向分量w分量進行無量綱化處理，表達式分別為U/Vtr、u/Vtr、v/Vtr和w/Vtr，其中Vtr為列車速度。現研究橫風對隧道內列車風的影響規律。不同位置測點列車風分量隨時間的變化曲線，如圖12～圖16所示。無橫風時隧道入口處測點的列車風分量時程變化曲線，如圖17所示。

無橫風時，在車頭鼻尖駛入前(t=0.9 s)，各測點的列車風分量均為0，只有在車頭通過以后，各測點列車風分量的差異開始顯現，并且垂向分量v遠小于橫向分量u和縱向分量w。對比圖12和圖17，各測點列車風分量隨時間的變化規律發生明顯變化，表2為有無橫風情況下入口處各測點的列車風分量最大值。當車頭進入隧道時，橫風在列車頂部及底部發生流動分離，在列車背風側形成隨時間、空間變化的旋渦，引起列車背風側測點列車風合速度U、橫向分量u和縱向分量w明顯增大，而垂向分量v變化不顯著，例如橫風下9#測點列車風U、u、w分別是無風時對應列車風分量的3.5倍、4.2倍和1.7倍，說明橫風條件對入口處測點的列車風橫向分量u影響最大。橫風對車頭駛入時迎風側測點的列車風分量的影響不顯著，值得注意的是，11#測點列車風橫向分量流動方向不同。

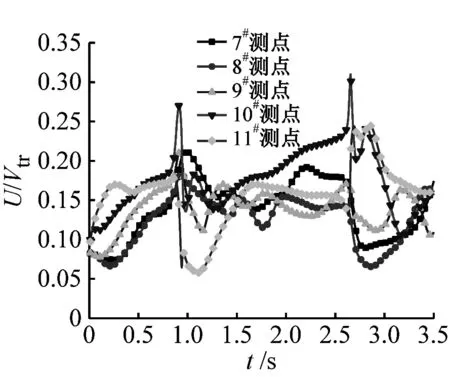
(a) U

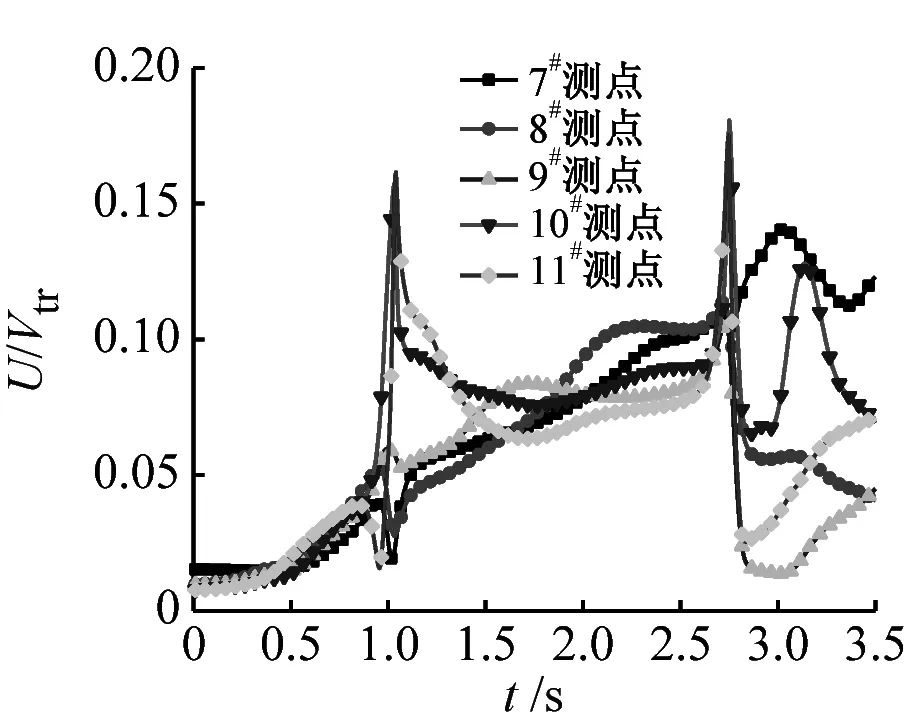
(a) U

(a) U

(a) U

(a) U

(a) U

表2 不同橫風情況下入口處測點列車風分量最大值

當車尾駛入時(t=2.7 s)，列車阻擋效應逐漸消失，橫風對背風側測點的列車風分量的影響不明顯，而對迎風側測點列車風分量U、橫向分量u和縱向分量w的影響較大，這與橫風對車頭駛入時列車風分量的影響規律正好相反。從圖12～圖16還可得出，在列車車身駛入隧道過程中(0.9～2.7 s)，迎風側測點的列車風分量波動程度較小，而背風側測點的列車風分量隨時間變化的波動程度非常明顯，與氣動壓力變化規律相同。

對圖12～圖16進行對比分析，隨著到入口距離的增大，同一測點的列車風分量幅值及波動程度逐漸降低。由以上分析可得，橫風分列車風U、橫向分量u及縱向分量w影響較大，因此以10#、11#測點為研究對象，分析橫風對隧道內列車風的影響范圍。

車頭駛入時10#測點、車尾駛入時11#測點的列車風分量最大值與測點位置的關系曲線，如圖18所示。由圖18(a)可知，車頭駛入時，由于隧道遮蔽效應導致列車風U、橫向分量u隨著到入口距離增加先迅速減小，后緩慢增大，距離入口50 m時，列車風分量基本不變，縱向分量w先增大后減小，這是因為橫風對隧道內氣體外流有一定阻擋作用，導致入口處10#測點縱向分量w值最小。隨著到入口距離增大，隧道阻擋效應減弱。當距離入口50 m時，縱向分量w逐漸趨于穩定。由圖18(b)可知，車尾駛入時，11#測點的列車風分量最大值均隨著到入口距離增加而減小，當測點距入口50 m時，列車風分量趨于穩定。由此可知，無論是迎風側還是背風側，橫風對隧道內列車風的影響距離為50 m，與3.1節研究結果一致。

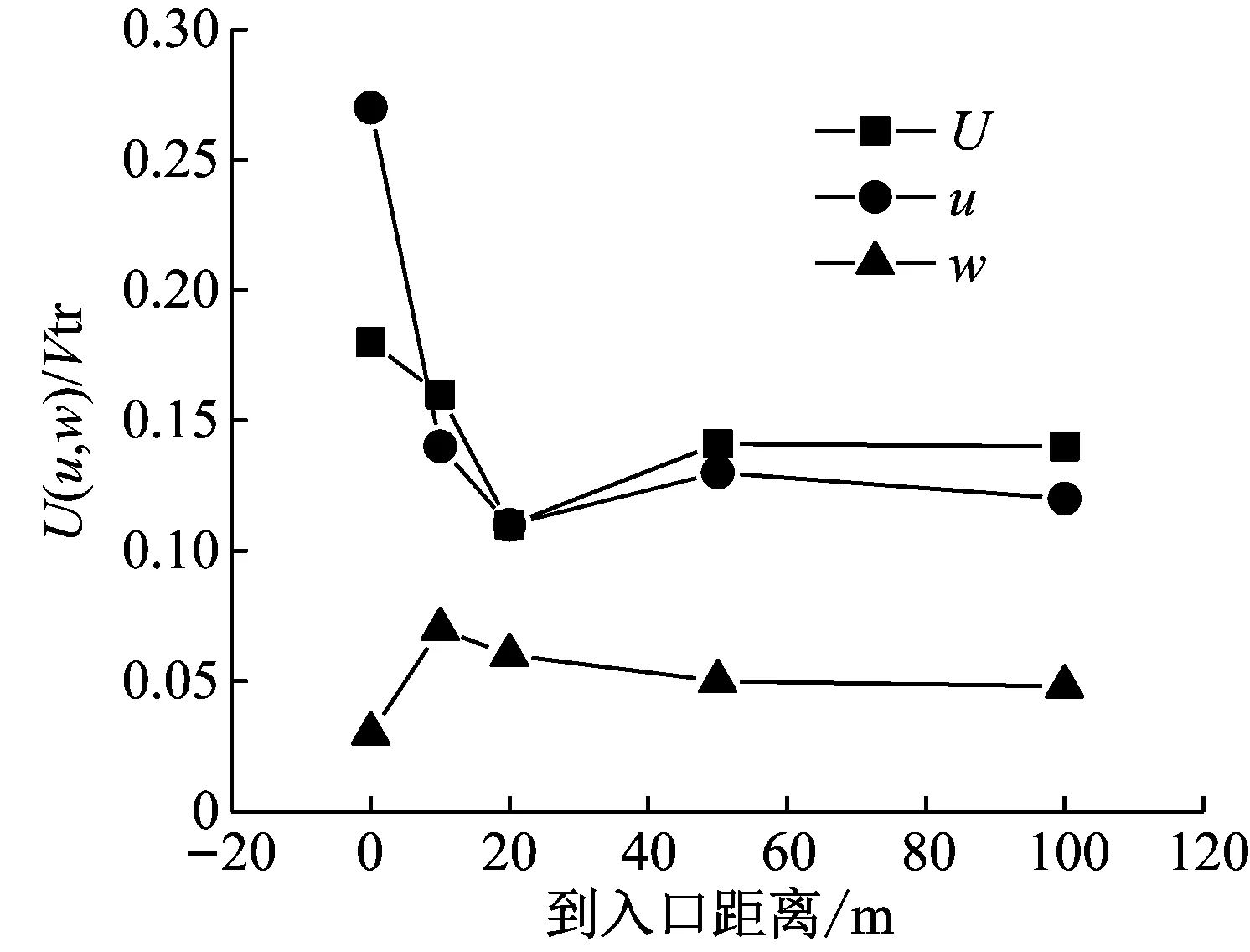
(a) 車頭駛入時10#測點

3.3 流場分布

為進一步分析列車在橫風條件下突入隧道瞬變壓力及列車風的突變機理，以一半列車長度駛入隧道(t=1.8 s)為例進行分析。兩種情況下列車周圍的流線分布及列車風橫向分量u云圖，如圖19、圖20所示。z=2.0 m水平面流場分布圖，見圖19(a)、圖20(a)。對比可知，橫風對列車周圍流場分布的影響非常大。當列車由橫風突入隧道時，由于隧道的屏蔽效應，隧道內背風側的渦結構迅速消散，隧道入口處的渦旋結構向車尾延伸，并向背風側偏轉，伴隨著列車風分量u的劇烈變化，表現出明顯的湍流特性。在橫風和列車運動作用下，迎風側部分氣體流入隧道內部從而在隧道內形成順時針的旋渦，見圖19(a)。無橫風時，流線由車頭流向車尾，流場基本關于列車中線對稱分布。列車駛入僅在在列車尾部和隧道入口外部產生渦旋結構，見圖20(a)。

分析圖19(b)～圖19(d)可知，在橫風下，入口處迎風側氣流速度u最大，隨著到入口距離增加，列車風橫向分量u逐漸減小。氣流在列車頂部產生分離，在背風側形成隨時間、空間變化的旋渦，引起氣動壓力和氣流速度大幅度波動。對比圖20(b)～圖20(d)可知，無橫風時，僅在列車頂部和底部產生小尺度流動分離，橫向氣流速度u變化不大。

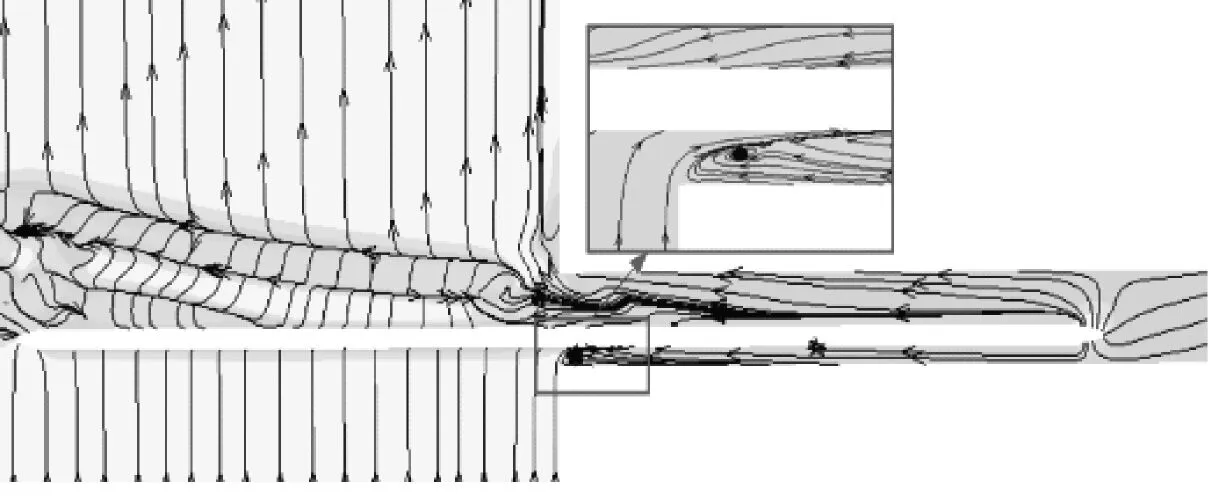
(a) z=2 m

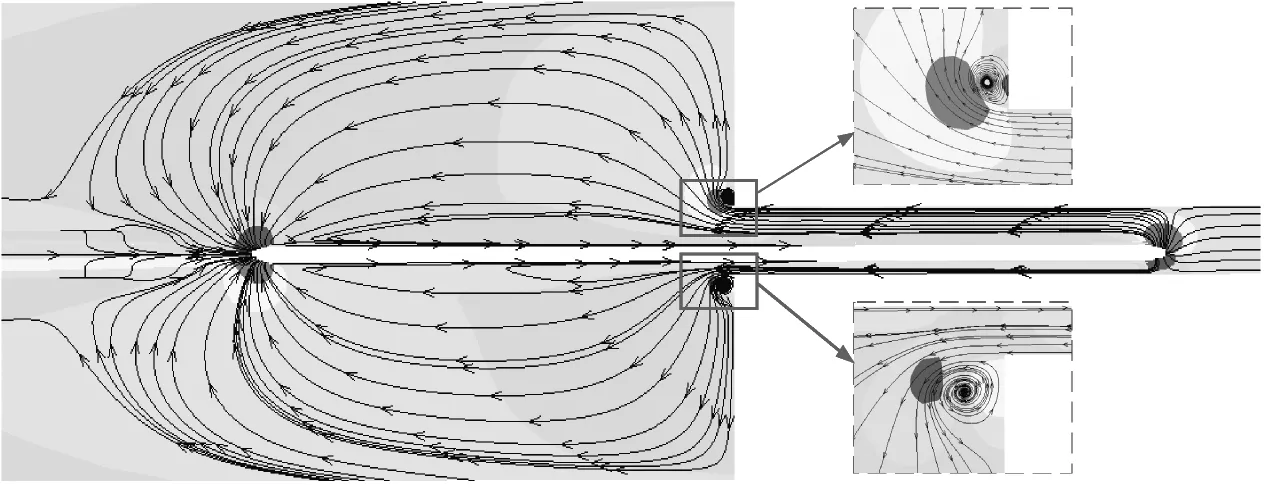
(a) z=2 m

4 結 論

(1) 列車在橫風中高速駛入時隧道入口附近的氣動壓力規律發生明顯變化。在尾車完全駛入隧道前，橫風對列車背風側壓力變化影響較大，當列車完全進入隧道后橫風對氣動壓力的影響不大。此外，頭車突入隧道對入口處氣動壓力變化的影響更加顯著

(2) 列車駛入隧道不同階段，橫風效應對列車風的影響規律不同。車頭突入隧道時，橫風對列車背風側列車風分量的影響較大，車尾完全駛入時，橫風對列車迎風側的列車風分量的影響比較嚴重。

(3) 橫風對列車由明線駛入隧道過程中隧道內的氣動壓力和列車風的影響范圍有限。當列車速度為400 km/h，橫風速度為24.4 m/s時，橫風影響隧道內氣動壓力和列車風的有效距離為50 m。

(4) 當列車由橫風突入隧道過程中，由于隧道的遮蔽效應，隧道內列車風渦旋結構迅速消散。在入口處列車背風側形成的渦結構向車尾延伸，并向背風側偏轉。橫風作用是氣動壓力和氣流速度波動的根本原因。