基于EEMD-SDCCⅠ-HMM的水電機組振動故障識別方法

胡 曉， 肖志懷,2， 劉 東， 趙文利， 王 海， 蔣文君

(1.武漢大學 動力與機械學院，武漢 430072；2.武漢大學 水力機械過渡過程教育部重點實驗室，武漢 430072；3.武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072；4.國家能源集團新疆開都河流域水電開發有限公司，新疆 庫爾勒 841000)

隨著水電機組復雜化程度和電站智能化水平日益提高，水電機組故障診斷技術也越來越受到重視。故障診斷主要包括信號檢測及預處理、故障信號分析及其特征提取、故障類型識別及故障處置決策四大部分[1]。由于水電機組多數故障都在振動信號中有所反映，因此對振動信號進行分析和特征提取是十分必要的[2]。一般情況下，可通過時頻分析或圖像處理[3]的方法得到故障信號特征，如幅值、頻率、相角和軸心軌跡等。當前較為流行的時頻分析方法包括小波變換、經驗模態分解(empirical mode decomposition，EMD)等。其中，EMD作為一種自適應信號處理方法，避免了小波基和分解層數的選擇，被認為是時頻分析領域的重大突破[4-5]。然而，當信號間斷或受干擾時，EMD分解中常出現模態混疊現象，嚴重影響信號的后續分析[6]。為此，Wu等[7]提出了集合經驗模態分解(ensemble empirical mode decomposirion，EEMD),能夠抑制信號分解過程中局部極值在短時間內的頻繁跳動，從而解決了因間斷事件引起的模態混疊問題。

若故障信號成分復雜或噪聲較多，可將時頻分析方法與其他檢測指標相結合以獲取信號中的有效信息，如許多學者采用奇異值、近似熵、樣本熵等可以反映信號中某些變化特性的參數作為故障檢測指標。得到故障特征后，可結合神經網絡、支持向量機和隨機森林等分類方法等進行模式識別。然而受模型自身限制，上述方法通常需要將原始振動信號劃分成等長的數據片段，把每個片段視為單獨的輸入向量進行處理，可能忽略了相鄰輸入向量間的時序關系[8]，造成部分故障信息丟失。隱馬爾科夫模型(hidden Markov model，HMM)能夠對一個時間跨度上的信息進行統計建模和分類,是一種基于統計學理論的動態模式識別工具，對于非平穩和低重復性的信號，具有很強的模式分類能力。近年來HMM受到研究人員的廣泛關注，已經被成功應用于模式識別的眾多領域[9]。

為了充分挖掘水電機組振動信號中能反映機組狀態的關鍵特征，本文結合信號處理領域的EEMD和圖像識別領域中的編碼理論，提出了一種新的水電機組故障特征提取方法。此外，考慮振動信號的時序關系，借助HMM的模式識別功能對編碼所得特征向量分類，達到機組故障識別的目的，最后用試驗驗證了該方法的有效性。

1 水電機組振動信號的IMF特性

1.1 EEMD算法

Huang等通過對白噪聲EMD分解的研究，發現EMD分解的作用類似于二進制濾波器，且白噪聲的能量在其頻譜上呈現均勻分布狀態，故提出了基于噪聲輔助分析的改進EMD方法，即EEMD。EEMD利用白噪聲頻譜均勻分布的特性，在待分析信號中加入白噪聲來補充一些缺失的尺度，一方面使得不同時間尺度的信號自動映射到合適的參考尺度上去;另一方面，零均值高斯白噪聲經過多次平均計算后會相互抵消，于是集成均值的計算結果可視作最終結果，且有效解決了EMD的模態混疊問題。

EEMD算法步驟如下[10]。

步驟1在目標信號x(t)中加入隨機白噪聲(由噪聲等級確定)n(t)，得到待處理信號s(t)

s(t)=n(t)+x(t)

(1)

步驟2對合成信號s(t)進行EMD分解，得到各階本征模態函數(intrinsic mode functions,IMF)

(2)

式中:m為IMF的個數;ci(t)和rm(t)分別為IMF和殘差。

步驟3重復n(n定義為總體平均數)次步驟1和步驟2，每次加入不同的白噪聲。

步驟4將得到的各階IMF的均值作為最終結果。

(3)

研究表明，噪聲等級和總體平均數分別取經驗值0.2和100時，EEMD分解效果較好[11-12]。此外，在EMD分解中，信號兩端點不一定是極值點，直接利用樣條函數計算包絡線會產生端點效應，使分解結果中出現與信號無關的分量，造成信號失真，故本文在步驟2中采用線性外推法進行端點延拓來抑制端點效應。

1.2 IMF的標準差特性

在現代機械故障診斷領域，頻譜分析是常用于判斷故障類型的方法，其本質是捕捉信號中特征頻率的幅值變化。由EMD的原理可知，EMD分解所得IMF是一系列窄帶分量，且每個分量具有不同的頻率成分和帶寬。同時，當被分解信號存在差異時，其相同階數的IMF的截止頻率和帶寬也不相同。由此推斷，IMF的特征參數，如標準差(standard deviation，SD)等可以體現出信號中頻率成分的變化情況，進而成為判斷故障的依據。

為研究IMF的標準差特性，構造如式(4)所示的一般信號，設定采樣頻率為1 024 Hz，采樣時間為1 s。如圖1所示,該信號的標準差是幅值(a)、頻率(f)和相角(b)的函數。從圖1(a)、圖1(b)可以看出，標準差的大小由信號幅值決定，不隨頻率和相角的改變發生變化。在圖1(c)中，當幅值為常數0.03時，相角對標準差的影響比頻率大，但是標準差的變化范圍很小，相比圖1(a)、圖1(b)可以忽略不計。

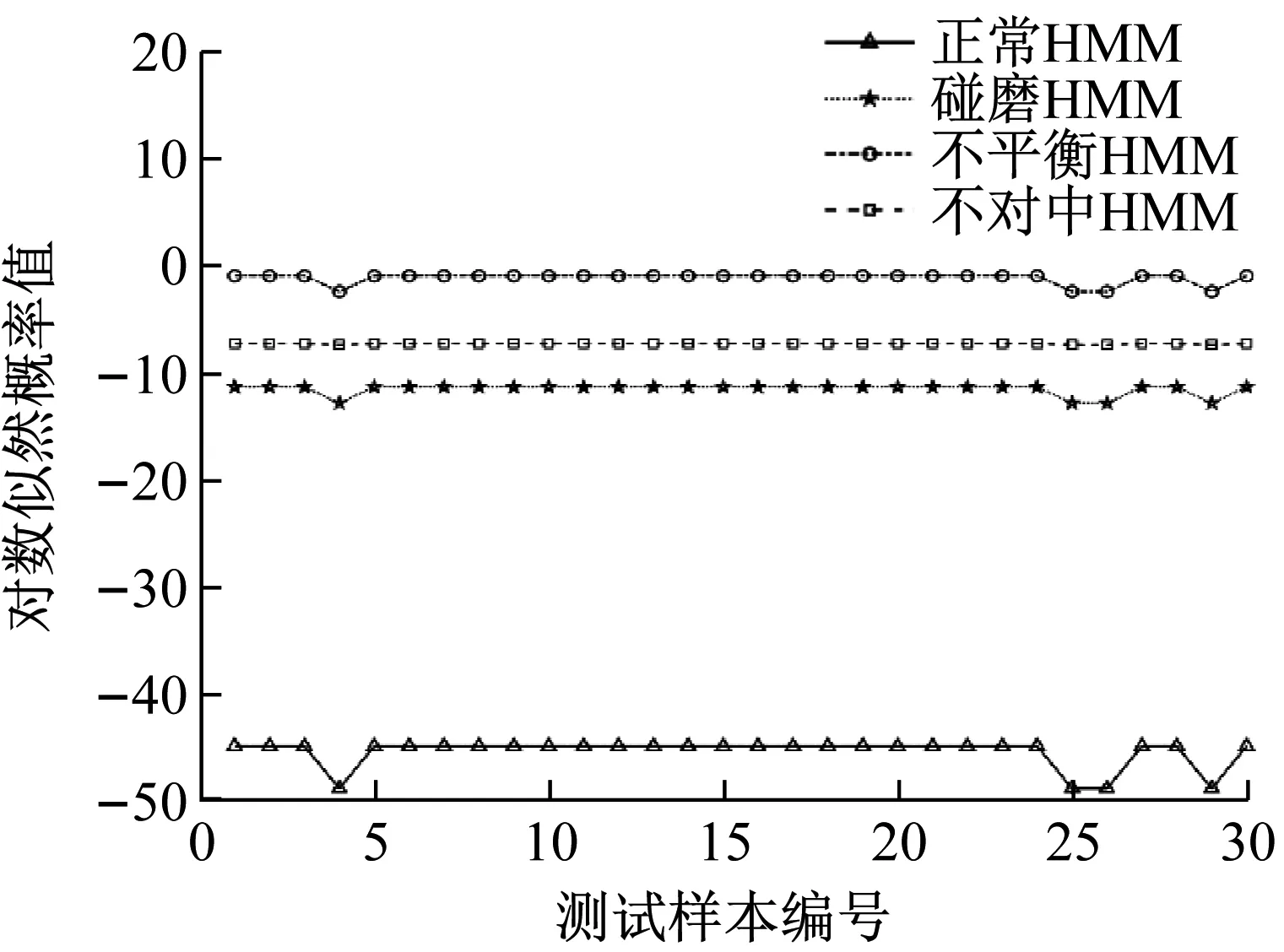
(c) 不平衡狀態測試樣本在各HMM上的輸出值

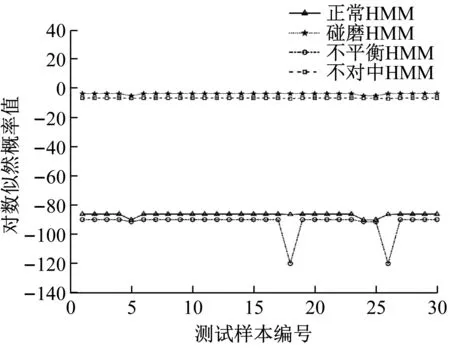
(b) 碰磨狀態測試樣本在各HMM上的輸出值

(a) 正常狀態測試樣本在各HMM上的輸出值

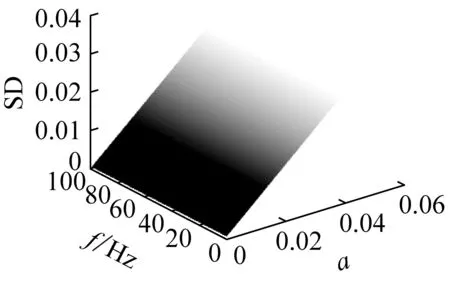
(a) 當b=0時，SD與a和f的關系

y=asin(2πfx+b)

(4)

基于以上分析，進一步研究水電機組振動信號IMF的標準差特性。根據文獻[13]可知水電機組振動頻率與故障原因及機組參數相關，據此可構建不同故障狀態的水電機組振動信號。仿真水電機組參數，機組故障原因與頻率成分的關系分別如表1和表2所示。

表1 仿真機組參數表

表2 水電機組故障原因與頻率成分關系表

構造該機組4種不同故障狀態下含有噪聲時的振動仿真信號如式(5)～式(8)所示。其中:A1為尾水管低頻渦帶引起的振動故障;A2為推力軸瓦不平引起的振動故障;A3為轉輪葉片開口不均引起的振動故障;A4為導葉開口不均引起的振動故障。

式中:S1(t)，S2(t)，S3(t)，S4(t)為含噪振動仿真信號;b1(t)，b2(t)，b3(t)，b4(t)為高斯白噪聲成分。S1(t)，S2(t)，S3(t)，S4(t)的振動波形,如圖2所示。應用改進EEMD對其進行10層分解，計算前9階IMF的標準差得到標準差曲線，如圖3所示。

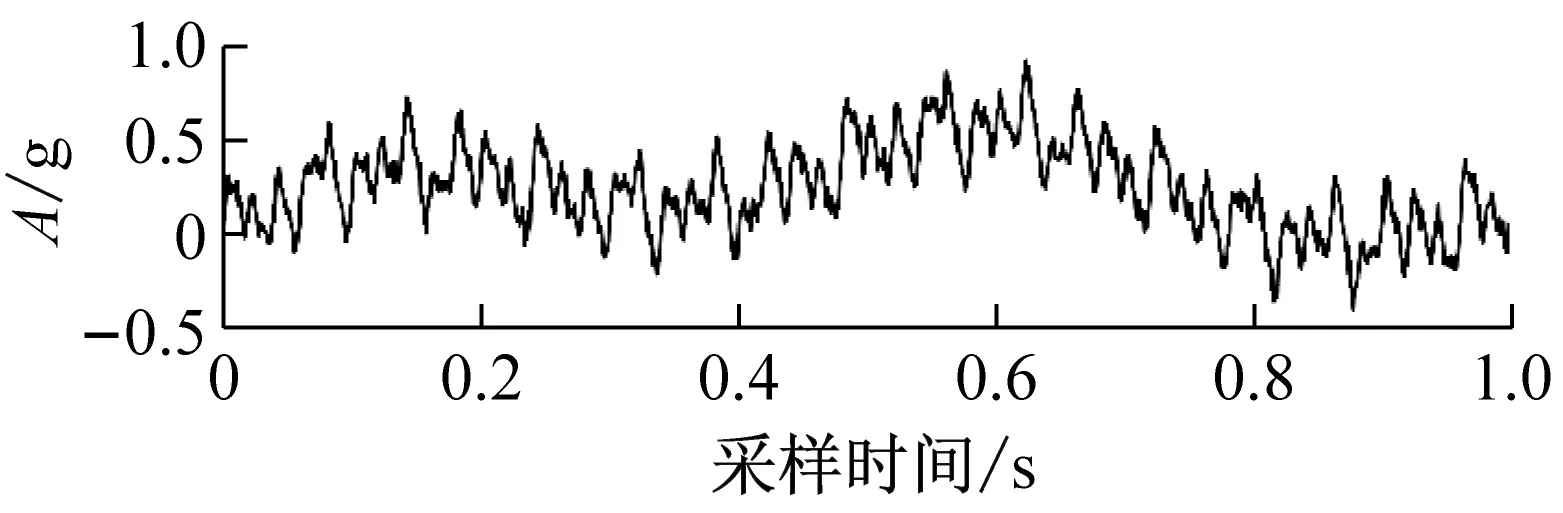
(a) 尾水管低頻渦帶引起的振動故障

從圖3可知，不同故障狀態振動信號各階IMF的標準差和其階數的關系存在明顯差異，可作為區分故障類別的特征參數。

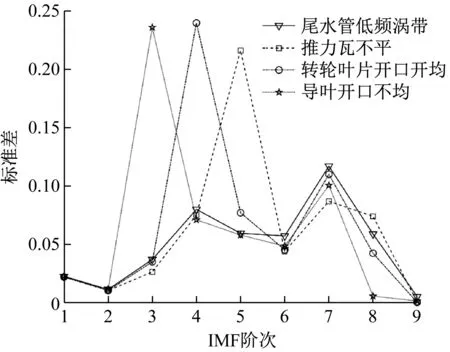
圖3 各階IMF標準差和其階數的關系曲線

2 隱馬爾科夫模型

隱馬爾科夫模型(HMM)是關于時序的概率模型，描述由一個隱藏的馬爾可夫鏈隨機生成不可觀測的狀態隨機序列I=(i1,i2,…,iT)，再由各個狀態生成一個觀測而產生觀測隨機序列O=(o1,o2,…,oT)的過程，序列的每一個位置又可以看作是一個時刻[14]。一個HMM通常由以下幾個參數來描述：

(1) 馬爾科夫鏈隱狀態數N。所有可能狀態的集合記為Q={q1,q2,…,qN}。

(2) 在各個隱狀態下所有可觀測值數M。所有可能觀測的集合記為V={v2,v2,…,vM}。

(3) 隱狀態間狀態轉移概率矩陣

A=[aij]N×N,

aij=P(it+1=qj|it=qi),

i=1,2,…,N;j=1,2,…,N

式中，aij為在時刻t處于狀態qi的條件下在時刻t+1轉移到狀態qj的概率。

(4) 觀測概率矩陣

B=[bj(k)]N×M,

bj(k)=P(ot=vk|it=qj),

k=1,2,…,M;j=1,2,…,N

式中，bj(k)為在時刻t處于狀態qj的條件下生成觀測vk的概率。

(5) 初始狀態概率分布矢量

πi=P(i1=qi),i=1,2,…,N

式中，πi為時刻t=1處于狀態qi的概率。λ=(A,B,π)被稱為隱馬爾科夫模型的三要素。

3 基于EEMD-SDCCⅠ-HMM的故障識別方法

3.1 HMM模型在故障識別中的應用

HMM應用于設備故障識別的方法可歸納為：首先，對訓練數據進行特征提取和標量量化，其次建立具有相應隱狀態數和觀測值數的HMM，然后利用該模型計算待測數據與訓練數據的相似概率，根據相似概率的差異判斷信號狀態的變化，最終實現模式分類。考慮實際應用需求，本文采用參數少，訓練快的離散型隱馬爾科夫模型(discrete hidden Markov model，DHMM)，其輸入的觀測值為離散值，需要對特征向量進行離散化處理，常用的離散化處理方法包括矢量量化和基于Lloyds算法的標量量化等[15-16]。在實際情況中，信號的幅值會因所處環境改變而發生變化，故IMF的標準差幅值也可能隨之改變。因此直接使用每個IMF標準差幅值的量化值作為故障特征是不合適的。而標準差曲線的變化趨勢包含了由故障機理所決定的信號內在特性，受信號幅值變化的影響很小，可利用編碼的方法對趨勢進行記憶并以此作為故障特征。基于以上分析，本文提出一種曲線趨勢編碼(curve trend coding,CC)方式用于將信號IMF分量標準差值離散化。

3.2 標準差曲線趨勢編碼

由有限點連接而成的曲線，如圖3中的標準差曲線，是由多個線段組成的。可以看出，線段有3種趨勢：上升、水平和下降。若使用不同的整數(如0，1，2)表示這3種趨勢，則按線段排列順序可得一串數字碼，稱為該曲線的線碼。假設使用0，1，2進行編碼，則能寫出總計6種不同的編碼方式，如表3所示。標準差曲線的每段由一個線碼位表示，可通過此方法計算得出圖3中標準差曲線相應的線碼。

表3 曲線趨勢的編碼方式

實際中，理想的水平趨勢幾乎不可能存在。為解決其編碼問題，本文引入趨勢裕度(trend margin，TM)公式中為MT，放寬水平趨勢的判定條件。假設對信號進行EEMD得到m個IMF，當采用編碼方式一時，編碼方式如圖4所示，具體過程如下：

圖4 編碼方式示意圖

(1) 計算標準差曲線最大值和最小值的差值Ad

Ad=max{DS1,…,DSm}-min{DS1,…,DSm}

(9)

(2) 由式(10)所示的判斷條件，確定各線碼位的值Ci

(10)

此處，MT為常數，由于MT過小時，無意義的平穩趨勢可能被判定為上升趨勢或下降趨勢;而MT過大時，有意義的上升或下降趨勢可能被判定為平穩趨勢。這兩種情況對于特征提取都是不利的，根據經驗MT值取0.05～0.20較好。

(3) 將各線碼位的值Ci按順序連接，如式(11)所示。

CC=C1C2…Cm-1

(11)

3.3 編碼方式分析

為選出最佳編碼方式，利用轉子正常、碰磨、不平衡和不對中共4種狀態的振動信號進行分析，降噪后的振動信號如圖5所示。

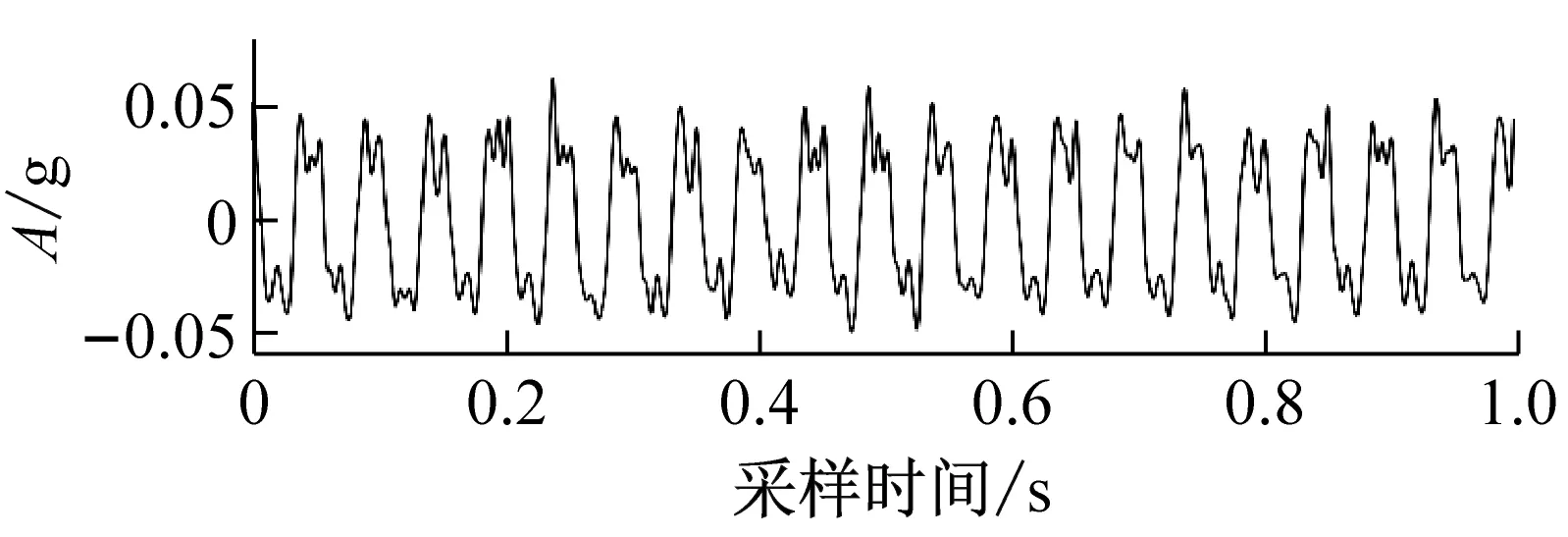
(a) 正常

采用EEMD對不同轉子狀態的振動信號進行10層分解。各狀態分解所得IMF,如圖6所示。可以看出，IMF的幅值隨其階數的增大呈現出先增大后減小的趨勢，其中，正常和碰磨信號的IMF最大幅值均出現在第5階IMF中，不平衡和不對中信號則出現在第4階IMF中。計算4種狀態各階IMF的標準差得到對應標準差曲線，圖7給出了每種轉子狀態下的10組IMF標準差曲線。

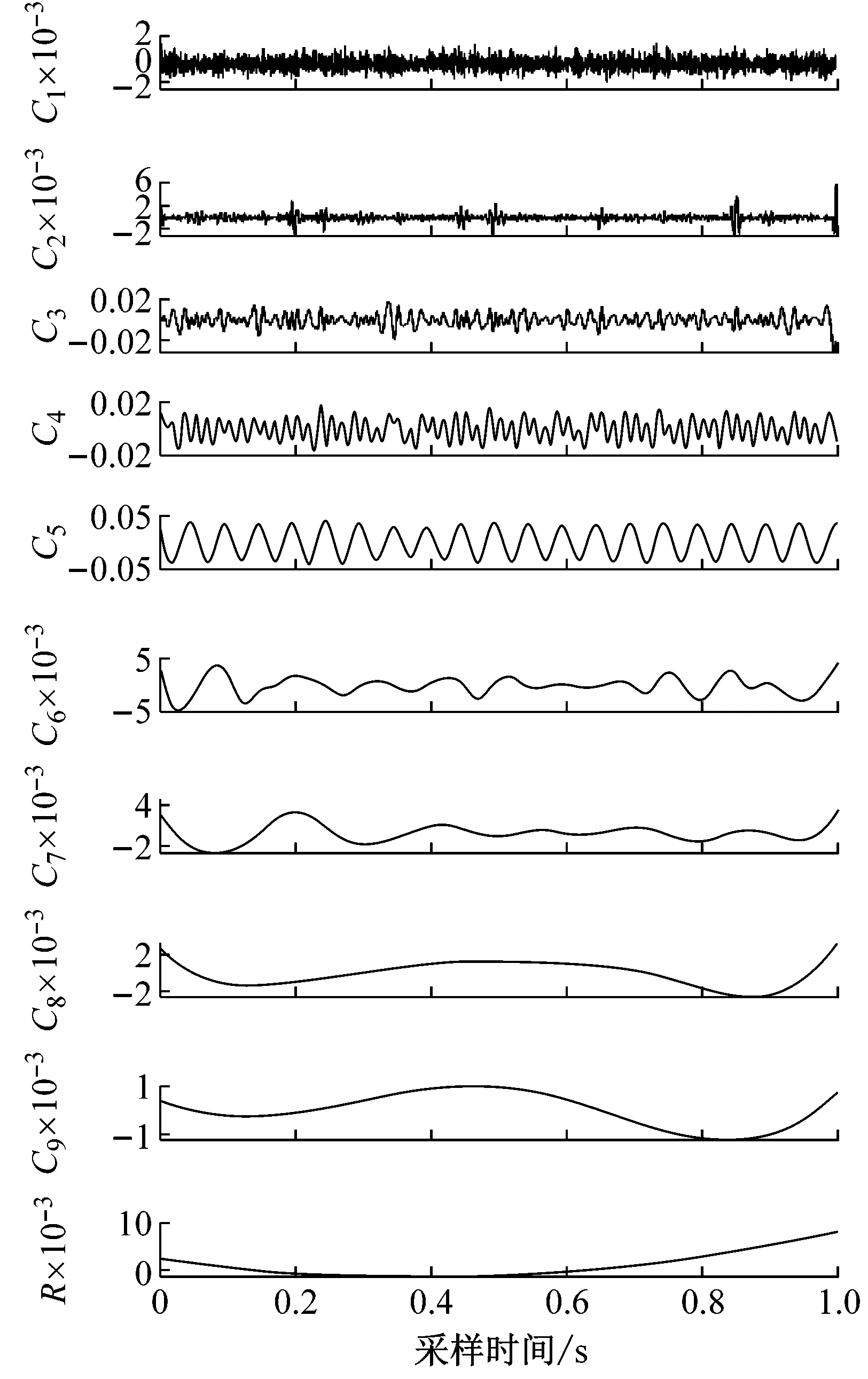
(a) 正常

由圖7可知，同一轉子狀態的IMF標準差曲線具有相似性，不同轉子狀態的IMF標準差曲線有較大差異。根據3.2節所述編碼方法，用表3中的6種編碼方式對圖7中4種轉子狀態對應的IMF標準差曲線進行編碼，結果如表4所示。

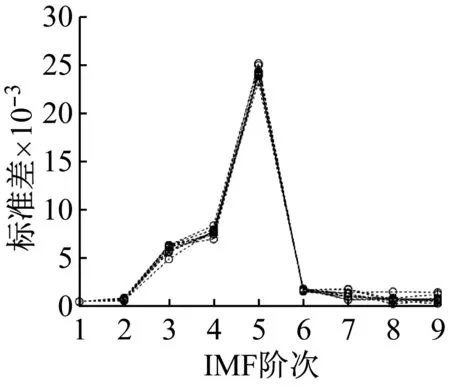
(a) 正常

表4 不同轉子狀態的IMF標準差曲線編碼

采用歐拉距離(d)來估計任意兩條曲線的相似程度，以確定最好的編碼方式，計算公式如式(12)所示。

(d) 不對中狀態測試樣本在各HMM上的輸出值

(12)

式中:m為IMF總數;Ci,k和Cj,k分別為樣本i和樣本j第k個線碼位的值。此處在確定各線碼位的值時，MT取0.1。圖8顯示了來源于轉子正常，碰磨和不對中狀態的3組振動信號IMF標準差曲線，圖9顯示了兩組待測樣本的IMF標準差曲線，分別來源于轉子碰磨和不對中狀態。各樣本的IMF標準差如表5所示。加粗的數據表示故障狀態與正常狀態曲線之間差別較大的部分。

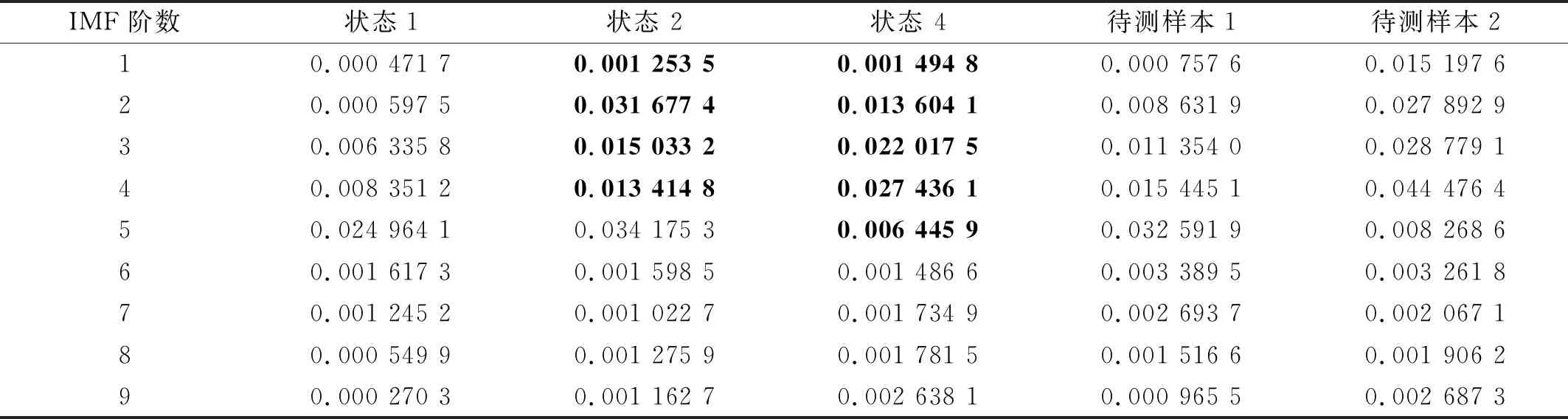
表5 圖8和圖9中振動信號各階IMF標準差

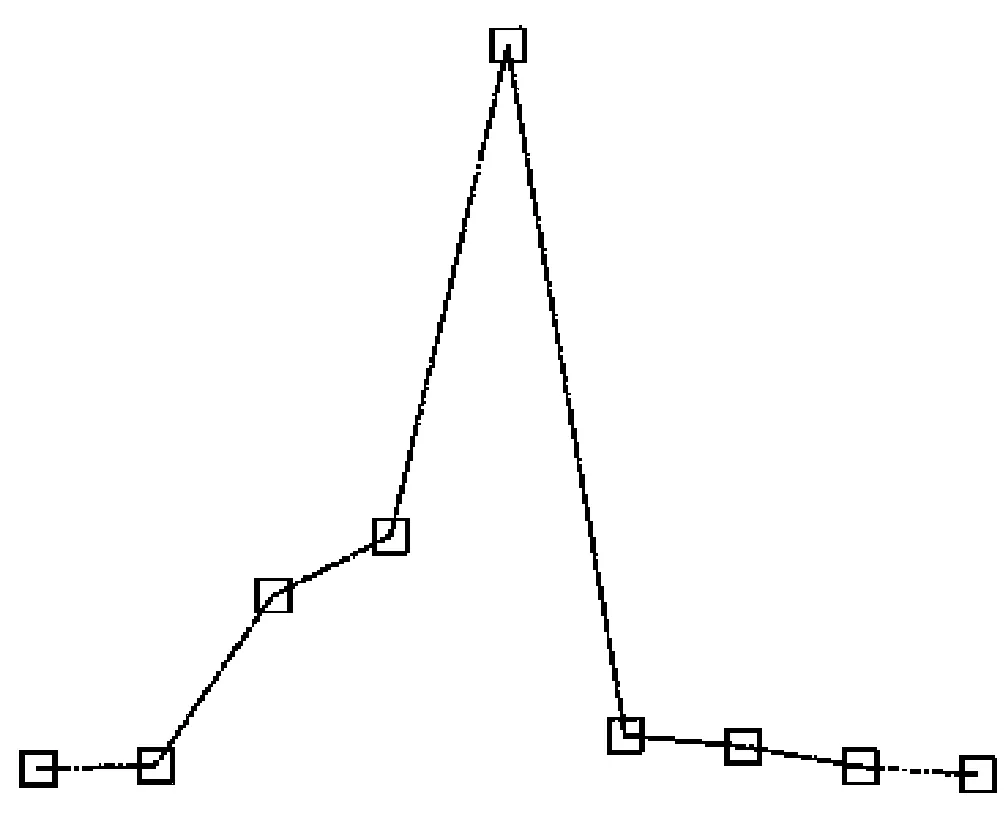
(a) 狀態1

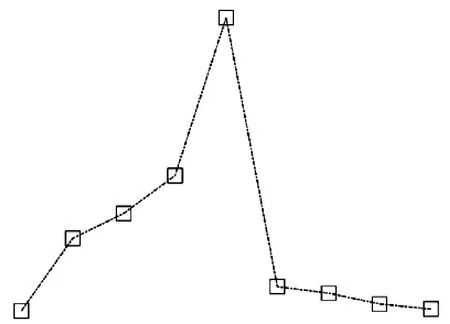
(a) 待測樣本1(屬于狀態2)

從表5、圖7和圖8可以看出，轉子碰磨和正常的明顯區別在于IMF標準差曲線的前3段，即第2～第4階IMF標準差。轉子不對中和正常的明顯區別在于IMF標準差曲線的前4段，即第2～第5階IMF標準差。而圖9中待測樣本與圖8中相同狀態樣本的標準差曲線也存在差異。由對稱性知，編碼方式一和六、編碼方式二和四、編碼方式三和五具有相同的效果，故利用表3中前3種編碼方式對圖8和圖9中信號的IMF標準差曲線進行編碼，并計算圖9中待測樣本與圖8中3種樣本的歐氏距離，結果如表6所示。

由表6可知:編碼方式一對于兩個待測樣本狀態的分類是正確的;而編碼方式二無法區分待測樣本1是碰磨還是不對中;編碼方式三將待測樣本1誤分類至正常和不對中。盡管3種編碼方式對待測樣本2的分類都是正確的，但從距離角度看，使用編碼方式二、三得到的關于待測樣本2和狀態4的線碼間距離要大于使用編碼方式一所得到的對應距離，這表明使用編碼方式一對轉子正常狀態和不對中故障的區分效果最好。

表6 圖8和圖9中不同IMF標準差曲線的編碼結果及距離

綜合以上實例可以得出結論：編碼方式一在所有編碼方式中對于轉子故障狀態識別效果最好。而從理論上分析，編碼方式一應為最理想的編碼方式，因為由編碼方式一得到曲線上升和下降趨勢的線碼位與平穩趨勢的線碼位數值之差即距離相等，編碼方式二和三的區別在于前者上升與平穩趨勢之間的距離大于下降與平穩趨勢之間的距離，后者則相反。因此，之后的分析均采用編碼方式一(curve codeⅠ,CCⅠ)對IMF標準差曲線進行編碼。

3.4 基于EEMD-SDCCⅠ-HMM的故障識別過程

綜合3.2節和3.3節關于IMF標準差曲線趨勢編碼方式的研究結果,結合HMM在故障識別中的優勢,本文提出了基于EEMD-SDCCⅠ-HMM(ensemble empirical mode decomposirion-standard deviation curve codeⅠ-hidden Markov model)的故障識別方法，圖10為利用EEMD-SDCCⅠ-HMM進行故障識別的流程，詳細說明如下。

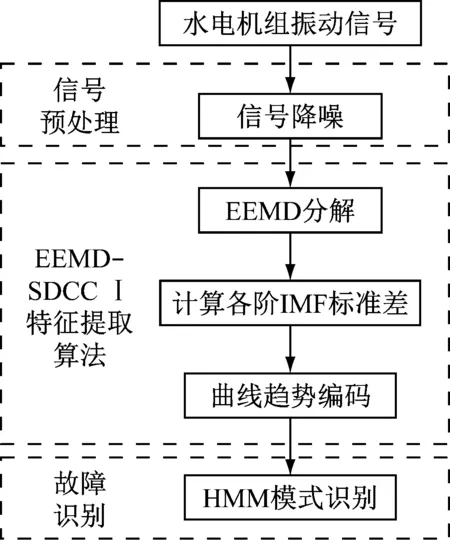
圖10 基于EEMD-SDCCⅠ-HMM的故障識別流程

(1) 信號預處理。由于測量環境和機械振動的影響，測量信號中存在較高能量的噪聲，為更加充分地提取故障信號中的有效信息，需要在信號分析前對帶噪聲信號進行一定程度的降噪處理。本文采用小波軟閾值降噪去除原始信號中的噪聲。

(2) 信號EEMD分解。對降噪后的信號進行EEMD分解得到IMF。

(3) 計算各階IMF的標準差并編碼。計算各階IMF的標準差，并用3.3節所述CCⅠ編碼方式對所有IMF標準差進行編碼，將各線碼位的值按順序連接構成特征向量。

(4) 將各狀態特征向量輸入HMM進行模式識別。將各狀態特征向量組成觀測序列輸入HMM，采用Baum-Welch算法訓練各狀態HMM[17]，得到模型參數λ=(A,B,π)。模型訓練結束后，對于未知狀態的數據，提取其特征向量后輸入到各HMM中，采用前向-后向算法計算特征向量在各模型下的對數似然概率值，輸出概率值最大的模型即為待測數據的原始模型。

4 試驗及驗證

為了驗證基于EEMD-SDCCⅠ-HMM的水電機組故障識別方法的有效性，分別采用轉子試驗臺模擬機組振動信號和水電機組實測振動信號進行試驗，并設計了對比試驗以說明所提方法的優越性。

4.1 轉子振動試驗臺故障識別(實例一)

圖11為本試驗所采用的轉子試驗臺系統，轉子直徑10 mm，長850 mm，安裝有兩個直徑75 mm的轉盤，兩段轉軸經聯軸器連接，由4個軸承支撐，另有兩個碰摩螺紋箱安裝在系統支架上。轉子由一臺直流電機驅動，用DH5600轉速控制器控制其轉速。轉子振動信號由傳感器采集后傳輸給前置器，進行放大和濾波，最后傳入計算機進行存儲、顯示和分析。利用該試驗臺分別模擬機組正常狀態和碰磨，不平衡，不對中3種機組常見故障。其中，碰摩故障通過將碰摩螺栓旋入碰摩螺紋箱中，使其與轉軸接觸實現；不平衡故障通過將2 g的質量塊旋入轉盤邊緣處的螺紋孔內實現；不對中故障則通過錯置聯軸器處兩軸的位置實現。

圖11 轉子試驗臺系統

采集信號時，設定機組轉速為1 200 r/min，采樣頻率為2 048 Hz。對4種機組狀態分別采集100組數據，每組數據包含2 048個點。4種機組狀態的振動信號如圖12所示。

(a) 正常

對各機組狀態振動信號進行預處理，降噪時選擇“db8”小波進行3層分解。由于試驗數據包含4種機組狀態，故需建立4個HMM，分別代表機組正常，碰磨，不平衡和不對中狀態。使用K-means聚類方法對經過EEMD-SDCCⅠ算法得到的特征向量聚類，以確定各HMM的隱狀態個數，K值由Calinski-Harabaz指數確定。Calinski-Harabaz指數是聚類模型的常見評價指標，其定義如式(13)所示

(13)

式中:N為數據集樣本數;k為簇類個數;tr(Bk)，Tr(Wk)分別為簇間散度矩陣和簇內散度矩陣的跡。Bk和Wk的計算公式如式(14)和式(15)所示。tr(Bk)為不同簇間的遠離程度，跡越大，不同簇間的遠離程度越大;tr(Wk)為同一簇類的密集程度，跡越小，同一簇類的數據集越密集。由以上定義可知，Calinski-Harabaz指數越高，聚類性能越好。

(14)

(15)

式中:nq為簇類q的樣本數;cq為簇類q的中心;c為所有數據集的中心;Cq為簇類q的樣本集。

經過試驗，確定機組正常，碰磨，不平衡和不對中的隱狀態個數分別為6，3，6，3。由于觀察矩陣的初值對模型性能影響較大，故在模型訓練時采用多次隨機初始化，選擇得分最高的參數作為模型最佳參數。將4種機組狀態前70組IMF標準差線碼構成的特征向量作為訓練數據，收斂誤差設定為1×10-3。4種狀態剩余30組IMF標準差線碼作為測試數據，輸入訓練好的各HMM中，得到各HMM輸出概率值P(O|λ)，如圖13所示。

從圖13可以看出，4種機組狀態測試樣本在各自對應的HMM模型輸出概率值最大，分類準確率達到100%，表明EEMD-SDCCⅠ-HMM故障識別模型能有效識別機組正常，碰磨，不平衡和不對中狀態，且識別準確率高。

為了對比驗證該模型的識別效果，分別采用不同方法對相同的樣本進行處理，比較識別結果，如表7所示。其中，編碼方式 CCⅡ(curve codeⅡ)表示采用Lloyds算法進行標量量化。VMD-SD-KNN(ariational mode decomposition-standard deviations-k-nearest neighbor)對信號采用VMD分解，分解層數為6層，將信號6階IMF分量標準差向量輸入k近鄰分類器(k-nearest neighbor，KNN)進行分類。WT-SampEn-KNN(wavelet transform-sample entropy-k-nearest neighbor)對信號采取小波變換，用MATLAB軟件的小波函數wavedec和wrcoef進行分解和重構,小波基函數選擇“db3”，分解層數為4層，得到一個小波近似系數和4個小波細節系數，計算各小波系數的樣本熵，作為特征向量輸入KNN進行分類。

表7 不同故障識別模型對比

將分類器分類類別與原始真實類別一一對應后，采用多分類準確率(P)和多分類召回率(R)評估模型性能。假定原始類別i對應的多分類器輸出為i，類別數為K，P和R的計算公式分別如式(16)和式(17)所示。

(16)

(17)

式中:ni為多分類輸出的類別為i的樣本數量;nii為真實類別為ci且被分類器分類至類別i的的樣本數量，即被正確分類的屬于類別i的樣本數量，njj同理。nij表示真實類別為ci卻被分類器分類至類別j的的樣本數量，i=1,2，…，K;j=1,2，…，K。為了平衡準確率與召回率的不同影響，采用多分類的F均值作為故障識別模型的綜合評價指標。F均值定義如式(18)所示

(18)

當α=1時，F均值又稱為準確率與召回率的調和均值，記作F1。

從表7可以看出，在訓練樣本集和測試樣本集相同的情況下，信號分解方法，IMF的特征參數，編碼方式和分類模型都會影響故障識別結果。在以上幾種故障識別模型中，本文提出的EEMD-SDCCⅠ-HMM模型故障識別效果最佳，達到了100%，即能完全準確地識別機組正常，碰磨，不平衡和不對中狀態。此外，對比特征提取所需時間可知， EEMD-SDCCⅠ-HMM模型耗時最短，因此也更有利于實現快速故障識別。

4.2 水電機組故障識別(實例二)

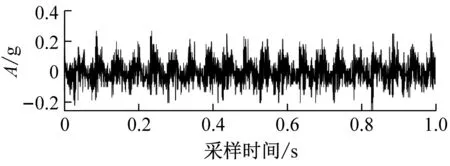
水電機組實測振動信號來源于S水電站的3號機組，水輪機型號為ZZA315-LJ-800，額定功率200 MW。巡檢人員發現該機組在運行過程中上機架、水車室、蝸殼以及尾水管等處有明顯異常聲音，停機檢查后發現機組轉輪室中環鋼板出現脫落，屬于水力不平衡故障。事后從電站在線監測系統中獲取機組正常運行和發生故障時的軸向振動數據，形成正常狀態和故障狀態樣本各40組，如圖14所示。

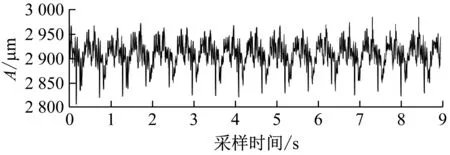
(a) 正常

各狀態前20組數據用于訓練，后20組用于測試。采用EEMD-StdCCⅠ計算水電機組實測振動信號的特征向量如表8所示。根據K-means聚類結果確定正常HMM的隱狀態數目為4，故障HMM的隱狀態數目為2。故障識別結果分別如圖15和表9所示。

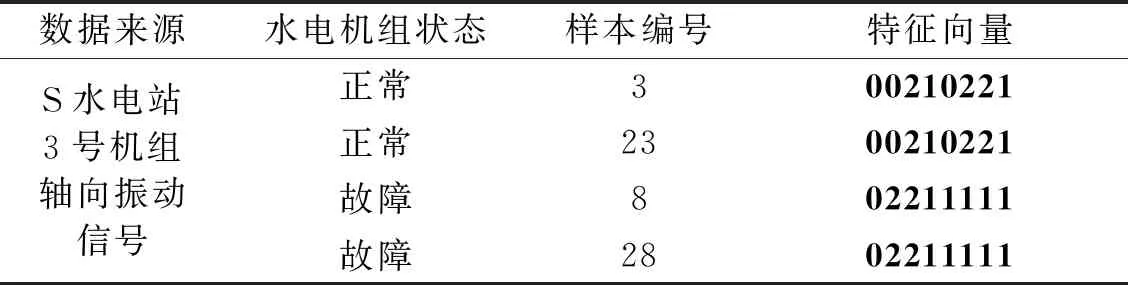
表8 水電機組實測振動信號特征向量

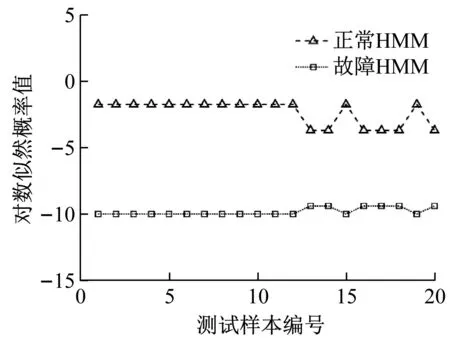
(a) 正常狀態測試樣本在各HMM上的輸出值

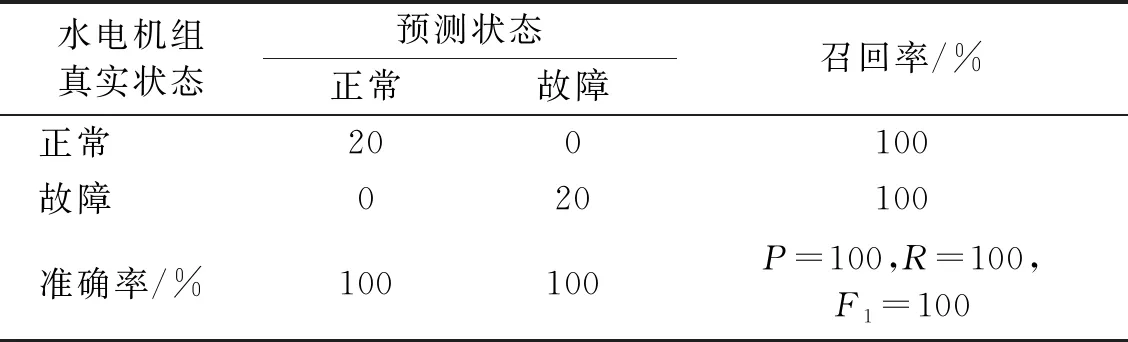
表9 EEMD-SDCCⅠ-HMM對水電機組的故障識別結果

從圖15和表9的故障識別結果可以看出，測試樣本的預測狀態與其真實狀態完全一致，表明基于EEMD-SDCCⅠ-HMM的故障識別方法對水電機組狀態具有良好的分類性能。

5 結 論

本文提出了基于EEMD和SDCCⅠ的水電機組振動信號特征提取新方法，對水電機組振動信號的IMF標準差特性及曲線編碼方式進行了分析，并給出了最佳編碼方式。同時，鑒于HMM在模式識別方面的優越性，將其引入水電機組振動故障診斷過程，建立不同機組狀態的HMM，實現了機組狀態的識別。最后用轉子振動信號和水電機組實測振動信號驗證了所提方法的有效性，試驗結果表明：

(1) 在不同機組狀態下采集的振動信號，對其進行EEMD分解后，所得IMF標準差曲線的趨勢特征存在差異，可作為機組狀態特征向量。

(2) 選擇CCⅠ編碼方式對IMF標準差曲線的趨勢進行編碼能夠提高狀態分類準確率。與其他方法相比，基于EEMD-SDCCⅠ特征提取算法耗時短，得到的特征向量具有穩定性和良好的區分性，結合HMM進行故障識別的準確率較高。

(3) EEMD-SDCCⅠ-HMM是一種有效的水電機組故障識別新方法。隨著大數據平臺相關技術日趨成熟，獲取水電機組故障數據的難度會逐漸降低，本文提出的基于EEMD-SDCCⅠ-HMM的故障識別方法具有敏感型強，模型訓練簡單的優勢，因此可以預見，該方法在水電機組故障診斷領域有很大應用潛力。