基于PSR-PCA-ANFIS模型的保定市中心城區水資源安全評價

張 彥，李明然，寇利卿

（河北省保定水文勘測研究中心，河北保定071000）

0 引言

水資源作為基礎的自然資源和戰略性經濟資源［1］，其安全問題與糧食安全、生態環境安全關系、經濟安全緊密相連，是國家生存和發展的戰略性問題［2］。隨著社會經濟的發展，水資源短缺、水生態惡化等水資源安全問題日趨嚴重，已成為社會關注的熱點問題。科學評價水資源安全對城市水資源合理開發利用和社會經濟的可持續發展具有十分重要現實意義。

目前，國內外學者對水資源安全的評價方法進行了大量研究。常見的方法有PSR 模型法［3］、層次分析法［4］、集對分析模型［5］、人工神經網絡法［6］、系統動力學法［7］、多層次多目標模糊優選法［8］、熵權及模糊物元模型法［9］、模糊綜合評價法［10］等。由于影響水資源安全的因素眾多，評價指標的選取目前還沒有統一標準，主觀性比較強，指標間信息的易重疊，而且選取的指標間具有復雜的非線性關系，單一的評價方法并不能很好地解決上述的問題，在綜合考慮以上影響因素后，本文嘗試以保定市中心城區為例，結合多種方法建立水資源安全評價標準，并對其水資源安全狀況進行綜合評價和分析，以期得出比較客觀的評價結果，為保定市中心城區的水資源的合理配置及其社會經濟的可持續發展提供科學的參考依據和技術支持，也為其他地區的水資源安全評價提供借鑒。

1 水資源安全評價指標體系的構建

1.1 基于壓力-狀態-響應模型的評價指標初選

壓力-狀態-響應（Pressure-State-Response，PSR）模型最初是由加拿大統計學家David J.Rapport 和Tony Friend 提出［11］，主要用于研究壓力、現狀與響應之間的關系。后經歐洲經濟合作與發展組織（OECD）對其修改后用于環境問題報告［12］。20世紀80年代末至90年代初，歐洲經濟合作與發展組織（OECD）和聯合國環境規劃署（UNEP）對其共同發展后用于環境問題框架體系研究［13］。

對水資源安全評價指標利用PSR 模型框架選取具有很好的邏輯性，人類的經濟活動、社會發展造成的水資源壓力作用于生態環境，生態環境承壓后又呈現出狀態的改變，進而影響人類通過政策、行為的變化對生態環境狀態的改變產生響應，如此往復循環，就形成了人類活動與生態環境之間的相互作用、相互制約的關系，即壓力-狀態-響應關系。依據此模型框架，借鑒相關水資源安全指標分級標準研究成果［1，3，14-18］，并結合保定市中心城區水資源特點和經濟社會發展實際狀況，遵循指標的代表性、科學性、可量化性，數據的易獲取性原則，從壓力、狀態、響應3 個方面選取24 個指標初步構建了保定市中心城區水資源安全綜合評價指標體系，同時根據指標對水資源安全的影響屬性，劃分為正向指標和負向指標，詳見表1。初選指標確立后，收集2009-2018年保定市中心城區相關數據，數據來源于《保定經濟統計年鑒》、《保定市水資源公報》以及保定市人民政府官方網站等。

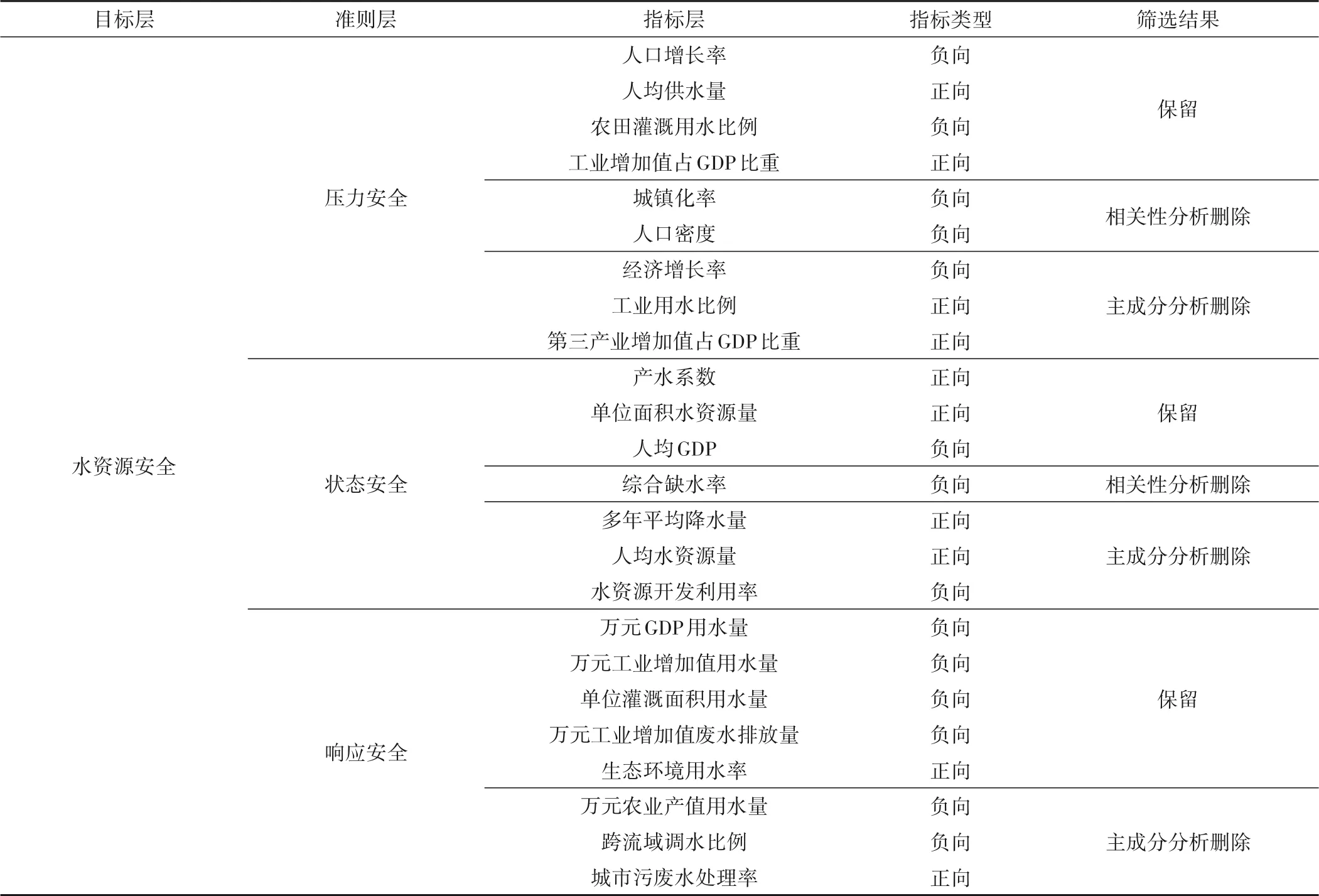
表1 水資源安全評價指標體系初選Tab.1 Primary selection of evaluation index system of water resources security

1.2 評價指標精簡

初步選取的評價指標間可能存在一定的相關性、冗余性，將對評價結果產生疊加的影響效應，因此需要對相關性顯著的指標進行約簡。本文采用相關性和主成分分析法結合的方法對初選指標進行精簡。

1.2.1 相關性分析指標篩選

應用IBM SPSS Statistics 24軟件，分別計算各準則層內的各指標間的皮爾遜相關系數，選出相關系數絕對值大于0.9［19］的指標進行分析取舍。

表2壓力指標準則層中的城鎮化率、人口密度、農田灌溉用水比例3個指標之間的相關系數絕對值均大于0.9，而農田灌溉用水比例更能直接反映農業活動的用水壓力，因此刪除與之相關的另外兩個指標。狀態指標準則層中人均水資源量和綜合缺水率兩個指標相關系數絕對值大于0.9，考慮到人均水資源量是國際常用的反映水資源量短缺狀態的指標，因此刪除綜合缺水率指標。最后，分別在表1 第5 列用“相關性分析刪除”標出。

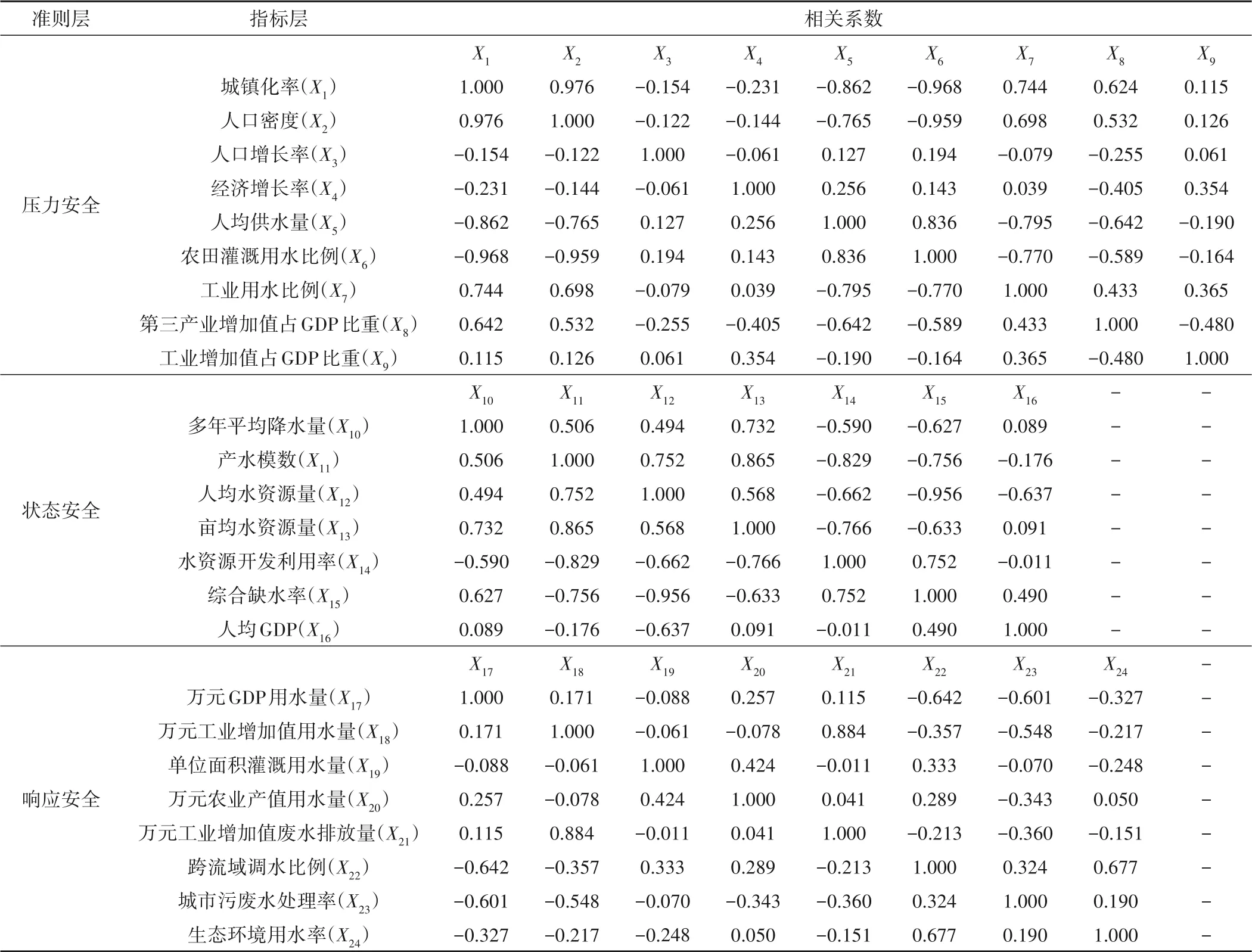
表2 準則層內指標間的相關性矩陣Tab.2 Correlation matrix among indicators in the criterion layer

1.2.2 主成分分析指標篩選

各準則層中指標經過相關性分析篩選之后，再應用主成分分析分別對各準則層中剩余指標再次篩選。主成分分析應用IBM SPSS Statistics 24軟件進行處理，主成分提取條件為初始特征值大于1，初始特征值方差累積百分比大于85%。指標選取的原則是：選取各準則層內的第一主成分的因子載荷系數絕對值大于0.9［19］的指標，以及其他提取的主成分因子載荷系數絕對值最大的指標。

依據以上原則，分別帶入各準則層中指標對應的數據進行主成分分析，各準則層主成分方差貢獻率結果見表3，主成分因子載荷系數表和主成分分析篩選結果見表4。

表3 主成分方差貢獻率 %Tab.3 Variance contribution rate of principal component

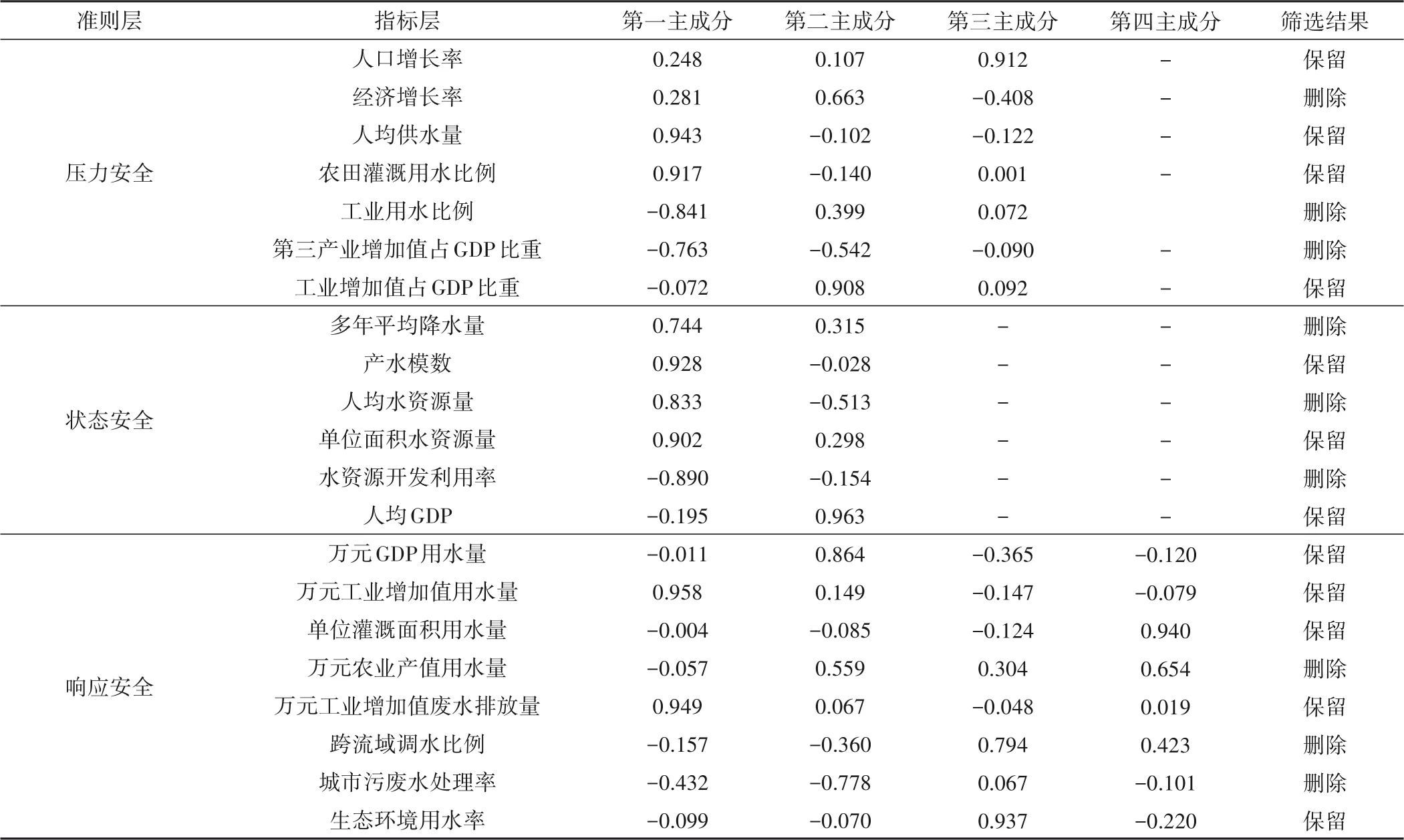
表4 主成分因子載荷系數Tab.4 Load coefficient of principal component factor

1.3 評價指標分級

各準則層內指標經過約簡后最終確定評價指標，對確定的指標需要制定水資源安全分級評價標準，依據優先選用國際、國內或地方水資源安全標準，其次參考相關研究成果、規劃目標，在沒有相關標準或文獻可供參考的情況尋求專家經驗值。依據以上原則，同時在結合本地區水資源特點、社會、人口和經濟發展的實際情況的基礎上，將保定市中心城區的水資源安全評價等級劃分為安全、較安全、臨界安全、不安全和極不安全5個等級，分別用1、2、3、4、5 表示，等級越高表示越不安全，具體的水資源安全分級標準范圍見表5。

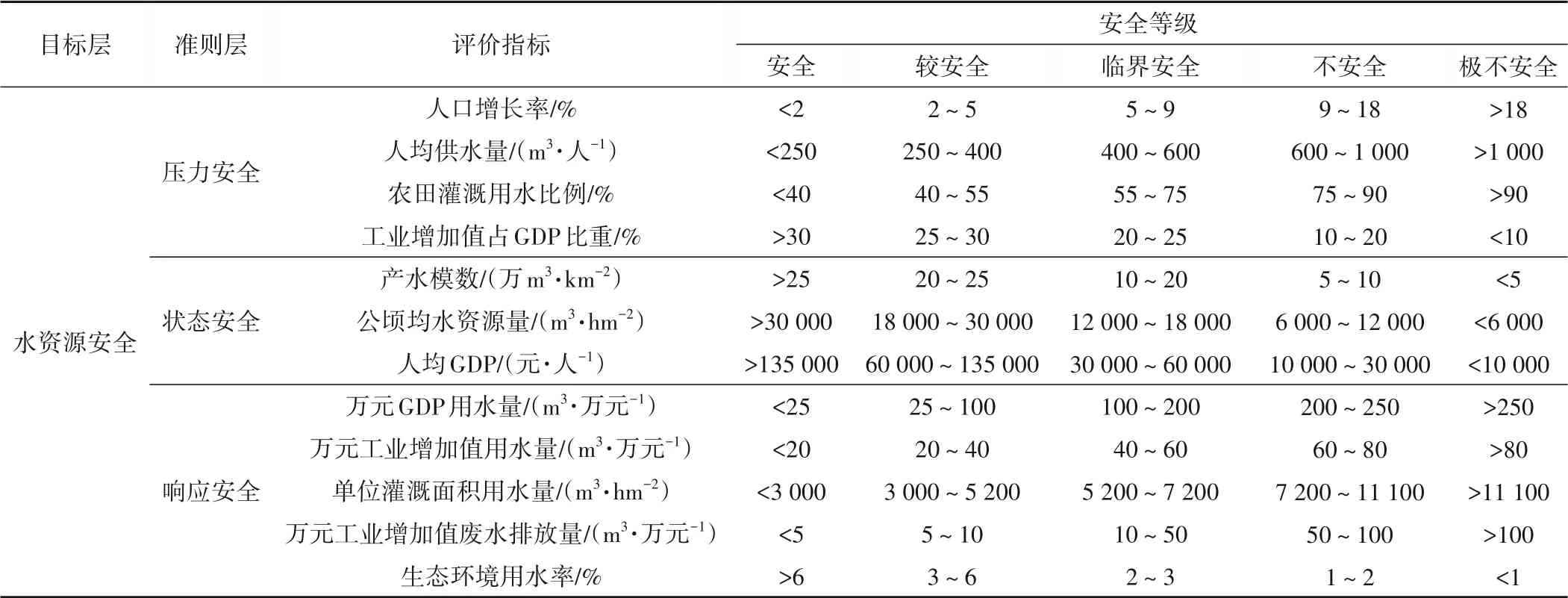
表5 水資源安全評價指標等級劃分標準Tab.5 Grading table for evaluation index of water resources security assessment

1.4 基于減法聚類的自適應模糊神經網絡評價模型的建立

1.4.1 減法聚類

減法聚類（Subtractive Clustering，SC）算法［20］是一種用來自動估計一組數據中的聚類個數以及位置的快速單次算法。該算法將每個數據點作為潛在的聚類中心，并計算其密度指標，然后將密度指標最大的點作為聚類中心，同時排除此數據點附近的數據成為聚類中心的可能；然后從剩下的可能作為聚類中心的數據中再找到最大的密度指標作為下一個聚類中心。依次循環，直到所有剩余數據作為聚類中心的可能性低于設定閾值。通過減法聚類算法可以確定模糊規則和輸入變量對應的隸屬度函數個數，并初始化前件參數。

由于最終確定的水資源安全評價指標較多，如果不預先合理劃分輸入空間，而采用網格分割方法劃分，將會產生大量的模糊規則，可能引起“組合爆炸”問題。而采用減法聚類，可以有效避免規則膨脹［21］，因此本文采用減法聚類來確定模糊系統的初始結構。

1.4.2 自適應模糊神經網絡模型網絡結構與算法

自適應模糊神經推理系統（Adaptive Neuro-Fuzzy Inference System，ANFIS）最初是在1993年由學者J.-S.R.Jang 提出的［22］。ANFIS 綜合了模糊規則的可解釋性和神經網絡自適應的優點，將神經網絡的自學習機制貫穿到模糊推理系統中，通過自動修正隸屬度函數的參數以及自動生成模糊規則等，使模糊推理系統具備了自學習、自適應的能力，極大地提高了這個系統應用范圍［23，34］。

本文的ANFIS 模型采用的是最常用的TaKagi-Sugeno（TS）型［25］模糊推理系統。假設一個具有兩條規則的簡單T-S型，x和y為兩個輸入變量，f為一個輸出變量，其對應的T-S 模糊推理模型是一階的，結構如下：

規則1：IfxisA1andyisB1thenf1=p1x+q1y+r1；

規則2：IfxisA2andyisB2thenf2=p2x+q2y+r2。

式中：Ai和Bi（i=1，2）是輸入變量對應的語言值模糊集；pi、qi、ri（i=1，2）為規則后件的線性參數。

與之相對應的ANFIS 模型網絡結構如圖1。ANFIS 模型從網絡結構上屬于多層前饋神經網絡，共分為五層，前四層稱為前件網絡，最后一層稱為后件網絡。設Oji為j層第i個節點的輸出值，各層介紹如下：

圖1 ANFIS模型網絡結構圖Fig.1 Network structure diagram of ANFIS model

第一層：輸入變量模糊化。本層將輸入變量模糊化，輸出對應模糊集的隸屬度。該層每個節點均為自適應節點。式中O1i表示第一層第i個輸出，μAi（x）、μBi-2（y）分別是輸入變量x、y所相對應的隸屬度函數。

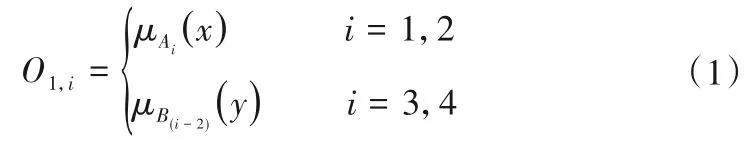
第二層：規則適應度的計算。該層每個節點輸出的是所輸入信號的積，結果為這條規則的適應度值，代表該條規則的激勵強度，用ωi表示。

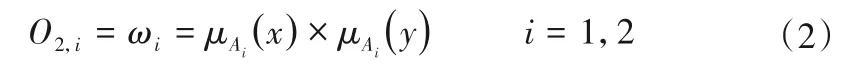
第三層：適應度的歸一化。對第二層得到的每條規則適應度進行歸一化處理。

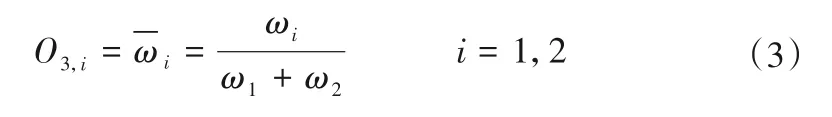
第四層：去模糊化處理。應用該層中每個節點中自帶的節點函數計算每條規則的輸出。

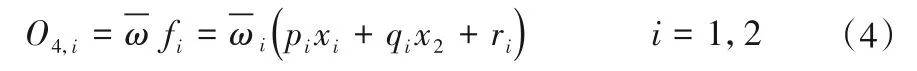
第五層：系統總輸出層。將上層計算得到的各條規則輸出的總和作為整個模糊系統的總輸出。

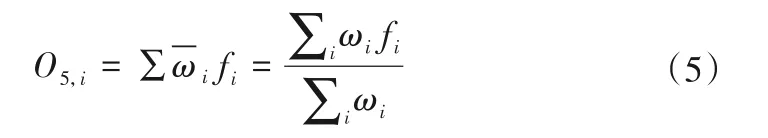
本文ANFIS 網絡結構中各層可調節的參數采用最小二乘估計法和反向傳播算法相結合的混合算法。其具體步驟是：首先輸入信號沿前件網絡正向傳遞直到第四層，固定前件參數不變，運用最小二乘估計算法更新規則后件參數；然后計算輸出層的結果與期望值的誤差，此時固定后件參數，將誤差信號由輸出層沿前件網絡反向傳播，用反向傳播算法更新前件參數，重復上述過程，直至滿足設定的誤差指標要求，迭代終止。

1.4.3 水資源安全評價模型的建立和訓練

Matlab（R2016a）軟件中提供了模糊邏輯工具箱，本文的ANFIS 建模和仿真都是應用工具箱中提供的圖形化編輯工具完成。

輸入、輸出的確定。評價指標最終精簡為12 項，因此AN?FIS 模型的輸入項為12 項，與之對應的水資源安全等級作為輸出項，用1，2，3，4，5 分別代表水資源安全的5 個級別，即輸出項為1 項。為了實驗樣本充足并具有普遍適用性，本文用unifrnd函數在評價指標相應級別之間進行隨機插值，每個分級區間隨機生成200個樣本，共生成1 000組的典型的輸入樣本。將水資源安全等級作為理論輸出值，因此共生成1 000 個輸出樣本。隨機抽取700 組數據作為訓練樣本，剩余300 組數據作為驗證樣本。應用mapminmax 函數將訓練樣本和驗證樣本歸一化到［-1，1］。

初始化模糊推理模型。輸入Anfisedit命令函數調出圖形編輯界面，導入訓練集。選用減法聚類法進行模糊區間劃分時，需要對Range of influence、Squash factor、Accept ratio 和Reject ratio 這4 個參數進行初始設置，由于前兩個參數對訓練誤差影響顯著［26］，因此本文只對前兩個參數組合進行參數尋優，后兩個參數采用系統默認值，經過多次訓練，最終確定Range of influence 設置為0.4，Squash factor 設置為0.45，Accept ratio 設置為0.5，Reject ratio 設置為0.15，得到聚類數為29個，模糊規則為29條，隸屬度函數選擇常用的高斯函數。

ANFIS 模型訓練與檢驗。訓練算法選擇hybrid 混合算法，為了防止過度擬合，允許誤差設定為0.001，訓練步數設定為200 步。經過訓練134 次，訓練誤差達到設定閾值，訓練終止，訓練誤差變化曲線見圖2。模型訓練完成后，導入驗證樣本進行網絡預測性能的驗證。ANFIS模型網絡擬合值和目標值對比見圖3，最終驗證誤差為0.007，說明99.3%驗證輸出與期望輸出吻合，由此可以證明此模型的泛化能力很強，用其進行水資源安全評價是實用有效的。

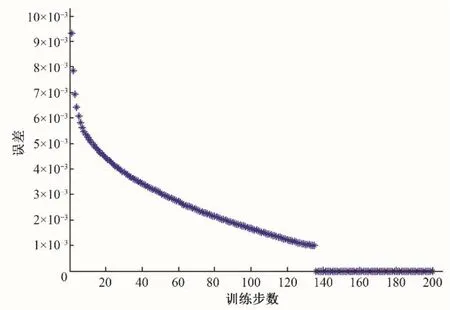
圖2 訓練誤差變化曲線圖Fig.2 The variation curve of training error

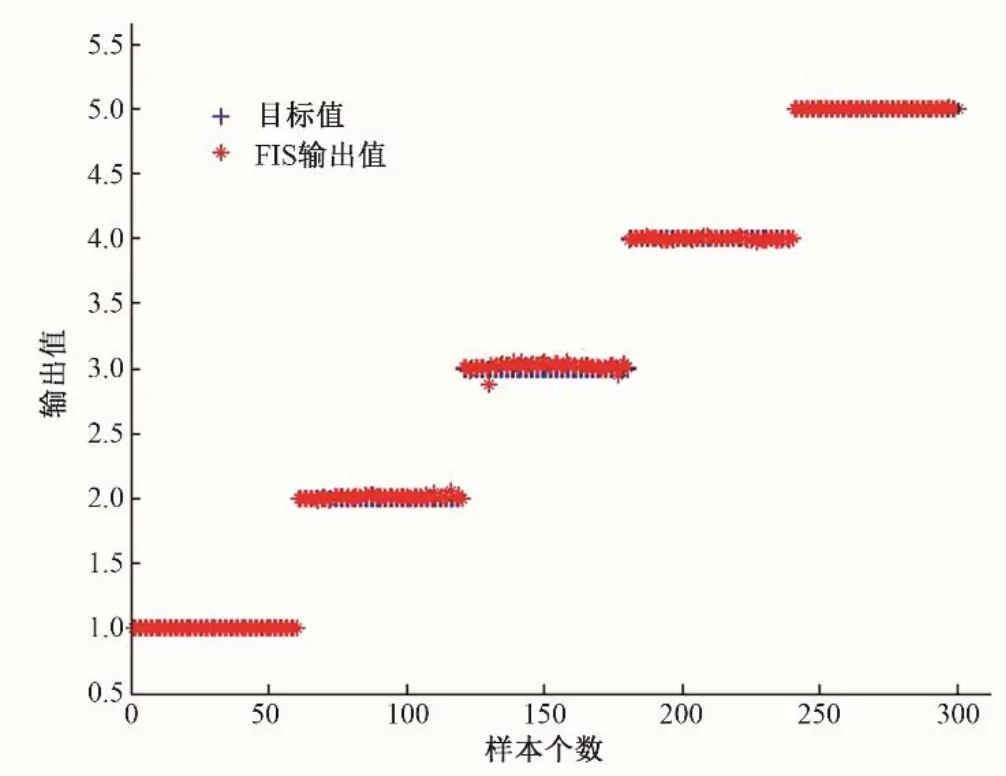
圖3 ANFIS模型擬合值和目標值對比圖Fig.3 Comparison of ANFIS model fitting value and target value

2 實例分析

2.1 研究區域概況

保定市位于河北省中部地區，與北京、天津成三角之勢，素有“京畿重地”、“都南屏翰”之稱，是國家歷史文化名城、國家園林城市，也是京津冀地區中心城市之一。本次所研究區域為保定市的中心城區，2015年4月，中心城區進行了區劃調整，在原來的主城區的基礎上將周邊的滿城縣、清苑縣、徐水縣撤縣建區并入其中，中心城區面積由原來的312 km2增加到2 531 km2，人口由119.4 萬人增加到280.6 萬人。中心城區的規劃調整，拓展了城市的發展空間，增強了城市的承載能力，有利于更好地承接首都功能疏解和產業轉移。但與此同時，由于中心城區水資源極度匱乏，水資源供需矛盾十分突出，水資源安全面臨巨大的挑戰。因此，開展保定市中心城區的水資源安全評價研究具有十分重要的現實意義。研究區概況圖見圖4。

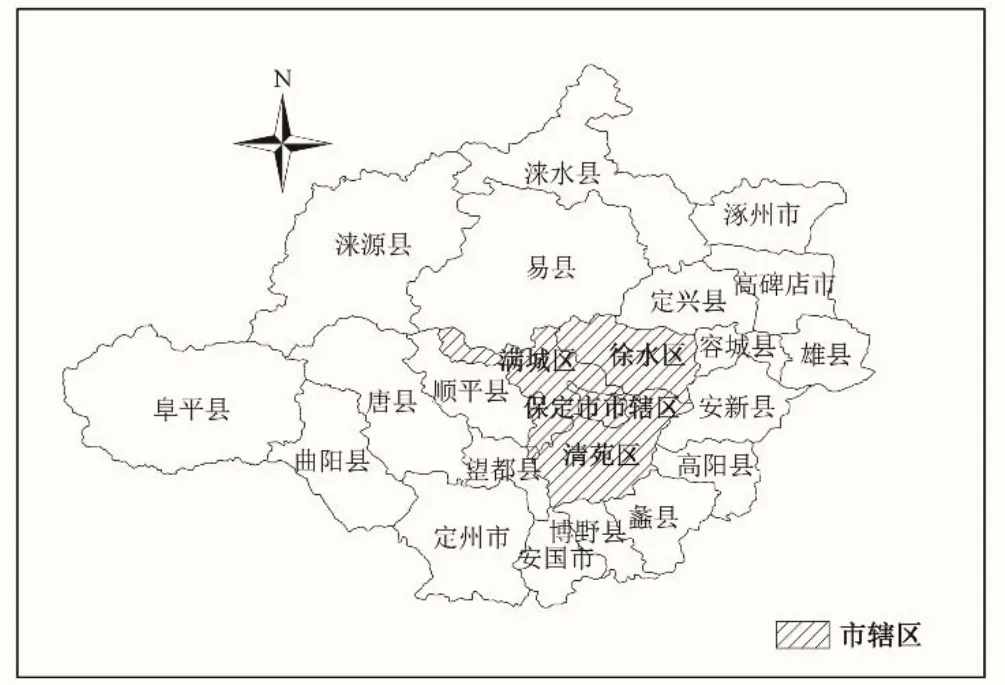
圖4 研究區域概況圖Fig.4 Overview of the study area

2.2 結果評價與分析

2.2.1 水資源安全綜合評價

將保定市中心城區2009-2018年各評價指標值應用map?minmax函數進行歸一化處理，再將歸一化后的值帶入到保存的ANFIS網絡里進行計算，對得到的輸出結果反歸一化，可得到保定市中心城區2009-2018年的水資源安全綜合評價等級，評價結果見圖5。由圖5 可知，保定市中心城區的水資源安全等級無明顯的變化趨勢，其中主城區水資源安全等級2009年和2014年為臨界安全，其余年份均為較安全，滿城區和徐水區除2017年安全等級為較安全外，其余年份均處在臨界安全，而清苑區一直處于臨界安全等級。綜上所述，2009-2018年期間，保定市中心城區水資源安全狀況無明顯變化趨勢，除主城區處于較安全外，其他區的水資源安全狀況主要處于臨界安全狀態，形勢不容樂觀。

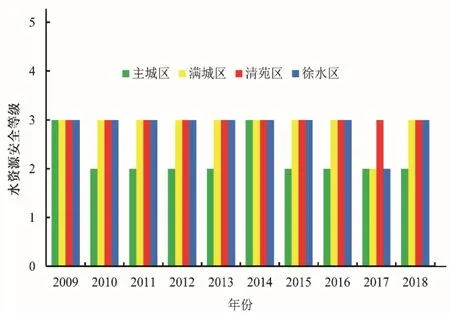
圖5 2009-2018年保定市中心城區水資源安全等級Fig.5 Water resource security level of Baoding central city from 2009 to 2018

2.2.2 水資源PSR安全綜合評價

參照保定市中心城區水資源安全綜合評價模型的建立和訓練方法，分別建立保定市中心城區的水資源壓力安全、狀態安全、響應安全的綜合評價模型，將2009-2018年3 個準則層的指標數據帶入各自訓練好的ANFIS 網絡，最終分別得出保定市中心城區的水資源壓力安全、狀態安全、響應安全綜合等級，見圖6～8。

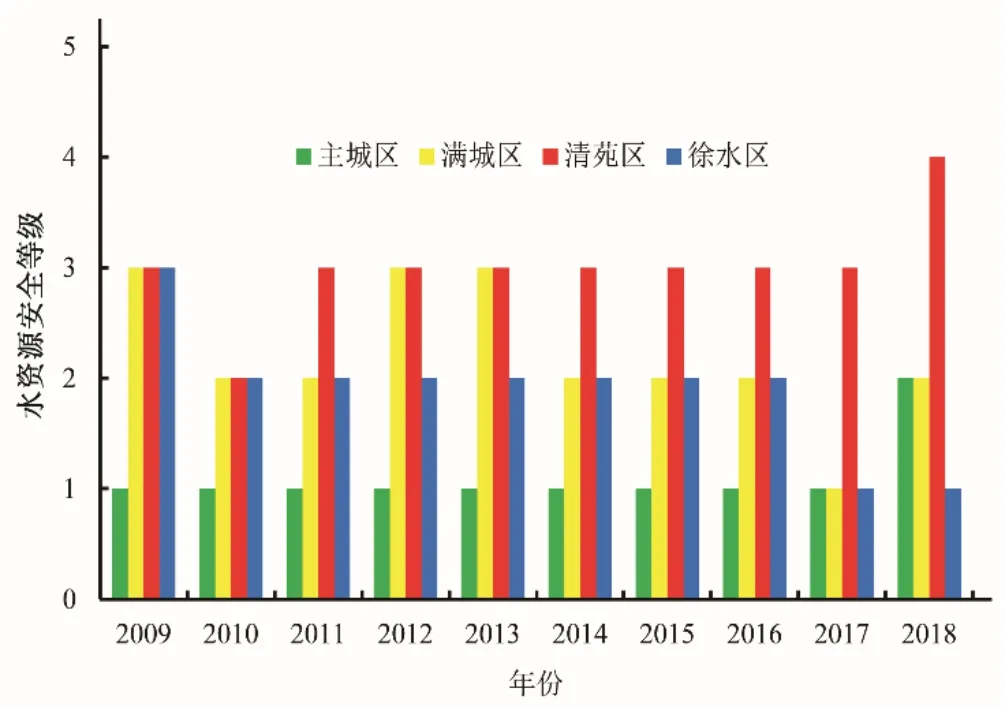
圖6 2009-2018年保定市中心城區水資源壓力安全等級Fig.6 The security level of water resource pressure in Baoding central city from 2009 to 2018

由圖6可知，2009-2018年保定市中心城區的4個區的壓力安全情況不盡相同，其中主城區的壓力安全情況良好，除2018年為較安全外，其他年份壓力安全等級均為安全；滿城區壓力安全情況相對較好，除2009年、2012-2013年為臨界安全外，其他年份壓力安全等級保持在較安全及以下；清苑區壓力安全情況不容樂觀，2009-2017年中除2010年壓力安全等級為較安全外，其他年份均為臨界安全，2018年為不安全，需要引起高度重視；徐水區的壓力安全等級由2009年的臨界安全轉為2017-2018年的安全。

由圖7 可知，2009-2018年保定市中心城區狀態安全情況比較嚴峻，其中主城區除2012年狀態安全等級為臨界安全外，其他年份均為不安全或極不安全；滿城區、清苑區和徐水區狀態安全等級均為不安全或極不安全。這與評價區域的水資源量匱乏，水資源供需矛盾突出的實際現狀相符合。

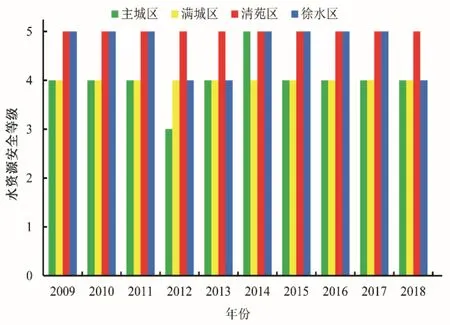
圖7 2009-2018年保定市中心城區水資源狀態安全等級Fig.7 The security level of water resource status in Baoding central city from 2009 to 2018

由圖8可知，2009-2018年保定市中心城區的4個區水資源的響應安全等級均有不同程度的好轉，其中主城區響應安全等級由較安全轉為2016-2018年的安全；滿城區由臨界安全轉為2013-2018年的較安全（2017年為臨界安全）；清苑區由臨界安全轉為2013-2018年的較安全；徐水區由臨界安全等級轉為2014-2018年的較安全（2015年為臨界安全）。

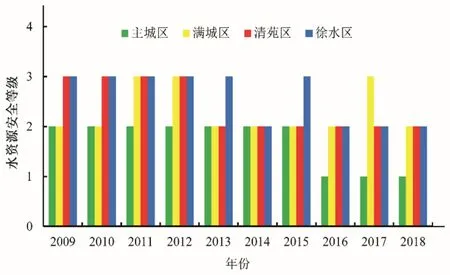
圖8 2009-2018年保定市中心城區水資源響應安全等級Fig.8 The security level of water resource response in Baoding central city from 2009 to 2018

綜上所述，在2009-2018年期間，水資源的狀態安全是影響保定市中心城區水資源安全的最主要因素。保定市清苑區水資源的壓力安全等級處于臨界安全或不安全狀態，其他區壓力安全狀況較好，中心城區水資源的狀態安全等級多處于不安全或極不安全狀況，中心城區水資源的響應安全狀況較好，均有好轉趨勢。

3 結論與討論

（1）PSR 模型為分析城市社會經濟發展和水資源之間相互影響構建了一個框架。基于PSR 模型框架并結合相關性分析和主成分分析所精簡的評價指標更加準確、有代表性，所建立的評價指標體系具有科學性和可行性。應用基于ANFIS 的水資源安全評價模型，建模方便，方法有效，評價結果客觀、易懂。

（2）從水資源安全綜合評價結果得出，2009-2018年保定市中心城區水資源安全狀況無明顯變化趨勢，除主城區處于較安全狀態外，其他區的水資源安全狀況主要處于臨界安全狀態，形勢不容樂觀。

（3）從水資源PSR 安全綜合評價結果得出，水資源的狀態安全是影響保定市中心城區水資源安全的最主要因素。保定市清苑區的水資源壓力安全狀況處于臨界安全或不安全狀態，其他區壓力安全狀況較好，中心城區水資源狀態安全狀況多處于不安全或極不安全狀態，中心城區水資源響應安全狀況較好，均有好轉趨勢。

（4）本文對水資源安全評價采用的是量化分級標準，其對評價結果至關重要，而目前尚未有統一的評價標準，因此，合理確定評價指標分級標準仍需繼續深入研究；在ANFIS 評價模型中，減法聚類的4個參數的設置、隸屬度函數的類型選擇和訓練次數的設定都會影響模型訓練和預測的精度，因此，在構建ANFIS模型時，對上述參數的設置的優化組合有待進一步研究。□