SCR脫硝系統的分數階PIλDμ參數優化控制

黃 宇， 高 珊， 李其賢， 丁 鵬， 王東風， 申朋宇

(1．華北電力大學 自動化系，河北保定 071003；2．保定電力職業技術學院 動力工程系，河北保定 071051)

據統計，煤炭燃燒是造成氮氧化物排放的主要原因。我國電力工業仍以燃煤為主，燃煤電廠是氮氧化物的主要排放源之一。NOx排放會形成酸雨，在陽光輻射的條件下與其他污染物發生反應，產生對人類健康有害的光化學煙霧。隨著環保法規的日趨嚴格以及人們環保意識的不斷增強，控制燃煤電廠的NOx排放成為一個亟須解決的問題。

目前，選擇性催化還原(SCR)脫硝技術是我國燃煤電廠控制NOx排放應用最廣、效果最好的方法之一，可以達到較高的脫硝效率，而且對工業條件的要求也很低。在SCR脫硝過程中，通常使用常規的比例積分微分(PID)控制策略，然而SCR脫硝系統存在較強的擾動特性和未建模動態特性，使得傳統PID控制器難以精確控制SCR脫硝系統。牛玉廣等[1]對SCR脫硝控制系統進行改進和優化。周洪煜等[2-3]利用神經網絡建立SCR脫硝系統數據模型，實現了系統噴氨量的最優控制。馬增輝等[4]在魯棒PID控制器的基礎上，利用魯棒時滯濾波器提高了SCR脫硝系統的抗干擾能力。秦天牧等[5]利用自適應智能前饋控制方法，實現了噴氨量的準確、及時調節。羅志浩等[6]將改進的動態矩陣控制(DMC)算法用于脫硝控制系統，該算法具有良好的響應特性，有效提高了系統的抗干擾能力。上述控制策略的研究方向各異，大部分能夠實現脫硝優化控制，使控制品質有一定程度的提升，但有些控制算法十分復雜，應用到工業生產的案例有限。為此，筆者在不改變原有脫硝控制系統組態的基礎上，將分數階PIλDμ(其中λ為積分階次，μ為微分階次)控制引入到SCR脫硝系統，以期解決SCR脫硝系統的控制問題。

分數階PIλDμ控制器由Podlubny[7]提出。目前的應用成果表明，分數階PIλDμ控制對外部擾動不敏感，能有效地提高系統的抗干擾能力及其動態特性。Alimohammadi等[8]將分數階PIλDμ控制應用到磁懸浮系統的內回路控制中，有效提高了其抗干擾性。戚壯等[9]將分數階PIλDμ控制應用到輕軌車輛的邊驅傳動系統，有效提高了受控輪對的抗軌道不平順激擾能力。王曉寸等[10]在逆變電源中加入分數階PIλDμ控制，極大改善了系統的動態性能，提高了其抗干擾能力。以上應用系統中均存在較強的擾動特性，分數階PIλDμ控制器的引入使系統具有較好的控制效果。由此，針對SCR脫硝系統存在的強擾動特性，筆者提出將分數階PIλDμ控制引入SCR脫硝控制系統,但是分數階PIλDμ控制器參數較多，在獲得較好控制效果的同時也提高了控制器參數的優化整定難度。

1 SCR脫硝控制系統動態分析

SCR脫硝是指在催化劑的作用下，還原劑與煙氣中的NOx發生反應，生成無毒無污染的N2和H2O。在上述化學反應過程中，由于噴氨量難以控制，無法有效脫除煙氣中的NOx，會造成機組設備損壞。因此，在保證脫硝效率的情況下，需要設計精準的SCR噴氨控制系統。

1.1 傳統SCR脫硝控制存在的問題

在工程應用中，SCR脫硝系統普遍采用串級PID控制，實現脫硝噴氨自動控制的方式主要有固定摩爾比控制、固定出口濃度控制和復合控制3種。固定摩爾比控制由于僅關注脫硝效率，沒有考慮出口NOx質量濃度變化，容易造成過度脫硝的現象；固定出口濃度控制側重考慮出口NOx質量濃度變化，容易導致噴氨過量，對環境造成污染；復合控制綜合考慮脫硝效率和催化劑脫硝能力，不僅能夠防止SCR脫硝系統出口NOx質量濃度超標，還能確保氨的逃逸率不超標[15]。雖然復合控制相對于前2種方式的控制效果較好，但由于受到火電機組的燃燒工況變化、氨濃度變化和催化劑活性等影響，系統呈現出較強的擾動特性，常規PID控制難以達到精準的控制效果。

為解決上述控制方式存在的問題，實現SCR脫硝系統出口NOx質量濃度的準確控制，在不改變原有控制系統結構的基礎上，提出一種基于復合控制方式的分數階PIλDμ控制策略。

1.2 SCR脫硝系統的分數階PIλDμ控制

SCR脫硝控制系統采用串級系統結構[16]。主回路采用分數階PIλDμ控制，控制器根據脫硝入口煙氣中NOx質量濃度的設定值與測量值之間的偏差修正所需的氨氣流量；副回路首先通過主回路分數階PIλDμ控制器修正的噴氨量和前饋回路的噴氨量共同作用得出設定噴氨量，然后采用傳統PID控制器計算噴氨量設定值與實測氨氣流量的差值，調整噴氨閥門開度以實現氨氣流量的控制。基于分數階PIλDμ控制的SCR脫硝系統結構框圖如圖1所示，其中f為函數,e為誤差。f函數的作用是將入口NOx質量濃度與煙氣流量相乘得到NOx質量流量。NOx質量流量乘以固定氨氮摩爾比得到SCR反應器入口的氨氣流量。f函數的數學表達式如式(1)所示。干擾信號d包含火電機組燃燒工況的改變、催化劑活性等干擾。

f=q×ρ

(1)

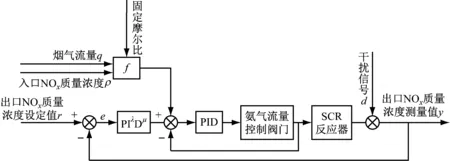
圖1 SCR脫硝分數階PIλDμ控制系統結構框圖

圖1中，氨氣流量對出口NOx質量濃度的傳遞函數Ga(s)[17]為：

(2)

控制閥門開度對氨氣流量的傳遞函數Gb(s)[18]為：

(3)

由于SCR脫硝系統中存在較多的擾動，如入口NOx質量濃度的改變、氨濃度變化引起系統噴氨量的變化以及脫硝反應的副反應產物引起催化劑活性的改變等。以上干擾都會對SCR脫硝系統的控制效果產生不良影響，因此將分數階PIλDμ控制器引入到SCR串級控制系統，可以克服上述不確定性干擾的影響。

2 分數階PIλDμ控制方案

相比傳統PID控制，分數階PIλDμ控制器具有更廣的控制范圍，可以通過改變分數階次的系數，在滿足系統穩定性的同時實現較強的系統控制能力。分數階PIλDμ控制器的傳遞函數Gc(s)為：

(4)

式中：λ≥0；μ≥0；KP為比例增益；KI為積分系數；KD為微分系數。

顯然，當λ和μ都為1時，式(4)為傳統PID控制。傳統PID控制器積分環節的作用是提高系統穩定精度，但會導致系統相角出現90°滯后的現象；微分環節可以改善系統的動態性能，但對系統的抗干擾性有一定的影響。分數階PIλDμ控制器可以通過調節積分階次，適當考慮系統的滯后相角，改善系統的動態性能；分數階PIλDμ控制器也可以通過改變微分階次,更加靈活地調節系統的阻尼程度，提高系統的抗干擾能力。

3 帶CMA-ES采樣器Optuna優化算法

3.1 Optuna

Optuna是由日本深度學習公司Perferred Networks提出的一種自動化超參數/參數優化框架，其定義只有3個核心的概念，即目標函數、單次試驗和研究[14]。在優化過程中，Optuna通過反復調用并評估不同參數值的目標函數獲取最優解。

Optuna優化算法的具體流程如下：(1) 初始化,確定優化方向、參數類型、取值范圍和最大迭代次數；(2) 進入循環；(3) 在定義參數取值范圍的目標函數內均勻選擇種群個體；(4) 修剪器按修剪條件自動終止毫無希望的種群個體；(5) 計算未被修剪的種群個體目標函數值；(6) 重復以上步驟，直到達到最大迭代次數，跳出循環；(7) 輸出最優解及最優目標函數值。

從上述流程中可以看出，首先通過創建一個研究框架，指定優化方向和迭代次數等，然后調用目標函數，單次試驗在定義參數取值范圍的目標函數內均勻選擇種群個體，然而此獲取參數的方式極大降低了Optuna的收斂速度，影響其優化效率。因此，筆者將CMA-ES的采樣原理引入Optuna，以提高參數優化性能。

3.2 CMA-ES算法

CMA-ES算法是由Hansen[19]提出的優化算法，利用高斯分布采樣優化問題的解空間，使用其中較好的解對高斯分布的參數進行更新，在滿足停止條件之前，不斷重復采樣和更新的過程。CMA-ES算法的具體步驟如下：

(1) 采樣新解。CMA-ES算法在待優化問題的解空間中隨機選擇一個解，然后根據正態分布生成的種群如下：

(5)

式中：xi為種群中第i個個體；α為種群大小；g為進化代數；m為搜索分布的均值；σ為步長；C為種群的協方差自適應矩陣，初始的C可以設置為一個D×D的單位矩陣，其中D為解的維度。

(2) 更新均值。在生成的種群中選擇一部分最優解作為子種群，新的種群期望值為：

(6)

(7)

式中：β為子種群大小；wi為正權值；xi:α為在種群的α個個體中選擇出的第i個最好個體。

(3) 更新協方差自適應矩陣。通過更新協方差自適應矩陣，引導整個種群搜索全局最優解。協方差自適應矩陣的更新公式如下:

(8)

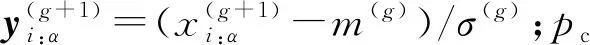
(9)

初始pc為0，pc更新過程如下：

(10)

式中：cc為進化路徑pc的學習率。

式(10)中步長σ的更新過程如下：

(11)

式中：E()為數學期望函數；I為單位矩陣；cσ為步長的學習率；dσ為步長更新的阻尼系數；pσ為步長的進化路徑，初始pσ為0，其更新過程如式(12)所示。

(12)

CMA-ES算法按上述步驟不斷循環，逐步求得最優解。

3.3 帶CMA-ES采樣器Optuna優化算法流程

Optuna具有結構簡單、優化數據方便分析等特性，但其收斂速度相對較慢，而CMA-ES算法可以通過控制步長實現快速收斂。因此，筆者將CMA-ES算法與Optuna相結合，提出帶CMA-ES 采樣器Optuna優化算法，該算法將CMA-ES采樣原理引入到Optuna中，其流程圖如圖2所示。

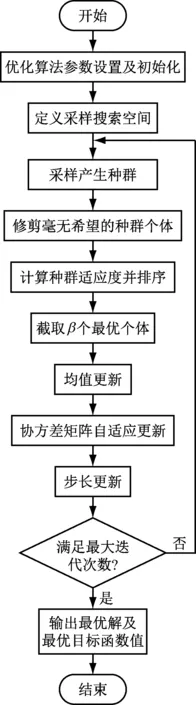
圖2 帶CMA-ES采樣器Optuna優化算法流程圖

4 仿真實驗

為驗證本文優化算法的適用性，將其與無采樣器Optuna優化的分數階PIλDμ控制、帶采樣器Optuna優化的傳統PID控制、無采樣器Optuna優化的傳統PID控制進行對比實驗，并從設定值跟蹤、抗干擾及魯棒性等方面分析SCR脫硝控制系統性能。選擇誤差絕對值積分(IAE)為目標函數，IAE的表達式如式(13)所示，首先采用臨界比例帶法整定副回路的傳統PID控制器參數，然后將控制器參數代入副回路中并將副回路等效為被控對象的一部分，最后根據上述優化算法分別獲得主回路分數階PIλDμ控制器或傳統PID控制器的參數。優化控制器參數時，Optuna迭代次數設置為100，參數類型為浮點型，獲取剪枝中位數執行的步數為50，分數階PIλDμ控制器參數的取值范圍為：KP∈[0,3.5]，KI、KD∈[0,1]，λ、μ∈[0,2]。傳統PID控制器參數的取值范圍為：KP∈[0,3.5]，KI、KD∈[0,1]。以誤差絕對值積分最小為優化目標，4種控制方案的控制器表達式如表1所示。其中G1(s)、G2(s)、G3(s)和G4(s)控制方案下的最優目標函數值分別為127.626、142.323、148.274和185.150。

誤差絕對值積分J的表達式為：

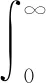
(13)

式中:t為時間。

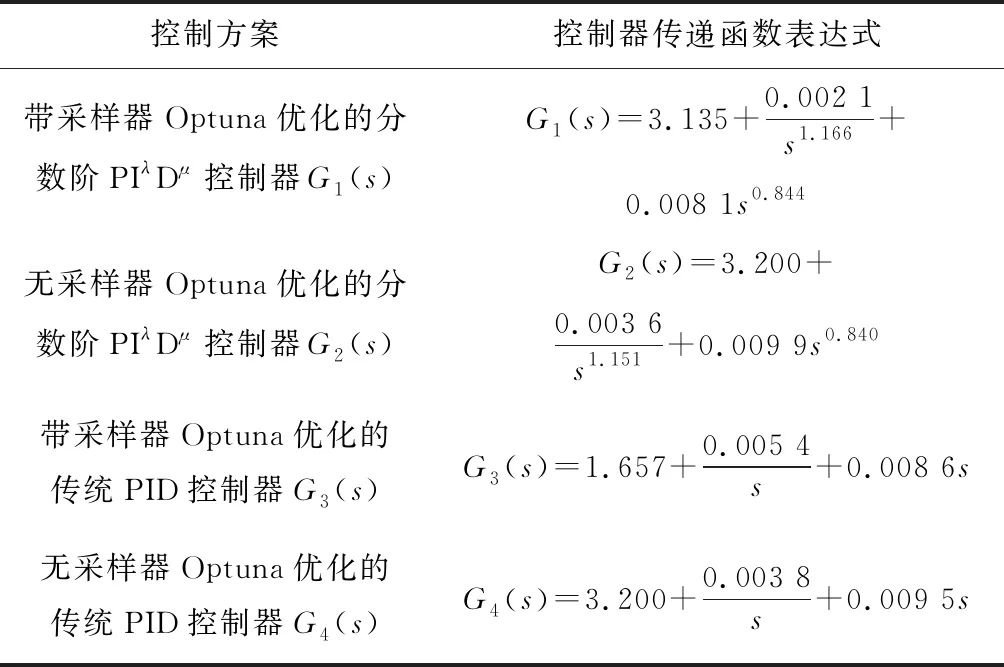
表1 4種控制方案的控制器表達式

4.1 設定值跟蹤實驗

為驗證SCR脫硝控制系統的設定值跟蹤能力，給系統加階躍設定值r=1，經過仿真后，系統在4種控制器下的單位階躍響應曲線如圖3所示，設定值誤差絕對值積分如圖4所示。

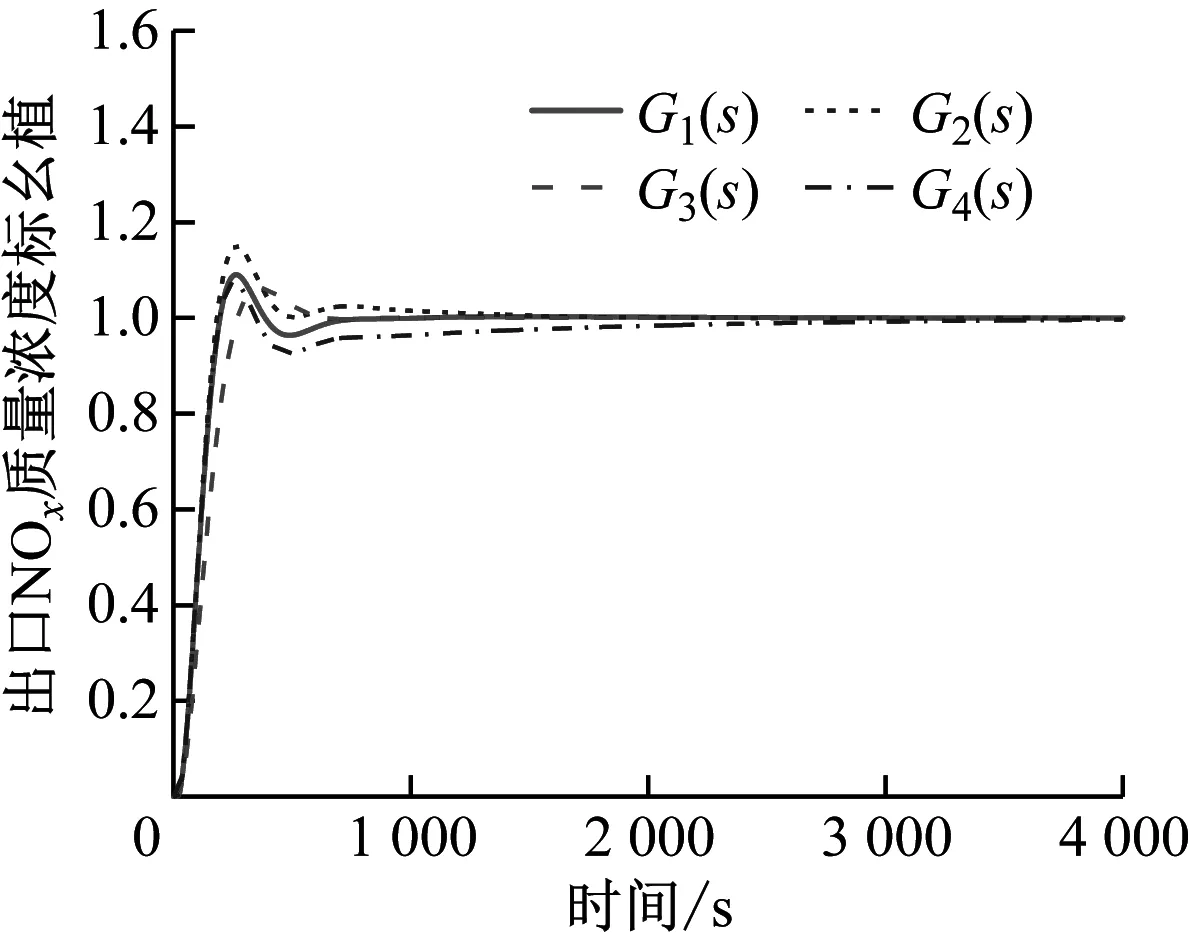
圖3 SCR脫硝系統在4種控制器下的單位階躍響應曲線

由圖3和圖4可知，4種控制方案下系統的輸出最終都能無差跟蹤設定值，與其他3種控制方案相比，G1(s)控制方案下的系統誤差絕對值積分最小，響應曲線無振蕩且能比較快速達到設定值。由此可見，帶采樣器Optuna優化的分數階PIλDμ控制系統具有較好的設定值跟蹤能力。

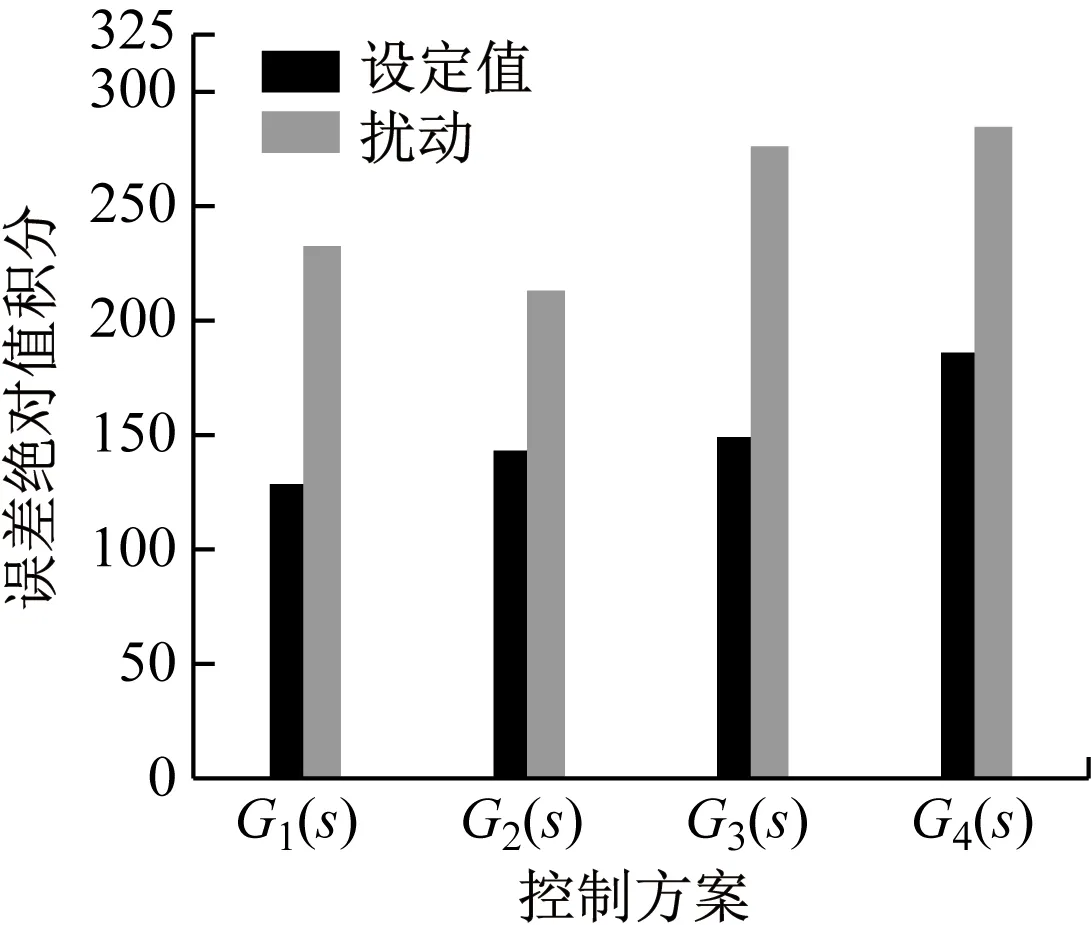
圖4 SCR脫硝系統在4種控制器下的誤差絕對值積分

4.2 抗干擾實驗

為了進一步驗證系統的抗干擾性，當t=2 000 s時，在主回路加入r=0.2的階躍擾動，系統在4種控制器下的擾動響應曲線如圖5所示。由圖4和圖5可知，SCR脫硝系統在分數階PIλDμ控制器下的誤差絕對值積分相對較小，當加入階躍擾動后，4種控制方案都具有一定的抗干擾能力，相比于其他3種控制方案，G1(s)控制方案下的系統輸出響應曲線恢復到設定值的時間較短。由此可見，該系統在分數階PIλDμ控制下的抗干擾能力更好。

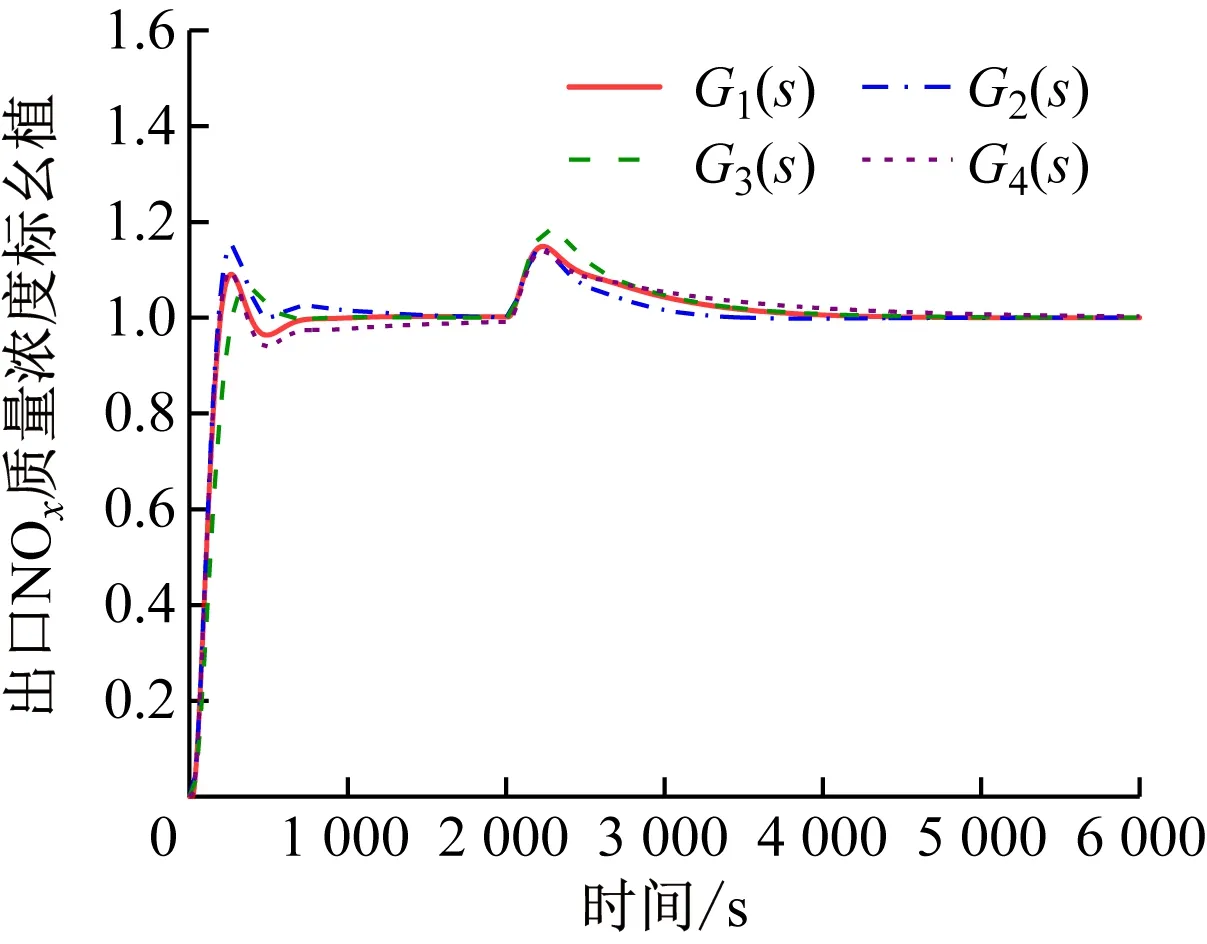
圖5 SCR脫硝系統在4種控制器下的擾動響應曲線

4.3 魯棒性實驗

在實際的工業生產中，SCR脫硝控制系統不只需要較好的設定值跟蹤和抗干擾能力，還需要較強的魯棒性。為了驗證優化算法的魯棒性，通過蒙特卡洛實驗進行檢驗[20]，并將G1(s)與G3(s)控制方案進行對比。對SCR脫硝系統主被控對象分母的二次系數發生±30%的隨機攝動，生成50個模型的被控對象簇{GM(s)}，以模擬SCR脫硝控制系統模型與實際設備之間的偏差。在單位階躍響應下G1(s)、G3(s) 2種控制方案的被控對象簇{GM(s)}輸出響應分別見圖6和圖7。

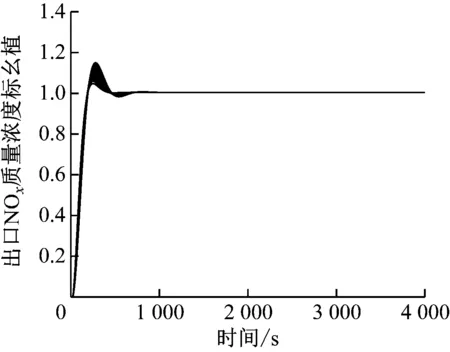
圖6 G1(s)控制方案下的蒙特卡洛實驗結果

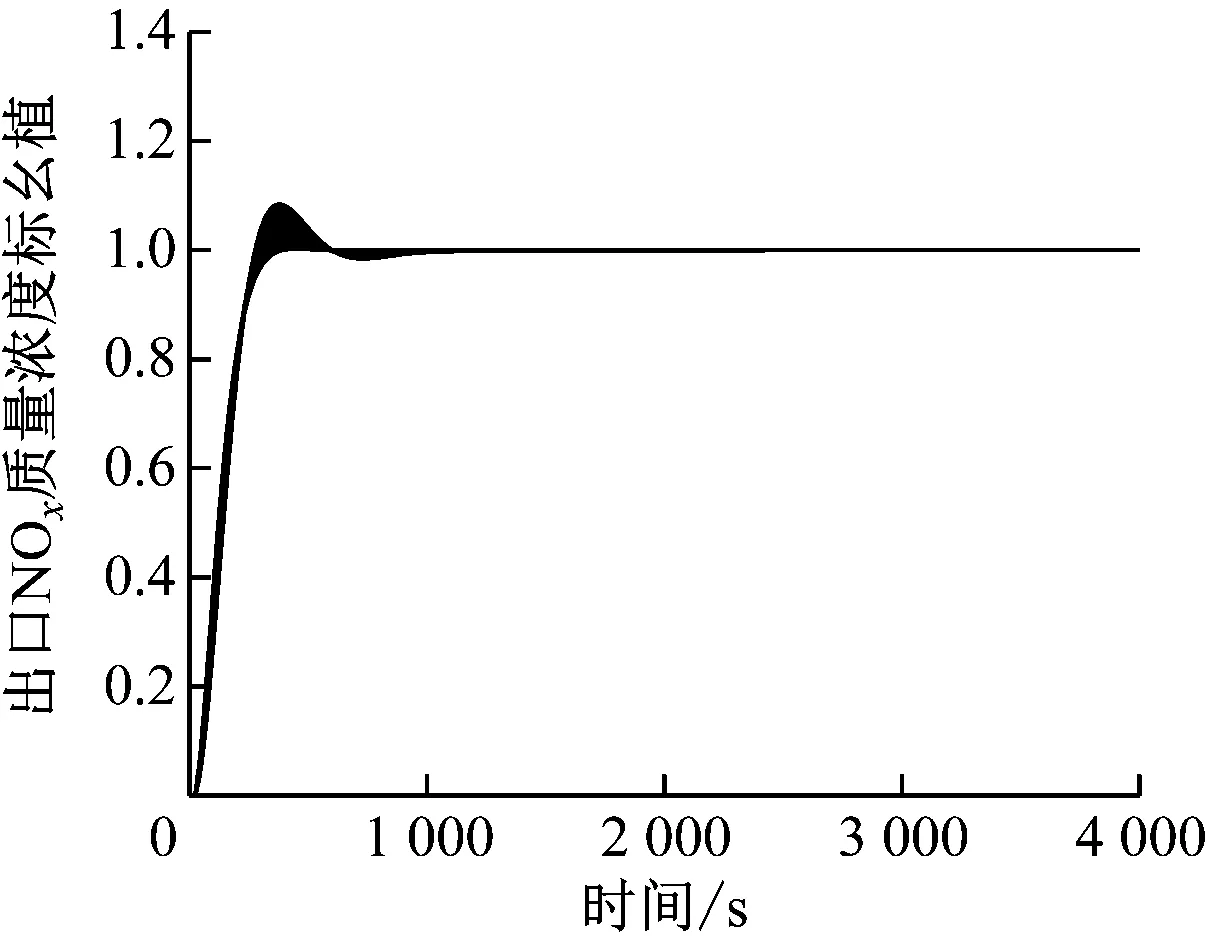
圖7 G3(s)控制方案下的蒙特卡洛實驗結果

G1(s)和G3(s) 2種控制方案下蒙特卡洛實驗性能指標分布如圖8所示，2種控制方案下設定值階躍的系統性能參數如表2所示。從圖3～圖8和表2可得：所提出的G1(s)控制方案的調節時間遠小于傳統PID控制，且其超調量也相對較大，但超調量的標準差相對較小，表明G1(s)控制方案的魯棒性較強。當主回路被控對象分母的二次系數發生±30%的隨機攝動時，G3(s)控制方案下的點集相對分散，分布在2個區域，而G1(s)控制方案下的點集相對集中，且G1(s)控制方案的調節時間和超調量的標準差都比G3(s)控制方案小。因此，帶采樣器Optuna優化的分數階PIλDμ控制具有較強的魯棒性。

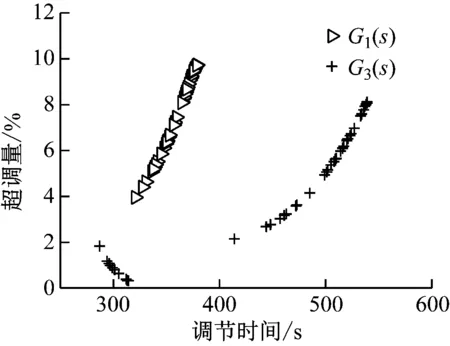
圖8 2種控制方案下設定值階躍的蒙特卡洛實驗性能指標分布

表2 2種控制方案下設定值階躍的系統性能和魯棒性指標統計表

綜合SCR脫硝系統在設定值跟蹤、抗干擾和魯棒性3個方面的分析驗證，SCR脫硝系統采用帶采樣器Optuna優化的分數階PIλDμ控制具有更好的控制效果。相對于傳統PID控制，分數階PIλDμ控制器以其較好的設定值跟蹤能力，實現了SCR脫硝系統噴氨量的精確控制，延長了設備的使用壽命。所提出的SCR脫硝控制方案因其強抗干擾和強魯棒性，有效地降低了未知不確定性因素對系統造成的影響。

5 結 論

針對SCR脫硝系統存在的強擾動和不確定的特性，提出了帶CMA-ES采樣器Optuna優化的分數階PIλDμ控制方案。利用仿真實驗驗證了分數階PIλDμ控制器的控制效果，并與帶采樣器Optuna優化的傳統PID控制、無采樣器Optuna優化的分數階PIλDμ控制及傳統PID控制方案進行對比。結果表明，帶CMA-ES采樣器Optuna優化分數階PIλDμ控制方案在火電廠SCR脫硝控制系統中具有良好的設定值跟蹤能力、抗干擾能力及魯棒性，本方案更適合應用于SCR脫硝控制系統。