基于改進自適應多元變分模態分解的軸承故障診斷方法研究

時培明， 張慧超， 韓東穎

(1.燕山大學 電氣工程學院，河北秦皇島 066004；2.燕山大學 車輛與能源學院，河北秦皇島 066004)

旋轉軸承是機械設備中非常重要的一部分，由于惡劣的工作環境，其出現故障的概率較其他部件更高[1]。因此，對滾動軸承進行狀態檢測和早期故障診斷尤為重要。

變分模態分解(VMD)在實際工程中的應用得到了廣泛關注。Dragomiretskiy等[2]首次提出VMD，從根本上解決了經驗模態分解(EMD)缺乏扎實數學依據的問題，且該算法不會出現端點效應和模態混疊現象。Zhang等[3]將VMD與集成深度置信網絡相結合，對風電機組軸承故障頻率進行了特征提取、分類和診斷。Wang等[4]提出了一種VMD參數優化方法，并應用到齒輪箱的故障診斷上。李帥永等[5]將VMD與互譜分析相結合，并應用在供水管道泄漏定位方面。Li等[6]提出了一種將VMD與卷積盲源分離相結合的多維變分分解(MDVD)方法，并將其應用在風電機組的維護上。Rehman等[7]提出了一種多元變分模態分解(MVMD)算法，并證明了該方法在信號處理方面有很大的優勢。Rehman等[8]提出一種多通道信號同時自適應處理的多元經驗模態分解(MEMD)算法,Rilling等[9]提出二元經驗模態分解(BEMD)算法,Rehman等[10]提出三元經驗模態分解(TEMD)算法，以上算法均繼承了EMD原有的特點，Lü等[11-12]在此基礎上進行了優化，對端點效應和模態混疊現象進行了一定程度的改進，但還不能從根本上解決問題。

筆者提出一種自適應多元變分模態分解(AMVMD)方法，將MVMD與灰狼算法(GWO)[13]相結合，以最小平均包絡熵(MAEE)為適應度函數，對分解參數進行尋優處理，選取分解模態的最優分量進行信號重構，并將其與Teager能量算子(TEO)相結合，實現對特征頻率的增強和識別，通過仿真信號和實際數據驗證該方法的可行性和優越性。

1 AMVMD

AMVMD通過交替方向乘子法來實現模態的最小化，保證多維信號之間相同中心頻率的帶寬之和最小，相應的約束表達式為：

(1)

式中：t為時間；xc(t)為通道c的原始信號；C為通道個數；k為信號分解的本征模態數；uk,c為通道c的第k模態分量；wk為第k模態的中心頻率。

在式(1)中引入拉格朗日乘法算子，將約束問題轉變為非約束問題，相應的增廣拉格朗日表達式如下：

L({uk,c},{wk},λc)=

(2)

式中：α為懲罰因子；λc為拉格朗日乘法算子；L()為增廣拉格朗日函數;u+,k,c為復合信號。

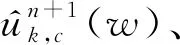
(3)

(4)

(5)

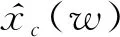
MVMD分解結果主要與本征模態數k和懲罰因子α有關，AMVMD的意義在于消除人為經驗參數設置對分解結果的影響，使算法可以根據信號本身特點自適應尋求最優參數，并按照最優參數進行模態分解，從而達到最好的效果。GWO相比于其他優化算法具有優化效率高、時間短、收斂速度快等優勢[11]，因此將其用于MVMD的參數尋優。

GWO的啟發來源于狼群狩獵行為，按照適應度函數從大到小排列，將狼群分為4個等級，即al、bl、cl和dl，目標函數的最優解依次由al、bl和cl來決定，dl來執行，通過不斷迭代更新，最終實現狩獵，找到最優解。GWO的位置更新公式為：

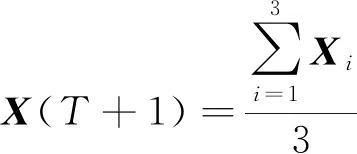
(6)

X1=Xal-A1·Dal

X2=Xbl-A2·Dbl

X3=Xcl-A3·Dcl

Dal=|C1·Xal-X|

Dbl=|C2·Xbl-X|

Dcl=|C3·Xcl-X|

式中：C1、A1均為當前狼群al的協同系數向量;C2、A2均為當前狼群bl的協同系數向量;C3、A3均為當前狼群cl的協同系數向量；X為當前迭代次數中的最優解；Xal、Xbl和Xcl分別為狼群al、bl、cl的當前位置向量；T為迭代次數。

采用MAEE作為適應度函數，對MVMD算法的參數進行尋優。

(7)

(8)

(9)

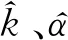
AMVMD的細節過程見圖1。其中，Tmax為最大迭代次數。

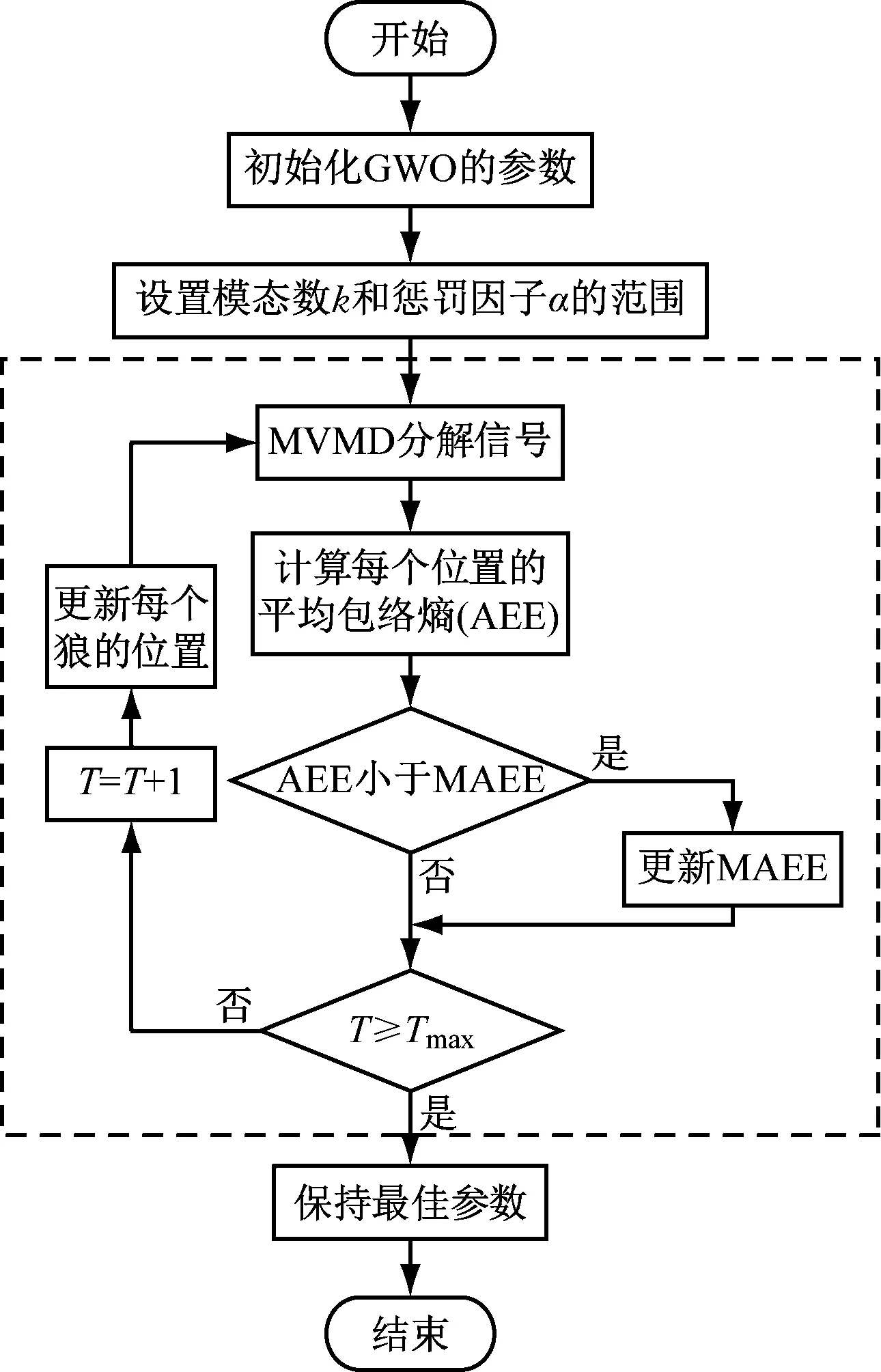
圖1 AMVMD流程圖

2 AMVMD與TEO相結合的特征識別

TEO是一種捕捉信號瞬時變化的非線性差分算子[12]。對于信號x(n)，TEO為：

ψc(x(n))=x2(n)-x(n-1)x(n+1)

(10)

式中:ψc為能量算子。

與傳統的能量定義相比，TEO的結果同時考慮了信號的瞬時幅度和瞬時頻率。由于滾動軸承瞬態沖擊的振動頻率較高，TEO能有效地提高瞬態沖擊成分。

引入2個指標作為信號重構的判斷依據，分別是樣本熵和相關系數。樣本熵越大，表示時間序列越復雜。對于由N個數據組成的時間序列{x(n)}，樣本熵的計算步驟如下：

(1) 按序號組成維數為m的向量序列{Xm(i)}，其中Xm(i)=(x(i),x(i+1),…,x(i+m-1))，1≤i≤N-m+1。

(2) 定義向量Xm(i)與Xm(j)之間的距離d為兩者對應元素中最大差值的絕對值。

(3) 對于給定的Xm(i)，統計d不大于相似容限r的j的數目Ai,1≤j≤N-m,j≠i。

(11)

式中:Am(r)為2個序列在相似容限r下匹配m個點的概率。

(4) 將維數增加到m+1，計算Xm+1(i)與Xm+1(j)之間距離不大于r的個數，記為Bi。

(12)

式中:Bm(r)為2個序列匹配m+1個點的概率。

當N為無限值時,將樣本熵SampEn(m,r)定義為：

(13)

當N為有限值時，樣本熵可以用下式估計：

(14)

取各個模態分量與原始信號的相關系數cr來評估其相關程度，具體公式如下：

(15)

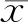
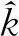
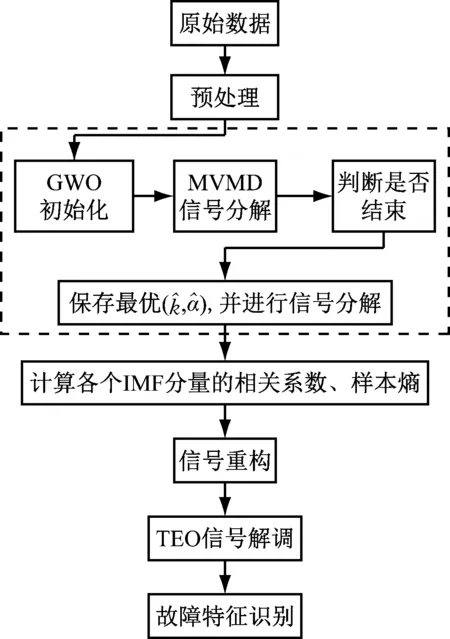
圖2 AMVMD-TEO框架結構圖

3 實驗分析

3.1 仿真信號分析

采用仿真信號對AMVMD算法進行實驗驗證，仿真信號x(t)、y(t)分別為通道1和通道2的輸入信號，信號采樣點為3 000，采樣頻率為6 kHz，其仿真信號時域圖見圖3。其中，A為振動信號加速度幅值。

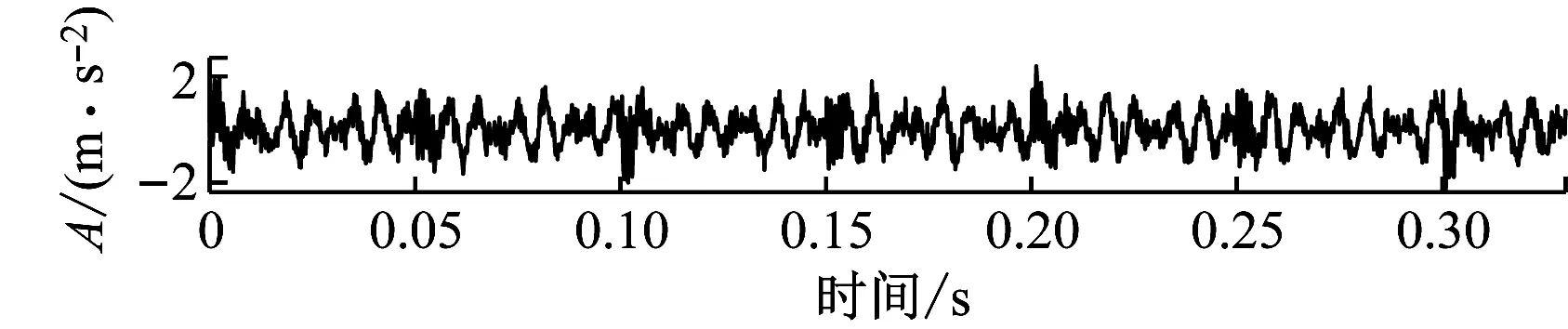
(a) 通道1

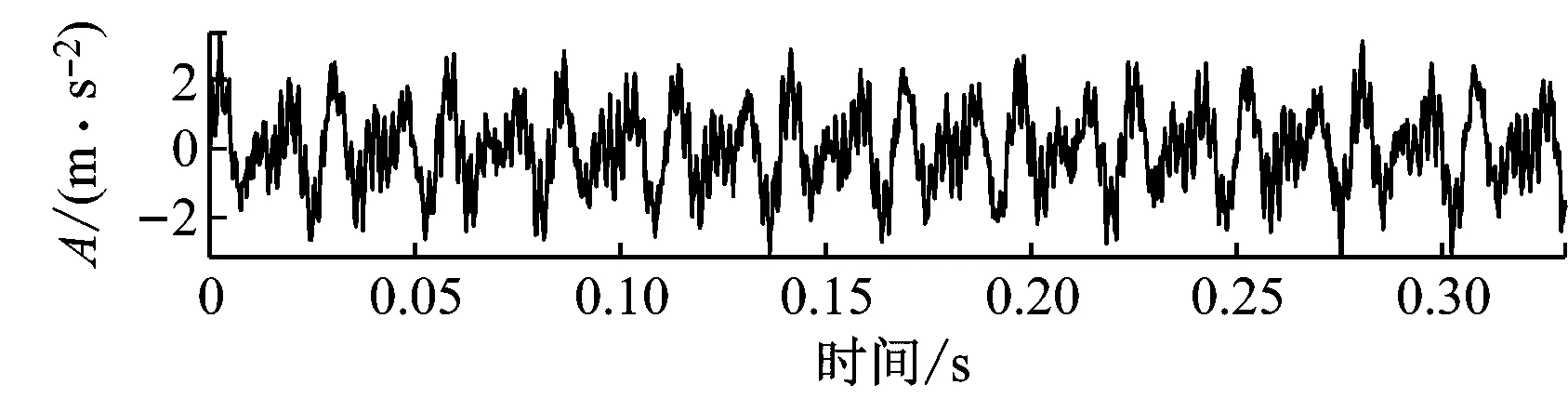
(b) 通道2

分別采用AMVMD算法和MEMD算法對仿真信號進行分解。

x(t)=0.85cos(2π×72t)+cos(2π×25t)×

sin(2π×150t)+1.25exp(-200t)sin(2π×

1 000t)+nnoise(t)

(16)

y(t)=cos(2π×25t)sin(2π×500t)+sin(2π×

72t)+sin(2π×108t)+nnoise(t)

(17)

式中：nnoise(t)為在原始信號的基礎上添加10 dB的高斯白噪聲信號。

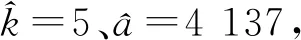
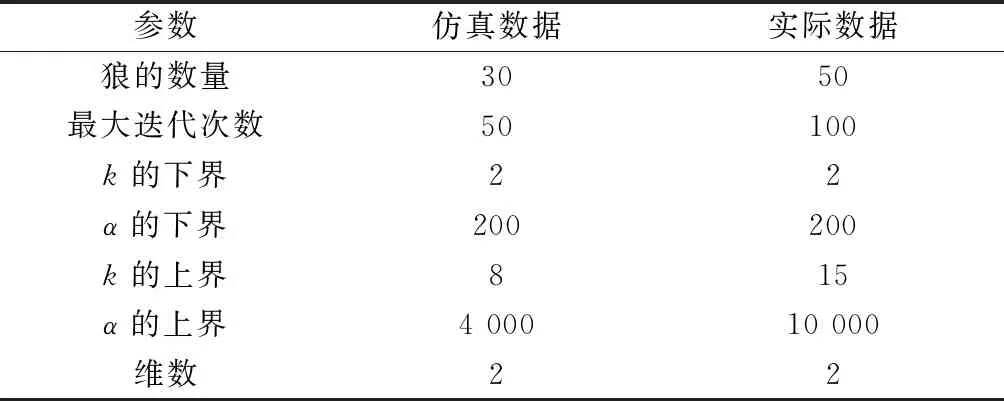
表1 GWO參數設置

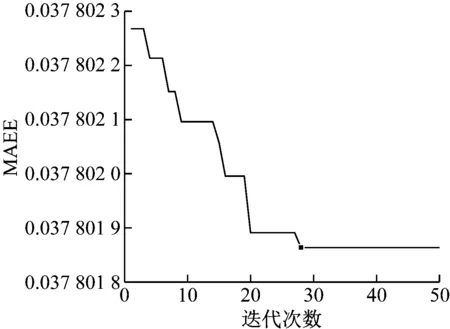
圖4 仿真信號收斂過程

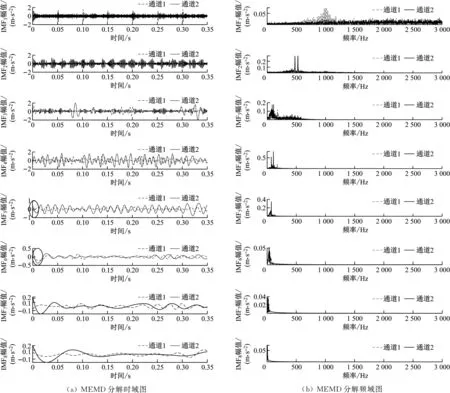
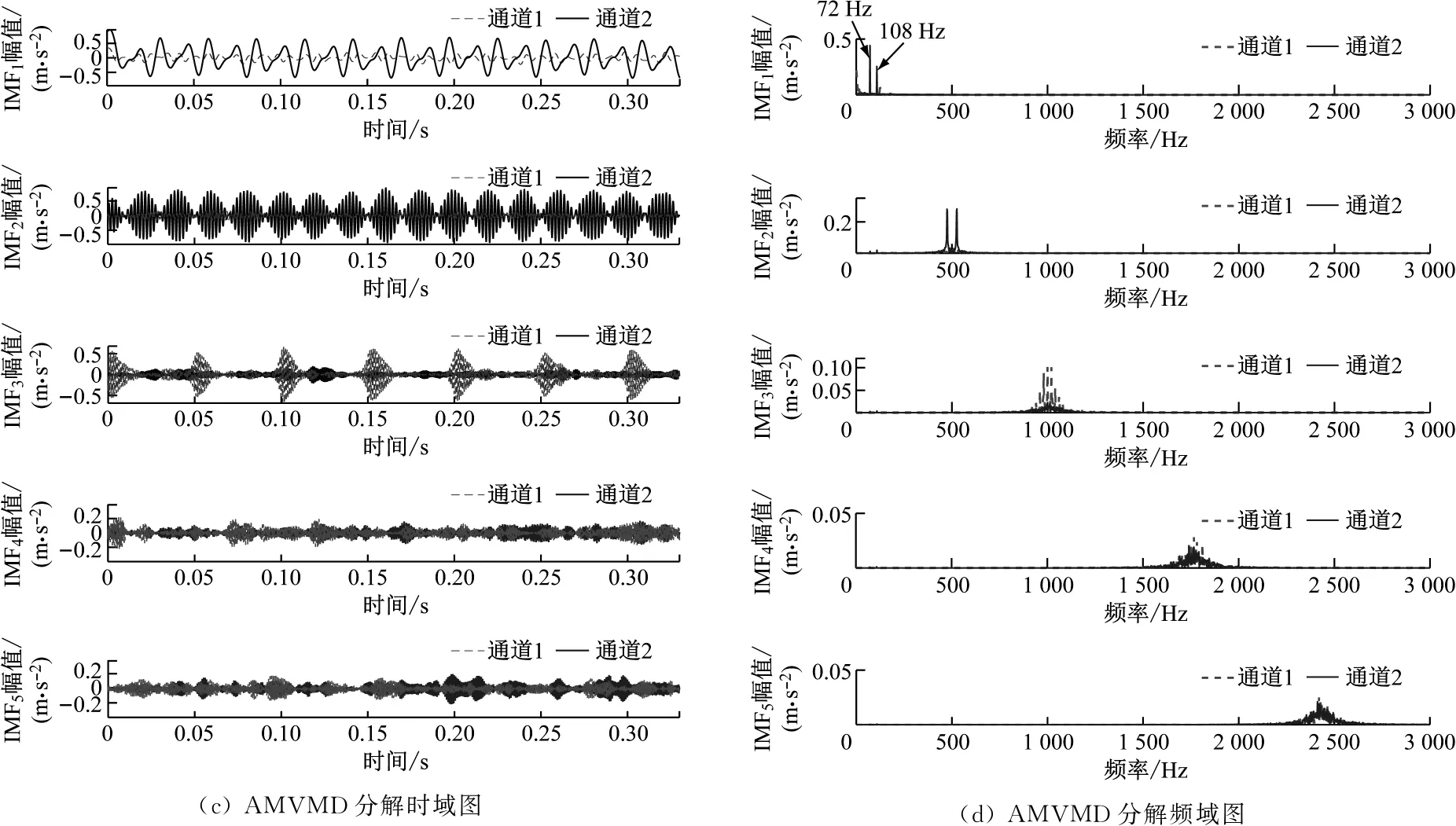
圖5 仿真信號分解結果對比

3.2 實際數據分析

為了更好地說明所提出方法的有效性，采用實際軸承故障實際數據[14]進行驗證。實驗中軸承型號為ZA-2115，軸承節徑為71.501 mm，滾子數為16，接觸角為15.17°，滾珠直徑為8.407 mm，計算可得軸承的外圈故障頻率為236.4 Hz，內圈故障頻率為297 Hz，滾動體故障頻率為140 Hz，實驗平臺模型和工況圖見圖6。 2個高靈敏度石英ICP加速度計安裝在軸承座上，其采樣頻率為20 kHz，測試過程中的轉速為2 000 r/min，在軸承上施加6 000 N的徑向載荷。Qiu等[14]評估軸承的性能退化時發現，軸承約在5 300 min時開始體現性能退化，這意味著早期故障信號出現在5 300 min之前。因此，分別選取外圈、內圈和滾動體故障時刻的實際數據進行實驗驗證。

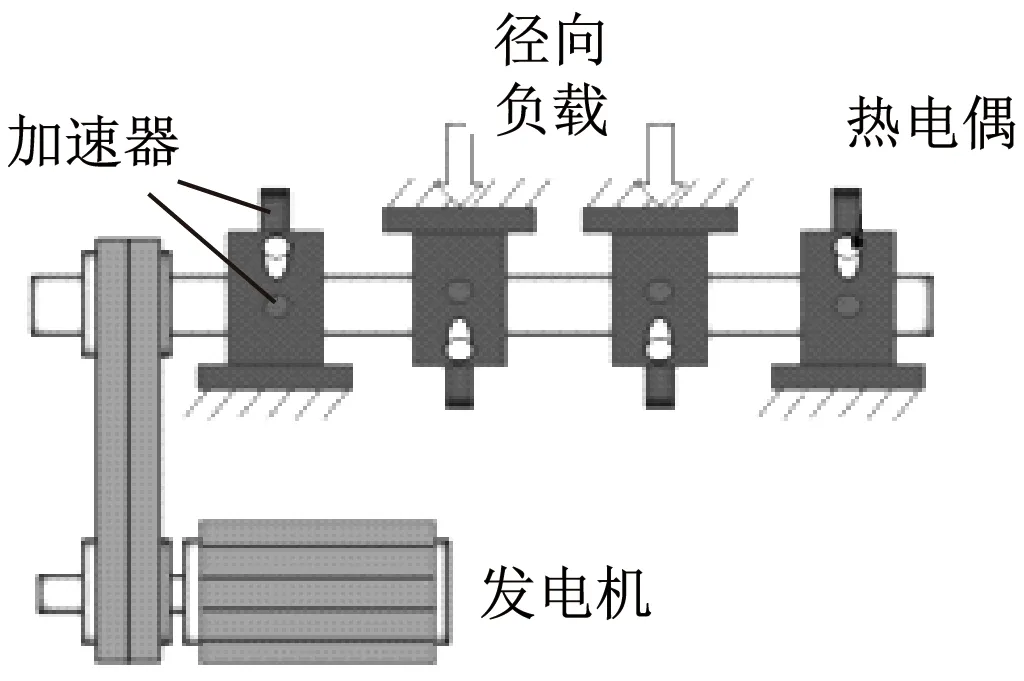
(a) 測試平臺模型

(b) 實際數據采集

圖7為原始數據的時頻圖。內圈信號時域圖中沒有觀察到明顯的周期信號，結合頻域圖可以看出，樣本信號中有許多噪聲干擾；同樣地，滾動體信號較內圈信號更加雜亂無章，噪聲干擾強度更大；外圈信號中噪聲幅值較小，但在頻域圖中也沒有出現明顯的特征信號。因此，將這3種信號分別采用AMVMD和MEMD算法進行模態分解，來驗證AM-VMD算法的特征提取能力。

AMVMD和MEMD算法的信號分解結果見圖9。采用AMVMD算法分解的有效信號主要集中在IMF4和IMF5中，周期性信號集中在前3個模態分量中。采用MEMD算法分解的模態分量數有11個，由于空間有限，選取前8個模態分量進行可視化，見圖9(c)和圖9(d)。由圖9可知，有效模態分量主要集中在后6個模態分量中，結合其頻譜圖可以看出，IMF1～IMF5的頻帶寬度很大，且時域圖中對應的模態信號雜亂無章，無周期性規律，這為有效信號的特征提取帶來了很大的挑戰。

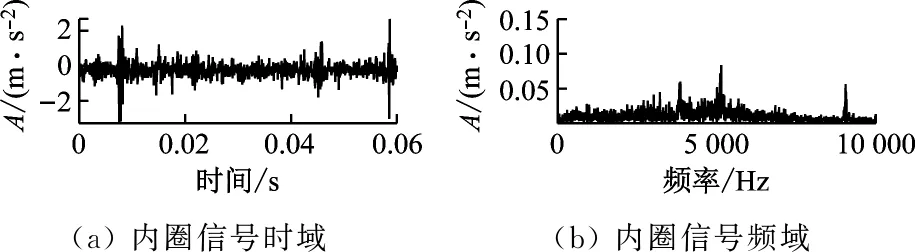
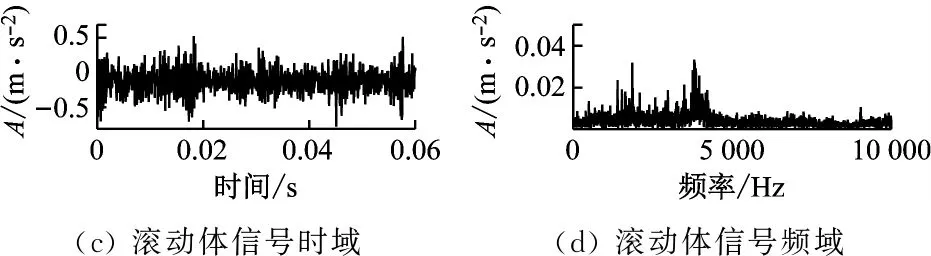
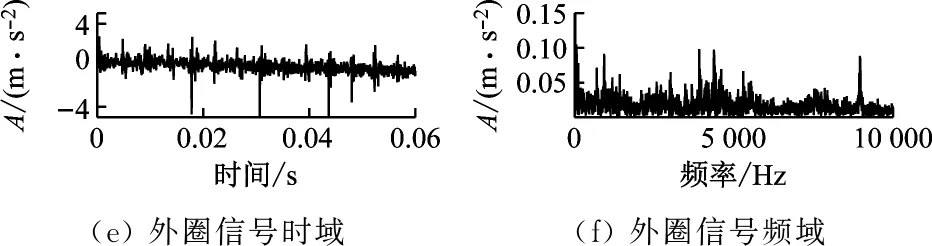
圖7 原始數據時頻圖

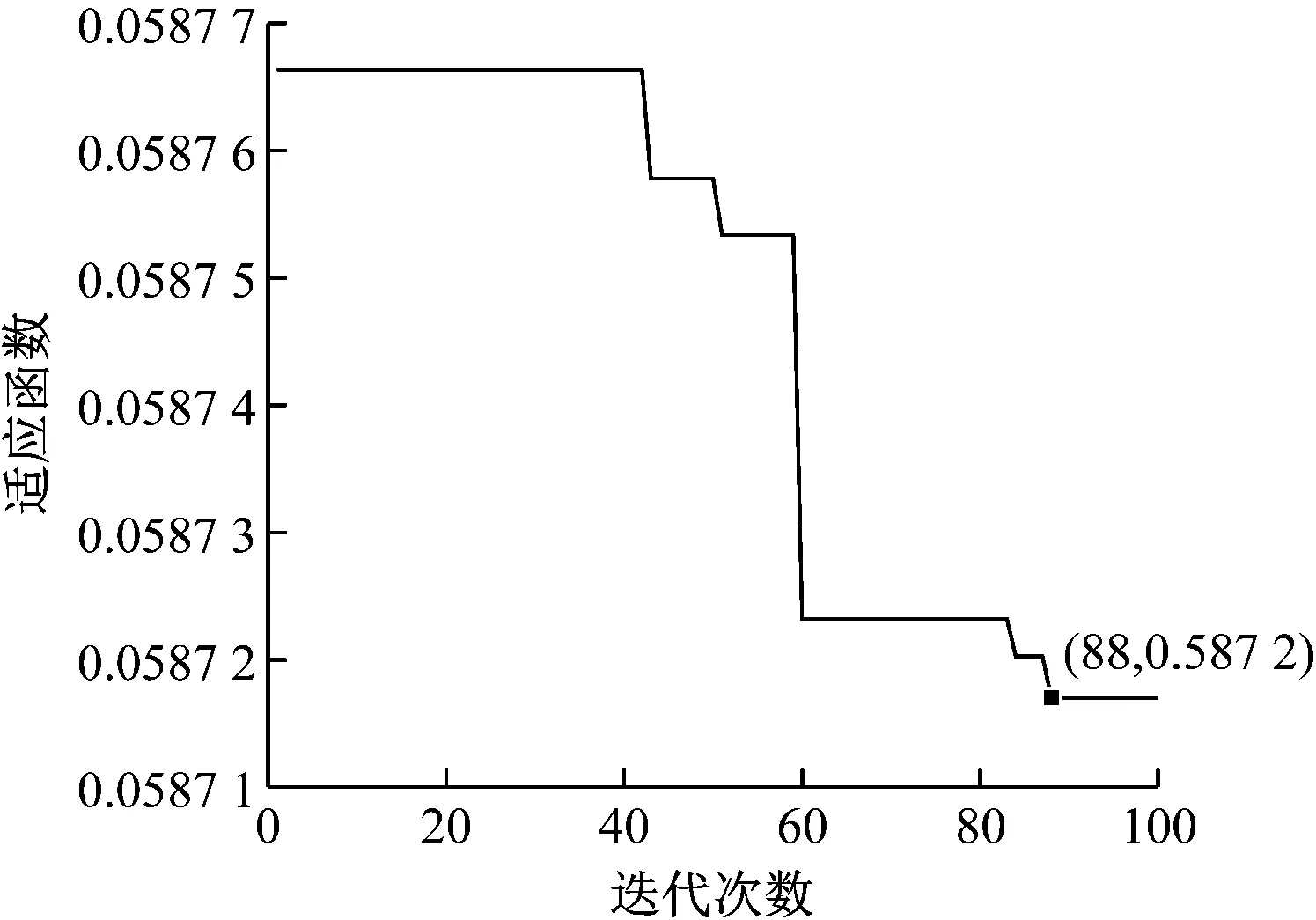
圖8 優化算法收斂過程

采用AMVMD和MEMD算法得到模態分量的樣本熵和相關系數,結果見表2。由于篇幅有限，選取每種類型最佳的3個模態分量。按照樣本熵與相關系數平權的情況綜合考慮，選取最優的2個模態分量進行信號重構，由TEO解調來增強周期性沖擊分量，最終識別故障特征頻率。

對采用AMVMD和MEMD算法分解后的各模態分量進行互相關系數分析。由于MEMD算法分解的IMF11為殘余信號，IMF9和IMF10與原始信號的相關性較小，因此選取IMF1～IMF8的模態分量進行擬正交分析，結果見圖10。

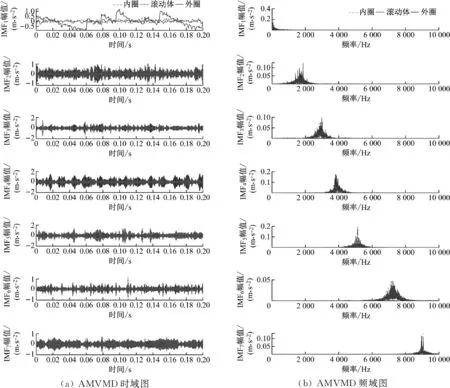
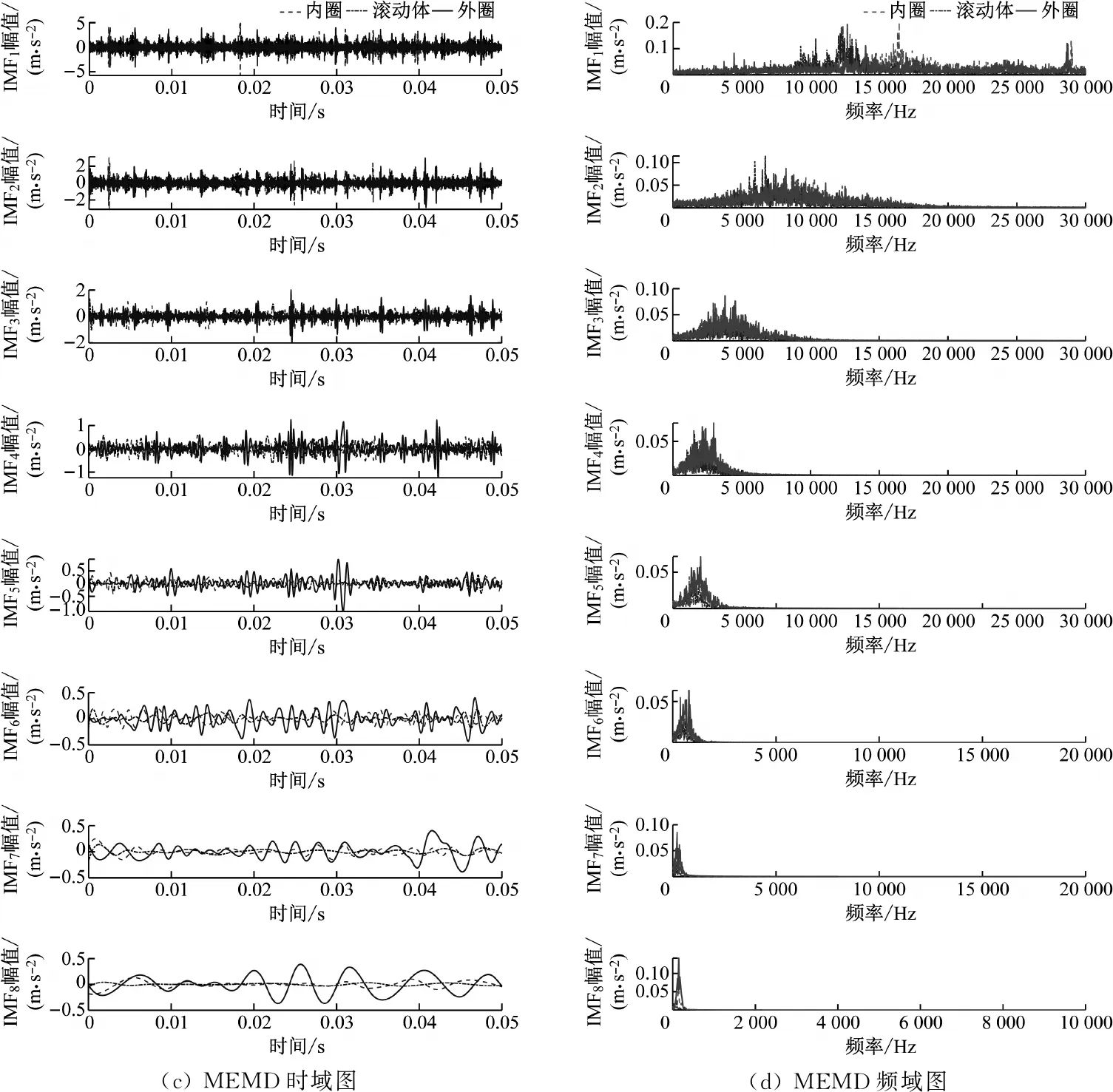
圖9 采用AMVMD和MEMD算法得到的分解結果時頻圖

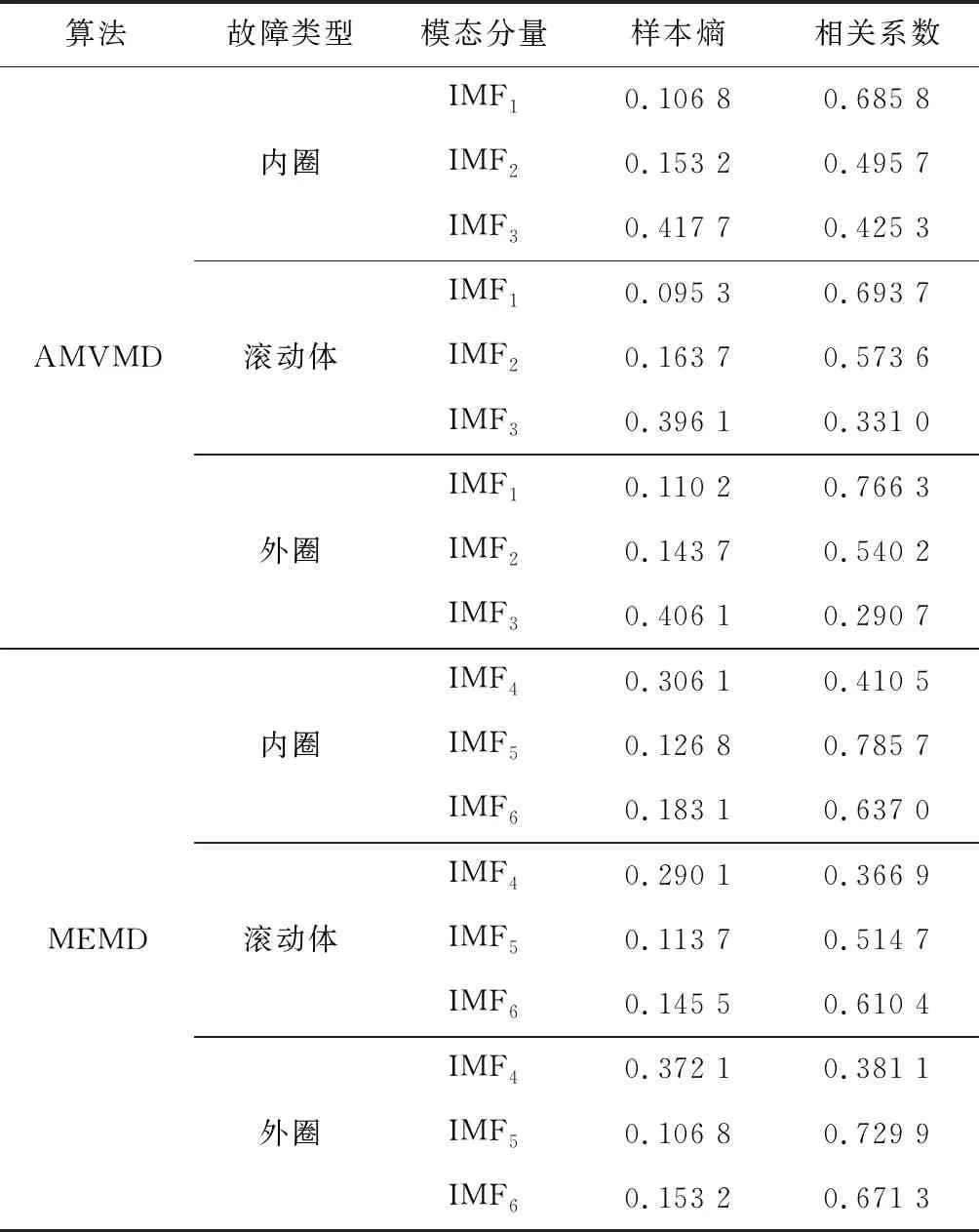
表2 模態分量的樣本熵和相關系數

(18)

式中：ρij為同源信號IMFi與IMFj的互相關系數；IIMFi為同源信號的第i個模態分量；IIMFj為同源信號的第j個模態分量；σi為IMFi信號的標準差；σj為IMFj信號的標準差。

如果互相關系數為0，則說明模態分量間是準正交的；如果互相關系數接近1，表明模態分量間相關性非常強。從圖10可以看出，采用AMVMD算法時，擬正交矩陣呈對角結構，表明AMVMD算法分解的各模態分量間有很強的準正交性；對于MEMD算法分解信號的各模態分量互相關系數矩陣，相鄰模態分量間有一些“泄漏”，與上文分析結果一致，在IMF3與IMF4以及IMF5與IMF6之間均存在不同程度的混疊，方形矩陣的對角性質也可以說明MEMD分解的模態分量之間存在混疊現象。

圖11為采用AMVMD和MEMD信號重構后的包絡結果。在MEMD的包絡結果中，噪聲干擾較小，但內圈故障、滾動體故障和外圈故障3種故障信號重疊在一起，無法進行相應的特征識別。采用AMVMD的包絡結果中噪聲能量較大，但3種故障信號的特征幅值也很突出，大大降低了特征提取的難度。

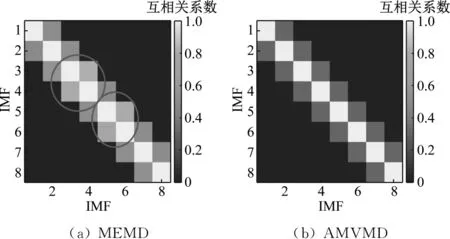
圖10 各模態分量的擬正交對比圖

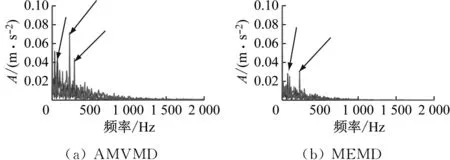
圖11 信號重構的包絡圖

為更好地對以上結果進行量化比較，引入幅值、信噪比和譜功率放大系數3個指標來判斷所提方法在故障信號處理方面的優劣，結果見圖12。從圖12可以看出，與MEMD和MVMD算法相比，AMVMD算法無論在故障信號的幅值、信噪比還是譜功率放大系數方面均有很大程度的提升，能夠更好地識別故障頻率。因此，所提的AMVMD算法在故障特征提取方面更具有優越性。

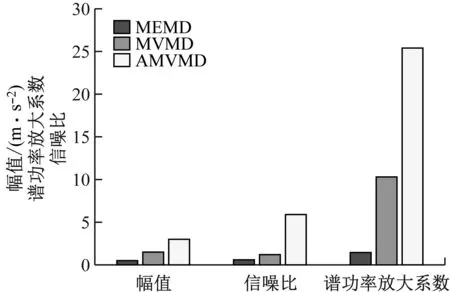
圖12 3個指標的對比

4 結 論

與MEMD分解效果相比，利用所提的AMVMD算法對復雜的軸承故障信號進行分解可以有效克服模態混疊和端點效應，將分解后的模態分量以樣本熵和相關系數為指標進行信號重構，與TEO相結合，以增強微弱的瞬時沖擊成分并識別故障特征頻率。實驗證明，本文所提方法無論在軸承故障信號的幅值、信噪比，還是在譜功率放大系數方面均有很大的改進和提升，不僅可以有效地對軸承故障信號進行特征提取，也為下一步的故障識別提供了新的途徑。