基于BSO-BPNN模型的電能計量裝置異常診斷方法研究

朱少斌，許素安，馬宗彪，王 晶

(中國計量大學，浙江 杭州 310018)

0 引 言

隨著國網公司在電力物聯網建設工作中的部署，當前供電企業的用電信息采集系統已存儲了大量能用于計量裝置異常診斷的信息[1-2]。為了提高計量裝置的診斷效率，同時降低運維人員工作量，研究如何根據存儲的信息進行裝置的異常狀態在線診斷具有重要意義。

目前針對電能計量裝置建立的診斷模型大多是一種綜合評價模型，如妙紅英等[3]建立四種健康狀態模型，根據隨機森林算法對計量裝置進行狀態評估，判定計量裝置的運行狀態。盧健豪等[4]利用層次分析法和1-9標度法構建電能計量裝置評價體系，得到計量裝置的運行狀態模糊評價結論。這些綜合評價方法得到的結論只能對電能計量裝置運行狀態進行大致判定，適用范圍較窄，實際應用性不強。對于可能造成用電客戶經濟安全損失的電能計量裝置電流電壓異常等重要異常狀態無法進行準確判定，電網運維人員也無法根據這種模糊的結論得到具體的電能計量裝置異常狀態，不能及時對電能計量裝置的異常進行處理。所以文章建立一種能夠方便準確診斷電能計量裝置實際異常狀態的模型具有特別重要的意義。

近年來，BP神經網絡（BPNN）模型成功應用于故障診斷領域，但仍存在許多不足，故障診斷性能不佳。粒子群算法（PSO）作為一種新型群體智能優化算法，常用來優化BP神經網絡模型的診斷性能，比如李達等[5]根據PSO-BP算法實現了高壓輸電線路的異常故障分類，減少尋找故障點所需要的時間；李升健等[6]利用CPSO-BP算法對配電網進行故障選線，使選線結果的精度得到了提高。PSO算法雖然具有結構簡單，調參較少等優點，但其粒子更新規則容易導致算法陷入局部最優，出現早熟等問題。為了提升PSO的優化性能，文章在原PSO算法的粒子更新規則中加入了天牛須搜索算法（BAS）的個體速度、位置更新規則，以此增強算法的收斂速度和個體搜索能力。文章結合PSO和BAS的優勢建立天牛群優化BP神經網絡的診斷模型（BSOBPNN），使用BSO-BPNN診斷模型對電能計量裝置實際發生的異常進行診斷。

1 電能計量裝置異常診斷模型

在電力系統中，電能計量裝置是不可或缺的重要組成部分之一，其大多數異常都可根據用電信息采集系統采集到的巡檢數據進行判斷。巡檢數據作為反映客戶電能計量裝置運行狀態的瞬時值，若采集到的兩次巡檢數據一樣，則可用巡檢數據來反映計量裝置的運行狀態，通過分析裝置的異常狀態可知，巡檢數據中三相三線電能計量裝置的三相電壓數據、三相電流數據和電壓比值、電流比值等10個參數（分別用x1～x10表示）為主要特征參數。

電能計量裝置結構復雜，故障類型多樣，根據巡檢數據可將計量裝置分為9種異常，以這9種異常（分別為F1～F9），加上正常狀況（用F10表示），作為待診斷的10種狀態類型，以這10種狀態類型為分類標準，驗證該模型的可行性和有效性。電能計量裝置異常與特征參數的表現存在交叉和重疊，通過BSO-BPNN模型可實現裝置異常的準確識別。電能計量裝置異常診斷模型中特征參數x1～x10為網絡輸入，網絡輸出為待診斷狀態類型F1～F10（見圖1）。

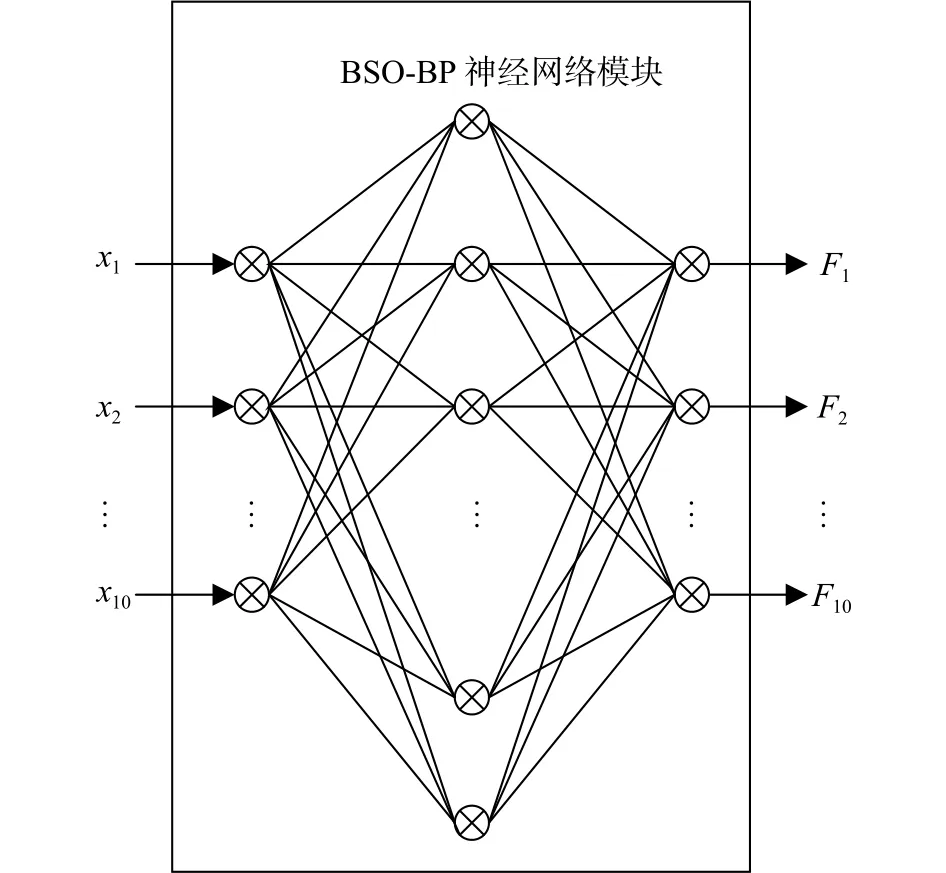
圖1 電能計量裝置異常診斷模型圖

2 算法原理概述

2.1 BP神經網絡

BP神經網絡[7]的特征是輸入正向傳播，誤差反向傳播，其網絡可在多次訓練學習中不斷改變自身的結構參數，以使輸出誤差滿足要求。設BP神經網絡的輸入為X=[x1, ···,xi, ···,xn]T，F=[F1,···,Fk, ···,Fq]T為網絡輸出，n，m，q分別為 BP 神經網絡模型中輸入層、隱含層、輸出層的神經元個數；vij為輸入層到隱含層的權值；b1為隱含層的閾值；wij為隱含層到輸出層的權值；b2為輸出層的閾值；h(x)為隱含層節點所采用的傳遞函數；f(x)為輸出層節點所采用的傳遞函數。則BP神經網絡的輸入、輸出關系可表示為：

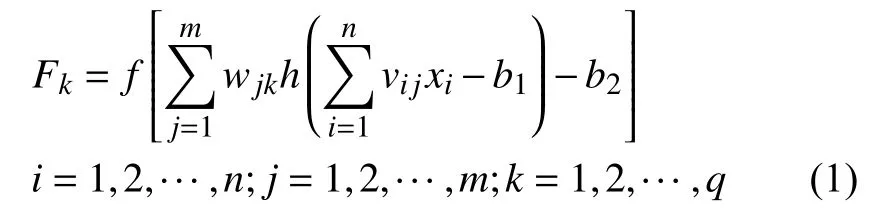
網絡輸出總誤差函數為：

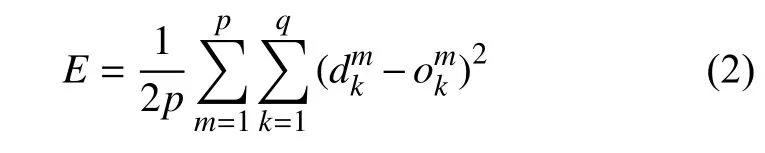
式中：p——所含樣本總數；

d——期望輸出值。

2.2 粒子群優化算法

Eberhart和Kennedy在1995年提出了粒子群算法[8-9]。PSO算法是由鳥群覓食行為啟發而來，并對覓食行為進行建模而得到的優化算法，主要用于解決最優化問題。在PSO的尋優過程中，將問題所有解的空間看作鳥群尋找食物的空間，并用無體積和質量的粒子來表示每一只鳥。每只鳥經過的位置都作為問題存在的可能性解，當鳥類中的個體尋覓到食物時，即優化問題找到了最優解。假設一個N維的搜索空間，以Vi=[vi,1,vi,2, ···,vi,N]表示第i個粒子的速度，以Xi=[xi,1,xi,2, ···,xi,N]表示第i個粒子的位置。在每一次的迭代中，根據各個體的目標函數值，判斷t時刻各個體所經過的個體最優位置pbest，以及整個群體所找到的最優位置gbest。PSO算法中的每個粒子都根據pbest和gbest來更新各自的速度和位置，如下式所示：

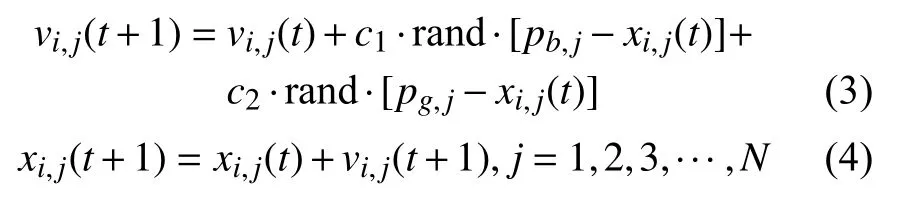
式中：t——當前更新次數；

c1、c2——更新的學習因子；

rand——0～1之間的隨機數。

2.3 天牛須搜索算法

Jiang和Li等在2017年提出了天牛須搜索算法[10-11]。BAS算法的思想源于對天牛覓食行為的研究，當天牛開始覓食時，它并不清楚食物所在的具體位置，而是利用它聞到的食物氣味來尋找食物。把食物氣味看做一個函數，天牛根據自身左右兩觸角聞到的氣味強弱值，朝氣味強的一邊移動，通過不斷朝更強的方向移動，進而找到整個空間中氣味值最強的點。算法具體步驟如下：

1) 對BAS中的天牛隨機搜索向量進行歸一化處理：

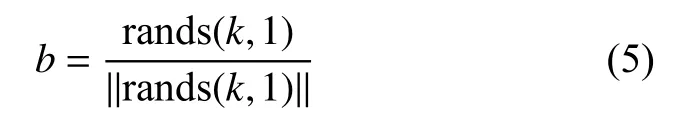
式中：b——天牛須隨機方向向量；

rand( )——隨機函數；

k——空間維度。

2) 創建天牛左右須空間坐標：

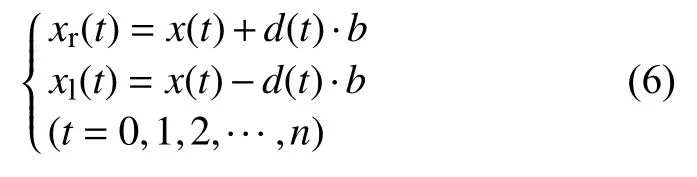
式中：xr(t)、xl(t)——天牛右觸和左觸第t次更新時的空間坐標；

x(t)——個體第t次更新時的空間坐標；

d(t)——第t次更新時兩觸之間的距離。

3) 根據目標函數f(x)判斷兩須之間氣味的強度大小，創建天牛須位置移動模型：

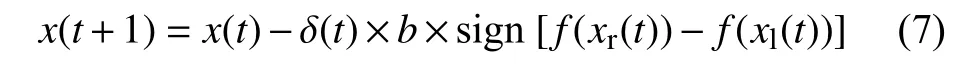
式中：x(t+1)——第t+1次更新時天牛的空間坐標；

δ(t)——第t次更新時的步長因子；

sign(x)——符號函數；

f(xr(t))、f(xl(t))——天牛左、右兩觸的目標函數值。

3 基于BSO-BPNN模型的電能計量裝置異常診斷

3.1 天牛群算法

BAS算法注重個體，忽略了群體之間的連接，PSO算法則側重整個群體對于個體的影響，不考慮搜索過程中個體自身對空間環境的判斷。因此, 文章提出了基于兩者結合的天牛群算法(BSO)[12-13]。在BSO算法的迭代過程中，將每個粒子都當作一個個體，并根據PSO的粒子更新規則進行全局搜索。然而，在個體迭代過程中，BSO算法還添加了BAS算法關于天牛個體的更新規則。在每次個體迭代期間，粒子作為個體需要比較其左右兩側的目標函數值, 將目標值更大的一側作為下一次更新群體的位置。BSO算法結合了PSO和BAS兩種算法的優點，能夠更好地提高算法的全局搜索能力，克服了PSO算法容易導致的局部最優、穩定性差等問題。天牛群算法流程如圖2所示，天牛群位置的更新公式如下：

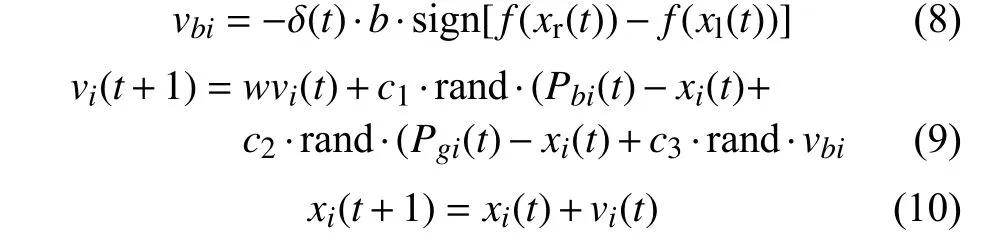
圖2 天牛群算法流程圖

式中：vi(t)——第t次更新后第i個粒子的速度；

xi(t)——第t次更新后第i個粒子的位置；

vbi——粒子的更新速率；

w——慣性因子；

c1、c2、c3——學習因子。

由于學習因子和慣性權重對于PSO和BSO算法的全局和局部搜索能力都具有重要影響，合理的c1、c2、c3以及w取值能夠有效平衡算法的全局和局部搜索能力，可以提升算法的收斂性能，因此，文章對PSO和BSO算法中的學習因子和慣性權重進行改進。

在迭代過程中，對學習因子進行異步變化，從而使得在迭代過程中，開始時自我學習能力較強以便于全局搜索，后期時社會學習能力較強以便于局部搜索，學習因子具體更新規則如下：

式中：c10、c20、c30——對應學習因子的初始值；

a——常數。

經實驗，a取值為1.2最佳。

Shi.Y認為較大的慣性權值有利于全局搜索，較小的慣性權值有利于局部搜索，文章根據Shi.Y提出的線性遞減權重更新規則進行慣性權重規則更新，具體公式如下：

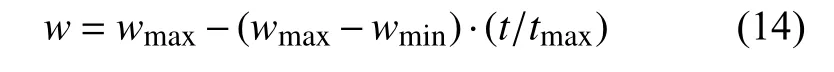
其中wmax、wmin分別為w的最大值和最小值，習慣上取wmax=0.9，wmin=0.4，t為當前更新步數，tmax為最大更新次數。

3.2 基于BSO-BPNN的裝置異常診斷流程

電能計量裝置的異常狀態判斷流程如圖3所示，具體步驟如下：

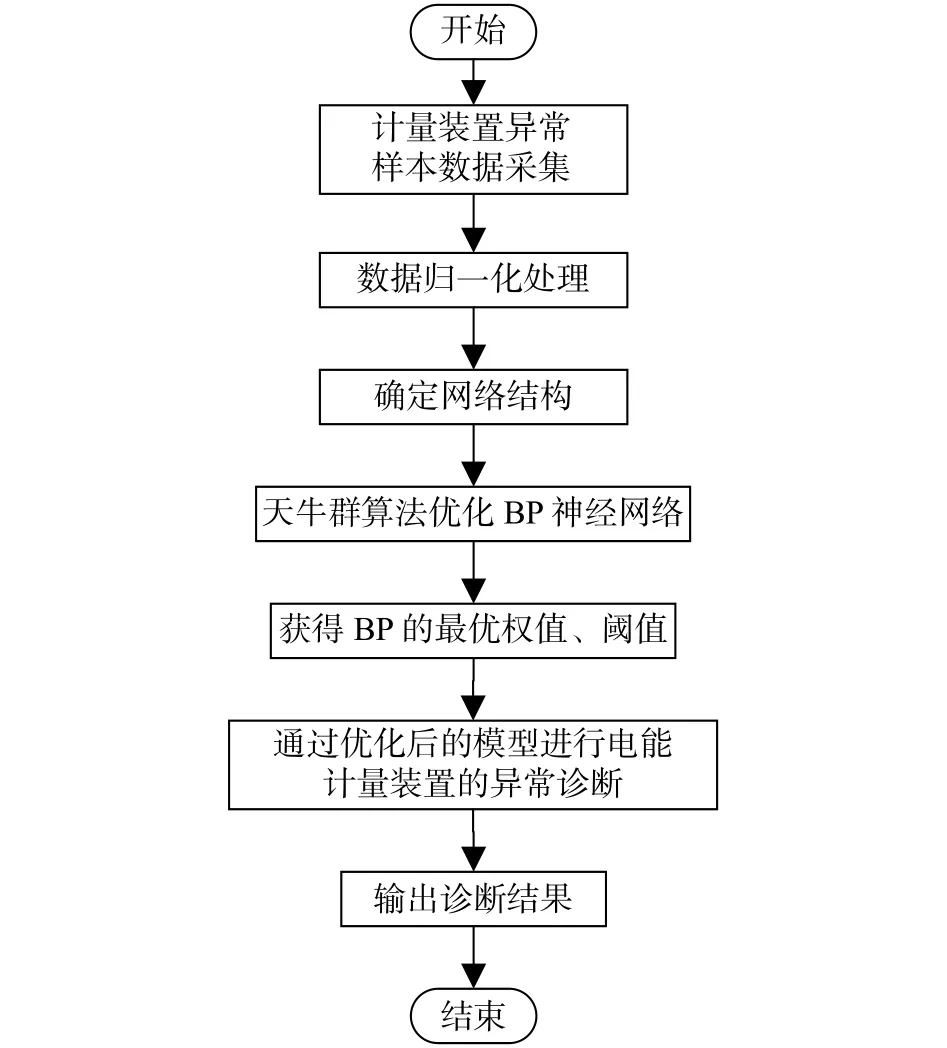
圖3 電能計量裝置異常診斷流程圖

1）根據用電信息采集系統采集到的電能計量裝置巡檢數據，從巡檢表中選擇三相電壓和三相電流數據以及電壓比值和電流比值數據作為BP的訓練樣本，并對數據進行歸一化處理。

2）確定網絡結構。網絡的輸入節點數n=10，隱含層節點數m=12，輸出節點數q=10。

3）初始化粒子群參數。設置天牛群規模N=50，迭代次數t=200，慣性權值w，學習因子初始值c10=1.3、c20=2、c30=3。

4）計算各粒子的目標函數值。以實際輸出類型和預測輸出類型的預測錯誤率作為目標函數，目標函數值最小時，對應權值、閾值的最優解，目標函數表示：

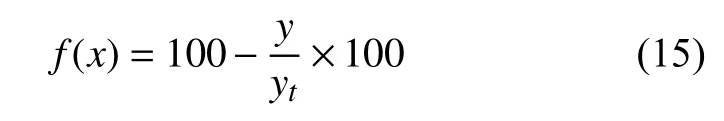
式中：y——預測輸出類型正確個數；

yt——實際輸出類型個數。

5）設置天牛須搜索各參數。δ為迭代步長，左、右須之間距離為d0。

6）根據公式（5）～（7）更新每個天牛的速度和位置。

7）判斷是否滿足天牛須搜索算法的迭代終止條件，若滿足，則繼續下一步驟，若不滿足，則返回步驟6）。

8）根據公式（8）～（14）更新天牛群粒子的速度、位置和權重。

9）判斷是否滿足天牛群算法迭代終止條件，若不滿足，則返回步驟4），直到滿足條件。

10）將種群搜索到的最優粒子作為BP神經網絡模型的初始權值和閾值。

11）利用訓練好的網絡對測試集樣本進行測試，輸出診斷結果。

4 實驗分析

為了驗證BSO-BPNN模型對于計量裝置的異常具有顯著診斷效果。本文利用PSO-BPNN、BSOBPNN和普通BPNN三種模型對計量裝置進行異常診斷實驗，比較三者診斷的準確率以及所需迭代次數。

4.1 數據來源與特征選擇

依據 Q/CSG 113006—2011 《南網普通電子式三相電能表技術規范》[14]、GB/T 15543—2008《電能質量 三相電壓不平衡度》和重慶電網對已有巡檢數據的分析基礎，可以得到電能計量裝置的異常狀態主要與巡檢數據表中裝置的電壓電流值有關。因此文中選擇巡檢數據表中三相三線電能計量裝置的三相電壓值、三相電流值以及電壓比值和電流比值作為數據特征進行分析。文章從重慶地區國家電網采集到的2019年巡檢數據中篩選出458組異常數據和45組正常數據作為樣本數據。在503組樣本中隨機選擇70組數據作為計量裝置異常狀態測試集，其他433組作為計量裝置異常狀態訓練集。文中計量裝置的運行狀態類型以及對應狀態編號如表1所示。

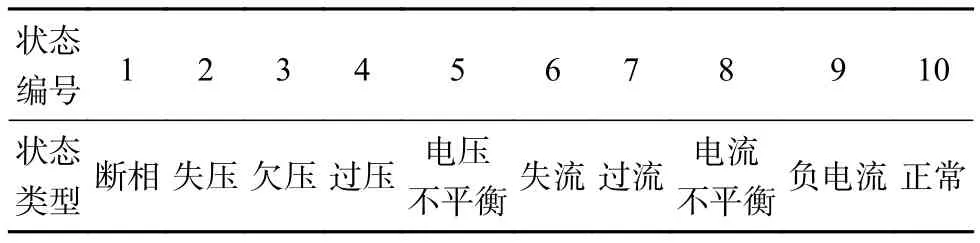
表1 電能計量裝置狀態類型

4.2 實驗結果

利用 PSO-BPNN、BSO-BPNN、BPNN三種模型對電能計量裝置進行異常診斷，診斷結果如圖4～6所示。

圖4 BPNN預測結果對比圖

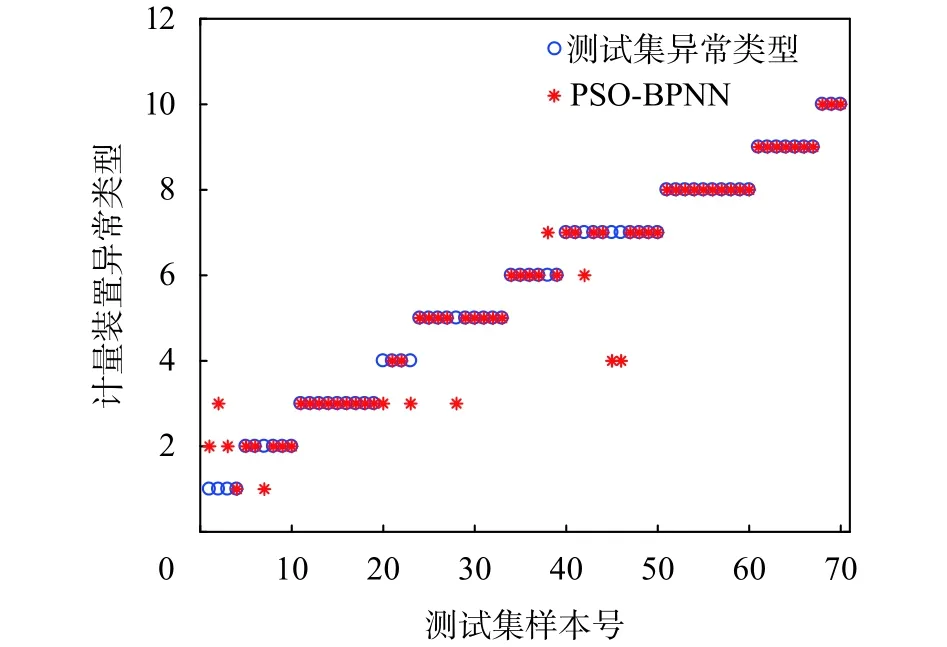
圖5 PSO-BPNN預測結果比對圖

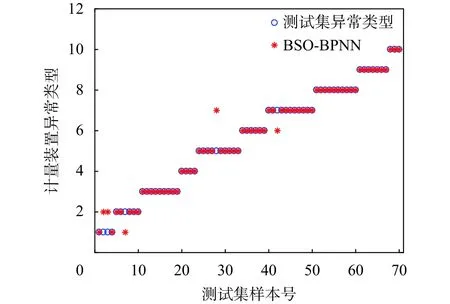
圖6 BSO-BPNN預測結果比對圖

從圖4～6中可以明顯看出，對于電能計量裝置不同狀態的異常診斷，BSO-BPNN模型相比于普通的PSO-BPNN模型和未優化的BPNN模型，具有更高的準確率。

實驗中利用粒子群算法和天牛群算法分別優化BP神經網絡模型得到的迭代曲線如圖7所示。

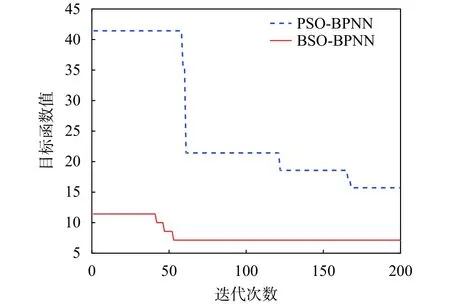
圖7 PSO和BSO迭代曲線對比圖

由圖7可知，單獨的PSO算法所需迭代時間較長，且不易達到穩定，容易陷入局部最優，達到最大迭代次數時的目標值較高。而BSO算法由于在PSO的更新規則中增加了BAS對于個體的更新規則。在初次迭代時，目標值就比較小，而且收斂速度較快，達到穩定需要的迭代次數也較少，說明BSO算法性能明顯由于PSO算法。

表2給出3種模型對于電能計量裝置異常狀態診斷的準確率。由表2可知，PSO-BPNN模型對于計量裝置的異常診斷能力不高，相比于普通BPNN模型沒有明顯優勢。BSO-BPNN模型的診斷準確率最高，該模型對于電能計量裝置的異常診斷能力最強。

表2 3種模型對于裝置異常診斷的準確率

5 結束語

文章以用電信息采集系統采集到的電能計量裝置巡檢數據為基礎，提出了一種基于天牛群優化BP神經網絡的電能計量裝置異常診斷方法。與PSO算法相比，BSO算法結合了PSO和BAS的優點，對于全局和個體的搜索能力都得到了提升。從實驗分析結果可以看出，BSO-BPNN模型的異常診斷準確率達到了92.86%，比PSO-BPNN模型高了8.57%。說明根據電能計量裝置的巡檢數據，使用BSO-BPNN模型對計量裝置進行異常狀態診斷的方法是有效的，為電能計量裝置的異常診斷提供了一種新的方法。