考慮時空相關性的風光出力序列生成方法

李 澤,李鐵成,嚴敬汝,陳天英,郭少飛

(國網河北省電力有限公司電力科學研究院,河北 石家莊 050021)

0 引言

隨著我國“雙碳目標”的提出以及新型電力系統建設進程的不斷推進,以風力發電和光伏發電為代表的新能源將在我國能源系統中發揮越來越重要的作用。但是,風力發電和光伏發電受地理位置和氣候影響較大,具有不確定性和波動性[1-2],其大規模并網必將給電力系統安全穩定運行帶來巨大挑戰。

實際上,同一地區的風光能源在出力上存在一定的相關性[3],充分利用能源之間的相關性并形成聯合調度,可有效克服風光的不確定性帶來的不良影響。目前,關于風光出力的相關性方面已有一些研究。文獻[4]基于非參數核密度估計分別構建了靜態相關系數估計和動態相關系數估計,針對算例數據分別估計相關參數,最后通過擬合優度檢驗和合理性驗證對比了模型刻畫效果,證明了動態相關性模型的合理性及有效性。文獻[5]認為單一模型僅能描述局部相關性,很難適應復雜相關性的建模,為此提出了混合藤Copula模型,并通過算例驗證了所建模型的有效性。文獻[6]運用Spearman相關系數來描述風光之間的出力相關性,再基于神經網絡算法和綜合場景概率法分別得到風電出力和光伏出力,最終生成4組風電出力和1組光伏出力,通過計算光伏與各組風電出力之間的相關性系數來分析風光相關性對無功優化的影響。文獻[1]通過肯德爾秩相關系數反映變量之間的相關性,生成典型風光聯合出力場景。文獻[2]在考慮風光空間相關性的基礎上,提出了考慮風光場站出力時間相關性的建模方法,形成了關于風光多維時空相關性的出力場景。文獻[3]基于非參數核密度估計得到各樣本的邊緣分布函數,隨后根據Frank-Copula將樣本連接起來得到聯合概率分布函數,分時段對分布函數進行采樣,并反變換得到風光出力,最后通過K-means聚類得到典型日場景及對應概率。以上文獻,有的只使用了一種Copula函數來描述風光相關性,未考慮同一地區的風光在不同時段可能存在不同的相關特性,有的通過聚類等方法來獲得風光出力場景,風光出力樣本取自于各時段的風光出力相關性模型,這種方法舍棄了風光出力相關性在時間上的連續,且包含了每天風光場站運行環境情況大致相同的假設,不符合實際情況。

本文提出一種考慮時空相關性的風光出力生成方法。首先,基于動態馬爾科夫鏈方法確定相鄰時刻功率變化的方向和幅值,以此考慮風光出力的時間相關性。然后,基于非參數核密度估計分別對各時刻原始風光出力進行擬合,得到各時刻風光出力的邊緣概率密度函數,并采用Copula函數構建各時刻風光出力的聯合概率分布,以保證風光出力的空間相關性。接著,結合以上方法生成具有時空相關性的風光出力序列。最后,通過算例驗證了本文所提方法的有效性。

1 風光出力相關性理論

1.1 Copula理論

Copula函數最早在1959年由Sklar提出[7-9],常被用于描述多元隨機變量之間的相關性,是一種將各變量的邊緣分布函數連接成聯合分布函數的函數,設多個隨機變量的邊緣分布函數為F1(u1)、F2(u2)、…、F n(u n),其聯合分布函數為H(u1,u2,…,u n),當F1(u1)、F2(u2)、…、F n(u n)連 續時,存在一個唯一確定的Copula函數C滿足

在研究中最常用的Copula函數主要包括兩大類[10-12],橢圓Copula函數和阿基米德Copula函數。橢圓Copula 函數包括Gaussian-Copula,t-Copula等,但由于其具有對稱的尾部相關性,故無法描述非對稱的相關關系。阿基米德Copula函數有著統一的函數表達式,通過調整其中的生成元函數,即可得到不同的阿基米德Copula函數,常見的有Gumbel-Copula,Clayton-Copula,Frank-Copula等。其中,Gumbel-Copula和Clayton-Copula函數分別只對上尾部和下尾部的厚尾特性敏感,而Frank-Copula函數的密度分布呈“U”字形,適合于描述具有對稱厚尾結構變量的耦合關系,且分布比較均勻[13]。因此,本文選用Frank-Copula函數來描述風光出力的空間相關性。Frank-Copula函數如下

式中:u、v為隨機變量;θ為Frank-Copula函數的相關性系數,且θ≠0,當θ＞0時,隨機變量間呈正相關關系,當θ＜0時,隨機變量間呈負相關關系;e為自然常數。

在數學上,常用相關性系數來刻畫2個隨機變量之間的相關性。本文選用Kendall秩相關系數τ,其表達式為

則Frank-Copula函數的相關性系數θ可根據Kendall秩相關系數τ推算

1.2 馬爾科夫鏈

風光出力序列不僅具有空間相關性,還具有時序相關性,即相鄰時刻風光出力在數值大小上呈現一定的規律性[14-15]。而馬爾科夫鏈可通過前面有限個序列確定當前序列的取值,可以很好地描述風光出力的時間相關性。設{X(n),n=0,1,2,…}為狀態空間是參數非負的隨機過程(狀態空間為I),如果{X(n)}滿足

則稱隨機過程{X(n)}為馬爾科夫鏈。式中:P(·|·)為條件概率;k(i n+1|i n)為隨機過程{X(n)}的狀態轉移核。

2 風光出力時空相關性建模

基于常規馬爾科夫鏈方法對風光出力序列采樣,只能求出風光出力序列在各狀態下的概率分布,無法得到確定的風光出力狀態。有研究在這一步采用了馬爾可夫轉移概率最大化法[16],只選取最大轉移概率處的狀態進行計算,這從客觀上摒棄了非最大轉移概率事件發生的可能性,勢必導致計算結果有失全面性。

本文提出動態馬爾科夫鏈采樣方法,將風光出力變化分為若干種狀態,狀態轉移矩陣隨時間而變化,結合各時刻狀態轉移矩陣和各狀態出力變化范圍,計算出下一時刻的出力期望值。

通過分析河北省南部電網某地區2個位置相鄰風電場和光伏電站的實際出力序列,發現在有效觀測區間內,風電場出力Pw和光伏電站出力Ps在t+1時刻的出力狀態均與其在t時刻的狀態不同,即Pw,t≠Pw,t+1,Ps,t≠Ps,t+1。因此,假設t時刻風光出力序列為P t,則有P t={Pw,t,Ps,t},對于t+1時刻,P t有4種可能的轉移狀態,分別為風光出力均增大、風出力增大光出力減小、風出力減小光出力增大和風光出力均減小,將其發生概率分別設為k t_t+1,i(i=1,2,3,4)。

對于t時刻到t+1時刻的風光出力狀態轉移矩陣,即K t_t+1有

以t時刻出力條件下,t+1時刻風光出力均增大的情況為例。基于風光出力序列樣本,計算t時刻到下一時刻風光同時增加的情況頻數m t_t+1,1,t時刻總的樣本數量記為M t_t+1,1,則有

同時,計算風光出力增大比例的最大值和最小值,分別記為nw,1,max|t_t+1、nw,1,min|t_t+1和ns,1,max|t_t+1、ns,1,min|t_t+1。為了簡化計算,在此將各狀態下風光各自出力變化情況看作線性變化,則t+1時刻風電在風光出力均增大時的出力期望值為

重復上述步驟得到t時刻下4個狀態期望值,再通過加權計算可得t+1時刻的風光出力期望值。

3 風光出力序列生成步驟

風光出力序列生成步驟如下:

(1)生成2個在(0,1)上服從均勻分布的隨機數作為風光出力序列初始值,分別記作Pw,1、Ps,1;

(2)基于風光出力序列樣本計算從當前時刻到下一時刻的轉移概率矩陣K t_t+1;

(3)分別計算下一時刻各狀態出力變化比例的最大值和最小值,結合式(8)、式(9)計算各狀態出力期望值其中j表示所屬轉移狀態,j=1,2,3,4;

(4)對步驟(3)所得各狀態出力期望值進行加權計算得下一時刻風光出力期望值,權重為各狀態對應的轉移概率k t_t+1,j,則有

(5)根據式(3)、式(4)計算t+1時刻風光出力序列得到對應Frank-Copula函數的參數θt+1;

(6)計算參數為θt+1的Frank-Copula函數C(u,v)在附近的解,并取歐氏距離最小者作為t+1時刻風光出力計算值Pw,t+1和Ps,t+1;

(7)重復步驟(2)—(6),直至風光出力序列生成數滿足要求。

4 算例分析

4.1 樣本數據

以河北省南部電網某地區2個位置臨近的風電場和光伏電站7—8月連續30 d的出力數據為樣本。表1為根據樣本求得的風光出力的均值、中位數及方差。風電場容量為150 MW,光伏電站容量為200 MW,實際計算時均采用風光出力的標幺值,統計區間為每天06:00—18:00時間段,數據采樣間隔為5 min,風電場出力記為Pw,光伏電站出力記為Ps。圖1為原始數據對應的風光出力序列散點示意。

表1 風光出力統計特征

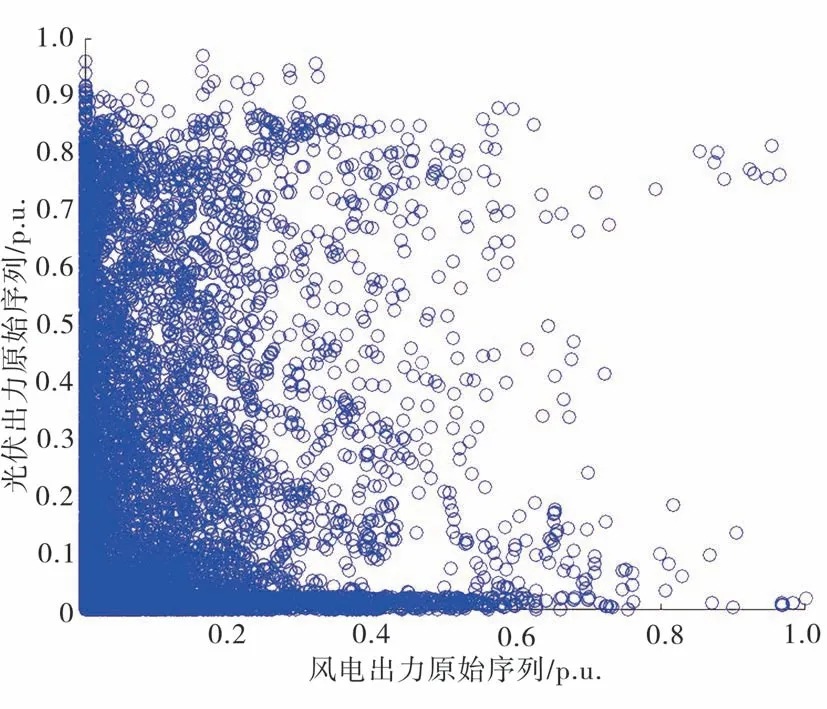
圖1 原始風光出力散點示意

4.2 Frank-Copula模型參數估計

采用非參數核密度估計法確定風光出力的邊緣概率分布函數F(Pw)和F(Ps)。對某一變量X={X i},i=1,2,…,n,其概率密度函數的核估計為[17-18]

式中:n為樣本數量;K(x)為核函數,本文取高斯函數;h為帶寬系數,其值選擇將影響對X i的擬合準確度,本文根據最優帶寬經驗公式進行求解[19],如式(13)所示。對進行積分即可得到風光出力的邊緣概率分布。

圖2給出了Pw和Ps經驗分布曲線和核分布估計曲線。由圖2可看出,采用非參數核分布估計得到的樣本擬合結果,可以很好地描述風光出力的數據特征,且光滑度更好。

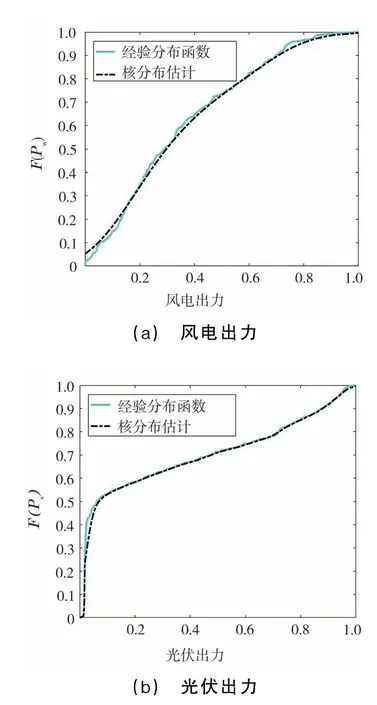
圖2 風光出力分布曲線對比

基于非參數核分布估計法對每個時刻的風光出力數據進行擬合,再根據式(3)、式(4)分別計算風、光同一時刻的相關性系數,最終由式(2)得到相應的Frank-Copula模型。以第84個時刻為例,表2給出了該時刻風、光出力概率密度函數的帶寬系數及Frank-Copula模型的相關性系數,圖3(a)為Frank-Copula函數擬合的風光出力密度函數,圖3(b)為擬合的風光出力分布函數。

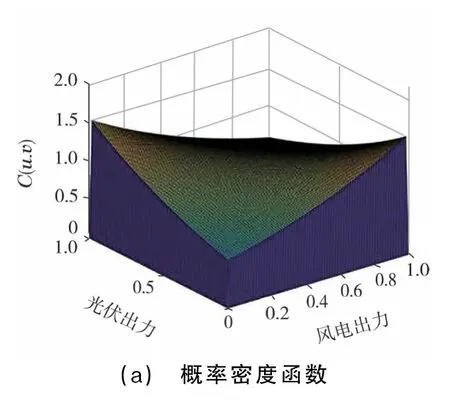
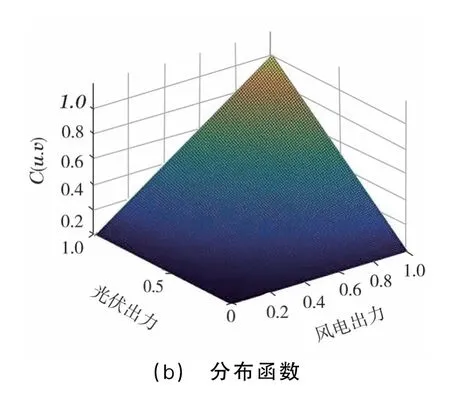
圖3 第84個時刻擬合值的概率密度及分布情況

表2 第84個時刻的帶寬系數及相關性系數

4.3 方法驗證

根據第3節步驟生成風光出力序列,圖4為按照本文方法擬合得到的風光出力時序圖。將風光出力的原始數據分別按時刻劃分求取平均值,可得風光原始出力的整體變化情況,如圖5所示。在風光原始數據中,分別尋找與擬合風光出力之間歐氏距離最小的風電和光伏出力序列,結果為第27天風光出力均最接近擬合結果,此時風電出力實際值與擬合值之間歐氏距離為1.094 4,光伏出力的歐氏距離為1.429 8,第27天風光實際出力情況如圖6所示。

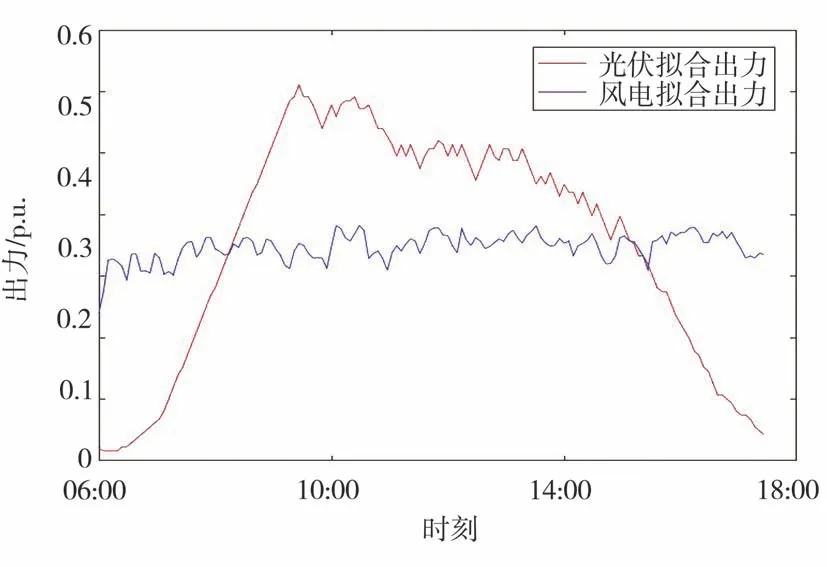
圖4 風光出力序列擬合情況

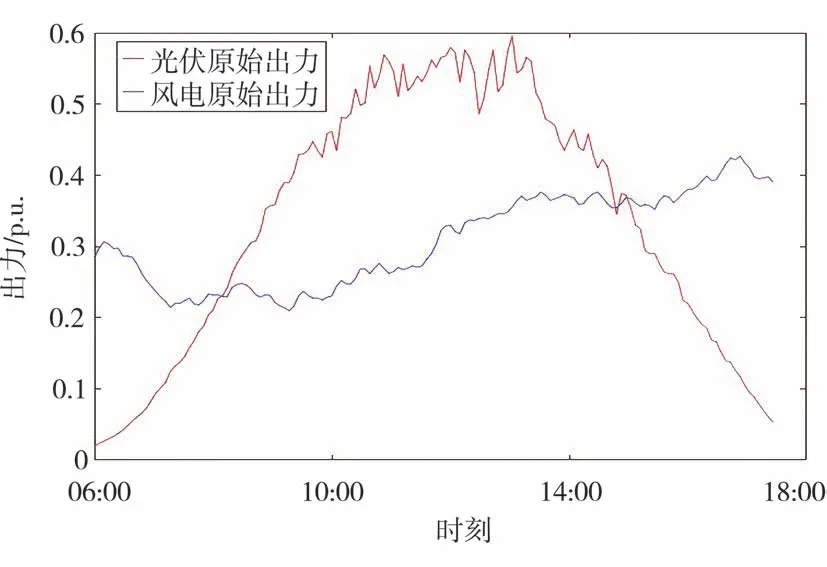
圖5 風光原始出力情況

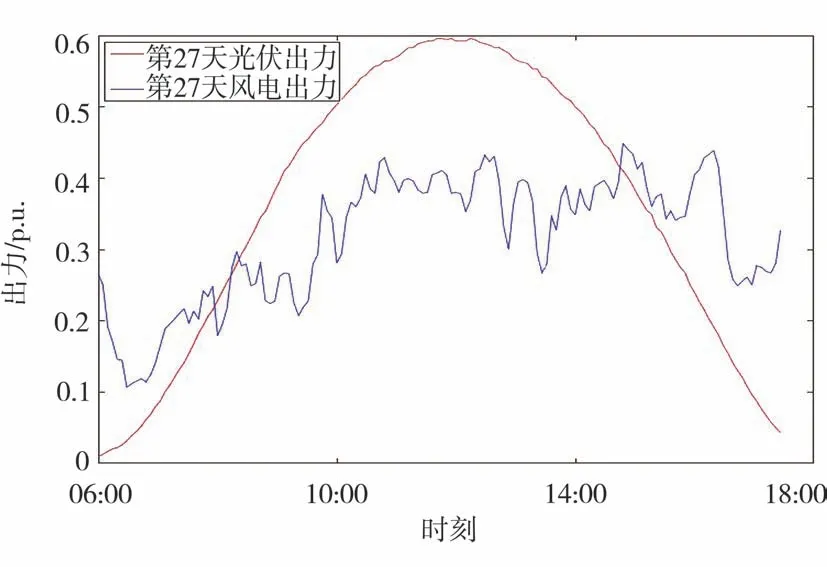
圖6 第27天風光出力情況

對比圖4-6可以看出,擬合結果基本保留了原始樣本的數據特征,同時也具有一定的隨機性。在06:00—10:00,擬合結果中光伏出力逐漸增大,風電出力則在波動中逐步下降,這與原始樣本的出力變化趨勢相符。而這段時期光伏擬合出力較原始出力增大更快,這是由于原始樣本中存在部分數據點前期光伏出力為0,導致通過平均求得的光伏原始出力變化率減小。

由圖6可以看出,原始樣本中存在光伏起始增大較快的情況,故本文方法較好地兼顧了樣本整體與個體的數據特征。在10:00—12:00,擬合結果中光伏出力先是下降,然后維持在較大出力位置,與原始樣本中光伏出力持續在最大出力附近波動不同,這是因為光伏電站在正常運行時,有時會因白云遮擋陽光導致出力下降,而原始樣本出力因為求和平均的算法使得該數據特征被抹去,擬合結果中的光伏出力就是將這種隨機性體現了出來。在12:00—18:00,擬合結果中光伏出力逐漸下降,風電出力隨之升高,與原始樣本的出力變化情況一致。整體來看,擬合結果中的風電出力較原始樣本平均出力波動范圍要大,更符合實際運行情況。

為進一步驗證本文方法的實用性,以天為單位對原始樣本進行分類,形成代表風光出力大、中、小的3種運行情況,并分別將其所包含數據定義為第1組、第2組和第3組,各類運行情況相關信息如表3所示,采用第3節方法分別對3組數據進行仿真模擬,模擬結果的統計數據如表4所示。

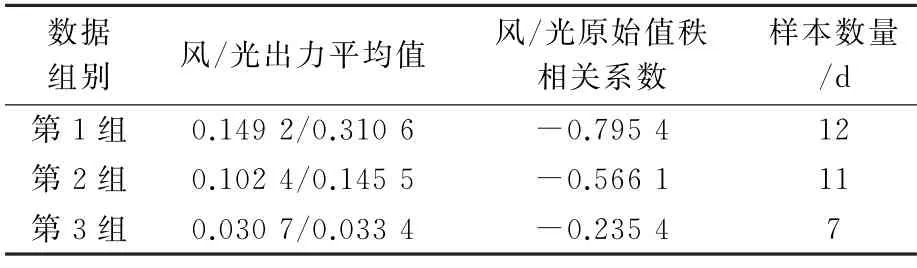
表3 風光出力運行情況分類結果

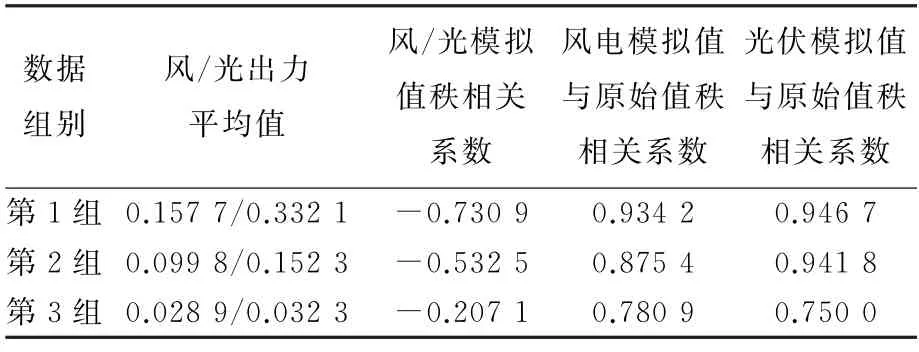
表4 各類風光出力運行情況模擬結果

統計數據顯示,根據本文所提方法得到的模擬結果很好的保持了樣本數據的均值特征,誤差均不超過7%。模擬結果中,風光出力最大時其秩相關系數為負且幅值也最大,代表其負相關屬性較強;當風光出力最小時,負相關屬性最弱,這與原始數據的特征一致,說明本文方法很好地保持了風光出力的空間相關性。分別計算模擬結果中風光出力與原始數據中風光出力的秩相關系數,可以發現其正相關性屬性較強,最大為0.946 7,最小為0.750 0,說明本文方法能夠模擬風光出力各自的變化趨勢,較好地保留了風光出力的時間相關性。從表4數據進一步可以看出,隨著出力水平的降低,風光模擬結果與原始數據的秩相關系數也在逐漸減小。其原因:一是樣本數量逐步減少,隨之帶來的誤差增大;二是隨著風光出力水平下降,其出力的隨機性和波動性進一步增強,引起模型計算的偏差增大,導致變量之間的相關性降低。

4.4 適應性分析

提取風電場和光伏電站第31天的實際出力數據,并將其與擬合結果進行對比,如圖7、圖8 所示。由圖7和圖8可以看出,在06:00—10:00,風光實際出力與擬合結果吻合度較高。隨后風電實際出力驟升,超過擬合結果預測值,此時光伏實際出力則持續波動,始終在擬合結果附近震蕩。該情況持續到15:00左右,風電實際出力突然大幅下降跌至擬合結果預測值以下,而光伏實際出力則恢復與擬合結果較高的吻合水平。通過查詢天氣數據,當天地區發布大風黃色預警。由此可以推測,10:00—15:00的數據波動為短時極端強對流天氣所致,而此類隨機影響難以從風光歷史出力數據中提取并分析[20-21],因此導致部分時段預測值誤差較大。表5給出了風光預測出力水平和第31天實際值的對比情況。

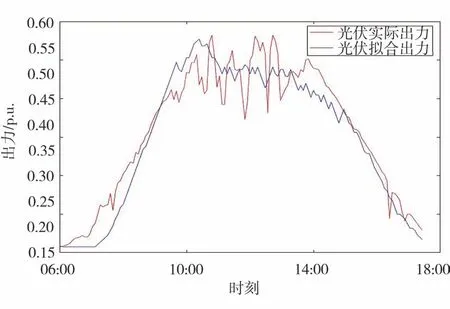
圖7 第31天風電實際出力與擬合結果對比

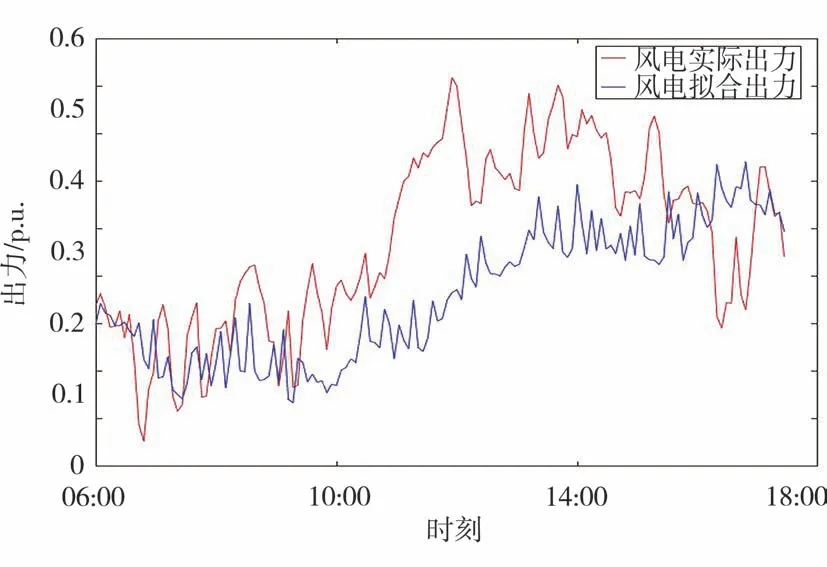
圖8 第31天光伏實際出力與擬合結果對比

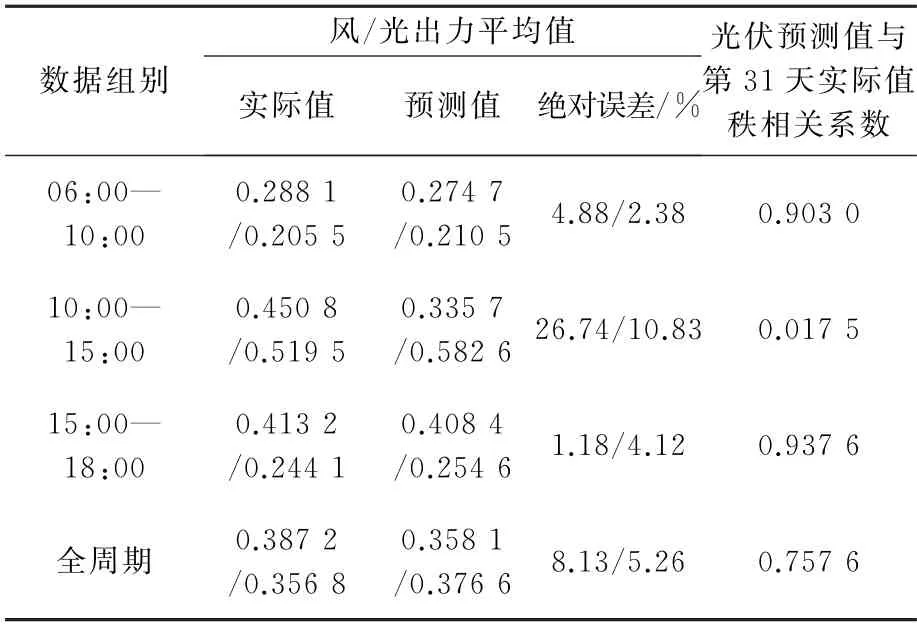
表5 風光出力情況對比

為了更直觀對比,將觀測周期按照該文分析結果劃分為3個階段。通過表5比較可知,全周期內,風光預測誤差分別為8.13%和5.26%,在可接受范圍內。其中,06:00—10:00 以及15:00—18:00風光預測平均值與實際平均值相差極小,誤差均在5%以下,體現了本文方法在天氣穩定情況下較好的準確性。10:00—15:00,預測出現較大誤差,且風電出力誤差超過25%。一方面,證明了短時極端天氣變化難以預測,模型在該問題上仍有待完善,另一方面,某些極端天氣變化對風電的影響要遠大于對光伏的影響,這在今后的研究中應著重考慮。相關性方面,以光伏為例,全周期秩相關系數為0.757 6,證明模型較好地模擬了光伏出力變化趨勢。其中,06:00—10:00、15:00—18:00 模擬結果尤為出色,秩相關系數均在0.900 0以上。

5 結論

本文從風光出力序列的時間相關性和空間相關性2個角度出發,基于Frank-Copula函數和動態馬爾科夫鏈采樣,建立了考慮時空相關性的風光出力模型,提出了一種新的風光出力序列生成方法。通過算例驗證得出以下結論。

(1)與常規采樣方法抹去了變量的時序特征不同,基于本文提出的動態馬爾科夫鏈進行采樣,結果既能反映變量的概率分布,又能夠維持變量的時序特征,再現變量自身的時間相關性。

(2)Frank-Copula函數能夠模擬變量間的相關性,尤其是對于具有負相關性的風光出力模型,Frank-Copula函數能夠很好地展示地理位置和地形環境帶來的空間相關性。

(3)本文方法在天氣穩定情況下能夠較好地模擬風光出力的變化趨勢。短時極端強對流天氣是風光出力預測的一個重要影響因素,尤其對風電出力的影響往往更大,這在今后的研究中仍有待完善。相關性風光出力模擬能夠為電力系統經濟調度及新能源規劃提供數據基礎,把模擬得到的計及時空相關性的風光出力序列應用到新能源高滲透率電力系統中以提升電能質量和優化運行,將是下一步的研究工作。