智慧校園供水系統(tǒng)的可視化及其關(guān)系模型的構(gòu)建
陳培輝 石慧 李掀金









摘? 要: 智慧校園供水系統(tǒng)是智慧校園的重要組成,為了提升智慧校園的服務(wù)和管理水平,文章就供水系統(tǒng)的用水可視化及用水量預(yù)測這兩個(gè)問題展開分析和研究。利用可視化技術(shù)和回歸模型對校園供水情況進(jìn)行深入挖掘和分析,為智慧校園供水系統(tǒng)的智能化管理提供更多的信息和幫助。
關(guān)鍵詞: 智慧校園供水系統(tǒng); 數(shù)據(jù)分析; 可視化; 回歸模型
中圖分類號(hào):TP399? ? ? ? ? 文獻(xiàn)標(biāo)識(shí)碼:A? ? ?文章編號(hào):1006-8228(2022)02-42-05
The visualization of the intelligent campus water supply system and
the construction of its relational model
Chen Peihui, Shi Hui, Li Xianjin
(Faculty of Engineering, Shanwei Institute of Technology, Shanwei, Guangdong 516600, China)
Abstract: Smart campus water supply system is an important part of the smart campus. In order to improve the service and management level of smart campus, this paper analyzes and studies the water visualization and water consumption prediction of water supply system. The visualization technology and regression model are used to deeply excavate and analyze the campus water supply situation, so as to provide more information and help for the intelligent management of the intelligent campus water supply system.
Key words: smart campus water supply system; data analysis; visualization; regression model
0 引言
智慧城市是當(dāng)下現(xiàn)代化城市進(jìn)程中的一個(gè)重要環(huán)節(jié),通過建設(shè)智慧城市,能夠更好的提高人民日常生活水平、質(zhì)量和標(biāo)準(zhǔn)[1]。智慧校園作為智慧城市中的重要元素之一,實(shí)現(xiàn)供水系統(tǒng)的智能化管理是實(shí)現(xiàn)智慧校園的重要任務(wù)之一,而隨著智能水表在校園的逐漸普及,對智能水表所提供的實(shí)時(shí)運(yùn)行數(shù)據(jù)進(jìn)行分析處理,為提升智慧校園的服務(wù)和管理水平創(chuàng)造了良好的機(jī)會(huì)[2-3]。
智慧校園供水系統(tǒng)的分析處理涉及數(shù)據(jù)預(yù)處理、數(shù)據(jù)可視化、數(shù)據(jù)建模等一系列大數(shù)據(jù)技術(shù)。可視化技術(shù)在當(dāng)前發(fā)展正趨于成熟,應(yīng)用可視化技術(shù)對預(yù)處理后的水表數(shù)據(jù)構(gòu)建各水表和學(xué)校功能區(qū)的用水可視化體系,能夠?yàn)橹腔坌@供水系統(tǒng)的管理提供更為直觀的用水情況。而用水量的預(yù)測是智慧校園供水系統(tǒng)的另一項(xiàng)重要任務(wù)。供水系統(tǒng)的運(yùn)行數(shù)據(jù)是數(shù)值型數(shù)據(jù),針對該類數(shù)據(jù)可采用回歸模型,結(jié)合校區(qū)水表層級關(guān)系,建立層級水表數(shù)據(jù)之間的關(guān)系模型,形式化水表的運(yùn)行模式,為智慧校園供水用水進(jìn)一步提供有力的決策支撐[4]。
有效地利用可視化技術(shù)和回歸模型對校園供水情況進(jìn)行深入挖掘和分析,能夠?yàn)橹腔坌@供水系統(tǒng)的智能化管理提供更多有效的信息和幫助。
1 研究分析
本文采用的數(shù)據(jù)是來自2020年全國高校數(shù)學(xué)建模競賽的比賽數(shù)據(jù),該數(shù)據(jù)為某高校的校園供水實(shí)時(shí)數(shù)據(jù),包括多個(gè)附件。該比賽數(shù)據(jù)的特點(diǎn)是數(shù)據(jù)量大、具有層級關(guān)系、且以一定的時(shí)間間隔提供相應(yīng)的用水?dāng)?shù)據(jù)。本文主要針對供水系統(tǒng)的用水可視化及用水量預(yù)測這兩個(gè)問題展開分析和研究。
1.1 針對用水可視化的分析
要求利用已知各個(gè)水表的數(shù)據(jù)進(jìn)行統(tǒng)計(jì)、分析得到變化規(guī)律,劃分功能區(qū)得到各功能區(qū)的用水特征。
首先,利用python的Pandas庫將數(shù)據(jù)以四個(gè)小時(shí)為一段時(shí)間整合成以天為單位統(tǒng)計(jì),并歸納劃分成為四個(gè)季度圖表,以便后續(xù)的計(jì)算與描述;其次,利用Excel根據(jù)以區(qū)域?yàn)榫S度劃分出具有代表性的六大功能區(qū),考慮到水表層級關(guān)系數(shù)據(jù)有極少的空白值,對這部分?jǐn)?shù)據(jù)采取剔除處理。
數(shù)據(jù)預(yù)處理后,根據(jù)所得到的數(shù)據(jù)繪制季度圖表與功能區(qū)圖表,分析得到各個(gè)水表的變化規(guī)律;然后,對圖表信息進(jìn)行充分的挖掘與分析,計(jì)算出功能區(qū)用水的峰值與落差;最后,依據(jù)數(shù)據(jù)給出六大功能區(qū)的用水特征。
1.2 針對關(guān)系模型的分析
要求結(jié)合水表的層級關(guān)系建立關(guān)系模型并分析模型誤差,從而可用于預(yù)測用水量。
該問題的出發(fā)點(diǎn)是利用層級關(guān)系與水表數(shù)據(jù)構(gòu)建不同層級水表的關(guān)系模型,問題的本質(zhì)是數(shù)值型預(yù)測任務(wù)。因此,可通過構(gòu)建層級關(guān)系與水表數(shù)據(jù)的多元回歸關(guān)系模型,用于預(yù)測用水量。至此,本文的思路是嘗試建立相應(yīng)的回歸模型,對數(shù)值進(jìn)行預(yù)測,并與真實(shí)水表數(shù)值進(jìn)行對比,檢測模型的準(zhǔn)確率。
2 用水可視化
2.1 數(shù)據(jù)探索性分析
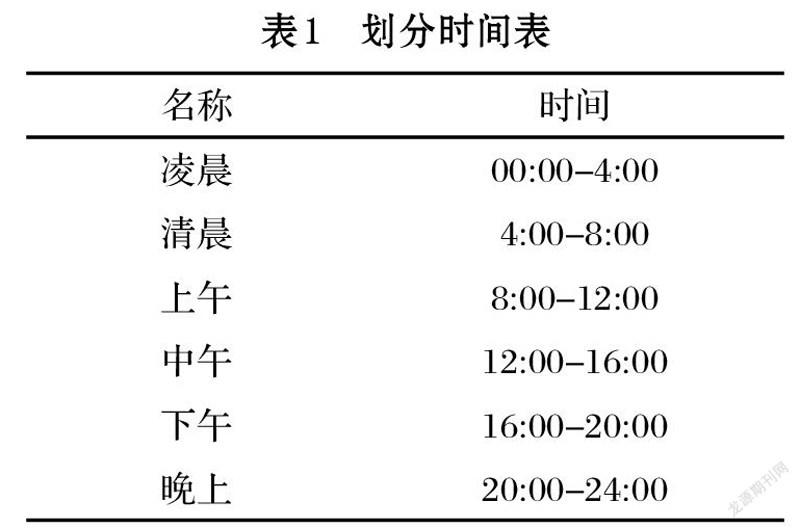
基于該供水系統(tǒng)的智能水表所提供的用水?dāng)?shù)據(jù)以及水表層級關(guān)系數(shù)據(jù),本文將一天以四個(gè)小時(shí)為粒度劃分為六大時(shí)間段,以便后續(xù)的計(jì)算與描述。如表1所示。
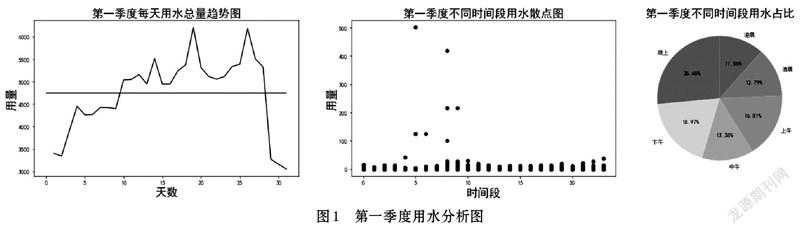
接下來,在劃分時(shí)間段基礎(chǔ)上,整合四個(gè)季度的用水分析圖,繪制出圖表,如圖1~圖4所示。
由圖1可知:①在第一季度中,每天的用水量總體呈上升趨勢,但整體用水量較小,在月上旬至中旬用水量隨著天數(shù)在4000-6000(立方米)持續(xù)增長,并在月中下旬(15-25日左右)達(dá)到6000(立方米)峰值;②不同時(shí)間段用水較為平衡。
由圖2可知:①在第二季度中,每天的用水量總體呈上升趨勢,整體用水量大,在月上旬至中旬用水量整體在6000-8000(立方米)平緩增長,在月中下旬20-25日達(dá)到18000(立方米)峰值;②不同時(shí)間段用水差異較大,晚上用水占比大為28.1%,達(dá)到最高峰,凌晨為低峰期。
由圖3可知:①在第三季度中,每天的用水量總體變化較大,在7000-10000(立方米)波動(dòng),在月上旬至中旬用水量較少,月中下旬23日為10000(立方米)峰值;②不同時(shí)間段用水較均衡,晚上用水占比大為27.1%最高峰,其余時(shí)間較為平衡。
由圖4可知:①在第四季度中,每天的用水量總體平緩,整月總量變化較小;②在下午與晚上用水較多,其余時(shí)間段用水差異較為平衡。
2.2 功能區(qū)求其用水特征
根據(jù)智能水表提供的數(shù)據(jù),對其進(jìn)行歸類劃分,可得該校園供水系統(tǒng)具有代表性的六大功能區(qū),分別為:辦公樓、教學(xué)樓、宿舍、食堂、運(yùn)動(dòng)區(qū)、休閑區(qū);其次,為了清晰地對比不同功能區(qū)在每天的用水需求量,通過匯總各功能區(qū)每天的用水?dāng)?shù)據(jù),進(jìn)行均值處理,采用折線圖刻畫其用水規(guī)律。結(jié)果如圖5所示。
由不同功能區(qū)用水時(shí)間變化圖5可知:
⑴ 辦公樓的用水特征是波動(dòng)上升,在清晨至上午平緩上升幅度較大,到中午有下落而后持續(xù)上升;
⑵ 宿舍的用水特征是平緩上升,凌晨持續(xù)至中午平穩(wěn),由中午到晚上呈平緩上升;
⑶ 教學(xué)樓、食堂、運(yùn)動(dòng)區(qū)、休閑區(qū)的用水特征是趨于平和,在上午和下午有輕微浮動(dòng)。
3 構(gòu)建關(guān)系模型
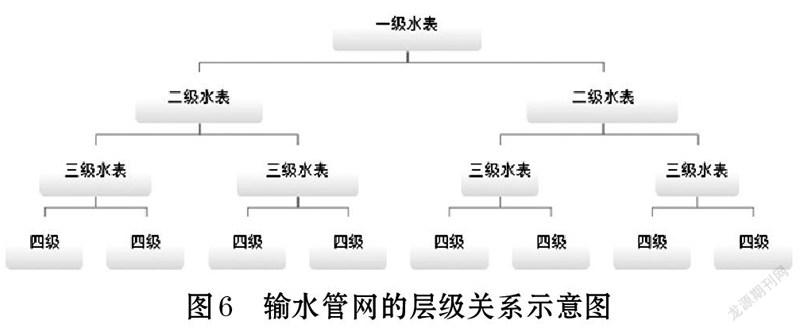
在構(gòu)建不同層級水表的關(guān)系模型上,首先,分析水表的層級關(guān)系問題,刻畫層級關(guān)系結(jié)構(gòu);其次,通過構(gòu)建逐層級的水表關(guān)系模型,預(yù)測不同層級水表的用水量,并進(jìn)行誤差檢驗(yàn)。
3.1 數(shù)據(jù)的預(yù)處理
首先,利用Python的Pandas庫對四個(gè)季度的水表層級數(shù)據(jù)進(jìn)行聚合,得出各級水表的用水量總和,如表2所示。其次,考慮到月份的天數(shù)差異,采取合理的方式對異常值取平均值的處理;最后,基于回歸模型,構(gòu)建逐層級的多元回歸關(guān)系模型,并檢驗(yàn)?zāi)P蛿M合度。
3.2 建立關(guān)系模型
首先,以每月的日期為自變量,用水量為因變量,根據(jù)表2的數(shù)據(jù)結(jié)果,將數(shù)據(jù)導(dǎo)入Pandas庫、Numpy庫、Matplotlib庫,建立起四個(gè)關(guān)于水表層級的多元回歸關(guān)系模型,最后對各個(gè)模型進(jìn)行檢驗(yàn)。
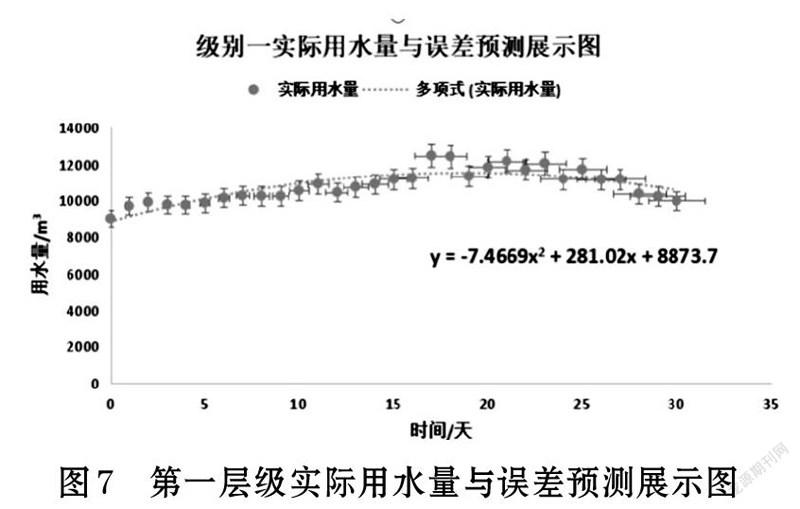
第一層級的線性回歸擬合模型關(guān)系式為:
y=-7.4669x+281.02x+8873.7
第二層級的線性回歸擬合模型關(guān)系式為:
y=-10.194x+451.94x+9627.3
第三層級的線性回歸擬合模型關(guān)系式為:
y=-3.1056x+91.704x+3271.6
第四層級的線性回歸擬合模型關(guān)系式為:
y=-0.483x+15.797x+386.2
利用R值對不同層級的關(guān)系模型進(jìn)行檢驗(yàn),結(jié)果如表3所示。
R的取值范圍為-1到1之間,即-1≤R≤1,當(dāng)R越趨近于1或-1時(shí),代表模型擬合越好,當(dāng)R越趨近于0時(shí),代表模型擬合越差。
由表3結(jié)果可知:
⑴ 第一、第三、第四層級的關(guān)系模型擬合良好;
⑵ 第二層級關(guān)系模型的[R2]值較低,究其原因是存在少量異常的離異點(diǎn),結(jié)合圖形來綜合分析,實(shí)際上第二層級水表關(guān)系模型擬合度良好。
綜上,四個(gè)層級的關(guān)系模型擬合較好。
4 結(jié)論
本文針對智慧校園供水系統(tǒng)的用水可視化和用水量預(yù)測問題,利用數(shù)據(jù)探索性分析方法和多元回歸模型,進(jìn)行充分的信息挖掘,針對用水可視化問題,得到不同時(shí)段和不同功能區(qū)的用水規(guī)律,針對用水量預(yù)測問題,構(gòu)建逐層級的關(guān)系模型,可用于預(yù)測不同層級水表的用水量。
智慧校園供水系統(tǒng)的智能化囊括多個(gè)方面,未來還需研究智慧校園供水系統(tǒng)的明漏與暗漏的檢測和定位,進(jìn)一步提升智慧校園的服務(wù)和管理水平。
參考文獻(xiàn)(References):
[1] 朱磊.智慧城市與大數(shù)據(jù)在城市規(guī)劃中的應(yīng)用[J].中國科技信息,2021,4(14):39-40
[2] 梁濤,韓超,張志果.建設(shè)智慧供水全流程監(jiān)管“一張網(wǎng)”的思考[J].給水排水,2020,56(6):157-162
[3] 薛毅.“校園供水系統(tǒng)智能管理”的問題解析[J].數(shù)學(xué)建模及其應(yīng)用,2021,10(1):101-111
[4] 韓中庚.數(shù)學(xué)建模方法及其運(yùn)用[M].高等教育出版社,2004

