基于區分對的混合型弱標記數據增量約簡算法

金 莎， 鄭穎春

(西安科技大學 理學院，陜西 西安 710600)

0 引言

粗糙集理論是由波蘭學者Pawlak提出的[1]，屬性約簡[2]是其重點研究內容，用于降低原始數據集維數, 剔除數據集的冗余和不相關屬性。目前，基于信息系統[3-9]和決策系統[10-16]中的屬性約簡算法研究較多。

已有的屬性約簡算法只能解決有標記數據或無標記數據的約簡問題，現實中因數據采集需要消耗大量成本或受技術限制，導致得到的數據大多是缺失、無標記的。文獻[17]定義不完備弱標記數據的半監督差別矩陣，利用基于協同學習的思想將無標記的數據中信度較大的數據轉換為有標記數據。文獻[18]提出了一種半監督特征選擇算法，該算法通過組合半監督散點，有效利用大量未標記的視頻數據中的信息來區分目標類別。文獻[19]針對弱標記的符號型數據，利用半監督學習框架，構造相對應的啟發式半監督屬性約簡算法，然而該算法是非增量的，運行效率較低。文獻[20]采用鄰域粗糙集對部分標記數據進行屬性約簡，結合兩種不同的度量方法得到綜合重要性并設計啟發式算法進行約簡計算。文獻[21]在粒計算的背景下提出不完備弱標記決策系統中的區分對定義，基于半監督學習給出決策系統中樣本增加或減少的增量屬性約簡算法，然而并沒有給出樣本變化時的增量機制。

上述算法在處理動態變化的弱標記數據屬性約簡問題時，需要不斷重復大量計算，沒有相應的增量機制，計算復雜度高，分類性能低，且大多只能處理符號型數據。故針對混合不完備、且數據存在缺失的動態變化數據集，本文給出區分關系的更新定理，建立屬性動態變化的增量機制,并提出相應的增量屬性約簡算法。最后，通過實驗分析了本文增量屬性約簡算法與文獻[19]、文獻[20]中屬性約簡算法的計算效率和分類性能。

1 預備知識

文獻[21]中指出，弱標記數據是既含有有標記的數據也包含無標記數據的集合。若混合型決策系統的決策屬性值d存在缺失(即類別無標注)，則稱這是一個混合型弱標記決策系統。

定義1 給定混合型弱標記決策系統TS=〈U=L∪N,C∪D,V,f〉， 其中，U是包含所有樣本的非空有限集合，L是包含所有有標記樣本的集合，N是包含所有無標記樣本的集合，這里C=Cd∪Cr，Cd為離散型屬性集，Cr為連續型屬性集，D為決策屬性集，對于?a∈C，定義屬性a的區分關系DISC(a,U2)為：

DISC(a,L2)={(xi,xj)|(a∈Cd,f(a,xi)≠f(a,xj))∨(a∈Cr,f(a,xi)-f(a,xj)|<δ)∧

(1)

DISC(a,N2)={(xi,xj):(a∈Cd,f(a,xi)≠f(a,xj))∨(a∈Cr,f(a,xi)-f(a,xj)|<δ)∧

f(a,xi)≠*∧f(a,xj)≠*,xi,xj∈N}；

(2)

DISC(a,U2)=DISC(a,L2)∪DISC(a,N2)，

(3)

性質1 對于混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，設屬性集B?C，則屬性集的區分關系一定滿足：

DISC(B,U2)?DISC(C,U2)。

(4)

證明根據區分關系定義1可知，對于?B?C，總是存在a∈C-B，DISC(a,L2)≠φ或DISC(a,N2)≠φ，所以有DISC(a,U2)=DISC(a,L2)∪DISC(a,N2)≠φ，滿足|DISC(a,U2)|≥0， 因此DISC(B,U2)?DISC(C,U2)成立。性質1證畢。

定義2[21]給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，對?B?C，若B的區分關系滿足以下兩個條件，則稱B為混合型弱標記決策系統的約簡，記為redC：

(Ⅰ)DISC(C，U2)=DISC(B,U2)；

(Ⅱ)對?a∈B，有DISC(B，U2)≠DISC(B-{a}，U2)。

2 混合型弱標記數據的非增量約簡算法

根據區分關系定義，DISC(C,U2)表示屬性集C所區分的論域U×U中所有樣本對的集合，根據定義2，若DISC(C,U2)=DISC(B,U2)成立，B就是屬性約簡集，由性質1得DISC(B,U2)?DISC(C,U2)總是成立的，因此計算屬性約簡時，為減少要識別的樣本對，可以將原本要區分的樣本對U×U改為DISC(C,U2)，若屬性集B能辨別屬性集C所區分的所有樣本對，它就是這個決策系統的屬性約簡。基于上述思想，本文構造了一種面對混合型弱標記不完備決策系統的屬性相對區分度計算公式。它能與反向刪除思想結合，不斷去掉當前已能區分的區分對，逐步減少所要識別的區分對數量。

定義3 給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，對?a∈C，定義屬性相對區分度為：

(5)

表示屬性a相對于屬性集C能區分的樣本對個數所占比例。

性質2 對于混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，若屬性集B?C，則有DISC(C-B,U2)≠DISC(C,U2)-DISC(B,U2)。

證明假設屬性集B是屬性集C的約簡，且B是包含于C的，根據定義2，它們的區分關系滿足DISC(C,U2)=DISC(B,U2)，則DISC(C,U2)-DISC(B,U2)=0。對a∈C-B，一定存在a使得DISC(a,U2)≠0成立，得DISC(C-B,U2)≠0，所以DISC(C-B,U2)≠DISC(C,U2)-DISC(B,U2)。性質2證畢。

由定義3和性質2可得B?C，a∈C-B，屬性a相對區分度為：

定義4 給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，對?B?C，?b∈B，定義SIGI(b,B,C)=|DISC(B,U2)-DISC(B-b,U2)|為屬性b相對屬性集B的重要度，稱為相對重要度。

基于以上混合型弱標記決策系統的區分關系和區分度定義，給出相應的屬性約簡算法。

算法1 混合型弱標記決策系統的非增量屬性約簡算法。

輸入：混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉。

輸出：屬性約簡集合B。

步驟1 根據定義，計算屬性集a的區分關系DISC(a,U2)，令pair0=DISC(C,U2)。

步驟2 將|DISC(a,U2)|的值最大的屬性加入約簡集B，令pairj=DISC(B,U2)。

步驟3 計算pairj+1=pair0-pairj，其中j=1,2,…,n，當pairj+1=0，轉到步驟5；否則，轉到步驟4。

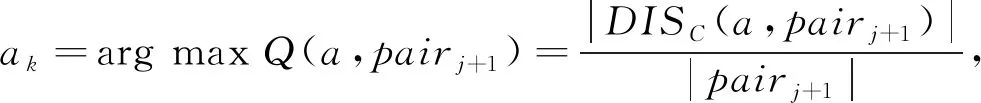
步驟5DISC(B,U2)=DISC(C,U2)，對屬性約簡集合B進行逆向剔除，對任意b∈B，計算屬性b相對B內部重要度，若存在SIGI(b,B,pair0)=0，則B=B-b。

步驟6 輸出屬性約簡集B。

3 混合型弱標記數據的增量約簡算法

數據庫總是呈現動態變化趨勢，非增量算法1在解決屬性動態變化的數據時，需重復計算所有屬性的區分關系，時間復雜度高，甚至無法實現。接下來，給出屬性動態增加時區分關系的增量式更新原理。提出混合型弱標記決策系統屬性增加的增量屬性約簡算法。

3.1 屬性增加時區分關系的增量式學習

定理1 給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，增加屬性p，若有標記的決策子系統的不一致容差類數量發生變化，或無標記的信息子系統的容差類數量發生變化，則新加入的屬性p對于混合型弱標記決策系統的屬性約簡更新是有必要的，否則是不必要的。

證明在文獻[11]中證明了有標記的決策子系統中不一致容差類的數量發生改變，則p是必要的。

無標記子系統中，若?xi,xj∈N,xj∈TC(xi)，當屬性p增加后xj?TC∪p(xi)，則有:

?DISC(C∪p,N2)=DISC(C,N2)∪{(xi,xj)|xj∈TC(xi)∧xj?TC∪p(xi)}，∴DISC(C∪p,N2)≠DISC(C,N2)，?DISC(C,U2)≠DISC(C∪p,U2)，?DISC(redC,U2)≠DISC(C∪p,U2)。

故redC不是〈U,C∪p∪D〉的屬性約簡，即屬性p能區分原來條件屬性C不能區分的樣本對，p是必要的。定理1證畢。

定理2 給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，若新加入屬性p是必要的，則屬性區分關系可用下式更新：

DISC∪p(a,L2)=DISC(a,L2)∪{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠

(6)

DISC∪p(a,N2)=DISC(a,N2)；

(7)

DISC∪p(a,U2)=DISC∪p(a,L2)∪DISC∪p(a,N2)，

(8)

其中：ω(p)={x∈L:|d(TC(x))|>1∧|d(TC∪p(x))|=1}，其中|d(TC(x))|表示x在條件屬性集C下容差類的決策值基數，若|d(TC(x))|的值等于1則表示一致容差類，|d(TC(x))|的值大于1則表示不一致容差類。

證明式(5)的證明，根據區分關系的定義，有標記子系統中加入屬性p后，屬性a的區分關系為

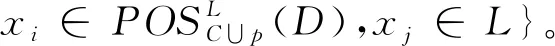
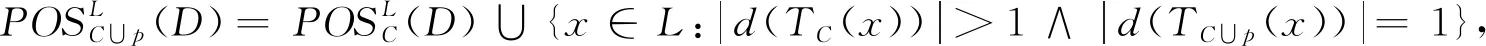
{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠*∧d(xi)≠d(xj),xi∈

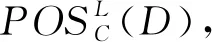
*∧d(xi)≠d(xj),xi∈ω(p)，xj∈|d([x]C∪p)|>1}∪{(xi,xj):f(a,xi)≠

f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠*∧d(xi)≠d(xj),xi,xj∈ω(p)}。

第一部分子集就是屬性a在加入屬性p前的區分關系，再并上原本不一致的樣本在加入屬性p后變成一致樣本的集合與負域中元素的區分對。

DISC(a,L2)∪{(xi,xj):f(a,xi)≠f(a,xj)∧f(a,xi)≠*∧f(a,xj)≠

定理2證畢。同理，可證式(6)成立。

定理3 給定混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，已知其約簡集為redC，當增加必要屬性p，則需更新區分關系DISC(C,U2)，記新增加的樣本對集為Δpairp，若Δpairp?DISC∪p(redC∪p,U2)，則redC∪p就是混合型弱標記決策系統TS′=〈U,C∪p∪D〉的屬性約簡集，否則需要利用屬性相對區分度定義更新屬性約簡集。

3.2 增量屬性約簡算法

基于以上增量學習定理，結合反向刪除法，構造混合型弱標記決策系統中基于屬性相對區分度的啟發式增量屬性約簡算法。

算法2 屬性增加的混合型弱標記決策系統基于區分對的增量屬性約簡算法。

輸入：混合型弱標記決策系統TS=〈U,Cd∪Cr∪D〉，區分關系DISC(a,U2)，令樣本對集pair0=DISC(C,U2)，屬性約簡集redC；新增屬性集合C′。

輸出：混合型弱標記決策系統TS′=〈U,C∪C′∪D〉的屬性約簡集。

步驟1 增加屬性集C′,篩選出必要屬性集C″，若C″=φ，則轉到步驟5；否則轉到步驟2。

步驟2C″≠φ，重復以下步驟：

步驟2.1 若?p∈C″，滿足ω(p)={x∈L:|d(TC(x))|>1∧|d(TC∪p(x))|=1}≠φ，更新DISC∪C′(a,(L∪L″)2)；否則轉到步驟2.2。

步驟2.2 若?p∈C″，滿足φ(p)={x∈N:|TC(x)|>1∧|TC∪p(x)|=1}≠φ，更新DISC∪C′(a,(N∪N″)2)，直到遍歷C″中所有屬性，轉到步驟3。

步驟3 若Δpair0?DISC∪C′(redC∪C″,(U∪U′)2)(其中Δpair0=DISC∪C′(C∪C′,(U∪U′)2)-DISC∪C′(C,U2))，則約簡為redC∪C′=redC∪C″，轉到步驟6；否則轉到步驟4。

步驟4 計算redC∪C′的區分關系，令pairj=DISC∪C′(redC∪C′,U∪U′)；設pairj+1=pair0∪Δpair0-pairj，其中j=0,1,…,n。若pairj+1=0則轉到步驟6；否則轉到步驟5。

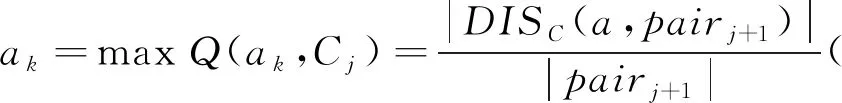
步驟6 對?b∈redC∪C′，計算屬性相對重要度，若存在bk使得SIGIDISC∪C′(bk,redC∪C′，pair2)=0 (其中pair=pair0∪Δpair0)，則屬性約簡為redC∪C′=redC∪C′-bk；轉到步驟7，否則轉到步驟5。

步驟7 輸出屬性約簡redC∪C′。

4 算法實例分析

為進一步驗證本文算法的有效性，在美國加州大學歐文分校提出的數據庫(University of California Irvine，UCI)中選取了6個混合型數據集，如表1所示。實驗的運行環境為：CPU Intel(R)Core(TM)i5-10500(3.20 Hz),內存8.0 GB，操作系統為Windows 10，所運用的軟件平臺為MATLAB2020a。

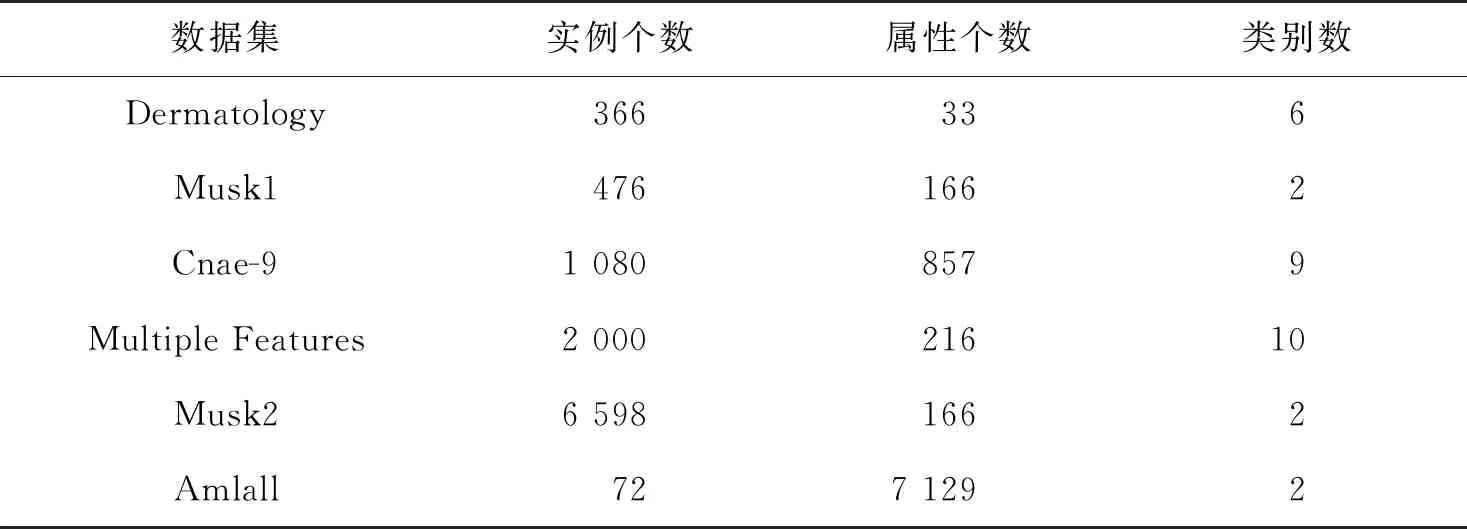
表1 實驗數據集

4.1 數據說明及實驗設計

為模擬現實中數據標記缺失的情形，將6個數據集的標記進行隨機缺失處理，通過文獻[21]可知，隨機標記缺失比例為50%的弱標記數據環境中算法分類性能更好。本部分將討論增量算法2的屬性約簡運行效率和分類性能。以50%條件屬性作為基礎數據，剩余數據作為增量數據集，按照增量數據集大小的10%為梯度遞增時，分別對弱標記的數據采用本文非增量算法1、增量算法2、弱標記數據的半監督屬性約簡算法[19](semi-supervised attribute reduction algorithm for weakly labeled data, Semi-D)和綜合重要性屬性約簡(compute IMP-reduction,CIMR)算法[20]進行屬性約簡，并對4種算法進行簡單的比較分析。

4.2 屬性約簡效率比較

圖1為本文非增量算法1、增量算法2、CIMR算法和Semi-D算法分別在6個數據集中屬性增加時的屬性約簡計算時間比較。由于本文模擬了數據集中按增量數據的10%依次動態增加，因此圖l中每幅圖的橫坐標為屬性與樣本的動態增加比例，刻度值為10%至100%，縱坐標表示每次增加動態數據時屬性約簡所消耗的計算時間。

由圖1可知：隨著混合型弱標記決策系統動態數據集的逐漸增加，本文算法1計算時間增長的速率較快，而增量算法2的增長速率較為緩慢，且CIMR算法和Semi-D算法的屬性約簡計算時間均大幅度高于增量算法2的計算用時。由圖1a～圖1c可知：由于本文算法2引入相對區分度作為屬性重要度的度量標準，在每次迭代中不斷地減少搜索空間，在處理數據規模較小的數據集和本文非增量算法1時，計算效率相近；在小數據集中，如Musk1數據集上本文算法2最終運行時間為187.428 s，而CIMR算法和Semi-D算法運行時間分別為650.365 s和972.315 s，相比CIMR算法節約71.18%，相比Semi-D算法能節約80.72%的時間。隨著數據規模的增大，在圖1d～圖1f中，算法1在動態數據中更新屬性約簡結果需要進行大量的重復計算，采用增量算法2，利用已有的增量機制對屬性約簡集進行增量式更新，能夠減少重復的計算，在Amlall數據集中，當數據集增加100%時，增量算法2的運行時間為1 171.456 s，非增量算法1的運行時間為6 351.258 s，CIMR算法和Semi-D算法的運行時間分別為10 129.458 s和11 078.74 s，相比非增量算法1的計算效率提高了81.5%，相比CIMR算法和Semi-D算法的計算效率分別提高了88.3%和89.42%。

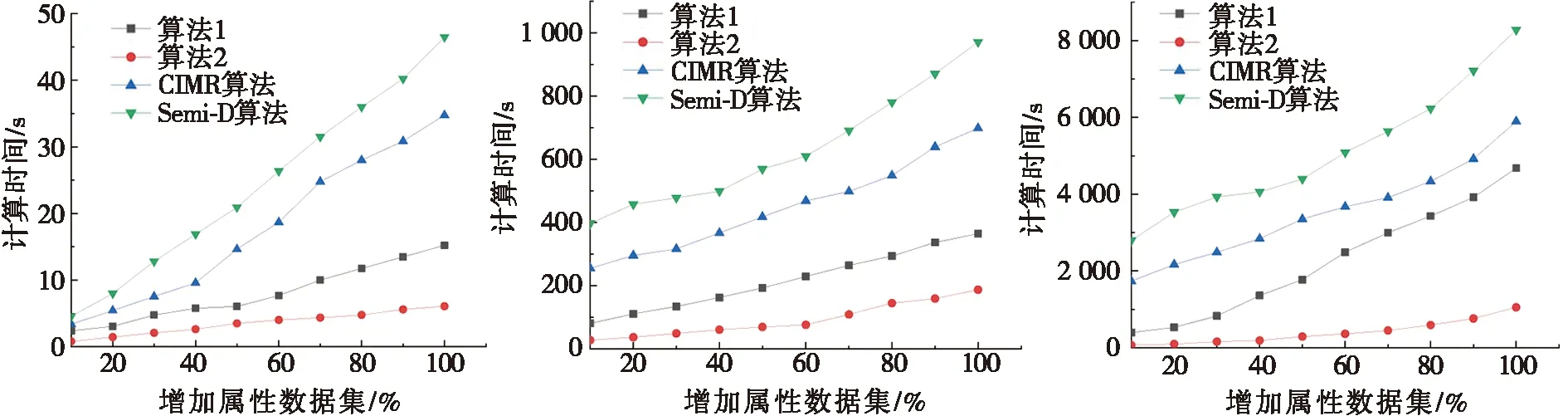
(a) Dermatology (b) Musk1 (c) Cnae-9

4.3 屬性約簡結果及分類性能比較

為了對非增量式與增量式屬性約簡的結果進行比較分析，在實驗的過程中選取了當增加的數據集為100%時的屬性約簡結果輸出來。非增量算法1和增量算法2的屬性約簡結果對比見表2，屬性Ci簡寫為i。表2是數據隨機缺失50%后，弱標記數據集的屬性約簡結果在支持向量機(support vector machines,SVM)和分類決策樹(decision trees,C4.5)兩種分類器下的分類精度。

由表2可知：在不同分類器中同一屬性約簡結果的分類精度有一定差異，但僅利用有標記的數據獲取的屬性約簡結果會丟失部分有效的分類信息，故分類精度顯著偏低，分類器較難準確學習到其內在規則或模式。因此，僅利用有標記的數據獲取屬性約簡結果的分類性能顯著偏弱。而利用本文弱標記屬性約簡算法1和算法2處理6個數據集標記缺失50%的弱標記數據，能夠獲取一個分類性能相對較優的屬性約簡結果。在實驗過程中發現，在不同分類器中屬性約簡結果的分類性能也存在一定差異，本文算法2在規模較小的數據集上對比非增量算法1，由于對小數據集的標記進行隨機缺失，對分類效果產生了一定影響，導致分類性能效果偏弱，但是相比僅用有標記數據處理數據的分類精度高，例如在Dermatology、Musk1和Cnae-9數據集中SVM分類器下，算法1的分類精度均值是80.68，算法2的分類精度均值是80.09，僅用有標記數據約簡結果得到的分類精度均值是61.14。但隨著數據規模的增大，增量算法2的性能表現趨于穩定，例如在Dermatology、Musk1和Cnae-9數據集中SVM分類器下，算法1的分類精度均值是91.18，算法2的分類精度均值是91.11，僅用有標記數據約簡結果得到的分類精度均值是81.23。在 C4.5分類器下，3種算法的分類精度情況類似于SVM分類器，存在0.8以內的偏差。

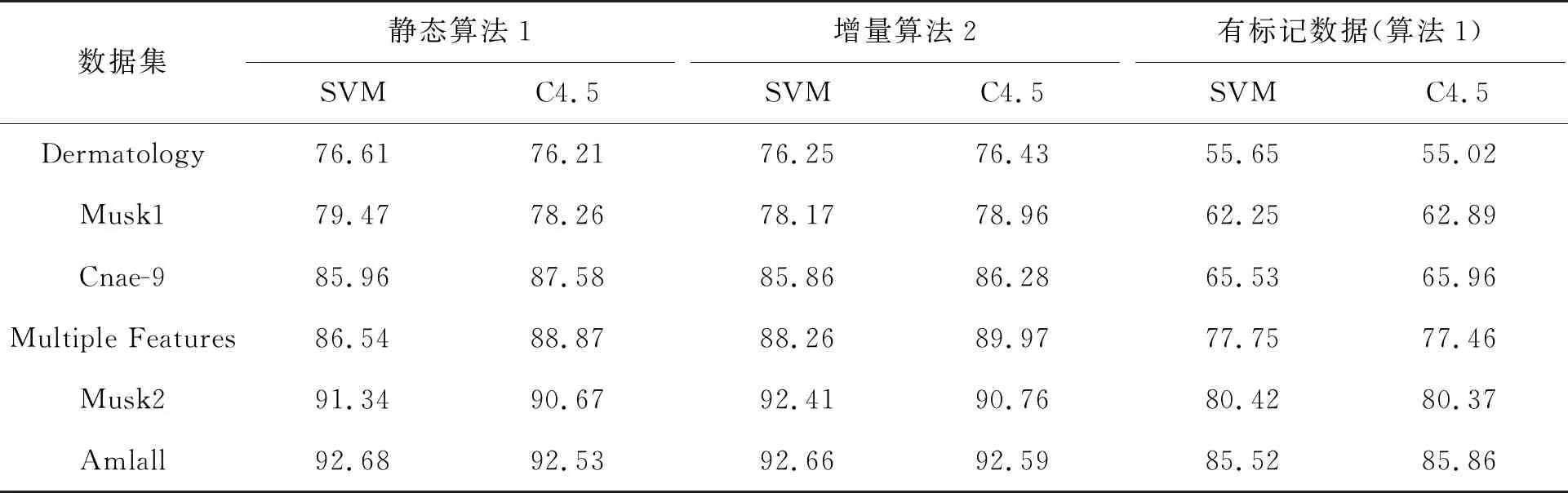
表2 屬性約簡分類精度比較 %

綜上可得，本文提出的增量算法2能夠有效節約大量計算時間，獲取分類性能較優的屬性約簡結果，同時能夠有效利用無標記的數據，增強屬性約簡結果的分類性能，顯著提升了算法的魯棒性。為大規模復雜數據的屬性約簡問題，提供了一個可行的增量式屬性約簡方法。

5 結束語

已有的粗糙集屬性約簡算法往往只能應用于信息系統或單一的決策系統，導致約簡分類性能較低。本文提出的混合型弱標記決策系統中增量屬性約簡算法，能充分利用無標記與有標記數據得到精度較高的約簡結果。給出了明確的增量機制，在處理實際應用中大規模復雜數據集時，相對傳統非增量算法的約簡效率更高。