基于隨機森林算法的港口集裝箱吞吐量預測方法

謝新連，王余寬,2，許小衛，馬 昊

(1. 大連海事大學 交通運輸工程學院,遼寧 大連 116026； 2. 武漢理工大學 航運學院，湖北 武漢 430063)

0 引 言

港口作為海運網絡的重要節點，它的發展與所在區域向海經濟發展互為支撐。港口集裝箱吞吐量是港口管理部門制定港口發展規劃的主要依據之一，如何更加準確地預測集裝箱吞吐量一直是學術界和工程界的研究熱點。

總結已有的研究文獻，港口集裝箱吞吐量預測方法主要包括以下幾種：指數平滑法[1]、多元回歸分析法[2]、灰色預測法[3]、神經網絡預測法[4-7]、組合預測法[8-9]等，各個模型具有以下特點：指數平滑法是對單一變量進行建模分析，難以計算特征變量的影響，對波動幅度大的數據適應性也較差；多元回歸分析考慮特征變量對集裝箱吞吐量的影響，但無法避免特征變量間的共線性效應；灰色模型雖然所需的參數較少，但其快速遞增和衰減的特性導致只適用于短期預測；神經網絡對離散、非線性數據有較好的應用效果，但對訓練樣本容量需求較大，而且容易陷入局部最優；組合預測在計算權重值大小時，精度很難保證。綜上分析，可見已有的方法的局限性限制了港口集裝箱吞吐量預測精度，因此提出對集裝箱吞吐量預測方法的研究是十分必要的。

隨機森林算法(random forest algorithm，RFA)是一種基于決策樹理論的機器學習算法，能夠評估所有特征變量的重要性，同時避免線性分析所面臨的多元共線性的問題，L. BREIMAN[10]描述了隨機森林算法進行多維變量重要性排序以及決策樹構建等技術。隨機森林算法的優勢在于集成了多棵決策樹，可以處理數以千計的特征變量，實驗顯示該算法計算速度較快，準確率較高。目前隨機森林算法在短時交通流預測[11]、熱軋帶鋼質量預測[12]、太陽能輻照度預測[13]等方面已被應用。

筆者將RFA應用于港口集裝箱吞吐量的預測，并將RFA與多元回歸分析、三次指數平滑和BP神經網絡的預測結果比較，結果表明：基于RFA的預測方法預測準確性更高。

1 隨機森林算法

RFA通過組合個體決策樹，并基于投票機制進行決策，包含分類和回歸兩種模型，其中分類模型基于決策樹預測值的多數票進行決策，回歸基于決策結果的平均值進行決策。 在訓練階段，從初始樣本集合中進行bootsrap抽樣(隨機且有放回地抽取), 并對每個bootsrap樣本建一棵決策樹，每棵樹即為一個弱分類器，通過建立多個弱分類器對高維數據間的內在聯系進行分析，然后將多個弱分類器組合, 通過投票機制得出決策結果，進而構成一個強分類器，一個包含K棵決策樹的RFA決策模型結構如圖1。

RFA的特點是：每棵決策樹分割節點的數量是從樣本集特征數量中隨機選擇出來，然后通過定量分析對該節點數量所產生效果進行評估，以決定該棵決策樹的分割節點數量。為所有決策樹隨機提供分割節點數量，這種隨機性使得由眾多決策樹結合起來得到的集合決策樹擁有更好的預測性能。

圖1 RFA決策樹構建示意Fig. 1 Schematic diagram of decision tree construction of random forest algorithm (RFA)

2 集裝箱吞吐量預測模型

2.1 隨機森林結構

RFA預測模型參數包含決策樹數量和節點變量個數。決策樹數量決定預測模型的泛化能力，節點變量個數為單棵決策樹的分裂節點數量，影響決策精確度。一般而言，泛化誤差是在使用bootstrap抽樣法抽樣時，樣本未被抽中導致的，假設樣本數量為N，則樣本被抽中的概率為[1-(1-1/N)N]，當N趨向于無窮時，[1-(1-1/N)N]收斂于0.632，即在總樣本集中存在36.8%的樣本未被抽中，這部分樣本稱為袋外(out-of-bag，OOB)樣本，利用OOB樣本計算模型的泛化誤差稱為OOB估計。OOB估計步驟為：

1)將各個訓練集分別作為OOB樣本，計算RFA決策樹各弱分類器的決策結果。

2)以投票模式選舉得到各個OOB樣本的最終決策結果。

3) 計算每一棵決策樹的OOB估計結果，即每一棵樹樣本分類錯誤數量與樣本總數的比率。模型的泛化誤差計算式為：

(1)

式中：EK為包含K棵決策樹的RFA模型的泛化誤差；ε[yn,Ck(xn)]為對第n個訓練樣本的OOB估計誤差進行計算；xn為第n個訓練樣本；yn為第n個訓練樣本的分類結果；Ck(xn)為K棵決策樹對xn的決策結果。

對于組成RFA模型的每棵決策樹，均可計算得到一個OOB估計誤差，進而通過式(1)計算得到模型的泛化誤差EK。計算不同決策樹數量時模型的泛化誤差，當泛化誤差最小時即獲得最優決策樹數量。而節點變量個數的最優值一般為特征變量數量的1/3，實例數據中特征變量為17個，則需要分別計算并比較節點變量個數為5和6時的模型決策誤差，選取決策誤差較小時對應的值為RFA模型的節點變量個數。

2.2 變量重要性分析

為了提高RFA的預測精度，需要確定影響港口集裝箱吞吐量相關變量，并計算其影響程度。(mean decrease in accuracy, MDA)是用來衡量變量重要性的參量，MDA基于OOB估計來計算，其值直接表示該變量對模型預測準確度的降低程度，值越大表示該變量對港口集裝箱吞吐量的影響越大。用Mv表示第v個變量的MDA值，其計算公式為：

(2)

式中：t為RFA模型的決策樹數量；en為第n個樣本的OOB估計誤差。

對所有變量進行多次重要性分析，求其分值平均值并排序，從樣本集所有特征變量中排除冗余特征變量，并對分值計算結果結合實際分析，篩選出V個對集裝箱吞吐量影響程度較大的特征變量，組成預測模型的變量集合。

2.3 決策模型

基于篩選出的具有重要影響的特征變量樣本集，運用bootstrap方法隨機抽得b個樣本，然后從所有特征變量中隨機選取v′個變量，即得到一個樣本集。重復以上操作A次，則得到由A個獨立樣本集形成的總樣本集。對各樣本集構建決策樹模型，得到包含K棵決策樹的隨機森林。最后通過每棵樹投票形式尋找得分最高結果作為預測的結果。最終獲得的RFA模型為：

(3)

2.4 評價指標選取

為驗證隨機森林算法對集裝箱吞吐量的預測效果，采用相對誤差Er(relative error)、平均絕對百分比誤差EMAP(mean absolute percentage error)、均方誤差EMS(mean square error)、和均方根誤差ERMS(root mean square error)4個指標來檢驗模型的預測精度。ER用來評價預測方法中每一個測試樣本的預測效果，EMAP、EMS及ERMS作為模型整體預測效果的誤差檢驗方法，4個指標計算如式(4)～式(7)：

(4)

(5)

(6)

(7)

式中：ER,n為第n個樣本的相對誤差；xn,r和xn,p分別為第n個測試樣本的真實值和模型預測值；N為測試樣本數量。

3 應用實例

3.1 變量獲取

從中國交通運輸統計網、《大連市統計年鑒》、《遼寧統計年鑒》和《中國統計年鑒》中獲取所需數據，時間域為2000年—2019年，其中2000年—2014年數據作為預測模型的訓練樣本集，2015年—2019年的數據為驗證樣本。

影響集裝箱吞吐量預測的環境因素較多，表1統計了港口集裝箱吞吐量數據和可能對集裝箱吞吐量產生影響的17個特征變量，包括區域生產總值、周邊港口集裝箱吞吐量、東三省對外貿易量等，實驗選取18個變量的所有數據構成預測模型的總樣本集。

表1 模型變量Table 1 The model variables

3.2 模型參數優選

一般而言，節點變量個數為特征變量個數的1/3，本例中通過實驗得到節點變量個數為6時，RFA預測誤差最小。圖2給出了不同的決策樹數量所導致的模型誤差，當決策樹數量為500時模型誤差達到最低點，因此，選擇決策樹數量為500。

圖2 模型決策樹誤差Fig. 2 Model decision tree error

3.3 變量重要性分析及特征優選

根據MDA分析原理得變量重要性分值，如表2，第三產業增加值、營口港集裝箱吞吐量、大連市生產總值的重要性較大，分值在7以上；遼寧省生產總值、遼寧省對外經貿總額等6個變量重要性分值在5～7之間；而機場旅客吞吐量的重要性分值則不足3，說明該變量對模型的增益效果很低。

根據變量重要性排序，依次疊加選取重要性最高得變量，將所選變量組成特征集合進行集裝箱吞吐量預測。隨著特征變量個數得增加，模型預測準確度變化趨勢如圖3。變量數目小于5時，預測準確度隨變量數目增加而顯著提升；在變量數量為9時，預測準確度為95.66%，達到峰值；在變量數目為16時，即把機場旅客吞吐量加入特征變量集合時，預測準確度出現較大波動。由此看出，預測準確度并非嚴格隨變量數目的增加而升高，這說明部分變量對港口集裝箱吞吐量預測有干擾，此類冗余特征的刪除有助于提升預測準確度。因此，研究提取重要性排序前九的變量數據進行預測建模，篩選出的變量既可用于隨機森林模型預測，亦可在其他預測方法中應用。

表2 變量重要性得分Table 2 Importance score of variables

圖3 預測準確度與優選變量數目關系Fig. 3 Relationship between prediction accuracy and the number of preferred variables

3.4 預測結果分析

將RFA預測結果與多元回歸分析法、三次指數平滑法以及BP神經網絡預測法的預測結果對比分析。4種方法對2015年—2019年大連港集裝箱吞吐量的預測值及誤差如圖4，顯而易見：相比于其它3種方法，RFA預測結果更接近實際值，并且在不同年份的預測波動較小。

圖4 4種模型預測值Fig. 4 Forecasting results of four kinds of models

如表3為4種模型的預測值及誤差，其中平均誤差值為各年預測誤差絕對值的平均值。RFA預測值平均誤差率為4.34%，各年絕對誤差最大值為5.65%，而多元回歸和BP神經網絡的平均誤差率均接近10%，三次指數平滑平均誤差率大于10%，絕對誤差率高達22.8%，可見RFA預測最接近實際值。

圖5展示了4種模型預測結果總體相對誤差分布，可以看出，多元回歸相對誤差為負值，三次指數平滑和BP神經網絡均為正值，說明此3個模型預測結果均出現偏離實際值現象，而隨機森林相對誤差在0附近說明其預測結果貼合實際值。據圖4和圖5可知，隨機森林模型在各個年份可提供較為準確的單點預測效果。

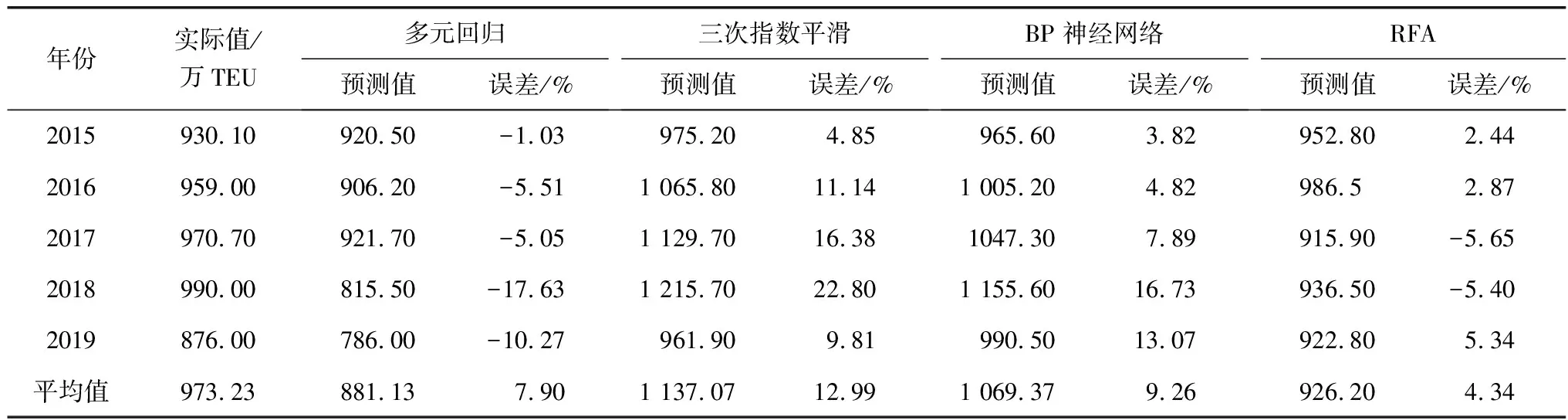
表3 模型預測值及誤差Table 3 Model prediction values and errors

圖5 4種模型預測箱線圖Fig. 5 Boxplot diagram of four kinds of models

為了進一步驗證RFA的預測性能，對4種模型的EMAP、EMS和ERMS指標進行分析，如表4。可見，RFA的EMAP低于5%，其EMS僅為其它模型的20%左右，ERMS值也在各個模型中最低。在各個指標表現上，多元回歸和BP神經網絡表現較為相似，而三次指數平滑EMAP達到12.99%，在各個指標中表現均為最差。可知，隨機森林預測各項誤差評價指標上均優于其他3個預測方法，預測性能優勢顯著。

表4 模型評價指標Table 4 Model evaluation index

通過實驗分析，RFA在進行具有時間特性的港口貨物吞吐量預測中，預測結果更接近實際值，預測誤差也明顯低于BP神經網絡模型、多元回歸分析法和三次指數平滑法。同時，RFA在保證準確預測吞吐量整體變化趨勢的基礎上，在較長時間內對各個年份的單點預測結果也較為接近實際，提高了吞吐量預測的準確性。

4 結 語

港口集裝箱吞吐量的預測與復雜的環境影響變量相關，隨機森林算法消除了特征變量的共線性影響，并基于MDA分析各變量的影響程度，篩選出有重要影響的特征變量，其中第三產業增加值重要性分值最高，營口港集裝箱吞吐量重要性排名第二。第三產業的發展是經濟發展的關鍵體現，而營口港作為大連港的近鄰港口，則會因同質競爭而出現吞吐量間的重要關聯性，可以預見，重要變量分析結果將有助于分析港口發展與經濟發展的關聯性，輔助港口管理人員對港口間協同發展進行合理規劃。

根據變量優選結果對2015年—2019年大連港集裝箱吞吐量進行預測，與三次指數平滑法、多元回歸分析和BP神經網絡的預測結果相比誤差更小，預測性能更優。一定程度上預測結果將有助于港口管理人員更好地規劃港口貨源供應、貨場分布、泊位布局以及水陸交通樞紐建設等。根據大連自貿港建設規劃研究，目前遼寧省內港口間存在貨源分布差異大的現象，這導致部分港口出現貨源過量而無處安放問題，通過吞吐量預測可分析得到港口貨物需求量，進而根據需求提供貨物量，這將有助于港口規劃貨源供應以及貨場分配等，更好地節約和利用社會資源。

隨著海洋強國戰略的部署和實施，航運業向著智慧航運的方向發展。應用隨機森林算法預測港口集裝箱吞吐量，更加準確、高效、合理地助力港口建設，助力政府推進智慧航運發展。