高速公路合流區可變限速和換道協同控制研究

李巧茹，王少航，陳 亮

(河北工業大學 土木與交通學院，天津 300401)

0 引 言

交通需求增加導致高速公路合流區通行能力下降，擁堵問題頻發。通過智能交通技術來提高現有公路基礎設施效率，成為智能交通控制領域研究的熱點。

可變限速(VSL)控制是最常用的控制策略之一。VSL通過調整交通瓶頸上游的速度限制，可以提高交通流的機動性[1]、安全性，并減少污染和降低能耗。J.R.D.FERJO等[2]基于模型預測控制(MPC)設計了可變限速控制策略；G.R.IORDANIDOU等[3]將局部反饋MTFC應用于交通瓶頸可變限速研究；C.RONCOLI等[4]研究發現，接近瓶頸處車輛的強制換道行為可能導致這些VSL方法效果不理想；Y.ZHANG等[5]指出，現有的大多數VSL方法在微觀仿真中對交通流動性的改進不大，并首次提出結合VSL和換道(LC)控制的協同控制方法。

在某些情況下，VSL控制產生的限速值可能很小，甚至小于20 km/h，與高速公路實際限速要求相悖。C.B.ZHANG等[6]通過優化車輛在車道上的分布，減輕了車道變化路段強制換道的負面影響；田麗萍等[7]針對高速公路合流區，提出一種主線段車輛動態限速方法，通過主線車輛減速來避免車輛合流時的沖突；E.YE等[8]提出了一種二級交通控制方法，優化合流區上游車道的車輛密度，并建議沖突車輛提前變道。然而，當交通需求較高時，僅采用LC控制不足以減少交通擁堵。Y.ZHANG等[9]結合VSL和LC控制，為交通事故點上游的車輛提供換道建議；Y.GUO等[10]提出了一種智能網聯車輛(CAVs)環境下集成的VSL和LC的控制方法，考慮VSL和LC相互作用，以最大限度提高交通效率；陳亮等[11]設計了一種基于多分類支持向量機的車輛換道識別模型，為微觀交通仿真提供了技術支持；T.L.PAN等[12]提出了一種新的中觀多車道CTM模型，能夠同時模擬強制和任意改變車道的行為，并可用于預測交通事件發生或車道控制策略的仿真。

綜上，將VSL和LC相結合的協調控制研究較少，尤其是在LC控制中未考慮由LC控制本身對交通流的干擾。筆者將換道控制造成的容量下降引入LC控制中，減少車輛自主變道對主線交通流的干擾，并與VSL結合，以期提高控制系統對不同交通需求的適應性。

1 公路瓶頸模型

交通瓶頸是指通行能力最低的點，由于交通瓶頸的存在，隨著交通需求的增加，會出現車輛排隊現象。車道數變少、交通事故發生、合流區的車輛匯入或其他道路狀況都可能導致交通瓶頸，交通瓶頸的流量決定了整個公路路段的通行能力。因此，瓶頸處交通流的建模對于設計有效的交通控制策略至關重要。

圖1為高速公路合流區瓶頸示意，由一條3車道的高速公路主線路段和單車道的入口匝道組成。設高速公路主線的通行能力為C，匝道車輛能全部順利匯入高速公路主線段。當匝道上的交通需求為0時，瓶頸處的理想通行能力Cb=C；當匝道上的交通需求為qr=ρrvr時，從匝道匯入主線的車輛將在加速車道路段對主線車流形成交通障礙，此時瓶頸處的理想通行能力Cb=C-qr。根據三角形基本圖假設，瓶頸上游密度ρd較低時，瓶頸上游理想流量qb=vfρd，其中vf為高速公路主線自由流速度；而當瓶頸上游密度ρd大于臨界密度ρdc，即瓶頸的需求大于其容量Cb時，停滯的車輛將在瓶頸上形成車隊，并向上游傳播。車隊中的車輛強行改變車道會降低其他車道上車流速度，降低瓶頸容量[13]。瓶頸路段流量-密度關系如圖2，圖中q為流量，ρ為密度。當隊列形成時，容量將下降到C′b=(1-ε)Cb，且ε∈(0,1)，ρd與qb的關系如下：

(1)

Cb=vfρd

(2)

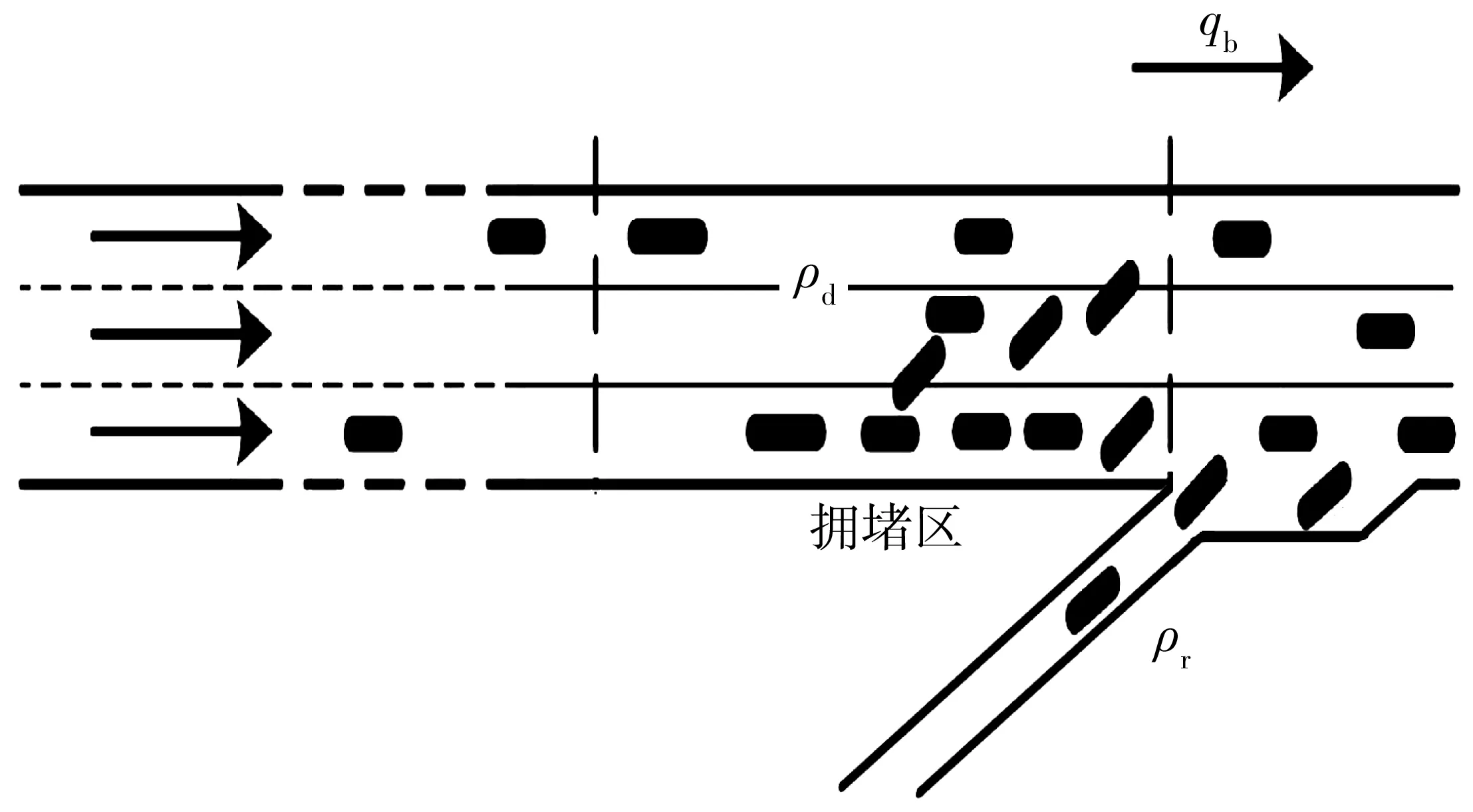
圖1 高速公路合流區瓶頸示意Fig. 1 Schematic diagram of bottleneck in expressway confluence area

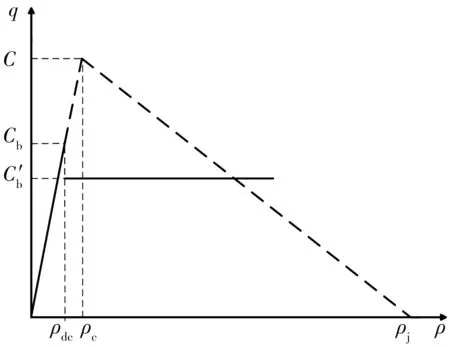
圖2 瓶頸路段流量-密度關系Fig. 2 Flow-density relationship of bottleneck section

2 基于元胞傳輸模型的可變限速研究

2.1 元胞傳輸模型

元胞傳輸模型將高速公路主線段分成N段，分別用qi、ρi、vi、Li來表示元胞i={1,2,…,N}的流量、密度、平均車速和路段長度，并在每個時間間隔t對各個元胞的交通狀態參數更新。經典的CTM模型(圖3)中Qc為路段通行能力，vf為自由流速度，ρc為關鍵密度，w為交通波傳播速度，ρj為堵塞密度，vvsl為可變限速值，Q′c、ρ′c分別為可變限速下的路段通行能力和關鍵密度。

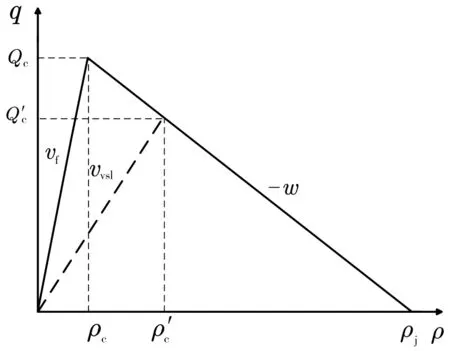
圖3 可變限速路段流量-密度關系(CTM模型)Fig. 3 Flow density relationship of variable speed limit section (CTM modle)

t時刻元胞的流量和速度如式(3)、式(4)：

qi(t)=min{vi-1(t)ρi-1(t),Qc,[ρj-ρi(t)]w}

(3)

(4)

由此可得元胞t+1時刻密度為：

ρi(t+1)=ρi(t)+[qi-1(t)-qi(t)]/Li

(5)

2.2 限速下的元胞傳輸模型改進

可變限速下元胞傳輸模型如圖3中斜率為vvsl的虛線，此時車輛的最大速度由自由流速度vf變為限速值vvsl，可變限速下的通行能力Q′c和對應的關鍵密度ρ′c為：

Q′c=vvslwρj/(vvsl+w)

(6)

ρ′c=Q′c/vvsl

(7)

當元胞密度小于等于關鍵密度時，車輛不再以自由流速度行駛，而是以限速值vvsl行駛；當元胞密度大于關鍵密度時，車輛期望速度小于限速值，車輛將以期望速度行駛，即：

(8)

元胞i的流量為：

qi(t)=min{ρi-1(t)vi-1(t),Q′c,[ρj-ρi(t)]w}

(9)

元胞密度是由上一時刻的元胞密度和元胞流量決定的，不受限速值的影響，故元胞密度表達式與式(5)一致。

3 可變限速與換道協同控制

3.1 換道協同控制

換道協同控制應用于合流區上游，如圖4。換道控制的目的是降低高速公路右側車道的車流密度，通過控制使主線車輛提前變道，以便入口匝道車輛能夠順利匯入高速公路主線。在保證交通順暢的情況下，通過使合流區上游的車輛變道，減少靠近合流位置的車輛數，最大限度減少車輛匯入干擾，降低交通流的惡化程度，減少容量下降的影響。圖中，vi,vsl、qi、ρi、Li分別為元胞i={1,…,N}的限速值、流量、密度以及路段長度，qb為從主線匯入合流區的流量，ρr為匝道車流密度。

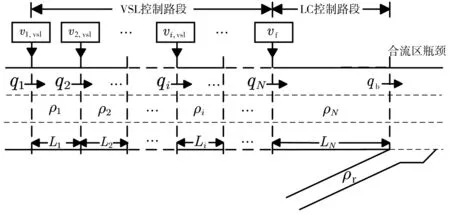
圖4 協同控制示意Fig. 4 Schematic diagram of collaborative control

換道控制通過最小化目標函數確定每條車道上的最優車輛數，并在每個時間間隔向智能網聯車輛(CAVs)提供換道建議，以實現最優車流密度分布。換道控制的目標為采用較小的變更車道次數實現每條車道的最佳車輛密度。由于控制是通過給車輛提供變道建議來實現，采用控制路段的車輛數來代替交通密度，代替后的最優車流密度的目標函數如式(10)：

(10)

(11)

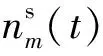
理想車道車輛數的表達式如式(12)：

(12)

式中：γ為匝道干擾系數，γ越小換道區最右車道的車輛數越小，匝道車流匯入就越順利；ρc是由CTM基本圖得出的臨界密度；ρrp為匝道的預測密度；L為換道控制路段長度，即LN=L。

換道控制模型中假定車輛在換道區只向左進行換道，且換道前、后的車輛數守恒，據此作出如下約束條件：

(13)

(14)

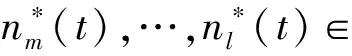
(15)

式中：W為換道區隨機車道編號，W∈[1,l]。

式(13)～式(15)分別保證了車輛數守恒、向左換道規則以及控制車輛數為整數的原則。

車輛換道會對上游交通產生干擾，造成交通擁堵和道路容量下降[14-15]。為了達到最佳的車流密度，需要大量車輛在換道區進行換道，但過多的換道行為或過度控制都會導致系統惡化，造成交通震蕩，影響交通安全。在保證換道不會導致上游交通流惡化的前提下，要維持一定流量，存在一個車道變化的最大數量，其對應的單位長度最大換道率與主線段的平均車道流量的關系如下：

(16)

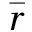
(17)

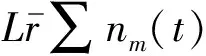
3.2 換道控制的影響

為了研究3.1節提出的合流區變道控制效果，采用MATLAB建立CTM模型，構建一個長為8.4 km的3車道高速公路路段，如圖1。設匝道需求為1 500 veh/h，在未使用VSL的前提下，利用中觀CTM模型研究不同交通需求水平下，瓶頸上游流量qb與瓶頸上游換道區密度ρd間的關系。

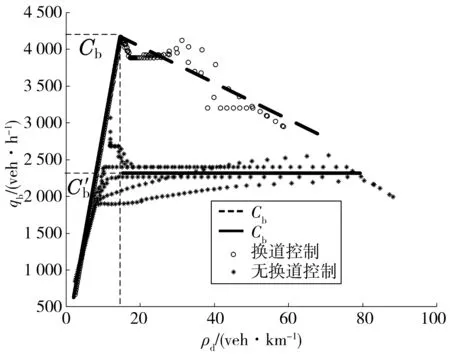
圖5 LC控制路段流量-密度關系Fig. 5 Flow density relationship of LC control section

由圖5可知：采用LC控制時，瓶頸的容量Cb≈4 160 veh/h，對應的關鍵密度ρdc=14.75；當無LC控制時，qb在達到關鍵密度ρdc前就達到了最高值(約為2 400 veh/h)。在無換道控制下，瓶頸上游車輛由于在接近瓶頸前未能提前換道，故在瓶頸處被迫強制換道并造成瓶頸附近車輛大幅減速，最終導致主線容量下降。說明LC控制能夠減少瓶頸處排隊長度，并降低車流密度，使系統具有連續性。

由LC控制下流量-密度關系可知，當上游交通需求小于等于瓶頸容量時，換道區以及合流區車輛以自由流速度vf通過瓶頸；反之，換道區以及合流區由于密度過大造成車輛平均速度降低，最終導致瓶頸截面流量下降，換道控制下的瓶頸流量和密度關系如式(18)：

(18)

式中：qb為換道區流入合流區的流量；wd為換道區瓶頸交通波傳播速度；ρdj為換道區瓶頸堵塞密度。

3.3 可變限速值的確定

雖然換道控制能夠避免高速公路主線容量下降，恢復CTM模型的連續性，但當需求大于瓶頸容量Cb時，合流區仍會出現擁堵。所以還需要在換道區上游設計一個VSL控制器來穩定上游交通流。均勻化所有截面密度，使它們收斂到一個對應瓶頸最大流量的臨界密度ρe。

當上游交通需求小于等于瓶頸容量時，限速值為自由流速度vf。反之，為了控制進入可變限速路段的車流量，需要降低可變限速路段的限速值，依據可變限速控制的期望密度ρe和圖5中的流量-密度關系，可變限速控制路段1的期望限速值和期望密度應滿足：

(19)

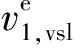
可變限速控制路段1的期望限速值和期望密度可由公式(19)得出：

(20)

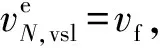
3.4 基于模型預測控制(MPC)的可變限速控制

傳統的PID控制模型因其結構簡單、易于實現而被廣泛應用，但是由于模型采用當前狀態進行反饋，所以對交通流的控制存在一定的滯后。MPC通過當前交通流參數預測未來交通狀態，避免了控制滯后，達到短時間間隔最優控制效果，筆者在MPC的框架下提出可變限速控制系統如圖6。

基于MPC的可變限速系統，以改進的CTM模型作為預測模型，并通過檢驗換道區的實測交通密度ρd與期望密度ρdc的偏差，對基于模型的預測限速值進行反饋修正。可變限速的修正值如式(21)：

u1(k)=KI[ρd(k-1)-ρdc(k-1)]

(21)

式中：u1(k)為第k限速周期內的對可變限速路段1的限速修正值；KI為限速修正值的反饋系數。

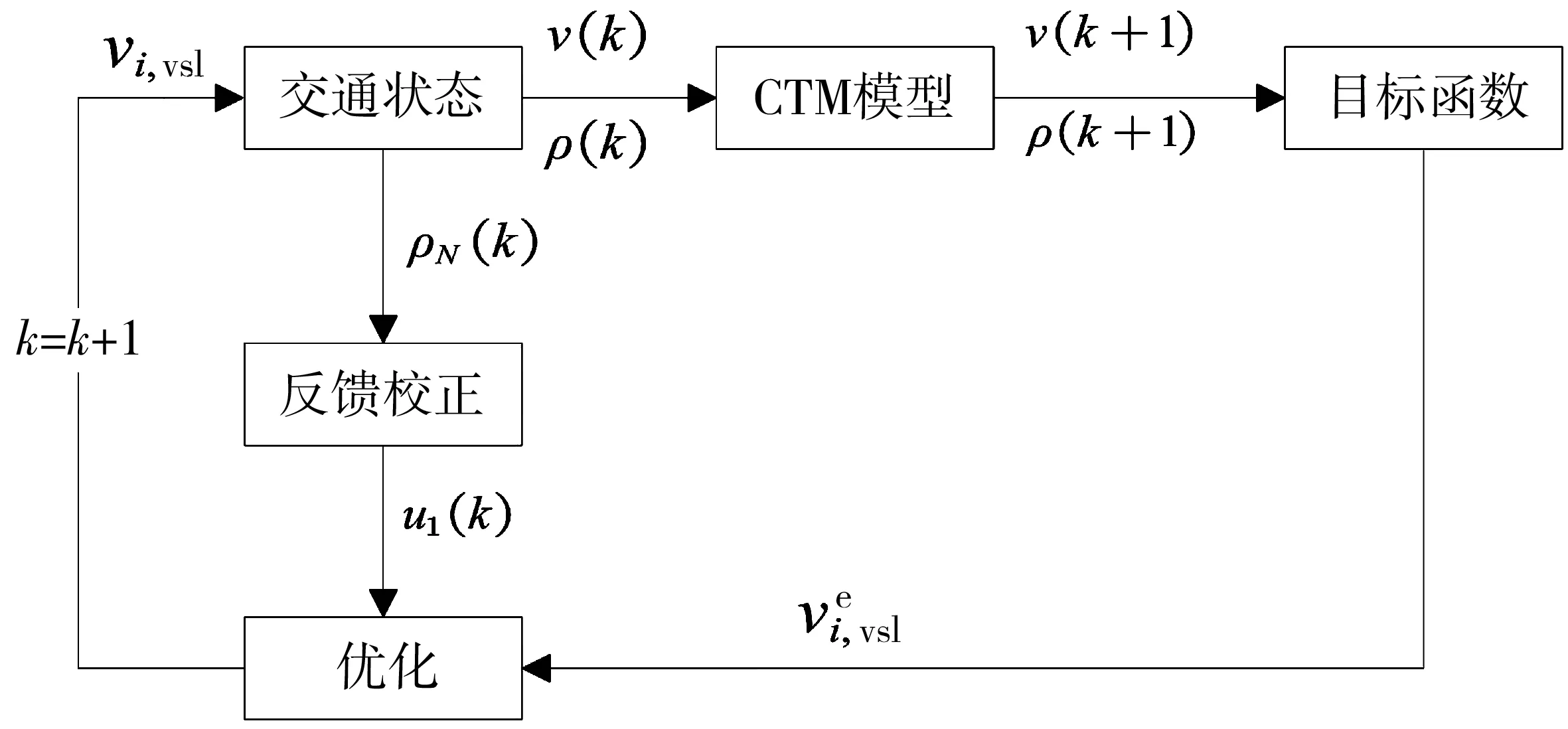
圖6 基于MPC的可變限速控制模型Fig. 6 Variable speed limit control based on MPC

3.5 可變限速控制的約束

由于車輛難以適應過大的限速變化幅度，而且為了交通安全和道路使用者的體驗，速度限制不能過高或過低，故對可變限速值采用以下限制：

1)控制周期。可變限速控制應采用離散的控制周期Tk，且控制周期Tk應為數據采集周期Tc的整倍數。

2)可變限速值的選取。考慮駕駛員的可操控性，可變限速值一般選取5 km/h的整倍數，且最大限速值不得超過自由流速度vf，最小值不得小于靜態限速的最小值，一般取40 km/h。

3)限速變化幅度。為安全考慮，可變限速值在空間和時間上的變化幅度都不宜過大，限速變化幅度一般取5 km/h的整倍數，分別選取10、20 km/h作為可變限速在不同時間同一路段以及同一時間不同路段的最大變化幅度。

4 仿真與分析

4.1 仿真場景與參數設置

為測試和評估協同控制系統性能，利用宏觀和中觀CTM模型在MATLAB中分別對無控制、VSL控制以及筆者提出的協同控制進行仿真。使用宏觀模型來評估筆者提出的協同控制中VSL控制器的性能，由于宏觀模型未考慮車道變換的影響，因此將LC控制模型應用到相應的中觀模型中，利用中觀模型數據對宏觀元胞傳輸模型進行對接校正，并假定車輛對協同控制的服從率為100%。

仿真場景如圖7，合流區上游是一條3車道的路段，主線段中每個路段的長度為600 m，靜態限速為95 km/h，容量為5 700 veh/h；匝道長度與加速車道長度均為200 m，靜態限速為60 km/h，容量為1 500 veh/h。

圖7 仿真路段與場景設置Fig. 7 Simulation section and scenarios setting

仿真中的單車道交通需求曲線如圖8，入口匝道上的峰值流量為1 000 veh/h，主車道上的峰值流量為5 000 veh/h，仿真時間為120 min，峰值時間為20 min。限速路段的設置長度若過長，則無法實現對瓶頸區域交通的有效限制；若距離過短，則一旦瓶頸區域排隊上溯將導致限速控制失效。因此，參考文獻[11]取限速路段長度為500～600 m。

圖8 交通需求設置Fig. 8 Traffic demand setting

限速標志設置在路段9、10、11的起始點，交通流在限速段被限流，并將流量控制在瓶頸容量附近。路段12為速度釋放段，作用是使車輛從限速狀態下的高密度，恢復到自由流狀態下的低密度。路段13為換道控制段，通過給CAVs車輛提供變道建議，調整主線段車流密度，為入口匝道的車流匯入提供良好的環境。

模型及仿真參數設置如表1，表中α1、α2、α3、β為換道控制目標函數的加權系數，α1、α2、α3的數值依次變小，代表越靠近右側的車道受到匝道車輛匯入的影響越大；β的設置考慮了瓶頸流量與換道總次數的綜合影響；Kc為可變限速控制周期內限速值向期望密度調整的速率。

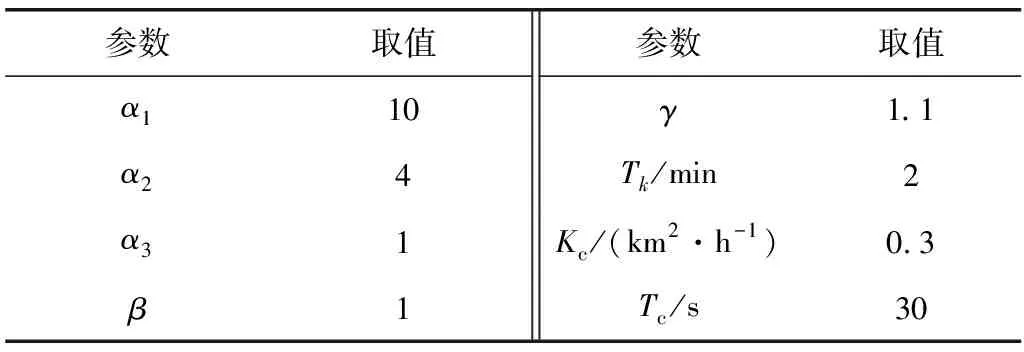
表1 模型及仿真參數Table 1 Model and simulation parameters

4.2 仿真結果分析

由瓶頸理論可知，當換道區密度為期望密度ρdc時，合流區流量達到最大值，此時合流區密度接近關鍵密度20 veh/km。可變限速的目的就是在交通需求過大時限制瓶頸上游的容量，將換道區密度維持在期望密度附近，達到合流區流量最大化，瓶頸容量與換道區流量差為容量下降值，容量下降值越小道路利用率越高。

圖9～圖11分別為無控制、VSL控制、協同控制下交通狀態變化情況。

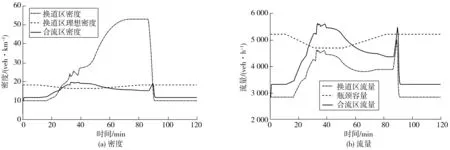
圖9 無控制下交通狀態Fig. 9 Traffic state without control

圖10 VSL控制下交通狀態Fig. 10 Traffic state under variable speed limit control

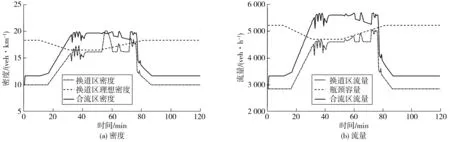
圖11 協同控制下交通狀態Fig. 11 Traffic state under cooperative control

由圖9可知：無控制下的換道區密度隨著交通需求的增加而迅速增加，其峰值遠遠超過了換道區的理想密度，并且在50 min交通需求下降后換道區密度仍保持峰值不變，直到80 min換道區密度才迅速下降；換道區流量在交通需求高峰時段明顯低于瓶頸容量，其差值即為合流區瓶頸的容量下降值。

由圖10可知：換道區密度隨著交通需求的增加而迅速增加，其峰值高于換道區的理想密度且明顯低于無控制下的換道區密度峰值，在50 min交通需求下降后換道區密度隨著時間呈階梯式下降；VSL控制下換道區流量在交通需求高峰時段也明顯高于無控制下的換道區流量，合流區瓶頸的容量下降減少。

由圖11可知：換道區密度隨著交通需求的增加而增加，在交通需求高峰時段，換道區密度穩定在換道區的理想密度附近，換道區流量也穩定在合流區瓶頸容量的附近。與其他控制方案相比，協同控制下的換道區密度與合流區瓶頸容量下降數值明顯變小。從換道區和合流區交通狀態變化情況可以看出，協同控制下的交通流在交通需求高峰時段后能更快地恢復到自由流狀態。

圖12為3種控制方案下換道區密度和合流區流量變化情況。由圖12可知：協同控制下的換道區密度一直低于其他兩種控制方案，且20～80 min時段內，VSL控制和無控制下的換道區密度均出現驟增和驟降現象，而協同控制下的換道區密度變化較為平緩，無控制、VSL控制以及協同控制下的換道區密度的波動范圍分別為11～53、11～32、11～20 veh/km。協同控制下的合流區流量一直高于其他兩種控制方案，且在交通高峰時段內，瓶頸區域通行交通量維持較高狀態，無控制、VSL控制以及協同控制下的合流區流量分別維持在4 423～5 464、4 791～5 611、5 292～5 685 veh/h。由此可知，相較其他兩種控制方案，協同控制能有效提升瓶頸區域的安全性能和通行效率。

圖12 3種方案下控制效果對比Fig. 12 Comparison of control effects of three kinds of schemes

為進一步說明協同控制的性能，采用瓶頸處的平均流量和平均旅行時間兩個指標來說明。仿真發現，主線交通需求增長在17 min時開始影響合流區，為了數據精確，在仿真中選取測量時間為17～80 min，測量路段為路段13～路段14。

設測量時間通過瓶頸的車輛數為N(t)，每車道密度為ρm，則平均旅行時間Tavg和平均流量Qavg的定義為：

(22)

不同策略下的平均旅行時間Tavg和平均流量Qt如表2。

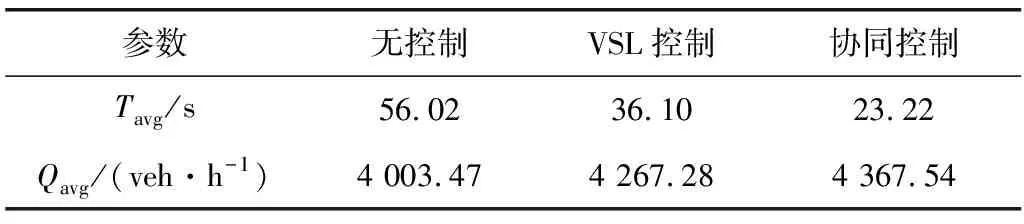
表2 協同控制評價指標Table 2 Evaluation index of collaborative control

由表2可知：協同控制在旅行時間和平均流量這兩個評價指標上都明顯優于其他方案。與無控制方案和VSL控制方案相比，協同控制的平均旅行時間分別降低了58.55%、35.68%；平均流量分別提高了9.09%、2.35%。綜上，提出的協同控制在通行效率、交通安全方面均有明顯改善。

5 結 語

基于CTM模型設計了高速公路合流區可變限速和換道協同控制策略，在提出的協同控制策略中，LC控制通過預測瓶頸容量和交通需求為聯網車輛CAVs提供變道建議，緩解瓶頸處通行能力下降的現象，并利用基于MPC框架的VSL調控瓶頸上游流量，使上游車流密度收斂到期望密度下的平衡狀態，從而實現瓶頸處的流量最大化。為驗證所提出的協同控制策略的性能，利用改進的CTM模型在MATLAB軟件中進行仿真，并采用對比分析的方法對協同控制策略的性能進行分析和評價。仿真結果表明:提出的協同控制策略能有效緩解合流區瓶頸在車流高峰期的容量下降現象，提高合流區瓶頸的通行能力；與無控制方案和VSL控制方案相比，協同控制的平均旅行時間分別降低了58.55%、35.68%；平均流量分別提高了9.09%、2.35%。