融合CZT頻譜細化算法的InSAR相位濾波方法

張繼超，李繼虎，趙鵬飛，林泓全

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.遼寧工程技術大學 軟件學院，遼寧 葫蘆島 125105)

0 引言

合成孔徑雷達干涉測量技術廣泛應用于大區域的地表高程反演和長期形變監測，其原理是通過對同一地表區域多次觀測的SAR影像進行干涉，從而獲取較高精度的干涉相位信息，干涉相位圖的質量直接決定干涉相位測量的精度。在InSAR干涉測量中，由于地表環境復雜、大氣環境因素導致的傳感器接收地表信號不佳和受到熱噪聲去相干、時間去相干、基線去相干以及信號去相干等多種因素影響而產生噪聲復雜區域，在濾波效果較差的情況下會導致解纏過程中由于產生較多奇異點使得相位解纏精度下降，甚至無法解纏，而且還會導致后續衍生產品質量不佳[1-2]。因此，為了減小噪聲對干涉測量結果產生的負面影響，并保證干涉測量結果的準確，在相位解纏之前對干涉相位進行適合的濾波是必不可少的。

現階段，用于干涉相位濾波的方法大致分為頻率域濾波和空間域濾波。空間域濾波主要有均值濾波、中值濾波和圓周期均值等方法，其原理簡單、運算速度快，但沒有考慮干涉相位圖的實際含義，濾波效果不盡人意，而且在濾波窗口的選擇上有一定難度，在干涉條紋密集區域容易破壞細節，出現失真的情況。隨著空間域濾波的發展，又有學者將自適應濾波和自適應窗口大小的濾波方法等相關技術應用于干涉相位濾波中，例如精細Lee濾波，通過自適應的方法可以根據圖像的紋理特征相似性來更好地消除噪聲并保留圖像中的細節，但其計算復雜，而且仍舊無法很好保留干涉跳變信息[3-4]。頻率域濾波是將圖像變換到頻率域，通過去除高頻噪聲部分從而實現濾波[5]。1998年，Goldstein和Werner提出了一種在頻率域中的自適應干涉相位濾波方法，這一具有里程碑意義的濾波算法是采用傅里葉變換將干涉相位變換到頻率域平滑處理，再將平滑后的頻率域干涉相位做傅里葉逆變換回到空間域。經典Goldstein濾波是典型的干涉相位濾波方法，它在去噪與保持影像分辨率的效果較好，但在選取參數主觀因素較強。在2003年，Baran等[6]將Goldstein濾波的濾波參數根據兩張SAR影像的相干性系數相聯系，使之可以根據相關性的好壞自動地改變濾波參數，從而改變濾波強度，使得傳統濾波效果進一步提升。2019年，Hensley[7]用Goldstein與Werner濾波結合的方法來解決因長時間、長基線引起的對噪聲的影響，但該方法在噪聲復雜區域去噪效果不佳，使得在高噪聲區域濾波質量仍然不高。

為了更有效抑制噪聲復雜區域，并保持條紋密集區域的信息不被破壞，以達到濾波結果有利于解纏和提升干涉測量精度的目的，本文提出了一種融合頻譜細化和自適應Goldstein相位濾波的方法，將圖像轉換至頻率域后，通過線性調頻Z變換(CZT)的方法進行局部的頻率估計，提高計算的頻率分辨率，使得在高噪聲區域的頻譜得以細化以達到更好區分噪聲與實際有用相位信息的目的；通過自適應的方式，可根據相干影像的相關性改變濾波強度，以達到去噪與保留條紋密集區信息的兼顧。將本文方法與Boxcar濾波、非局部均值濾波(non-local means，NL-Means)和自適應Goldstein濾波進行對比，通過仿真實驗與實際數據驗證本文方法的有效性。

1 融合頻譜細化的自適應濾波原理

1.1 線性調頻Z變換頻譜細化算法原理

如果說N點的快速傅里葉變換是在Z平面的單位圓上的等間距取N個點，那么CZT則是Z平面螺旋線的周線上Z變換取等間距N個點[8]。CZT頻譜細化可以計算在N點中輸入數列為x(n)的給定一條路徑的Z變換，采用增加輸出點數，使得輸出點多余輸入點數就可以達到對指定頻譜細化的目的[9-10]。

假設采樣序列x(n)，n=0，1，…，N-1中，采樣頻率為fs，其中f1～f2為需要細化的頻譜條帶，對信號進行N點快速傅里葉變換，故有原有信號的頻率分辨率為Δf=fs/N，所選需要細化條帶中心頻率為f0=(f1+f2)/2，帶寬為fw=f2-f1。用X(z)來表示x(n)序列的Z變換，通過CZT算法就可以計算給定點Zk上的Z變換X(Zk)。

Zk=AW-k，k=0，1，…，M-1

(1)

式中：A=A0e-jθ0；W=W0e-jφ0；M為所要分析復數頻譜的采樣點數;j為虛數。其中，A0和θ0分別表示第一個采樣點Z0的矢量半徑的大小與相角；W0為Z平面螺旋線的伸展率；φ0表示相鄰采樣點間的角度差。根據式(1)所給的Zk值，推導可得Z變換X(Zk)，如式(2)所示。

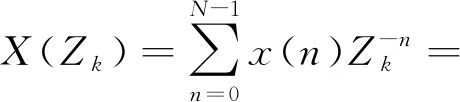
(2)

令

(3)

(4)

可得

(5)

令

(6)

可得

(7)

在實際過程中，頻帶點的采樣點數M需要根據整個頻譜的頻譜分辨率Δf′來確定，它們之間的關系滿足公式：Δf′=fw/(M-1)。由于此次頻譜分析在單位圓上進行CZT算法的實現，因此A0與W0取1，θ0=2πf1/fs，φ0=2πΔf′/fs。

1.2 自適應Goldstein算法模型

Goldstein濾波算法是基于一種傅里葉變換的自適應濾波方法，將干涉相位轉換至復數形式，有效避免干涉相位圖在相位跳變處的影像，并在空間域進行處理濾波。其濾波算法過程[11-13]如下所示。

將干涉相位圖(x，y)轉換為復數形式的矢量空間E(x，y)，如式(8)所示。

E(x，y)=exp(φ(x，y))=cos(φ(x，y))+j·sin(φ(x，y))

(8)

選定合適濾波窗口大小，對E(x，y)進行二維快速傅里葉變換到頻率域Z(u，v)(其中u，v表示空間頻率)，并進行Goldstein濾波處理得到H(u，v)，如式(9)所示。

H(u，v)=S{|Z(u，v)|}α·Z(u，v)

(9)

式中：S{}為濾波平滑算子；α(0≤α≤1)為過濾器參數。當過濾器參數α=0時，不對其進行平滑濾波，當α的值過大時，濾波結果將會在相位跳變密集區過度濾波，使得精度下降。為了提高濾波效果，α的取值將根據兩張SAR影像的干涉相關系數，即α=1-r(0≤r≤1)。最后將經過濾波后的頻率域H(u，v)做二維快速傅里葉逆變換得到濾波后的結果。

這種使用相干性系數作為過濾器的平滑參數的特點是在相干性好的區域可以防止過度濾波，從而使干涉圖的分辨率降低，而在相干性差、噪聲多的區域增強濾波效果，達到對噪聲更好的過濾。

1.3 基于融合CZT頻譜細化的自適應濾波方法

由于傳統的頻域濾波方法在相對較低的頻域分辨率中分辨有用信息與噪聲的能力有限，為了能夠將這些噪聲復雜區域進行良好的濾波，同時保持干涉條紋緊湊區域的信息不被破壞，本節結合了上述CZT頻譜細化和自適應Goldstein濾波方法的特點，提出了CZT頻譜細化與自適應濾波相融合的方法。通過CZT頻譜細化的方法細化相位干涉頻率域的頻率分辨率，區別噪聲頻率與有用信息相位的頻率界限，并根據兩幅干涉的主副影像在噪聲復雜區域相關性較差，條紋密集區有著較高相關性的特點改變濾波參數的大小實現在噪聲復雜區域濾波良好的同時盡量減小對條紋密集區細節的丟失。其具體算法流程如下。

步驟1：首先將干涉相位轉換至矢量空間，使得跳變的不連續的相位變成連續的復相位數據，通過式(8)得到復干涉相位E(x，y)。在一個復干涉相位的小窗口內(窗口大小為Na×Nr)，相位變化的坡度可以認為是近似相等的常數，即通過快速傅里葉變換將復干涉相位轉換到頻率域中的僅有的一個主頻，這個主頻對應的相位如式(10)所示。

φ(m+p,n+q)=2πp·fa+2πq·fr+φ(m,n)

(10)

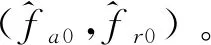
步驟2：針對復干涉相位轉換到頻率域中的頻譜峰值作為主瓣始點進行頻譜細化，通過式(1)至式(7)，對計算窗口的方位向與距離向取3×32個采樣點做CZT變換，對主頻譜瓣進行32倍采樣估計，可得式(11)。

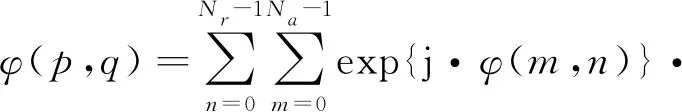
(11)

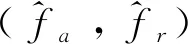
(12)

則在這個小窗口內的線性相位細化頻譜如式(13)所示。

ih=0，1，…，Nr-1

(13)

步驟4：根據細化后的復干涉相位頻帶做自適應濾波(式(14))。

(14)

根據上述步驟原理，其流程圖如圖1所示。

圖1 本文干涉相位濾波方法流程

2 實驗方案與評價指標

2.1 實驗方案

通過仿真實驗與實測數據來驗證本文提出的方法。其中，仿真數據來源于MATLAB軟件中peak函數生成的理想干涉圖(圖4(a))與添加了真實SAR影像噪聲的仿真干涉圖(圖4(b))，用來模擬真實噪聲的影響。實測數據來源于將Sentinel-1A的單視復數影像通過ENVI軟件中的SARscape模塊通過裁剪、配準等預處理所產生的干涉圖(圖7(a))。為了驗證本文濾波方法的有效性，將本文方法與Boxcar、NL-mean和自適應Goldstein濾波方法作對比，從目視結果、相位殘差點數量、相位導數標準差以及仿真實驗誤差的角度進行分析。實驗方法流程如圖2所示。

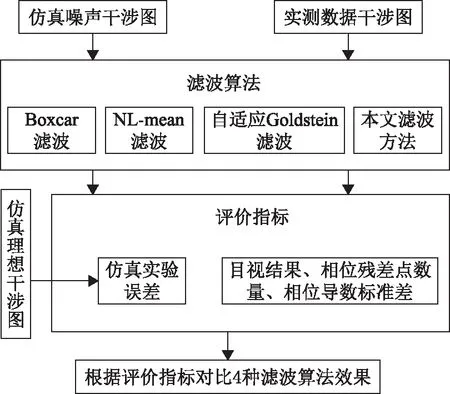
圖2 實驗方案流程

2.2 評價指標

為了更好地對比相位濾波效果，本文除了在目視效果上作對比外，還加入了相位殘差點與相位導數標準差作為對比依據，并且在后續的仿真實驗中對比了這幾種濾波方法的誤差效果。

相位殘差點的多少將直接影響相位解纏的質量，濾波后相位殘差點的數量越少，對相位解纏的效果越有利，其解纏的精度越高[14-15]。

相位導數標準差是評價干涉圖質量的有效方式，其值越大，說明干涉效果越差。

3 實驗結果分析

3.1 仿真實驗

為了更準確地對比實驗結果，本節使用仿真模擬干涉相位來對比本文濾波方法和其他3種相位濾波的提升效果。本小節仿真模擬相位圖由MATLAB軟件的peaks函數生成，大小為512×512，如圖3(a)所示。模擬真實SAR影像噪聲的仿真干涉相位圖如圖3(b)所示。圖3(c)至圖3(f)是4種濾波結果圖。通過這4幅濾波結果圖，可以較為明顯地判斷出Boxcar濾波與NL-mean濾波去噪效果較差，自適應Goldstein濾波與本文方法濾波效果較好。為了更好地顯示4種濾波方法在條紋密集區的濾波效果，圖3(g) 至圖3(j)給出了4種方法在圖上標出的條紋密集區濾波結果放大圖。可以看出，本文方法在去噪效果與干涉密集條紋保持情況相較于其他3種濾波方法更好。

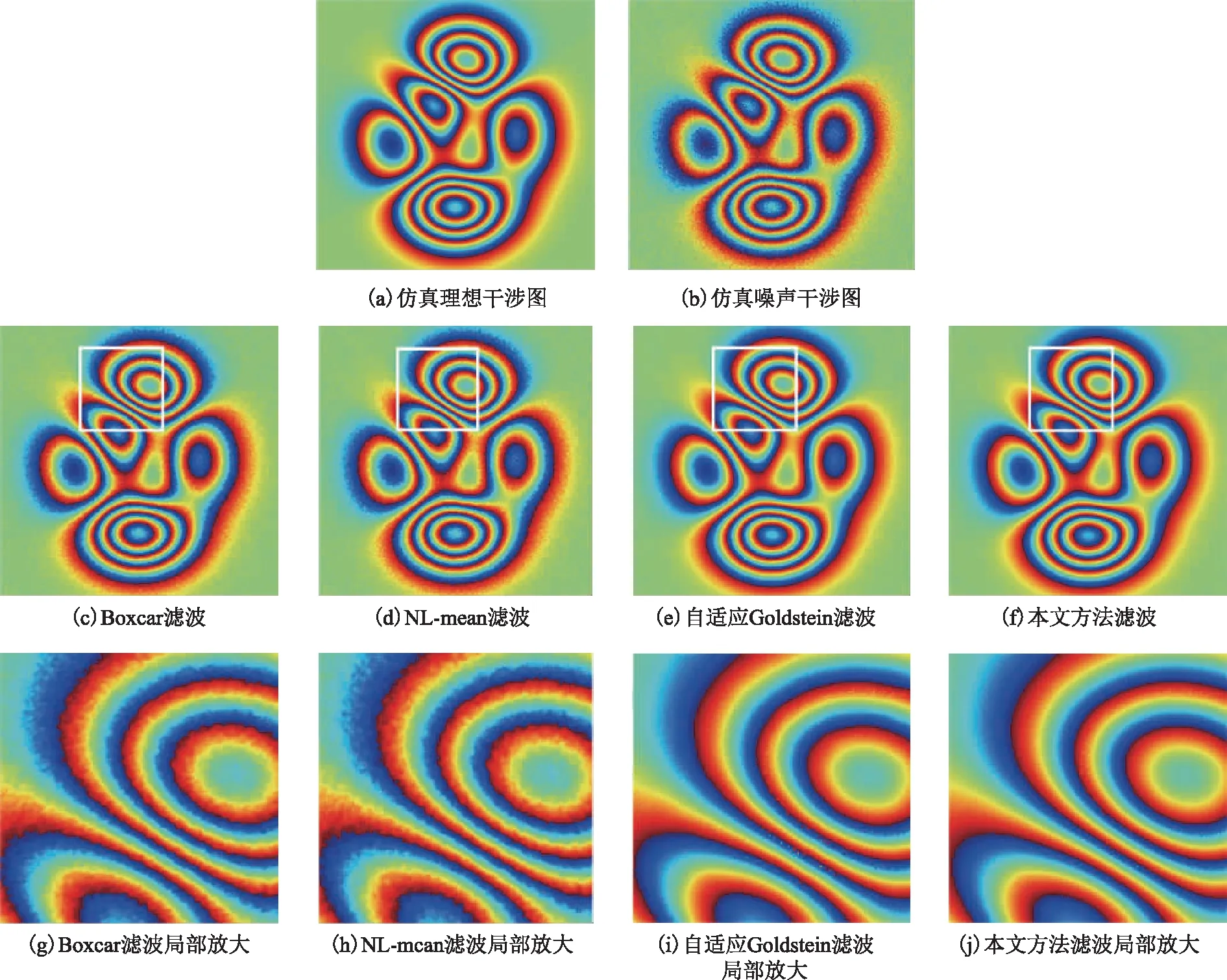
圖3 仿真數據及模擬干涉相位圖濾波結果與條紋密集區濾波放大圖

此外，通過對比4種方法濾波結果的相位殘差點數(表1)，不論在全局區域還是條紋密集區域，本文研究的濾波方法明顯少于另外3種濾波方法，這也意味著該方法更有益于后續的相位解纏階段。圖4表示4種濾波方法的相位導數標準差統計情況。從相位導數標準差統計圖可看出本文研究方法相對于其他3種方法的相位導數標準差值的數量更靠近0，表明本文方法濾波結果的干涉圖質量相較于另外3種方法有不同程度的提升。從仿真實驗的誤差統計圖(圖5)可以看出，這4種濾波方法的誤差結果都呈現近似正態分布，而本文濾波方法在全局區域和條紋密集區的誤差所呈現的正態分布尖峰更高，證明本文方法在全局區域與條紋密集區域的濾波精度相較于其他3種方法有所提升，證明本文方法在去噪效果與保持條紋密集區域的信息上有更好效果。

表1 不同濾波方法結果的相位殘差點數量

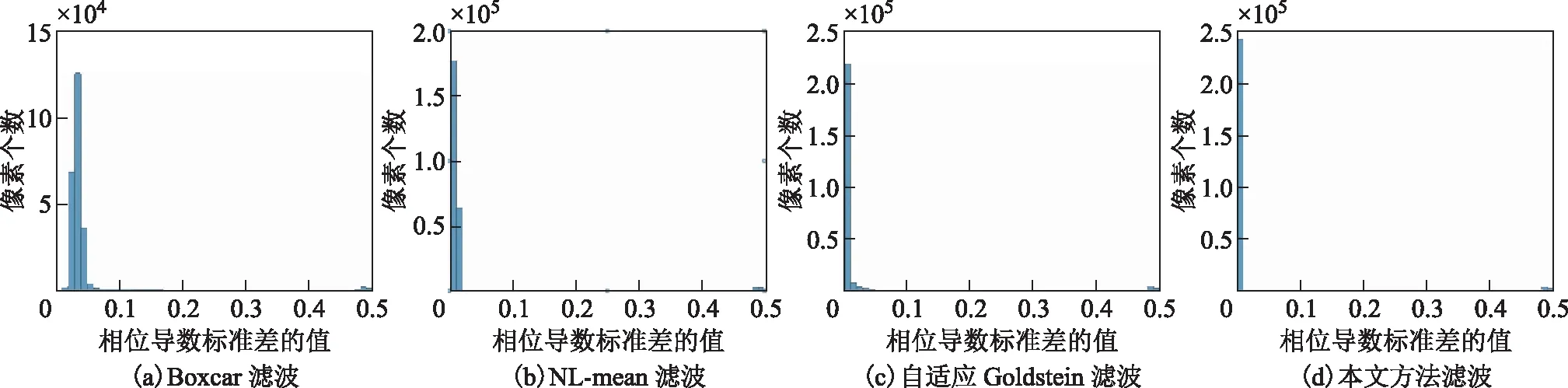
圖4 4種濾波方法的相位導數標準差統計對比

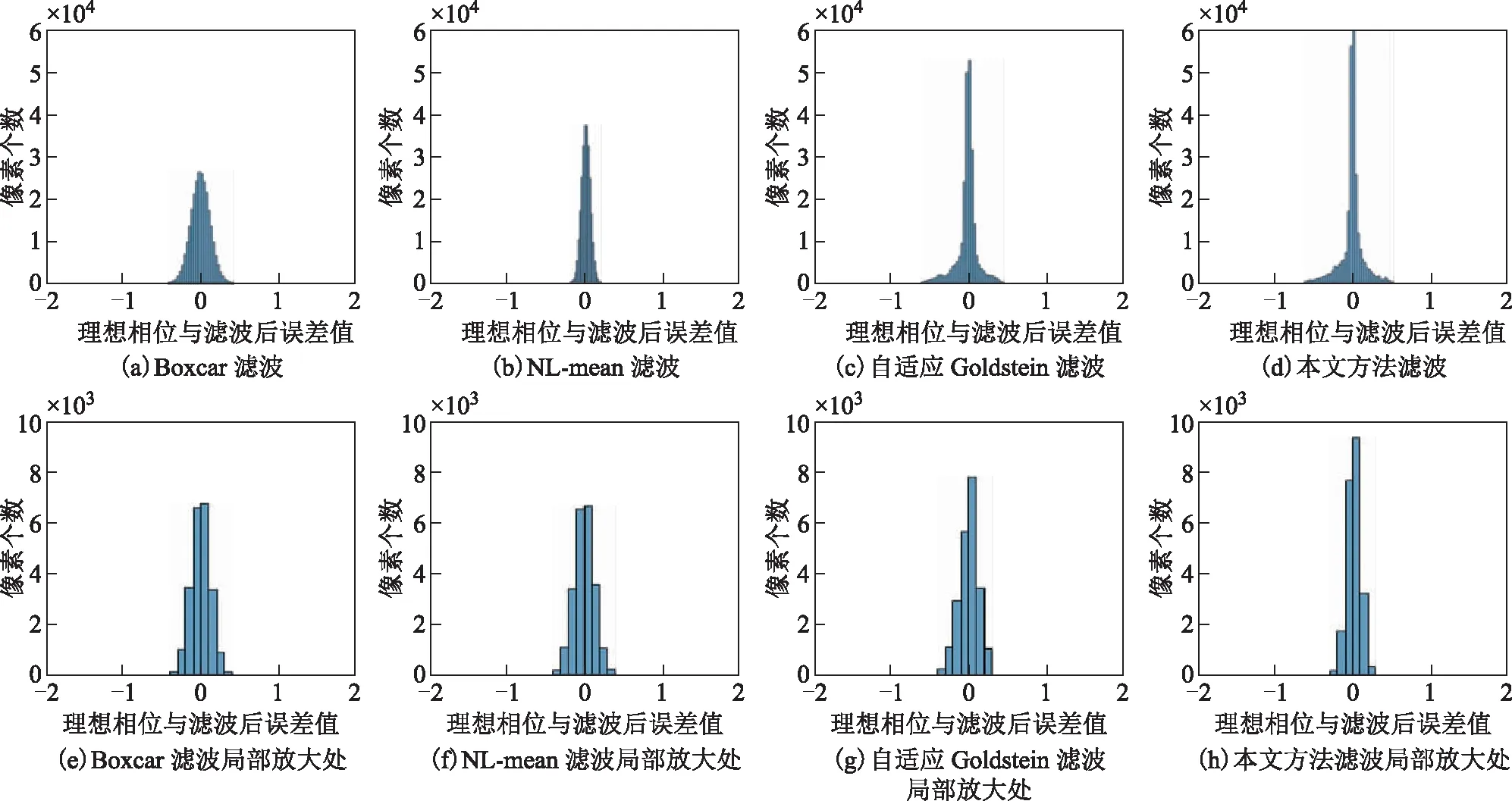
圖5 4種濾波方法結果及條紋密集區濾波結果的誤差統計對比

3.2 實測數據實驗

本節使用的實測數據為哨兵1號SAR影像數據，選用2018年12月12日與2018年12月23日福建省泉州市某區域裁剪后的影像進行干涉，截取了600像素×600像素大小的干涉區域作為實驗對象。所選區域為多山且林區密集，干涉形成的噪聲較為復雜且干涉條紋比較密集有利于進一步驗證本文算法良好的去噪能力與保持條紋細節信息的能力。圖6為實測數據和4種方法的濾波結果。可以看出，在相同大小13×13的濾波窗口條件下，Boxcar與NL-mean濾波方法在去噪能力上較弱，自適應Goldstein濾波無法較好地保持條紋細節，而本文濾波方法在良好去除噪聲的同時保證了緊湊條紋信息能夠較好保存。此外，在表1所示不同方法濾波結果所含殘差點數目中，本文濾波結果后的殘差點最少，更利于相位解纏。圖7和圖8分別對比了4種方法的相位導數標準差及其統計圖，本文濾波方法由于相位導數標準差值更多地趨向于0，因此，本文濾波方法優于其他3種濾波方法。

圖6 實測數據和4種濾波方法結果

圖7 實測數據和4種濾波方法干涉結果的相位導數標準差圖對比

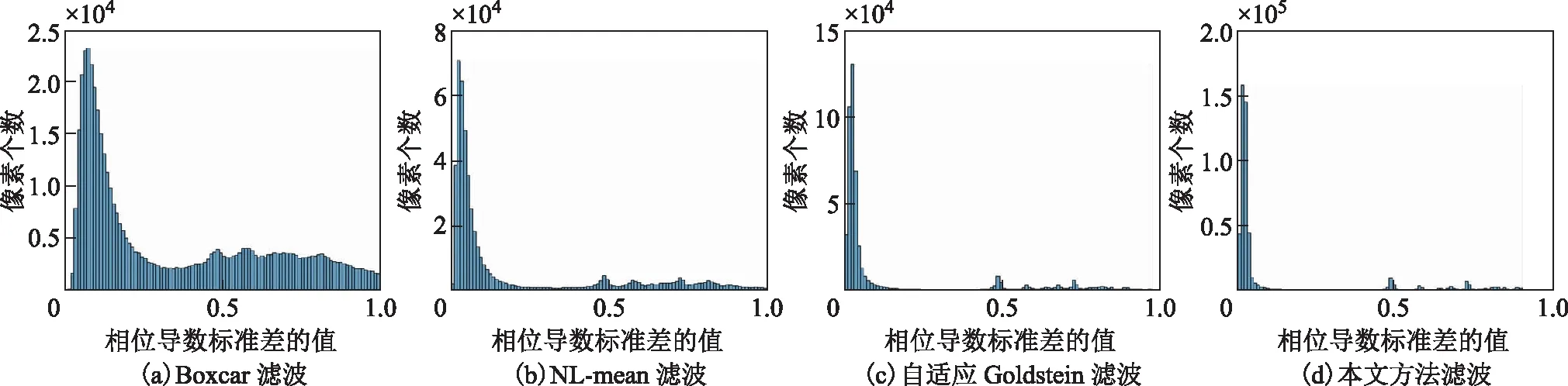
圖8 4種濾波方法干涉結果的相位導數標準差統計圖對比

4 結束語

本文將頻譜細化原理與自適應濾波相結合，通過提升圖像變換為頻率域的頻率分辨率的方式，更好地區分干涉相位中的噪聲信息來提升濾波效果與濾波質量，在保證良好的去除噪聲能力的同時又保證了條紋細節不被破壞。通過仿真實驗與實測數據，用本文方法與Boxcar濾波、非局部均值濾波以及自適應Goldstein濾波方法作實驗對比，在相位殘差點數量和相位導數標準差中，本文的濾波方法相對于其他3種方法效果更好。在仿真實驗誤差分析中，本文濾波方法對數據濾波后的準確性較高，有利于提高干涉測量的精度。通過以上實驗內容證明了本文濾波方法的有效性。