絕對重力測量中振動傳感器振動補償性能的分析*

文藝 伍康 王力軍

(清華大學精密儀器系，精密測試技術及儀器國家重點實驗室，北京 100084)

絕對重力測量的精度主要受振動噪聲的限制.振動補償是一種簡單可行的振動噪聲處理方法，它通過傳感器探測振動噪聲來對測量結果進行修正.現階段對于不同傳感器的振動補償性能缺乏系統的分析與評估，僅停留在應用階段.本文從理論出發分析了傳感器性能對補償效果的影響，并通過實驗評估了不同振動環境下不同傳感器的振動補償性能.實驗結果顯示，采用低噪聲地震計的振動補償效果主要受帶寬和量程的限制，在安靜環境下可實現優于百微伽的單次測量標準差，但補償效果隨振動噪聲高頻成分的增強而降低，在動態環境下地震計則受量程限制而無法工作.采用加速度計的振動補償效果主要受分辨率的限制，在復雜和動態環境下均可實現毫伽量級的單次測量標準差.本文為振動補償技術應用于絕對重力測量提供了振動傳感器選型的理論和實踐依據，有望為振動補償技術的進一步發展提供技術支撐.

1 引言

地表重力加速度(g，常用值9.8 m/s2)的精密觀測結果廣泛地應用于地球物理學、計量學、大地測量學等領域[1-3].重力加速度絕對值的測量被稱為絕對重力測量，通過絕對重力儀來實現.激光干涉式絕對重力儀是目前應用最廣、精度最高的絕對重力測量工具[2-4].它以穩頻激光器和銣鐘分別作為長度基準和時間基準，通過干涉儀測量真空中物體做自由落體運動的軌跡，再對自由落體軌跡進行二次擬合來得到g值，可實現μGal (1 μGal=10—8m/s2)量級的測量不確定度[5，6].其測量誤差主要來自地面振動噪聲[7]，綜合考慮噪聲強度、頻率和相位因素的影響，對于復雜振動環境下的振動補償應用，消除或衰減 0.1—100 Hz 范圍的噪聲所造成的干擾是實現優于毫伽量級重力測量不確定度的關鍵[8-13].

隔振和振動補償是絕對重力測量處理振動噪聲的兩種主要方法[14，15].其中，振動補償是通過傳感器探測振動噪聲來修正測量值，具備強振動環境下開展絕對重力測量的應用潛力，但振動傳感器的性能制約著振動補償效果.目前常用于振動補償的振動傳感器有兩類:寬頻帶地震計和加速度計.寬頻帶地震計分辨率較高，其帶寬約在0.01 Hz—80 Hz，相對于振動補償應用較窄，對于高頻振動存在探測信號失真問題，而且量程較小通常不適用于較強振動噪聲及移動平臺環境;加速度計測量分辨率比寬頻帶地震計要低，但帶寬可達數百Hz 甚至kHz 量級，量程一般都超過 ± 2 g，可以適應較強振動噪聲及移動平臺環境.以卡爾加里大學、中國計量院、清華大學、浙江大學和法國巴黎天文臺等為代表的研究機構采用地震計實現了實驗室環境下的振動補償，補償后單次測量標準差達到百微伽量級[15-20].以蘇黎世聯邦理工學院、法國航空航天實驗室、浙江工業大學等為代表的研究機構則應用加速度計進行了野外或移動平臺的振動補償，補償后單次測量標準差達到毫伽量級[21-24].然而上述振動補償技術的研究并未系統分析和比較傳感器的性能指標對振動補償效果的影響.

本文通過理論分析和對比實驗研究了振動傳感器主要性能指標在不同振動環境下對絕對重力儀振動補償精度的影響，提供了振動傳感器選型的理論依據和實驗驗證，有望為發展振動補償技術、提高補償精度提供技術支撐.

2 振動補償

2.1 原 理

目前典型的激光干涉式絕對重力儀是基于馬赫-曾德爾干涉測量原理來測量下落棱鏡的自由落體運動軌跡，如圖1(a)所示.激光器準直后發出的光束經分光鏡分為兩路，透射光為參考光，反射光為測量光.測量光經下落棱鏡和參考棱鏡反射后與參考光重合并發生干涉，干涉條紋的數量反映自由落體過程中測量光的光程變化.因此，干涉測量得到的自由落體軌跡Sm實際上是下落棱鏡相對參考棱鏡的運動軌跡.假設下落棱鏡做理想自由落體運動S，下落測量過程中參考棱鏡受噪聲干擾而產生的運動為N，則理想自由落體運動軌跡S與實際測量軌跡Sm的關系為

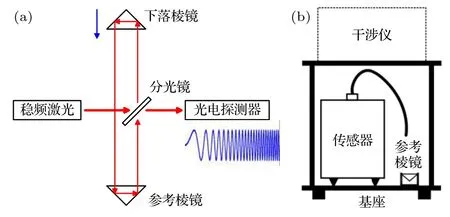
圖1 (a)激光干涉測量和(b)振動補償的原理示意圖Fig.1.Schematic diagram of (a) laser interferometry and(b) vibration correction.

由此可見，參考棱鏡的運動N給測量軌跡Sm引入了誤差.振動補償的原理就是利用傳感器測量參考棱鏡的運動N來對干涉測量軌跡Sm進行修正，系統結構如圖1(b)所示.由于傳感器的敏感結構和參考棱鏡是不同的物體，傳感器測量所得運動Nm并不等價于參考棱鏡的真實運動N，兩者之間存在偏差 ΔN.采用傳感器探測信號Nm對測量軌跡Sm進行修正，修正后的軌跡Sc為

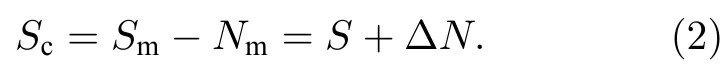
由此可見，傳感器探測誤差 ΔN也是修正后的軌跡Sc與理想自由落體軌跡S間的誤差.因此如何減小探測誤差 ΔN，使傳感器的探測信號Nm盡可能接近參考棱鏡真實運動N是實現高精度振動補償的關鍵.

傳感器輸出Nm和參考棱鏡真實運動N的關系如圖2 所示，兩者之間的傳遞函數關系G(s)可以表示為

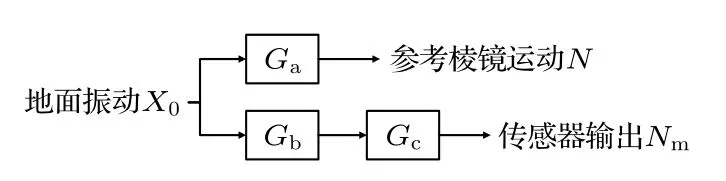
圖2 傳感器輸出與參考棱鏡運動的關系Fig.2.Relationship between the output of sensor and the motion of reference retro-reflector.

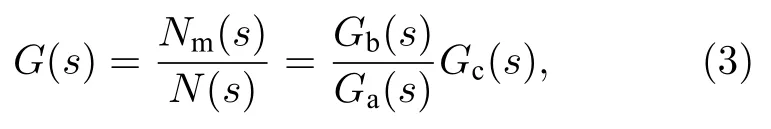
式中Ga為地面振動X0到參考棱鏡運動N的傳遞函數，Gb為地面振動X0到傳感器輸入的傳遞函數，Gc為傳感器的傳遞函數.要實現高精度的補償效果，需要從傳感器輸出的Nm盡可能準確地還原參考棱鏡運動N.由(3)式可知有兩個關鍵因素:一個是振動補償算法，其作用在于盡可能準確地求解傳感器輸出和參考棱鏡運動間的傳遞函數G(s);另一個是傳感器的性能，其作用在于使傳感探測到的信號Nm盡可能得準確，從而可以結合補償算法還原出參考棱鏡的真實運動N.

2.2 算 法

補償算法的關鍵在于求解傳遞函數G(s).目前已有不少關于補償算法的研究，由于真實傳遞函數G(s) 的復雜性，現有補償算法均將G(s)進行了合理的簡化[15-17，25].本文采用課題組已有的振動補償算法[16]，該算法將傳遞函數G(s)簡化為增益延時模型Gs(s)，傳感器輸出Nm與參考棱鏡運動N的關系可表示為

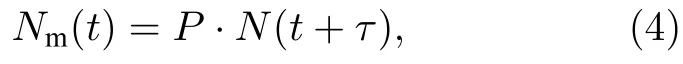
其中，P為增益，τ為延時，兩者均為待確定的未知參數.

參數求解過程分為兩步:先利用相關分析法求解延時τ，取傳感器信號所得位移的擬合殘差和干涉測量軌跡的擬合殘差相關系數最大處的延時作為延時參數τ;再采用遍歷法以單次補償后的擬合殘差標準差最小為優化目標，確定增益P的最優解，最終求解出補償傳遞函數Gs(s)[16].

2.3 振動傳感器

振動傳感器的性能也是影響補償精度的關鍵因素之一，其中分辨率、帶寬和量程是需要重點關注的性能指標.由于傳感器的輸出通常包含有效信號和自噪聲，若有效信號的強度小于自噪聲則會被噪聲淹沒，導致傳感器輸出信噪比過低而無法使用.因此要實現目標精度的振動補償，首先傳感器的分辨率(即儀器自噪聲)要優于目標精度，如優于5—10 倍及以上.當傳感器的分辨率滿足目標補償精度的需求時，其補償效果仍會受傳遞函數帶寬的影響，這主要是由傳感器的真實傳遞函數與補償算法所用的簡化模型不等價所導致.在傳感器傳遞函數的—3 dB 帶寬附近以及帶寬外，其幅值隨頻率的變化為非線性衰減，不滿足增益延時模型中增益為常值的特性;其相位隨頻率的變化也不能近似為線性關系，不滿足增益延時模型中延時環節的特性.因此若傳遞函數的帶寬較小，無法保證在目標頻帶內滿足補償算法所用模型的簡化條件，則無法從傳感器輸出得到真實準確的參考棱鏡運動，從而影響補償精度[13].此外，傳感器的量程決定了傳感器能工作的測量范圍，在振動幅值超出量程的測量環境下，傳感器無法進行有效的振動補償.

綜上所述，傳感器的分辨率和帶寬是保證補償精度的基礎，而量程則主要限制振動傳感器所能承受的最大振動環境.此外，長期穩定性等其他特性也會影響傳感器輸出信號的精度，從而影響補償效果.

3 實驗系統與過程

3.1 實驗系統

實驗采用基于振動補償的絕對重力測量系統，主要由真空腔、干涉儀和振動補償裝置組成，如圖3(a)所示.采用超低頻垂直隔振器的T-3 型高精度絕對重力儀常用于安靜環境下的高精度絕對重力測量，其合成不確定度為7 μGal.圖3(b)為T-3 型高精度重力儀在西安中心地震臺24 小時的重力測量結果，統計不確定度為2.7 μGal.因此測量精度更優的T-3 型高精度重力儀可用于驗證傳感器的振動補償效果.

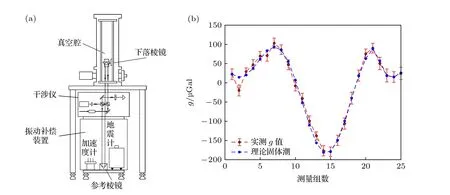
圖3 (a)基于振動補償的T-3 型絕對重力儀示意圖;(b) 基于超低頻垂直隔振的T-3 型高精度絕對重力儀在西安中心地震臺的重力測量結果.Fig.3.(a) Schematic diagram of T-3 type absolute gravimeter using vibration correction;(b) tidal gravity measurement conducted by T-3 type high-precision absolute gravimeter using ultra-low frequency vertical vibration isolator at Xi’an Seismological Station.

振動補償裝置采用地震計和加速度計兩種振動傳感器，均緊密放置在參考棱鏡附近.實驗選用的地震計包括英國Guralp 公司生產的 CMG-3ESP型地震計和中國港震公司生產的CS60 型地震計，加速度計是航天科工三院33 所研制的JN06D 型高精度石英撓性加速度計.地震計和加速度計的相關性能指標如表1 所列.傳感器輸出信號的采集通過NI 公司的24 位數據采集卡PCI-4462 來實現，實驗中采用200 kS/s 的采樣率同時采集4 個通道的輸入信號.

表1 振動傳感器性能指標Table 1.Characteristics of vibration sensors.

3.2 實驗過程

為進行不同振動環境下不同傳感器補償效果的對比評估，重力儀系統在3 種振動環境下比較地震計和加速度計的補償性能，如圖4 所示.第一種振動環境為中國計量院昌平園區內重力實驗室的隔離地基，實驗裝置如圖5(a)所示.昌平計量院的地基穩固性高，整體振動小于0.1 μg (RMS 值，帶寬 ＜ 10 Hz)[26]，承辦過2017 年國際重力比對，是一個非常安靜的振動環境，因此將該地基稱為安靜地基.第二種振動環境為清華大學焊接館實驗室內的地基，實驗裝置如圖5(b)所示.該實驗室地基不是隔離地基，距離地鐵13 號線約800 m，距離校內主要道路約10 m，受校內施工、人流車流密集往來等因素的影響，地面振動較昌平地基大且高頻成分增加，對于絕對重力測量來說屬于嘈雜的振動環境，因此將該地基稱為嘈雜地基.第三種振動環境為放置在清華大學焊接館實驗室內的被動萬向懸架，重力儀系統固連在萬向懸架的內框架中，如圖5(c)所示.萬向懸架的穩固性遠不如地基，除了地面振動噪聲外，萬向懸架上的儀器自振動也大大增加，該環境下振動噪聲接近或超過地震計量程，僅采用加速度計進行振動補償.

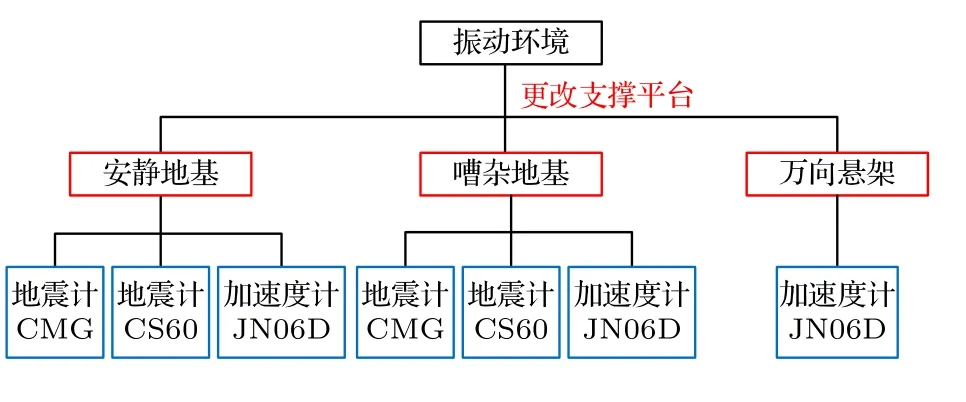
圖4 實驗采用的不同振動環境類型Fig.4.Different cases of vibration environments for experiments.

振動補償實驗包括兩個步驟:第一步是采集數據，在重力測量的同時采集多個傳感器的輸出信號和干涉條紋采集的觸發信號;第二步是數據后處理，將傳感器輸出信號利用觸發信號與下落測量軌跡進行大致的同步標定，再分別采用不同傳感器數據進行振動補償，并比較不同傳感器的補償結果.在不同振動環境下重復上述實驗操作，比較同一振動環境下不同傳感器補償性能的優劣以及不同環境下同一傳感器補償性能的變化.

4 實驗結果與分析

4.1 實驗結果

振動補償結果如表2 所列，表中計算系統偏差所用的真值g0為FG5(合成不確定度2 μGal)或A10 (合成不確定度10 μGal)在相應測量點的標定值.圖6 和圖7 中的誤差帶表示95%置信水平下的擴展不確定度，k為擴展不確定度的包含因子[26].

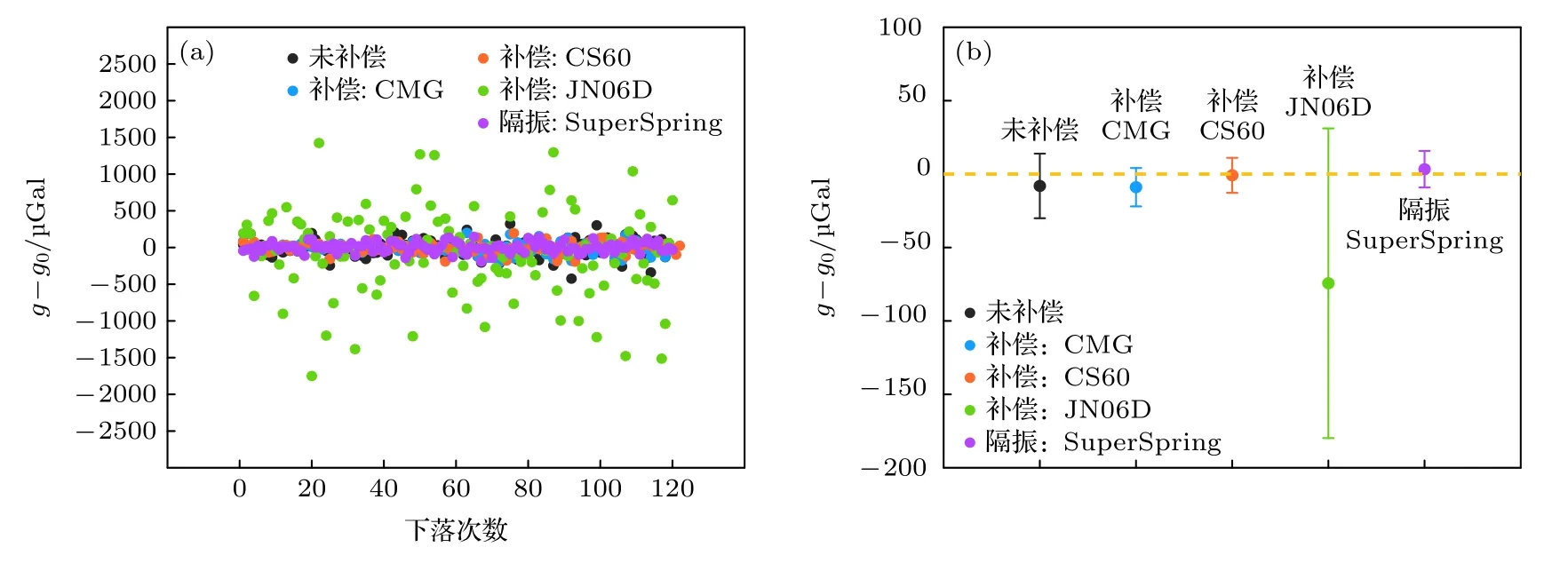
圖6 安靜地基上的結果對比 (a)逐點分布;(b)含誤差帶的均值(k=2)Fig.6.Comparison of results on the quiet ground:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

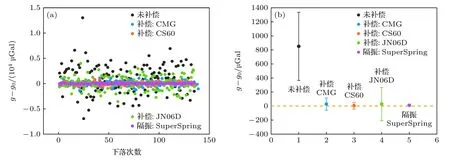
圖7 嘈雜地基上的結果對比 (a)逐點分布;(b)含誤差帶的均值(k=2)Fig.7.Comparison of results on the noisy ground:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

對于安靜地基的振動環境，如圖6 所示，兩款地震計的補償性能接近，補償后的單次測量標準差均為70 μGal 左右.采用JN06D 型加速度計補償后的單次測量標準差則由補償前的120 μGal 增大至578 μGal.

對于嘈雜地基的振動環境，如圖7 所示，采用地震計和加速度計補償后的系統偏差和單次測量標準差都得到明顯改善.采用CS60 型地震計、CMG 型地震計和JN06D 型加速度計補償后的單次測量標準差分別為289，511 和1374 μGal.然而兩種地震計的補償效果均不如隔振，且相比安靜地基環境的補償效果有所下降，其中帶寬更小的CMG型地震計補償效果下降更明顯.

對于萬向懸架的振動環境，圖8 給出了JN06D型加速度計在下落過程中測得的振動加速度，幅值約為0.1 m/s2，頻率約為12 Hz.根據表1所列，這一振動幅值已經接近CMG 型地震計和CS60 型地震計的輸入限幅，因此在萬向懸架上并未采用地震計進行振動補償.而JN06D 型加速度計則補償效果明顯，如圖9 所示，補償后系統偏差由—1158 mGal 修正為—285 μGal，單次測量標準差由43 mGal 減小為3.3 mGal.

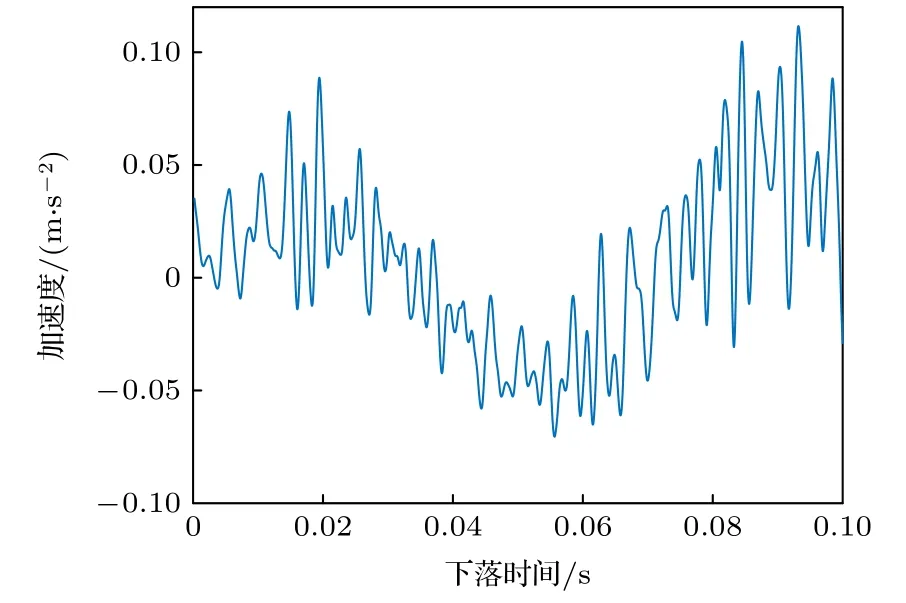
圖8 萬向懸架上JN06D 測得單次下落過程中的振動加速度Fig.8.Vibration acceleration measured by JN06D on the gimbal during a single drop.

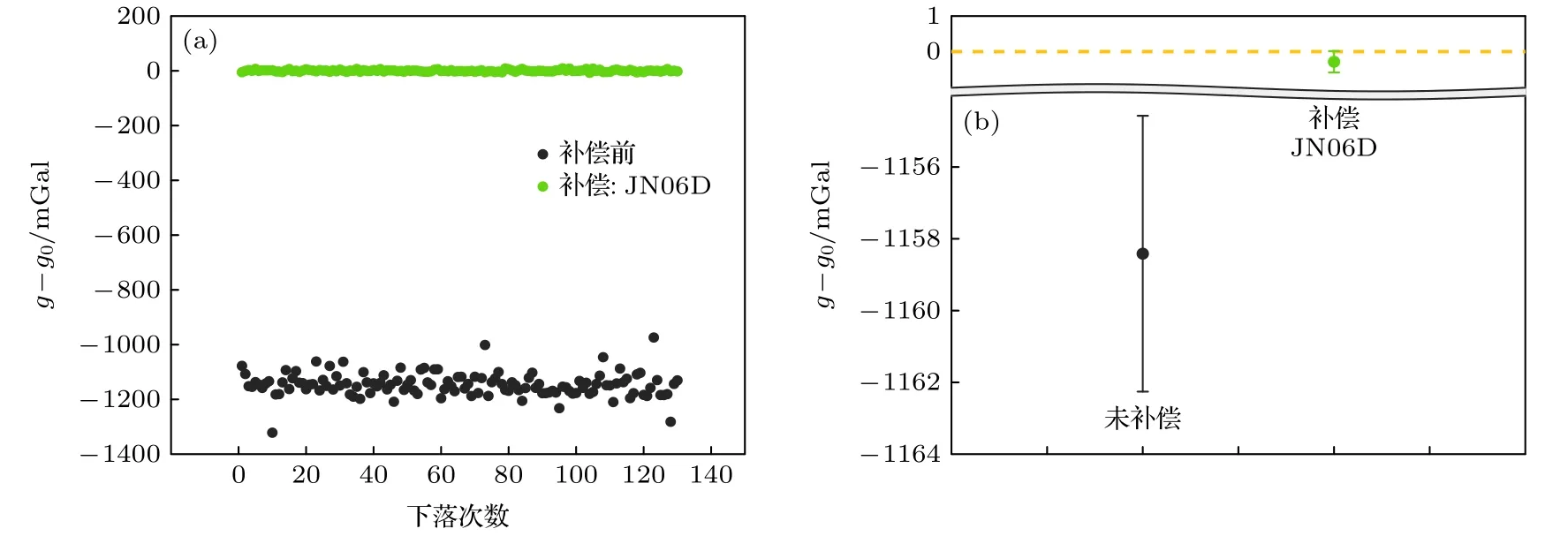
圖9 萬向懸架上的結果對比 (a)逐點分布;(b)含誤差帶的均值(k=2)Fig.9.Comparison of results on the gimbal:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

4.2 分析討論

本節根據單次補償情況來具體分析同一振動環境下不同傳感器的補償性能以及同一傳感器不同振動環境下補償性能的變化.

在安靜地基的振動環境下，補償前的原始擬合殘差幅值約為6 nm，主導頻率成分約為20 Hz，如圖10(a)所示.這表明安靜地基上參考棱鏡所受振動噪聲的幅值很低，且以20 Hz 左右的低頻噪聲為主，因此補償前的單次測量標準差較低.一方面這與安靜地基的地脈動噪聲更小有關;另一方面也與安靜地基對真空腔和參考棱鏡的物理隔離作用有關.重力測量過程中儀器產生的反沖振動通過地基傳導至參考棱鏡處，因此地基越穩固，對反沖振動的衰減越明顯，參考棱鏡所受振動幅值越小，且以低頻為主[11].在安靜地基上，兩款地震計的分辨率可實現對小振幅低頻振動噪聲的高精度探測.且主導振動噪聲的頻率范圍均位于兩款地震計帶寬內的響應平坦區域，有利于增益延時模型實現良好的補償效果.從圖10(a)和圖11(a)可以看出，CMG型和CS60 型地震計的探測位移擬合殘差和原始擬合殘差相關性很高，印證了地震計良好的振動探測性能和模型的有效性，因此補償后得到的擬合殘差低頻噪聲幅值衰減且更接近于白噪聲，測量結果也得到改善.由于兩款地震計的帶寬均滿足對低頻主導振動噪聲的探測需求，因此兩種地震計的補償效果接近.而JN06D 型加速度計的分辨率只有毫伽量級，對于百微伽量級的振動信號無法實現良好的探測.如圖12(a)所示，JN06D 所得探測位移的擬合殘差和原始擬合殘差相關性差，因此采用不準確的探測信號無法實現補償效果.

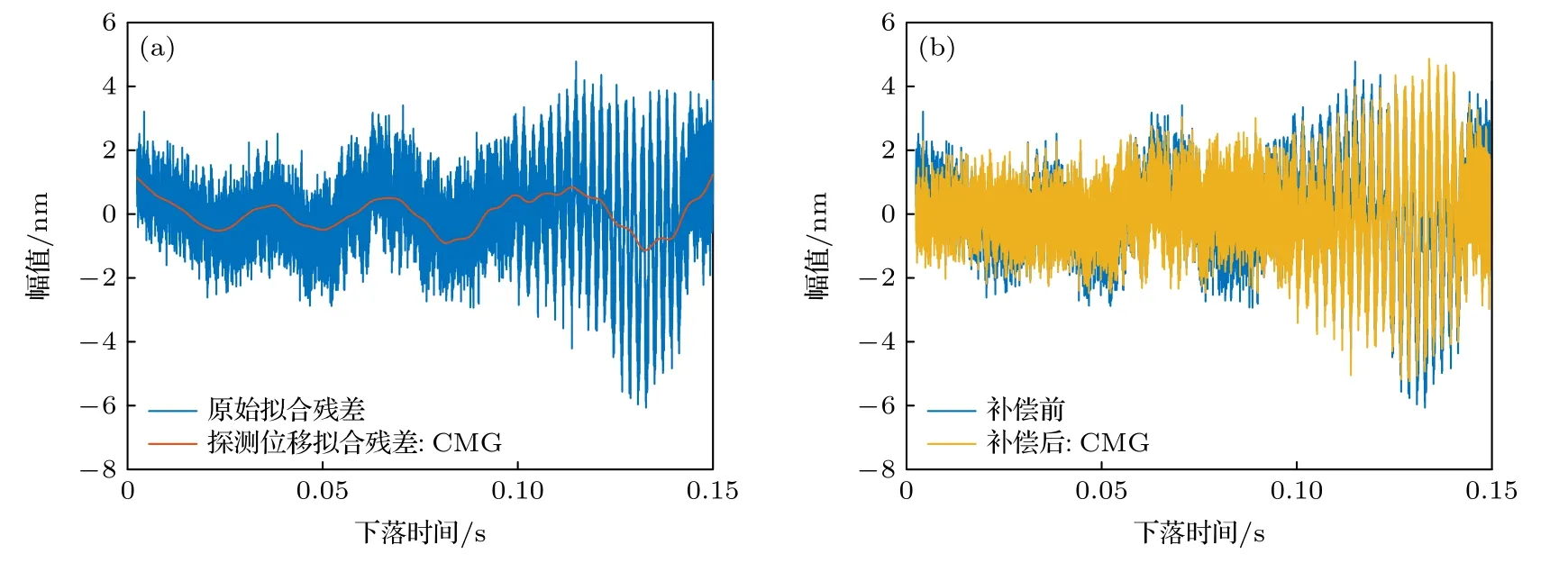
圖10 安靜地基上CMG 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.10.Correction for single drop using CMG data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

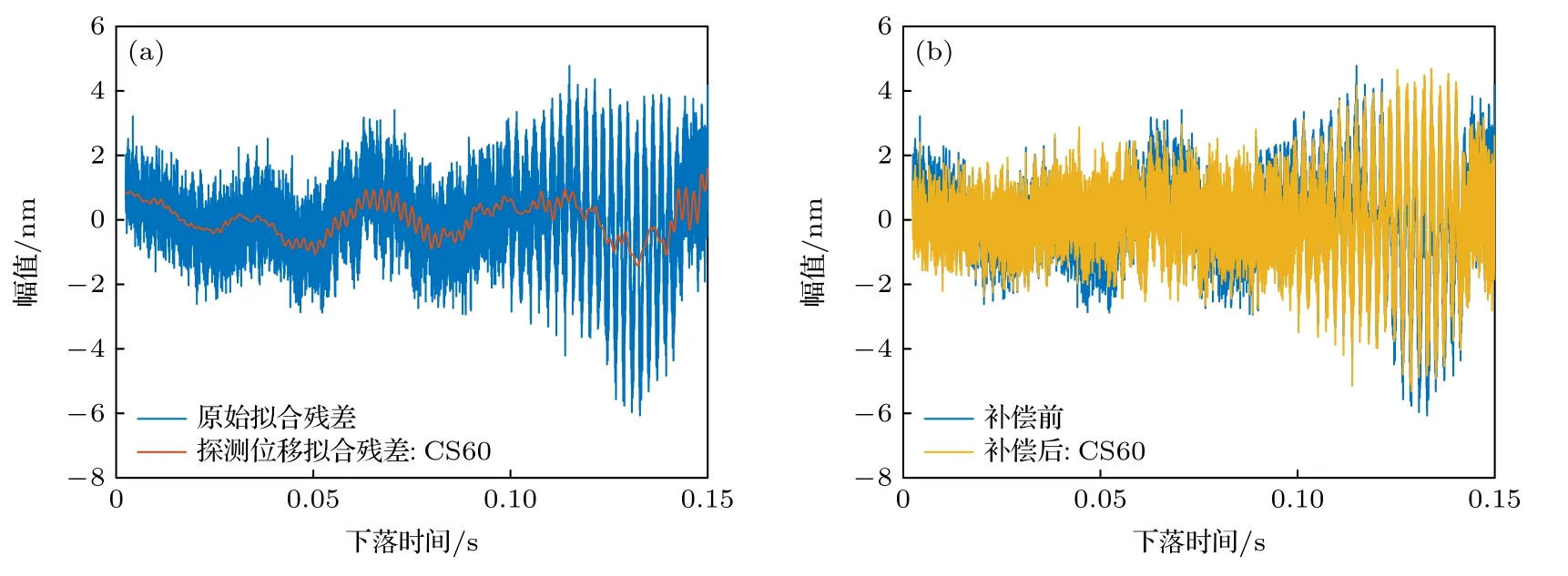
圖11 安靜地基上CS60 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.11.Correction for single drop using CS60 data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

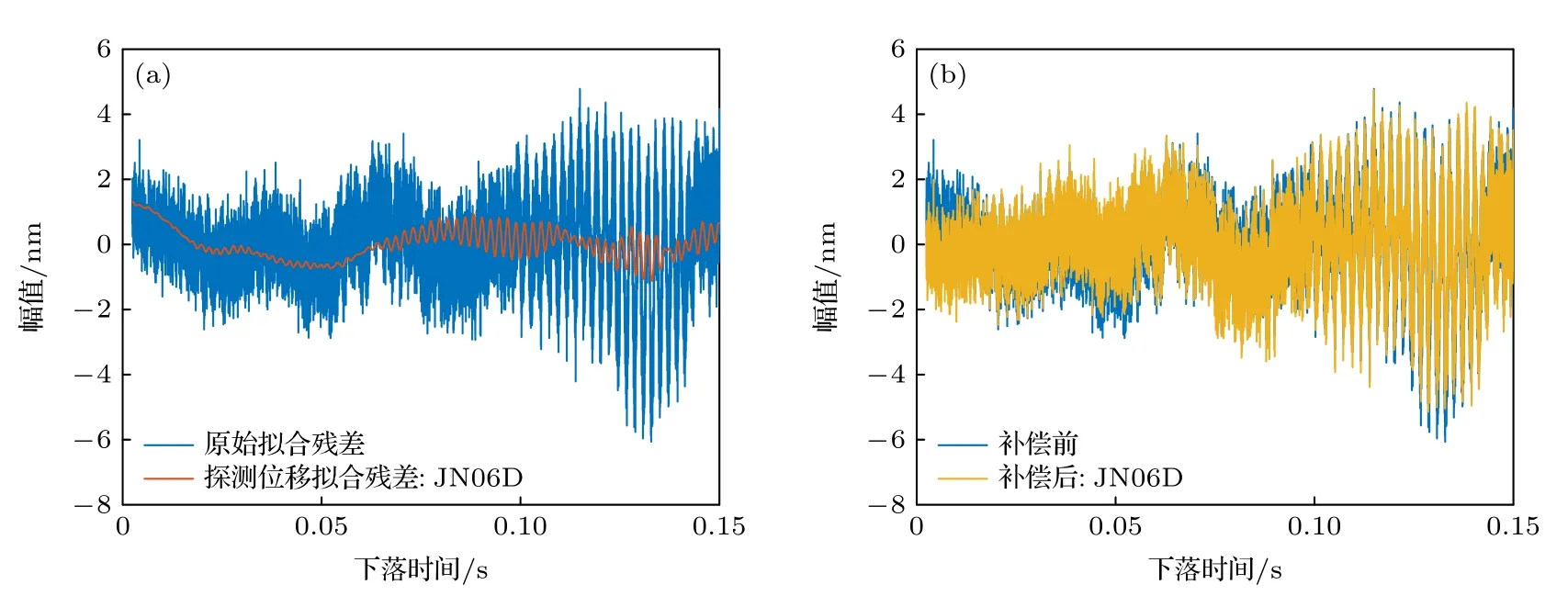
圖12 安靜地基上JN06 D 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.12.Correction for single drop using JN06 D data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

在嘈雜地基的振動環境下，地基的穩固性相比安靜地基下降，一方面噪聲源和噪聲強度增加，另一方面地基對反沖振動的衰減作用減小.從圖13(a)可以看出，原始擬合殘差的幅值約為60 nm，是安靜地基環境的10 倍，振動噪聲高頻成分明顯增加且幅值增強，因此補償前的單次測量標準差相比安靜地基環境增加，達到毫伽量級以上.對比圖13(a)和圖14(a)可知，盡管仍能有效探測振動信號，但兩款地震計都受帶寬限制出現了不同程度的高頻信號失真.其中帶寬更大的CS60 型地震計高頻失真程度較低，其探測信號相比CMG 型地震計包含更多的高頻細節，更接近真實振動，因此補償后的擬合殘差幅值更小，補償效果也更好.對于JN06D 型加速度計，其毫伽量級的分辨率可以實現該環境下振動噪聲的有效探測，高達kHz 的帶寬可避免高頻信號失真.如圖15(a)所示，JN06D 的探測信號擬合殘差與原始擬合殘差具有一定相關性，其中探測信號高頻分量很強，與真實振動接近，但低頻分量與真實振動的匹配度不如地震計高，因此加速計的補償效果不如地震計，這主要是受分辨率的限制.

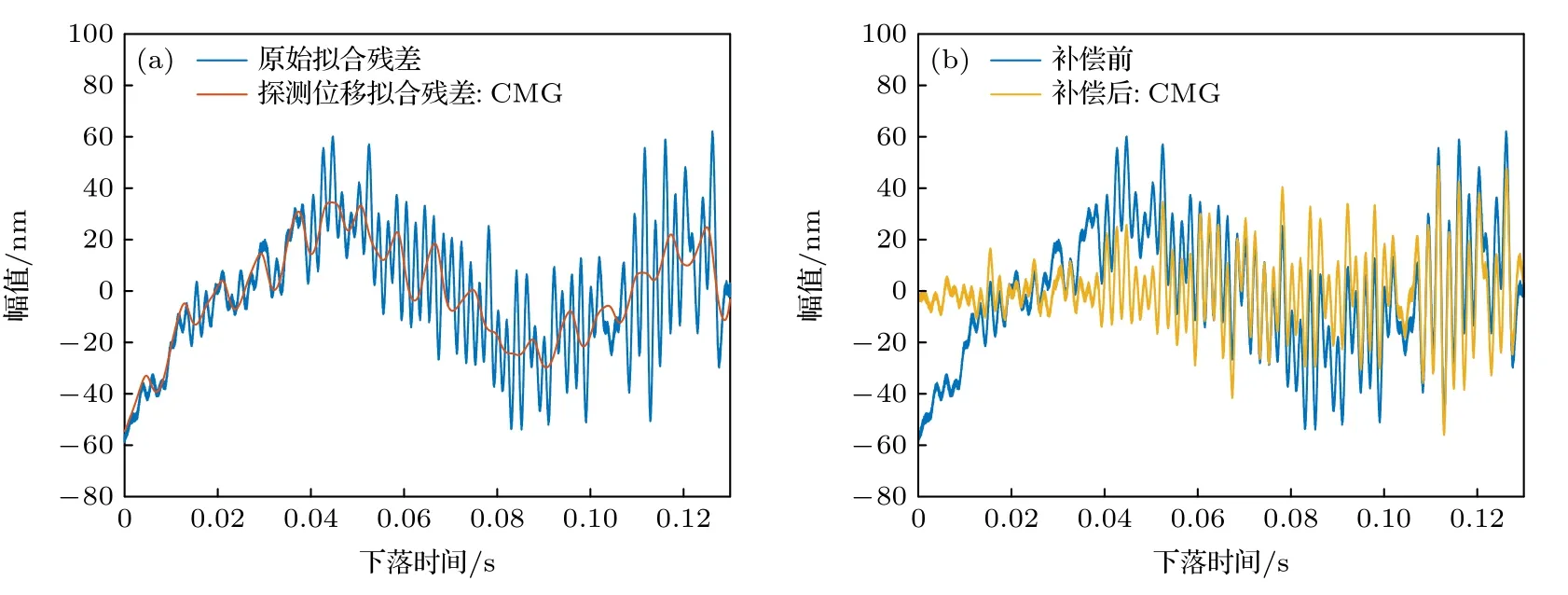
圖13 嘈雜地基上CMG 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.13.Correction for single drop using CMG data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

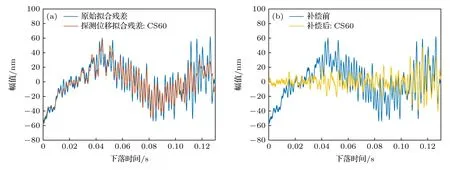
圖14 嘈雜地基上CS60 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.14.Correction for single drop using CS60 data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

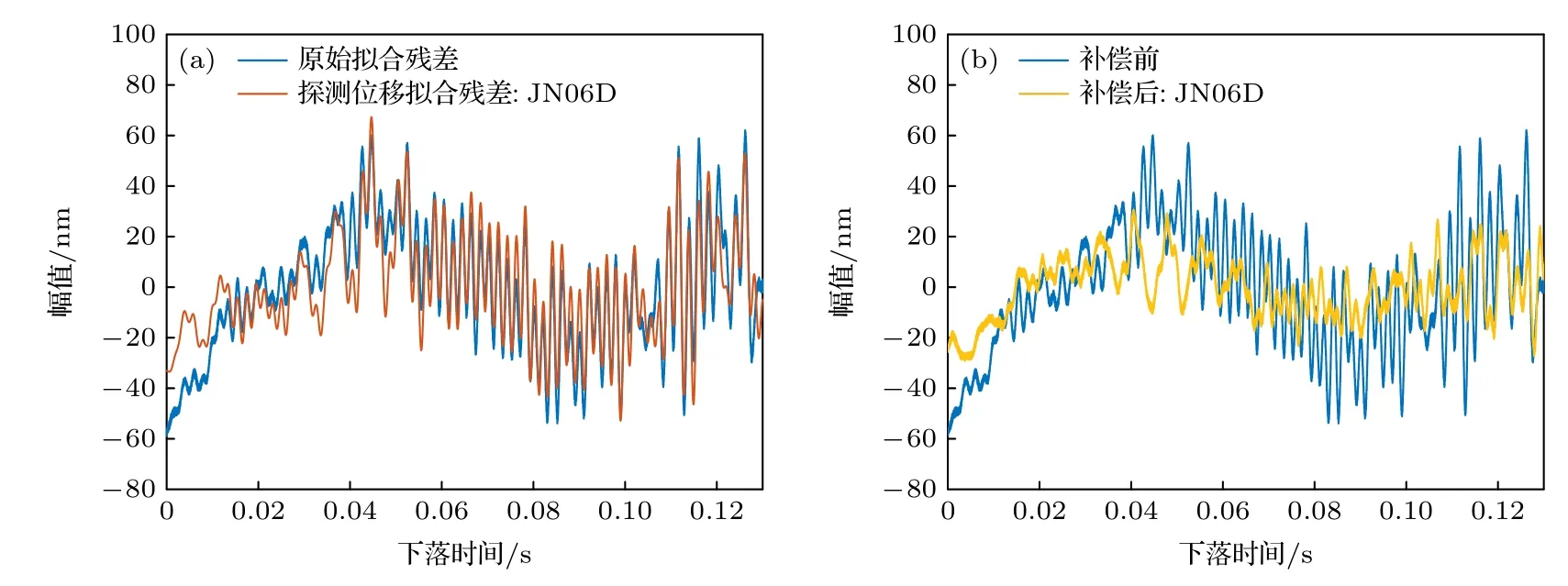
圖15 嘈雜地基上JN06 D 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b)補償前后擬合殘差對比Fig.15.Correction for single drop using JN06 D data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

對于采用萬向懸架作為支撐平臺的振動環境，由于萬向懸架的穩固性遠不如地基，因此萬向懸架上的振動噪聲在3 種振動環境下最大.圖16(a)中幅值高達5000 nm 左右的原始擬合殘差反映了萬向懸架上的高幅值振動噪聲.且該振動噪聲存在高度復現性，說明萬向懸架上的振動噪聲以重力儀系統測量過程中產生的反沖振動為主.在高強度振動環境下，JN06D 型加速度計的分辨率足以實現良好的振動信號探測，如圖16(a)所示，JN06D 的探測位移擬合殘差與原始擬合殘差呈現極高的相關性，補償后的擬合殘差大幅度衰減，補償后的系統偏差從—1158 mGal 修正到—285 μGal，單次測量標準差也從43 mGal 減小到3.3 mGal.因此動態性能更好的加速度計能在強振動環境下實現毫伽量級的單次測量標準差.

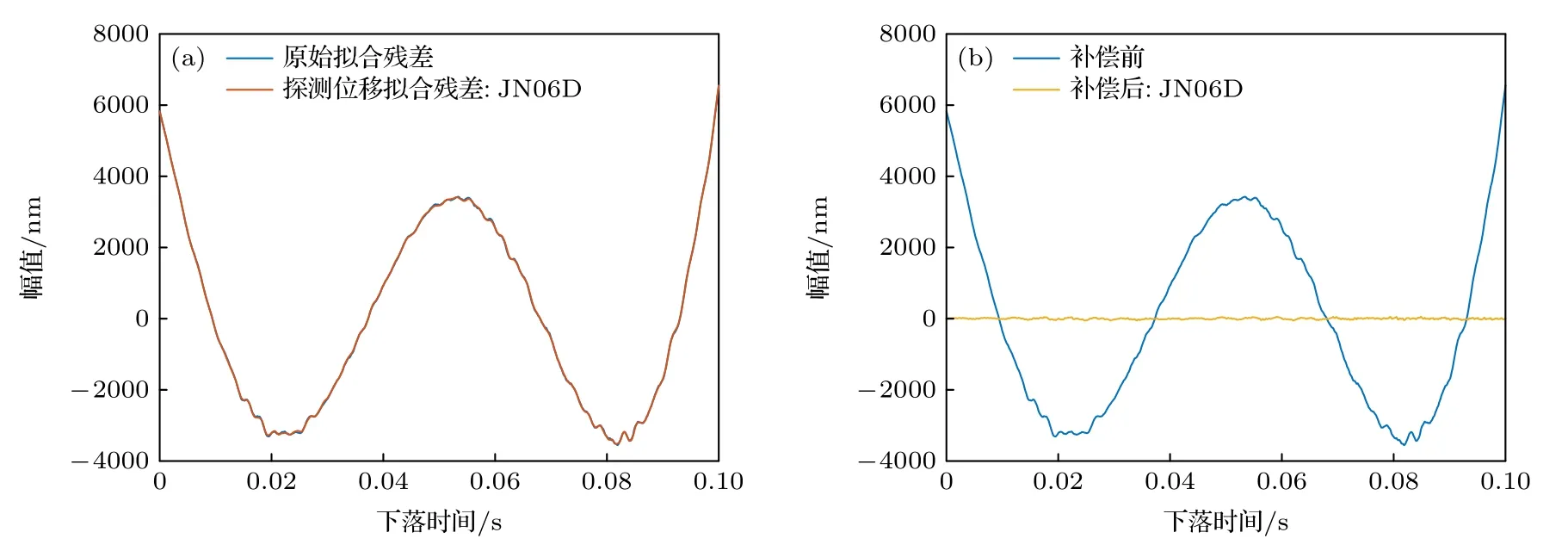
圖16 萬向懸架上JN06 D 單次補償的情況 (a)原始擬合殘差與探測位移擬合殘差對比;(b) 補償前后擬合殘差對比Fig.16.Correction for single drop using JN06 D data on the gimbal:(a) Residuals of the measured trajectory Sm，and the measured vibration noise Nm;(b) residuals of the measured trajectory Sm before and after correction.

進一步分析同一傳感器在不同振動環境下補償性能的變化.對于振動噪聲強度小、頻率低的安靜地基測量環境，CMG 型和CS60 型地震計的分辨率和帶寬基本上能滿足單次測量標準差優于百微伽的補償需求，且可以實現接近隔振性能的補償效果.但隨著振動噪聲高頻成分的增加，受帶寬限制，地震計會出現高頻信號探測失真現象，從而導致補償效果下降[13].因此在嘈雜地基的測量環境下，CMG 型和CS60 型地震計的補償效果均明顯下降，由于CMG 的帶寬更窄，其補償效果下降更嚴重.由此可見，在分辨率滿足目標精度的前提下，傳感器帶寬也是影響補償效果的重要因素.因此，若要在較復雜的嘈雜振動環境下進一步提高地震計的補償性能，在保證分辨率的前提下可以考慮提高地震計帶寬，如采用數字后校正方法[13]或研制帶寬更高的地震計.而對于振動幅值超出地震計量程的萬向懸架測量環境，地震計將不再適用.另一方面，JN06D 型加速度計的優點是帶寬和量程大，動態性能好，基本上可以覆蓋現有野外甚至移動平臺重力測量的需求，但受限于其毫伽量級的分辨率.因此，對于以低幅值低頻率振動噪聲為主的安靜地基測量環境，加速度計受分辨率限制而無法實現單次測量標準差優于百微伽的補償效果.當振動噪聲強度增大至毫伽量級以上，加速度計可以實現有效的信號探測，補償后可以實現毫伽量級的單次測量標準差.而對于超出地震計量程的強振動測量環境，加速度計的補償效果更加明顯，補償后可以將系統偏差修正1000 mGal 以上，單次測量標準差也改善13 倍.因此，加速度計更適用于地震計無法工作的復雜或動態環境下實現毫伽量級的單次測量標準差.要進一步提高加速度計的補償性能，則需要在保證其帶寬和量程滿足需求的前提下提高分辨率，如清華大學研制的采用內置參考棱鏡的高分辨率傳感器[27].

最后，針對振動補償領域的傳感器選型或傳感器設計進行總結.根據前述分析，分辨率、帶寬和量程是需要重點關注的傳感器參數.因此，在選擇合適的傳感器時，首先應確認振動補償的應用環境，包括振動噪聲強度和頻率成分、以及支撐平臺的穩固性，針對應用環境制定合適的目標補償精度.然后根據應用環境的振動強度篩選量程滿足要求的傳感器，并選取分辨率優于目標精度的傳感器.最后，在分辨率和量程都滿足需求的情況下選擇在目標頻帶內傳遞函數更平坦的傳感器，這往往要求更大的帶寬.除上述主要參數之外，還可以結合傳感器的長期測量穩定性及外形質量等其他參數再綜合評估.

5 結論

本文理論分析了傳感器性能參數對振動補償的影響，并通過實驗對比研究了不同振動環境下不同傳感器的補償性能.實驗結果表明:在安靜地基環境下地震計可以實現單次測量標準差優于百微伽的補償效果，與隔振效果相當，而加速度計受分辨率限制無法實現有效補償;在嘈雜地基環境下受噪聲高頻成分增強的影響，地震計的補償效果下降，補償后的單次測量標準差增大至百微伽量級，其中帶寬更窄的地震計補償效果下降更明顯，加速度計則可以實現單次測量標準差達到毫伽量級的補償效果;在振動強度更大的萬向懸架環境下，地震計由于振動強度接近或超出其量程而無法工作，采用加速度計補償則可以將系統偏差修正1000 mGal 以上，將單次測量標準差改善13 倍達到毫伽量級.因此分辨率、帶寬和量程是影響傳感器補償性能的主要因素.其中地震計的補償性能主要受帶寬和量程的限制，多適用于有穩固地基的環境下實現單次測量標準差優于百微伽的補償效果，可以通過提高帶寬來進一步提高地震計的補償性能.加速度計的補償性能則主要受分辨率的限制，多適用于復雜或動態環境下實現毫伽量級的單次測量標準差，可以通過提高分辨率來進一步提高加速度計的補償性能.此外，結合地震計和加速度計的補償特性，本文還總結了振動補償的傳感器選型方法，為今后振動補償領域的傳感器選型和設計提供了理論依據.

感謝中國計量科學研究院的重力計量基準與精密測量實驗室和原子干涉重力精密測量實驗室分別為測試提供測試場地和CMG 型地震計.