多孔介質梁的精細積分模型及有限元仿真

陳正軒， 陸 靜，2， 潘 坤

（1.廣西科技大學， 廣西柳州 545006； 2.廣西汽車零部件與整車技術重點實驗室， 廣西柳州 545006）

0 引言

多孔材料具有很多良好的特性， 在各領域內得到了廣泛的應用。對多孔介質結構的振動特性進行研究分析，具有一定的理論和工程意義。在多孔介質材料的研究中，Biot 首先建立了分析多孔材料的經典理論[1]，在此基礎上，學者對經典Biot 理論進行了簡化，提出了更易理解應用的修正Biot 理論[2]。 結合Biot 理論，向宇等[3]建立了多孔介質矩形薄板的精細積分模型， 分析了多孔介質矩形薄板的的振動特性。 陸靜等[4]將Boit 理論與經典彈性薄殼理論相結合， 建立了一種分析流體飽和多孔旋轉薄殼振動的新模型。對于結構模型的求解，常用的有解析法[5]，解析求解方法僅能求解簡單的模型， 隨著有限元軟件的發展，數值解法在結構模型的研究分析中多有出現，數值方法對于中低頻段的問題求解較為精確， 對高頻段問題的求解則具有一定的局限性。

本文以多孔介質梁為研究對象， 考慮多孔介質梁內部骨架和流體之間的耦合作用， 導出多孔介質梁的一階常微分動力學控制方程， 利用精細積分方法對模型動力學控制方程進行求解， 與多孔介質梁的有限元仿真模型進行對比，驗證了多孔介質梁精細積分模型的有效性。

1 多孔介質梁控制方程的建立

如圖1 所示，梁的長、寬、高分別為a、l、h。 結構模型由多孔材料組成。

圖1 多孔介質梁示意圖

1.1 多孔介質梁的本構關系

基于 Biot 理論，不考慮y 方向的變形、內力和應力，得到多孔介質梁的本構關系[3]：

1.2 多孔介質梁固體骨架的幾何方程

1.3 多孔介質梁骨架的運動方程

式中，ρ11—固體相對密度；ρ12—固體和流體的耦合密度。

1.4 多孔介質梁內部流體的運動方程和本構方程

記u^f， w^f為內部流體沿x，z 向的位移變量，uf，wf為內部流體形心沿x，z 向的位移變量。對于多孔介質梁內部流體，其運動方程：

2 多孔介質梁的控制方程

2.1 多孔介質梁一階常微分控制方程

2.2 一階常微分控制方程求解

圖2 插值示意圖

式中，方程個數為10M，但未知狀態向量個數是為10（M+1），引入多孔介質梁模型的邊界條件，代入式（35），即可解出全部的未知狀態向量。

3 有限元仿真驗證

為了驗證本文建模和計算的正確性， 采用如表1 的主要參數，邊界條件為兩端簡支，在Abaqus 中對多孔介質梁進行仿真， 與采用齊次擴容精細積分方法在同樣參數條件下得到的多孔介質梁固有頻率進行比較， 如表2所示，由表中數據可知，采用精細積分法所得到的多孔介質梁的前五階固有頻率和Abaqus 中仿真得到的結果較為接近，誤差均小于10%，驗證了本文方法的正確性。

表1 多孔介質梁的材料參數

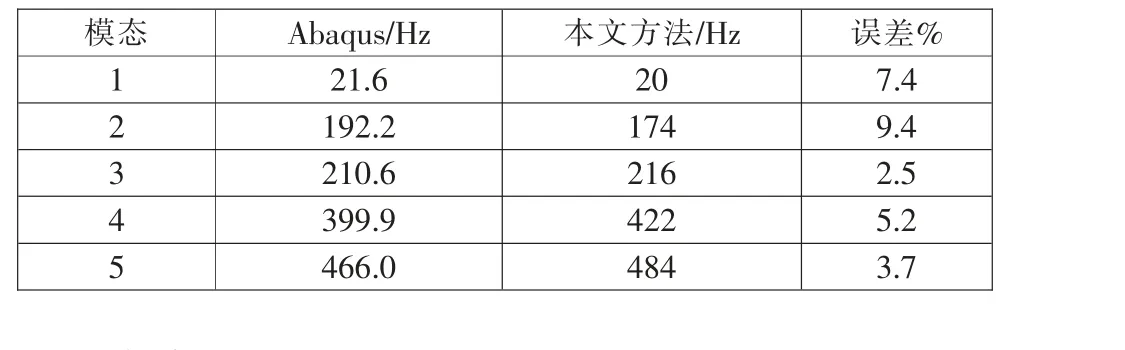
表2 多孔介質梁固有頻率的比較

4 結論

本文基于Biot 理論， 考慮了多孔介質梁的固體骨架和流體的耦合作用， 推導出了多孔介質梁的一階常微分控制方程，用精細積分法對控制方程進行了求解，得到多孔介質梁的固有頻率，與有限元仿真得到的結果比較，驗證了此建模方法的正確性，并且，此建模方法對模型邊界條件和頻段范圍有著較好的適用性。