基于改進PFV策略的雙車道連續元胞自動機模型*
趙子翔,彭勇,沙曉宇
(1.重慶交通大學 交通運輸學院,重慶 400074;2.華設設計集團,江蘇 南京 210002)
微觀交通流仿真模型是研究交通問題的重要手段,元胞自動機模型能有效描繪交通流運轉機理,探究道路中存在的交通問題。1992年,Nagel K.等將微觀交通流仿真與元胞自動機相結合,提出經典的NaSch模型。隨后大量學者在此基礎上進一步展開研究。但傳統元胞自動機模型將跟弛行為離散化,難以精細刻畫道路交通流狀態。為此,?znur Yeldan等提出采用連續元胞自動機模型研究高速公路隨機交通流,探究道路的連續性動態變化情況。基于該方法,彭勇等考慮多車影響的跟馳策略,構建了單車道連續元胞自動機模型。但現實中的道路由多條車道組成,行駛過程中車輛并非一直沿同一車道行駛,會出現換道行為,車輛跟弛不僅受到前后車的影響,還受到相鄰車道車輛的影響,不宜將單車道連續元胞自動機模型直接應用于多車道交通流仿真分析。對于多車道跟弛策略,Ge H.X.等提出一種結合反饋控制的雙車道跟馳策略,在跟馳策略中引入換道規則;夏冬雪等綜合考慮各種因素對駕駛行為的影響,提出考慮相鄰車道車輛和前方多輛車輛影響的雙車道跟馳策略;Ou H.等提出一種考慮車間通信的雙車道跟弛策略跟車模型。但在實際跟弛行為中,駕駛員通常會根據前后及相鄰車道多車信息進行跟弛決策。該文考慮多車信息的跟馳策略,結合換道規則,構建雙車道連續元胞自動機模型,并利用實際道路交通流數據對模型進行驗證。
1 雙車道連續元胞自動機模型
假設跟馳車隊在一條雙車道道路上行駛,將道路上的車輛視作元胞,車道路段長度L,元胞長度(車輛長度)l,路段的車輛承載力Nz=L/l。模型采用周期性邊界條件。雙車道元胞自動機模型仿真流程見圖1。
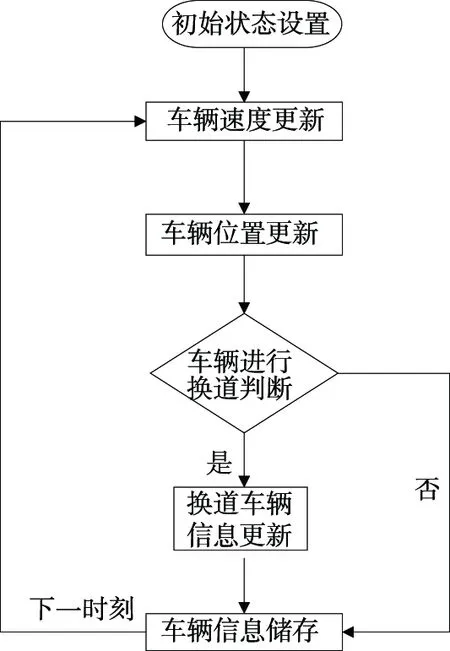
圖1 雙車道連續元胞自動機模型仿真流程
(1)初始車輛設置。每條車道車輛的初始位置和速度表達式如下:
xi,j(0)=(L/Na-l)rand(1)+
(L/Na)(i-1)+l
(1)
vi,j(0)=min(vmaxrand(1),di+1,j),
vi,j(0)>0
(2)
式中:xi,j(0)為每條車道上車輛的初始位置;i為車輛編號;j為道路編號;Na為道路上初始車輛數;rand(1)表示生成0-1的隨機函數;vi,j(0)為每條車道上車輛的初始速度;vmax為最大速度;di+1,j為當前車輛與前車的距離。
(2)速度更新。車輛速度更新規則如下:
vi,j(t+1)=min(vmax,di+1,j,vi,j(t)+
ai,j(t+1))
(3)
式中:vi,j(t+1)為車輛在t+1時刻的行駛速度;vi,j(t)為車輛在t時刻的速度;ai,j(t+1)為車輛在t+1時刻的加速度。
(3)車輛位置更新。更新規則如下:
xi,j(t+1)=xi.j(t)+vi.j(t+1)
(4)
式中:xi,j(t+1)為車輛在t+1時刻的位置信息;xi.j(t)為車輛在t時刻的位置信息;vi,j(t+1)為仿真步長為1 s時車輛行駛的距離。
(4)車輛換道。按換道策略進行換道決策。
2 跟馳和換道策略
2.1 跟馳規則
在PFV策略的基礎上,綜合考慮多車最優速度和前后車最優速度差的影響建立新的跟馳策略,表達式如下:
φV(Δxi+1,j(t))-vi,j(t)]+σΔvi,j(t)+
κ(V(Δxi+1,j(t))-V(Δxi,j(t)))
(5)
式中:V(·)為t時刻車輛i在車道j上的最優速度;Δvi,j(t)為t時刻車輛i在車道j上與前車的速度差;α、β、γ、φ、σ、κ為敏感系數。
采用Bando M.等提出的最優速度函數,表達式如下:
tanh(hc)]
(6)
式中:hc為安全距離。
選取文獻[9]中NGSIM高速公路數據,采用遺傳算法對跟馳策略參數進行標定。遺傳算法種群規模為50個,交叉概率為0.9,變異概率為0.2,迭代次數為200次。目標函數Fobj如下:
(7)
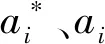
參數標定結果如下:α=0.521 4;β=0.542 3;γ=0.231 7;φ=0.123 1;σ=0.118 6;κ=0.098 4;Fobj=0.857 1。實測加速度與計算加速度對比見圖2,標定計算出的加速度與實際加速度有較好的擬合度,跟弛策略能較好地反映跟弛行為。
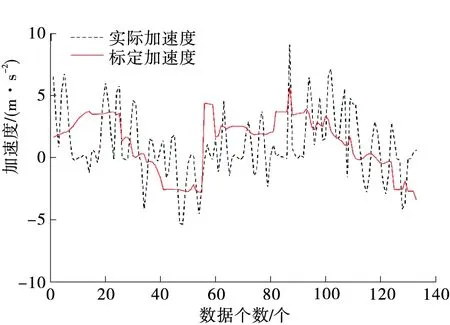
圖2 標定加速度與實際加速度對比
2.2 換道規則
實際道路中有強制換道和非強制換道2種換道行為。當車輛與前方車輛的距離幾乎小于安全距離時,車輛必須根據安全需要采取換道措施,這是一種強制換道行為。當車輛與前方車輛保持安全距離,但相鄰車道車輛較少時,可選擇是否換道,屬于非強制換道行為。據此制定變道策略(見圖3)如下:
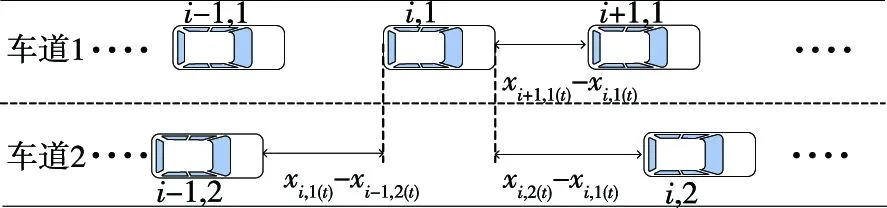
圖3 車輛換道示意圖
(1)車道1上車輛i與車輛i+1間距小于在時間步長Δt內車輛i行駛的距離時,車輛i產生換道意愿,即:
Dn<(vi,1(t)+ai,1(t)·Δt)·Δt
(8)
式中:Dn為車輛i與前車i+1之間的距離(m);vi,1(t)為車輛i當前的速度(m/s);ai,1(t)為車輛i當前的加速度(m/s2);Δt為單位時間。
(2)車道1上車輛i產生換道意愿后,當滿足車輛i與相鄰車道上前車的間距大于在時間步長Δt內車道1上車輛i行駛的距離與安全距離dsafe之和,且車輛i與目標車道上后車的間距大于在時間步長Δt內目標車道上后車行駛的距離與安全距離dsafe之和時,產生實際換道行為,即:
DQ>(vi,1(t)+ai,1(t)·Δt)·Δt+dsafe
DH>(vi-1,2(t)+ai-1,2(t)·Δt)·Δt+dsafe
(9)
式中:DQ為換道車輛與目標車道前車之間的距離(m);dsafe為車輛之間的最小安全距離(m);DH為換道車輛與目標車道后車間的距離(m);vi-1,2(t)為目標車道后車的速度(m/s);ai-1,2(t)為目標車道后車的加速度(m/s2)。
(3)根據2種換道行為的情況,加入換道概率ps,如果車輛與前方車輛保持相當大的安全距離,仍有可能產生換道意圖,然后重復第二步判斷是否存在換道條件進行換道。符合換道條件的車輛換道至目標車道,不符合換道條件的車輛不換道。當車輛橫向移動時,保持換道前的速度和加速度,然后根據跟馳規則更新行駛狀態。
3 仿真分析
3.1 仿真設置
仿真時長為5 000 s,2條車道初始車輛數相同(Na=100輛),車輛長度l=5 m,最大車速vmax=30 m/s,最大加速度amax=6 m/s2,換道概率ps=0.6。
3.2 仿真結果分析
如圖4所示,當交通流密度小于0.05 veh/m時,仿真結果較好;當交通流密度大于0.05 veh/m時,仿真結果比實際數據略高。總體來講,仿真結果與實際數據的擬合程度較好,說明基于上述跟馳-換道策略建立的雙車道連續元胞自動機模型合理,能用于交通流仿真。
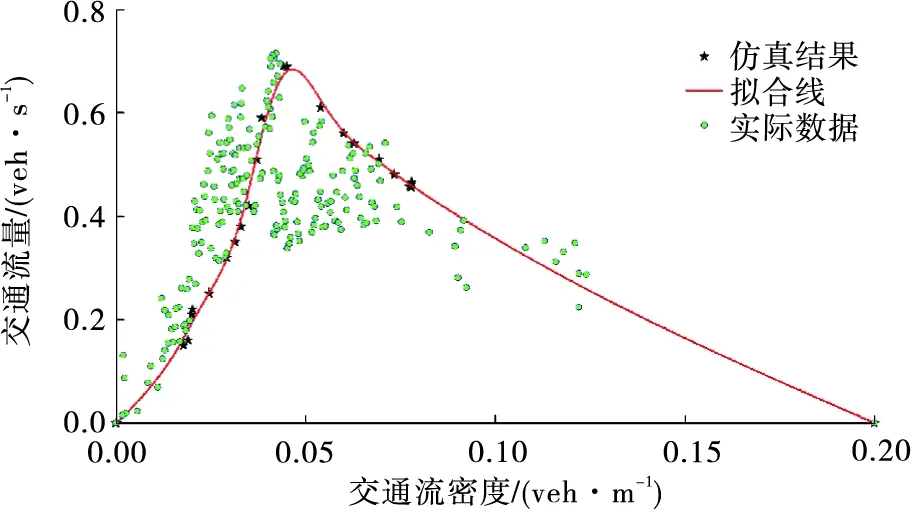
圖4 實際數據與仿真結果對比
圖5為車輛平均速度仿真結果。車輛根據跟馳策略和換道規則進行車速更新與調整,車道1與車道2車速相差不大,車速在26 m/s上下波動,道路總體情況較通暢,仿真效果與模型設置情況相符。
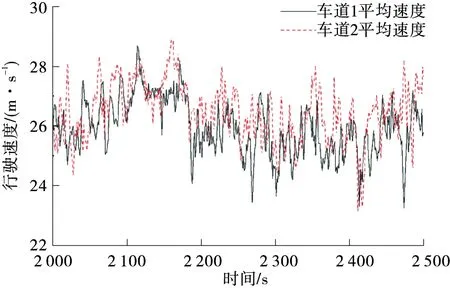
圖5 雙車道連續元胞自動機仿真平均速度
根據圖4仿真結果,分別選取交通流密度0.02、0.06 veh/m,比較分析在交通狀況良好和交通狀況較擁堵情況下雙車道交通流情況。圖6、圖7為不同交通流密度下仿真時空圖,圖中的點代表當前時刻車輛所處位置,可通過點的密集程度判斷道路的擁堵情況。
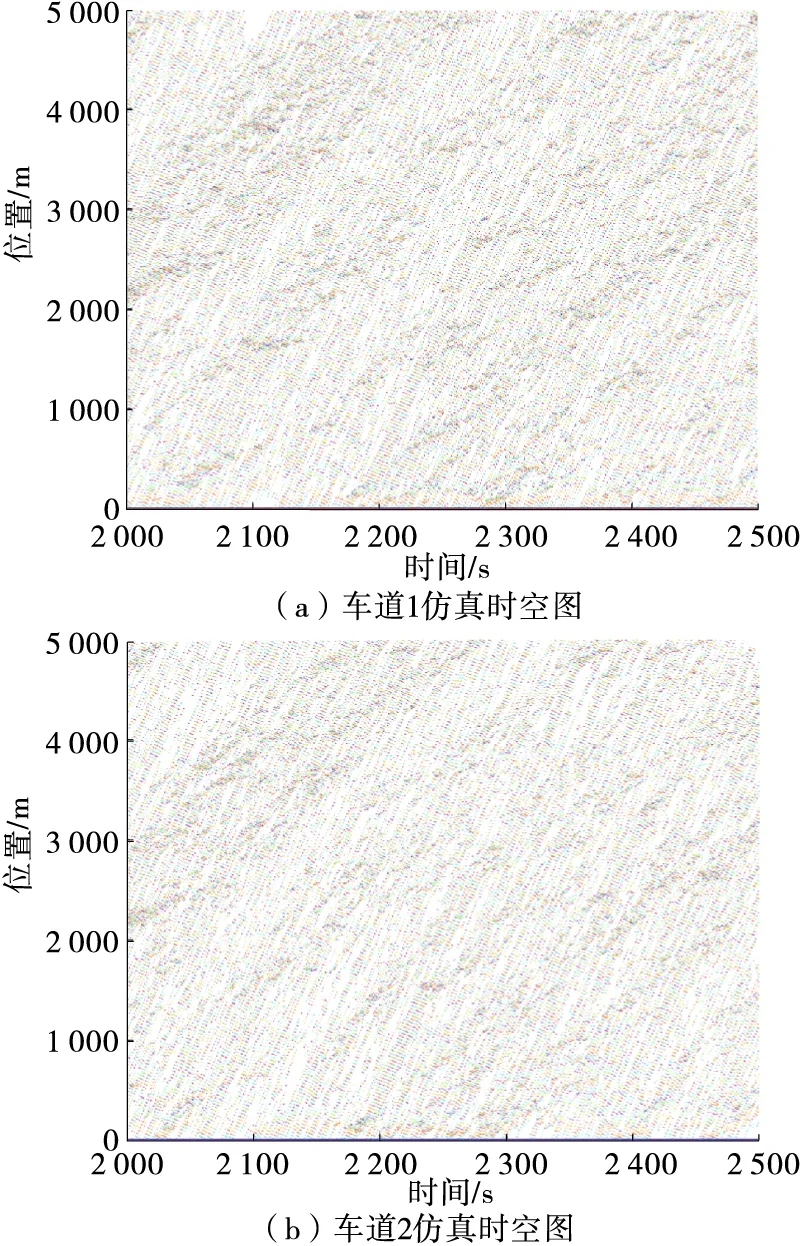
圖6 交通流密度為0.02 veh/m時雙車道時空圖
由圖6可知:交通流密度為0.02 veh/m時,車輛具有良好的行駛條件,車輛換道條件充分。仿真結束,統計2條車道通車情況,共有5 145 輛車通過路段終點。車輛換道會對目標車道上車輛造成一定影響,使目標車道上車輛出現一定減速,且減速情況向車流下游傳遞。車道1和車道2上車輛的平均速度分別為24.98、25.56 m/s,平均速度沒有發生明顯變化,整體通行較順暢。考慮跟馳與換道策略的仿真結果更符合實際情況。
由圖7可知:由于交通流密度增加,道路行駛狀況較差,換道條件不充足,極大減少了非強制換道次數,同時由于交通流密度較大,系統整體運行速度有所降低。在總仿真時長內,車道1、車道2上車輛的平均速度分別為11.82、11.51 m/s,與交通流密度為0.02 veh/m時相比,道路通行效率明顯下降,且由于車輛換道造成擁堵和延誤。在交通流密度較大的情況下,車輛的通行效率和換道次數都明顯下降,仿真結果與實際道路運行規律較相符。
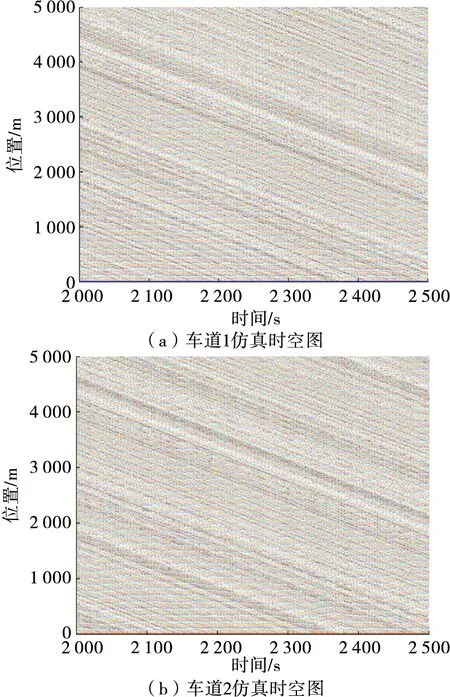
圖7 交通流密度為0.06 veh/m時雙車道時空圖
平均速度與交通流密度的關系見圖8。由圖8可知:速度-交通流密度關系曲線的趨勢與現實交通情況相符。交通流密度小于0.02 veh/m時,道路上的車輛行駛狀況很好,車輛可在本車道上以最大速度行駛,不需要通過換道就可獲得更好的速度,故車輛的平均速度無明顯變化。密度為0.02~0.08 veh/m時,3條曲線存在明顯差別,此時交通流密度適中,道路中具備一定換道條件,車輛會通過換道來獲得更優的行駛速度,故車輛會有較多的換道行為,導致兩車道平均速度存在差異,與仿真設置的雙車道模型行駛條件相符。密度大于0.1 veh/m時,3條曲線基本重合,平均速度與密度關系基本沒有變化。在交通流密度過大時,行駛在道路上的車輛沒有足夠的換道條件,大部分車輛不發生換道行為。
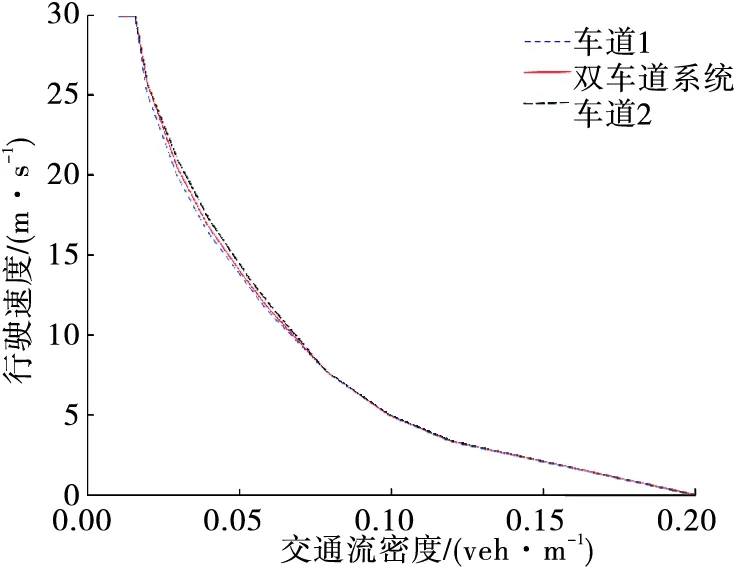
圖8 單條車道與系統整體的速度-密度關系
4 結語
將考慮多車信息的跟馳策略與換道策略相結合,建立雙車道連續元胞自動機模型,通過對模型進行模擬仿真,驗證模型的適用性和合理性,并探究交通流特性。通過仿真對比不同交通流密度下車輛時空變化,描繪不同密度下雙車道上車輛換道情況;通過分析對比雙車道的交通流三要素指標,證明所建雙車道連續元胞自動機模型與實際道路情況相符,能應用于實際交通流問題研究。

