基于高光譜數據的土壤全氮含量估測模型對比研究

殷彩云，白子金，羅德芳，彭 杰

（塔里木大學植物科學學院，新疆 阿拉爾 843300）

土壤全氮是衡量土壤肥力水平的重要指標之一，土壤氮含量指標被廣泛用于土壤養分供應能力、植物養分吸收和利用規律等農化分析中［1］，如何快速、準確和高效地監測土壤全氮含量，對作物生長和科學合理施用氮肥有重要意義。傳統測定土壤全氮含量的方法，不僅有耗時、耗力、成本高、環境污染等缺點［2-4］，而且在測定過程中一些化學試劑容易對人體造成危害，這種方法顯然不能滿足生產中大面積快速監測土壤全氮含量的需求。近年來，高光譜技術被廣泛用于土壤化學組分的測定，而基于光譜學原理的土壤氮素含量測定方法具有及時、省力、簡便、無污染等優點［5］，可為快速監測土壤全氮含量提供一個有效途徑。

隨著科學技術的進步，高光譜技術的發展為高效快速監測土壤養分提供了新的技術和方法。目前，國內外學者利用高光譜技術分析土壤全氮的相關研究已取得較大進展。Hummel等［6］研究發現土壤全氮含量與光譜反射率在可見光和近紅外波段相關性很高。Reeves等［7］利用近紅外光譜反射率特征波段建立的模型可對土壤全氮含量進行有效估測。Chang等［8］利用偏最小二乘法（PLSR）建立的基于光譜分析的模型可有效估測土壤全氮含量。前人的研究結果表明，利用土壤光譜反射率數據可進行土壤全氮含量估測，為后續的研究打下堅實基礎。盧艷麗等［9］利用可見光550和450 nm組成的光譜指數構建了土壤全氮含量預測模型，預測集R2達到了0.82以上。彭杰等［10］以895、1079、1138 nm等8個敏感波段反射率對數倒數的一階微分建立的多元逐步回歸模型R2達到了0.83。李焱等［11］通過提取特征波段，以多元逐步線性回歸和偏最小二乘回歸建模，發現反射率經二階微分變換后，以偏最小二乘回歸建模R2達到了0.96。王一丁等［12］對光譜反射率進行倒數對數和正交信號校正變換后，以PLSR建立的土壤全氮估測模型R2為0.92。近年來，國內一些研究多以高光譜數據結合非線性建模方法建立土壤養分含量估測模型，由于土壤光譜反射率和土壤養分含量之間是一種非線性關系，因此用非線性模型來估測土壤養分含量效果更好。如王世東等［13］、高小紅等［14］、張娟娟等［15］利用PLSR和BPNN兩種建模方法與光譜反射率及其數學變換建立土壤全氮估測模型，均具有較好的預測能力。鄭立華等［16］提取貢獻率超過99.98%的主成分建立BP神經網絡全氮含量模型，預測R2達到了0.81。以上研究表明，基于高光譜數據建立的模型是可以對土壤全氮含量進行估測的，但由于土壤類型和地區性差異，在實際工作中很難找到一種通用的模型來估測土壤全氮含量。

隨機森林（RF）是一種較新的數據挖掘模型［17］，具有運算速度快、穩定性高、數據適應能力強、在處理大數據集時預測精度高且不易產生過擬合等優勢［18-19］。馬利芳等［20］利用RF法構建了土壤鹽分主要離子估測模型。張智韜等［21］基于微分變換構建的SVMDA-RF模型預測了土壤有機質含量。目前RF多用于土壤有機質和土壤重金屬等估測，而用于土壤全氮含量的估測研究較少。因此，本研究利用新疆南疆5縣土壤樣品的高光譜和全氮含量數據，運用偏最小二乘回歸（PLSR）、支持向量機回歸（SVM）和隨機森林回歸（RF）3種方法，結合光譜反射率（R）及一階微分（FD）、倒數（1/R）、對數（lgR）和連續統去除（CR）變換數據分別建立研究區全區和分區土壤全氮含量估測模型。通過分析比較不同建模方法和不同數據變換后的估測模型精度，挑選出最優全氮含量估測模型，為研究區大范圍快速準確獲取土壤全氮含量提供技術支撐。

1 材料與方法

1.1 研究區概況

阿克蘇地區位于新疆維吾爾自治區中部，天山山脈南麓，塔里木盆地北部，其地理坐標為78°03′～84°07′E、39°30′～42°41′N，屬于暖溫帶大陸性氣候，年降水量42.4～94.4 mm，但年蒸發量高達1200～1500 mm［22］，年均氣溫9.9～11.5℃，光熱資源豐富，晝夜溫差大［23］。和田地區位于新疆維吾爾自治區最南端，南連昆侖山，東部與巴音郭楞蒙古自治州毗鄰，北部與阿克蘇地區相鄰，西部連喀什地區，地理位置為77°31′～84°55′E、34°22′～39°38′N，年均降水量35 mm，年均蒸發量2480 mm，屬于暖溫帶極端干旱荒漠氣候［22］。本研究選取的溫宿縣、拜城縣、和田縣、新和縣和阿瓦提縣隸屬于阿克蘇及和田地區。研究區種植作物以棉花、水稻、紅棗、蘋果、香梨、核桃為主，土壤類型主要以壤土和砂壤土為主，其保肥保水能力較差，土壤氮素含量普遍偏低，且該地區鹽漬化程度較高，嚴重影響作物的正常生長發育，對農業經濟收入造成了一定的制約。

1.2 土樣采集與處理

本研究土壤樣品采集地點（圖1）和采集數量分別為溫宿縣105個、拜城縣78個、阿瓦提縣60個、新和縣47個以及和田縣107個，共采集397個土壤樣品。為保證土壤樣品采集的精準性，用網格布點法采集土樣，各采樣點間距約為100 m，采樣深度為0～20 cm，每個土樣采集重量為500 g左右。土樣帶回室內后，去除雜草、礫石及動植物殘骸等雜質，在室內自然風干。風干后的土樣經研磨混勻后分成兩份，一份過2 mm篩，用于光譜數據的測定，一份過0.25 mm篩，用于土壤全氮含量的測定。

圖1 樣區分布圖

1.3 樣品分析

采用半微量開氏法測定土壤全氮含量，每個土樣設3次重復，重復間相對誤差控制在5%以內，取3次測量結果的平均值為最終測定值。各地區土壤全氮含量描述性統計見表1，由表1可知，全氮含量最大值出現在溫宿縣，為1.89 g/kg，最小值出現在新和縣，僅為0.07 g/kg，總體平均值為0.62 g/kg，各地區變異系數為10%～60%，根據雷志棟等［24］對變異系數的等級劃分，該研究區的土壤全氮含量屬于中等變異，有利于模型的構建。

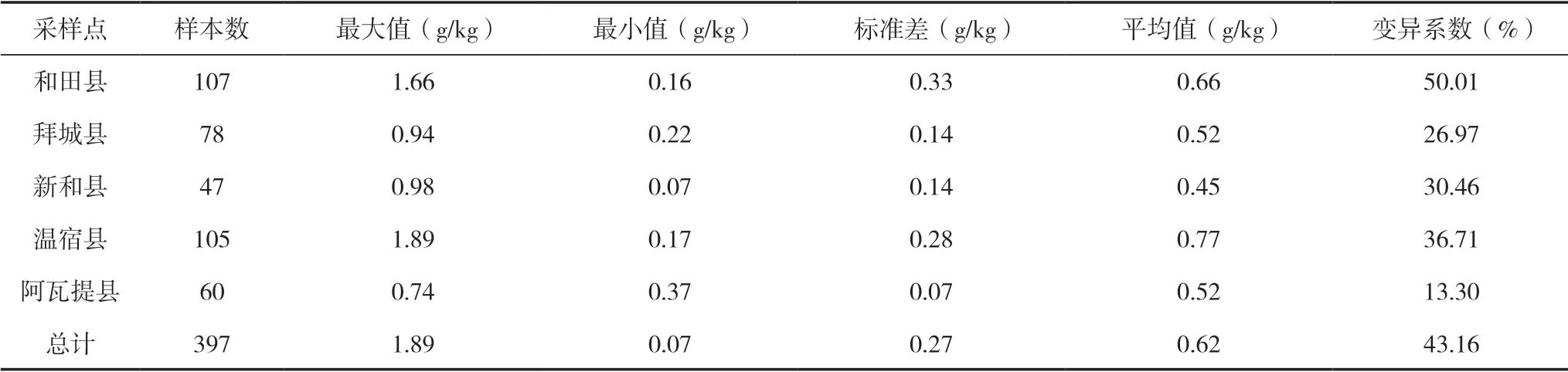
表1 各地區土壤全氮含量描述性統計

1.4 光譜數據的測定

采用美國ASD公司的FieldSpec Pro FR型光譜儀進行土樣光譜數據的測定，其測定波長范圍為350～2500 nm，光譜分辨率在350～1000 nm為3 nm，在1000～2500 nm為10 nm，數據重采樣間隔為1 nm［25］。測定土樣光譜前利用標準白板和黑板對光譜儀進行校準和調整。采集光譜時，為了減少外界環境對測定結果的影響，將土樣放置于直徑10 cm、深1.5 cm的內部涂黑的培養皿中，以50 W鹵素燈為測定光源，距離土樣表面70 cm，天頂角為30°，傳感器探頭位于土樣表面垂直上方15 cm處，采用25°視場角探頭，每測定一個土樣光譜進行白板校正，每個土樣采集10條光譜曲線，算數平均后得到該土樣的實際反射率光譜數據［26］。

1.5 光譜數據預處理

由于光譜曲線的350～399和2401～2500 nm波段受外界噪聲影響較大，故將其去除［13］，僅選取400～2400 nm波段進行光譜分析。為消除樣品間散射導致的基線偏移和減少平滑對有用信息的影響，本文采用了多元散射校正（multiplicative scatter correction，MSC）和Savitzky-Golay7點平滑對原始光譜反射率數據進行預處理，得到的反射率（R），并結合一階微分（first derivative，FD）、連續統去除（continuum removal，CR）、倒數（1/R）和對數（lgR）對反射率（R）進行數學變換。

1.6 建模方法及模型評價指標

建模思路為分區建模和全區建模，以所有采樣點獲得的數據進行全區建模，以各縣采集的數據（共5個縣）進行分區建模。為保證模型建立和驗證的合理性，所有模型的建模集和預測集都以全氮含量由低到高進行排序進行等間距抽樣，以2∶1劃分成建模集與預測集。建模方法選用偏最小二乘回歸（partial least squares regression，PLSR）、支持向量機回歸（support vector machines，SVM）和隨機森林回歸（random forest，RF）3種方法。PLSR和SVM建模和驗證在The Unscrambler X 10.5中完成，RF建模和驗證在R語言中完成。

模型評價指標選用決定系數（determination coefficient，R2）、均 方 根 誤 差（root mean square error，RMSE）和相對分析誤差（relative percent deviation，RPD）。其中，R2表示預測值與實測值之間的擬合程度，R2越大，說明預測值與真實值越接近，模型精度越好；RMSE表示預測值偏離真實值的程度，對于同一組數據，RMSE越小，說明預測值越接近真實值；RPD表示模型預測能力的強弱，根據Chang等［4］對RPD的等級劃分，當預測模型的RPD≥2時，表示該模型有較好的估測能力；當1.4≤RPD＜2.0時，表示該模型可以對樣品含量進行粗略估測；當RPD＜1.4時，表示該模型預測能力很差，無法對樣品含量進行估測。

2 結果與分析

2.1 不同全氮含量土壤反射率光譜特征

根據土樣將全氮含量分為4個等級，分別為等級1（＜0.5 g/kg）、等級2（0.5≤TN＜1.0 g/kg）、等級3（1.0≤TN＜1.5 g/kg）和 等 級4（≥1.5 g/kg）。圖2為根據每個等級的平均反射率得到4條反射率光譜曲線，由圖2可知，不同全氮含量土樣光譜曲線的變化規律基本一致，反射率變化范圍為0.15～0.50，在全波段范圍內，土壤全氮的光譜曲線變化整體呈緩慢上升趨勢，在1415、1920、2220 nm波段處有明顯的吸收特征。在可見光400～780 nm波段，光譜曲線較陡峭，反射率增長速度較快；在780～1900 nm波段，光譜曲線較平緩，反射率增長速度較慢；在1900～2100 nm波段，土壤光譜反射率隨波長的增加而增大，在2100 nm左右波段，反射率值達到最大值；在580～2400 nm波段土壤反射率也是隨著土壤全氮含量的增加而增大，但在400～580 nm波段并未呈現這樣的規律，出現了交叉現象。

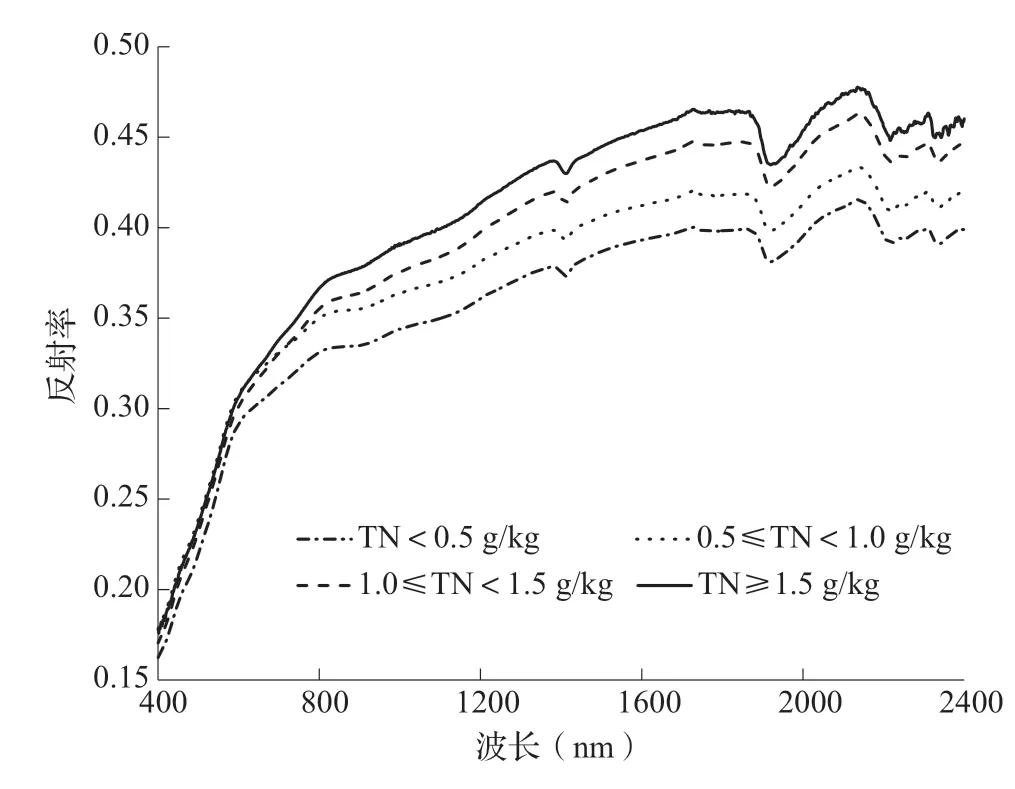
圖2 不同全氮含量土壤光譜反射率

2.2 土壤全氮含量與高光譜數據的相關性分析

將土壤R經FD、CR、1/R和lgR變換后，分別與土壤全氮含量做相關性分析，相關系數曲線如圖3。由圖3可知，土壤全氮含量與R在部分波段達到了較好的相關性；數據經FD變換后，在近紅外波段達到顯著性水平的波段數明顯減少，但有極少波段相關性有所提高，而大部分波段相對于R的相關性并未得到改善，反而有所下降；數據經CR變換后，在全波段內，土壤全氮含量和反射率數據相關性達到顯著性的波段數有明顯增加，且大多數波段相關性達到了極顯著水平，最大相關系數達到了0.43，是一種較好的光譜變換形式；數據經1/R和lgR變換后，lgR變換后的相關性曲線和反射率R相關系數曲線走勢基本相同，差異較小，1/R變換后的相關系數曲線與R相關系數曲線相對稱，三者達到顯著性水平以上的波段數基本相同。

圖3 全氮含量與高光譜數據的相關分析

2.3 土壤全氮含量估測模型的建立與檢驗

為了得到土壤全氮含量最優估測模型，本文針對性地使用反射率及其4種數學變換后數據，利用PLSR、SVM和RF對5個地區土壤全氮含量進行建模，各模型結果見表2。由表2可知，3種方法建立的模型效果各不相同，在進行分區建模時，PLSR最優模型建模集的R2為0.83，RMSE為0.14 g/kg，預測集R2為0.73，RMSE為0.17 g/kg，RPD為1.82，未達到2.0以上，說明PLSR模型效果一般，只能對樣品全氮含量進行粗略估測；SVM最優模型建模集R2為0.78，RMSE為0.16 g/kg，預測集R2為0.75，RMSE為0.16 g/kg，RPD為1.97，也未達到2.0以上，說明SVM模型也只能對樣品全氮含量進行粗略估測。SVM較PLSR模型，建模集的R2雖然下降了0.05，但預測集的R2上升了0.02，RMSE下降了0.01 g/kg，RPD上升了0.15，說明SVM模型的預測能力略高于PLSR模型。而RF最優模型建模集的R2為0.87，RMSE為0.08 g/kg，預測 集R2為0.86，RMSE為0.08 g/kg，RPD達 到 了3.52，說明RF模型預測能力較好，可以對樣品全氮含量進行精確估測。

全區模型與分區模型相比，PLSR、SVM和RF進行全區建模時，建立的最優模型RPD分別為1.50、1.62和3.24，均低于分區最優模型，但PLSR和SVM模型的RPD均大于1.40，可以對樣本全氮含量進行粗略估測；而分區建模部分地區建立的PLSR和SVM模型不能用于全氮含量估測，說明全區模型的穩定性要高于分區模型。3種模型相比較，RF模型建模集R2為0.80～0.87，預測集R2為0.76～0.85，RPD為2.35～3.52，RF估測全氮含量的結果較穩定，整體估測精度較高，是一種較好的建模模型。

由表2分析可知，不同數據變換后，模型的精度也有所變化，在5個不同地區，由于土壤類型和采樣數量的不同，各種數據變換后建模精度無明顯變化規律。PLSR、SVM和RF最優模型分別是在光譜R數據經CR、1/R和lgR變換后建立的。在5個地區建立的最優模型均是RF模型，在和田縣、阿瓦提縣和新和縣，數據經lgR變換后，建立的模型精度最高，而在拜城縣和溫宿縣，數據分別經1/R和CR變換后，建立的模型精度最高。其中阿瓦提縣和新和縣以PLSR和SVM建立的模型精度明顯低于其他地區，可能是由于這兩地區采樣點位置比較集中，采樣數較少，土壤類型單一，總體缺乏代表性，構建的模型效果較差。

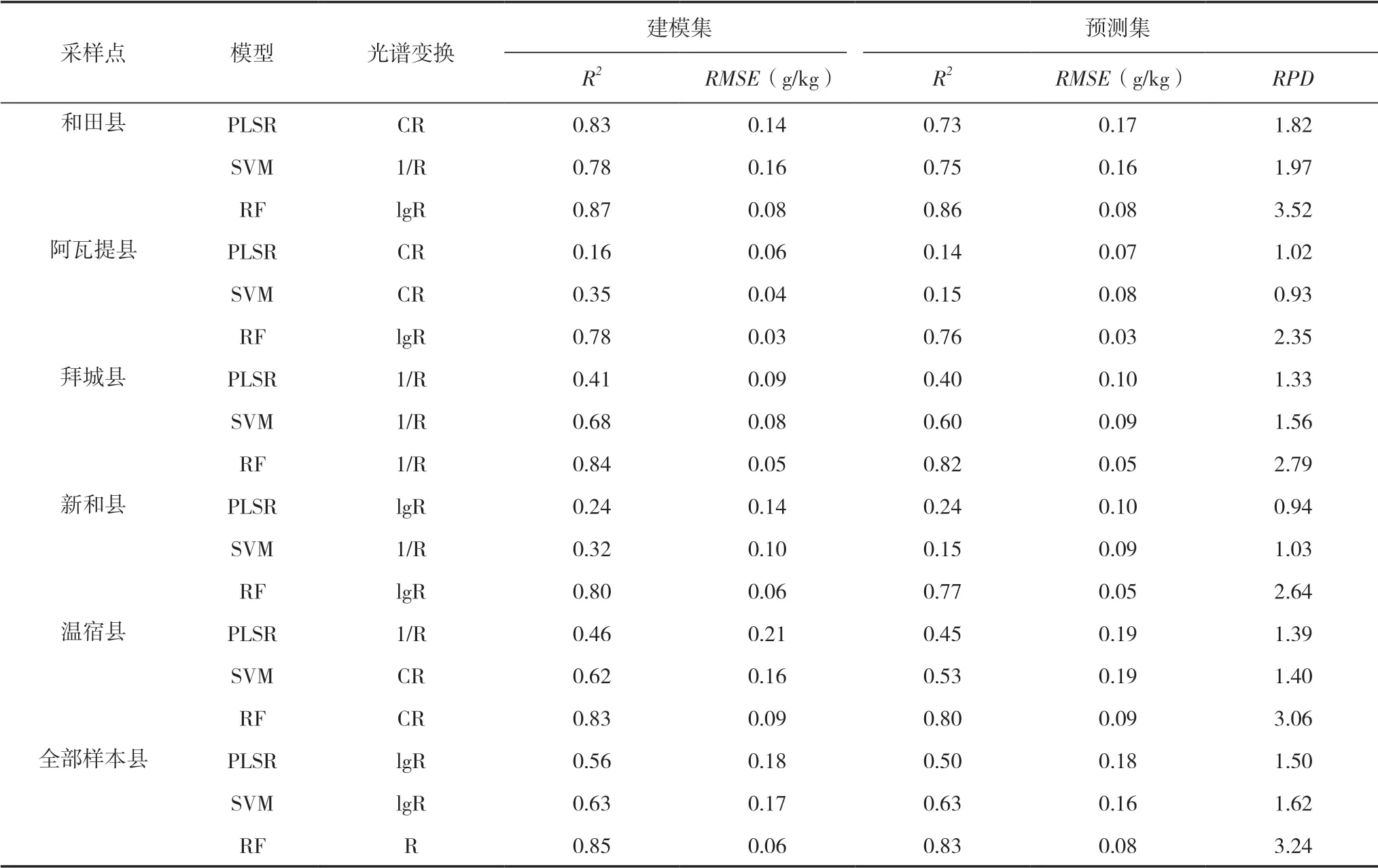
表2 土壤全氮含量估測最優模型

3 討論

3.1 光譜預處理對建模精度的影響

建模時將光譜R進行預處理可消除土壤類型（質地、顆粒大小等）及所處環境（溫度、濕度等）對建模效果的影響，并適當提高模型的預測能力［27-28］。徐永明等［29］運用一階導數（FDR）、倒數（1/R）、倒數對數［lg（1/R）］、波段深度4種數學變換后的光譜R與總氮含量進行分析，發現FDR和lg（1/R）變換后的回歸和驗證精度較高。陳紅艷等［30］利用遺傳算法結合偏最小二乘法對光譜的5種數據變換分別建模，發現反射率的一階導數表現最佳。Zornoza等［31］將光譜數據進行多元散射校正和一階微分處理后，建立的模型精度有明顯提高。本研究結果與上述研究結果基本一致，本文利用R及FD、1/R、lgR和CR 4種變換后的光譜R數據進行建模，FD變換后模型的精度較低，可能原因是一階微分在放大光譜特征波段的同時會放大噪聲和無關因素的干擾，這在一定程度上也會降低建模精度，而其他數據變換在建模中對建模精度都有不同程度的提高，更能反映出土壤全氮含量的變化特征。

3.2 不同建模方法比較

土壤養分含量的高光譜估測模型主要有線性模型和非線性模型，合理選擇建模方法是提高反演精度和效率的重要步驟。PLSR方法借鑒了主成分分析、典型相關分析和普通多元線性回歸3種分析方法的優點［32］，較好地解決了樣本數少于變量數等問題。王海江等［33］研究了基于特征波段建立的PLSR、SVM和SMLR模型，發現PLSR模型精度最高。劉秀英等［34］運用相關分析和偏最小二乘回歸建立的黃綿土土壤全氮預測模型可對0～40 cm土壤全氮進行有效預測。而在本研究中，PLSR模型的精度卻為最低，這可能是研究地域和土壤類型差異較大，總體缺乏代表性，土壤光譜存在較大的差異性，而且PLSR屬于線性回歸模型，而全氮含量跟光譜反射率是一種非線性關系，因此無法對全氮含量的非線性特征進行表征，從而難以保證估算結果的精確性和可靠性。代希君［35］利用ENVI 5.1將高光譜數據轉換為多光譜數據，采用PLSR和SVM建立土壤鹽分反演模型，結果發現SVM模型反演精度優于PLSR模型。劉煥軍等［36］利用RF構建的基于影像波段和光譜指數的土壤有機質含量預測模型精度R2為0.69。王金鳳等［37］運用RF、SVM、PLSR 3種方法進行元素含量與光譜變量建模后，發現基于二階微分變換的RF準確度最高。為進一步提高模型精度，鑒于以上研究結果，本研究采取了非線性建模方法SVM和RF建立全氮含量估測模型，發現SVM建模精度較PLSR有小幅度的提高，而RF較PLSR建模精度有大幅度的提高，由于RF具有穩定性高、數據適應能力強、抗噪聲能力強、在處理大數據集時預測精度高且不易產生過擬合等優點［18-19］，因此利用RF模型可有效提高模型預測精度和穩定性。

4 結論

根據不同等級土壤全氮含量光譜曲線得出，各曲線走勢基本一致，在近紅外波段的1415、1920、2220 nm處有明顯的吸收特征。對比反射率曲線得出，在580～2400 nm內R隨土壤全氮含量的增加而增大。

對土壤光譜R進行一定的數學變換，可提高土壤全氮和土壤光譜R的相關性，本研究選取的連續統去除變換明顯提高了光譜與土壤全氮的相關性，相關系數最大，達到了0.43，更能反映土壤全氮含量變化特征。

RF模型在預測土壤全氮含量的過程中具有較高的估測精度，其整體預測精度要高于PLSR和SVM模型，可以對土壤全氮含量進行精確估測；SVM模型的估測精度雖然高于PLSR模型，但SVM和PLSR模型只能對土壤全氮含量進行粗略估測。對光譜數據進行數學變換后建模，除一階微分變換外，其他數據變換均對模型精度有不同程度的提高。RF模型無論是分區建模還是全區建模，模型在各種數據變換之后預測精度差異性較小、模型結果均勻、穩定性高、適用性好。分區最優模型的精度要高于全區最優模型，但分區模型差異性明顯，而全區模型綜合了各地區土壤類型的差異，模型的穩定性較高，在進行分區建模時可通過增加樣本數來提高模型的精確性和穩定性。