美英早期代數教科書中的等比數列知識

韓粟 汪曉勤

摘? 要：對1800—1959年間出版的118種美英代數教科書進行研究，研究發現：在等比數列這個主題上，早期代數教科書共采用了3種引入方式、4種定義和8種求和公式推導方法. 這些方式或方法為如今的等比數列教學提供了豐富的素材和有益的思想養料.

關鍵詞：等比數列;引入方式;定義;求和公式

一、引言

從兩河流域神秘的楔形文字到恒河流域深奧的吠陀梵文，從埃及大陸《萊茵德紙草書》記載的財產之和到齊魯大地上惠子與墨子的尺棰取半之爭，等比數列的悠久歷史從古代四大文明中可見一斑. 隨著數學的發展，等比數列的概念不斷完善，知識不斷豐富，成為刻畫現實世界的一類函數模型.

等比數列是如今高中數學中的重要內容，迄今已有不少教師嘗試從HPM的視角進行教學設計并付諸實踐. 受歷史素材的局限，已有的課例在等比數列概念教學中采用了少數歷史上的問題，如古印度的貓鼠問題和斐波那契的棋盤問題，以揭示知識的必要性;在求和公式的教學中采用了歷史上的若干推導方法，包括源于古埃及的遞推法或方程法、歐幾里得的比例法，以及歐拉的錯位相減法，以呈現方法的多元性. 但是，教師并未考慮等比數列概念形成的自然性、定義的多元性，以及更多推導求和公式的方法.

歷史上的數學教科書是一座寶藏，其中蘊含了豐富的教學資源、有益的思想養料，以及獨特的知識呈現方式. 為此，我們聚焦等比數列的相關內容，對19世紀初期至20世紀中期出版的美國與英國代數教科書進行研究，嘗試回答以下問題：早期教科書如何引入并定義等比數列？教科書中有哪些推導求和公式的方法？對如今的教學有何啟示？

二、教科書的選取

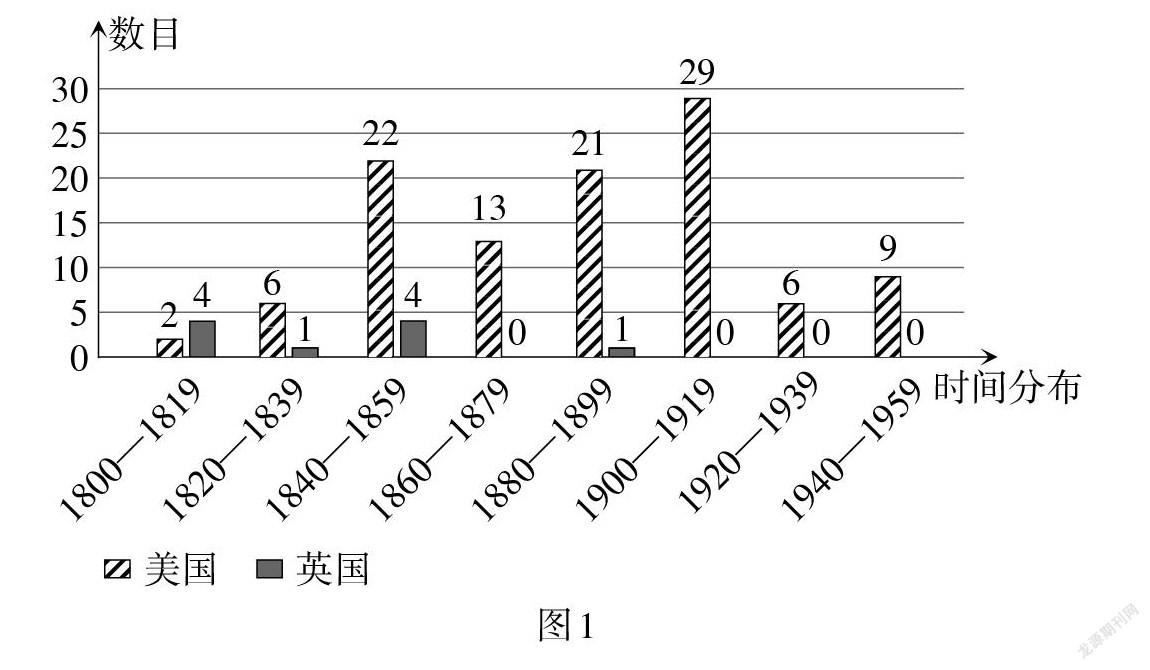
選取1800—1959年出版的118種美英早期代數教科書為研究對象，其中108種為美國出版，10種為英國出版，并將每20年劃分為一個時間段，出版時間分布如圖1所示. 對于同一作者且內容無明顯差異的教科書，視為同一種，并選擇出版時間最早的版本.

早期教科書中等比數列的知識不勝枚舉，本文擬對引入、定義及求和公式三個知識點進行深入研究. 由于本文面向中學數學教學，故不再嚴格區分數列與級數，統稱數列.

在研究的118種教科書中，等比數列內容主要分布于“比例”“數列”“幾何比例”“幾何數列”“數列與對數”“冪與指數函數”“數學歸納法”等章節.

三、等比數列的引入

經過統計和分析，118種教科書中等比數列內容的引入方式可以分成直接引入、比例引入、數列引入、指數引入四類，其分布情況如圖2所示.

1. 比例引入

在被研究的118種教科書中，有19種教科書采用幾何比例引入等比數列的方式. Lawrence（1853）先定義幾何比是一個量除以另一個量的商，再定義幾何比例是兩個相等的幾何比，最后通過推廣相等幾何比的個數引入等比數列.

2. 數列引入

在被研究的118種教科書中，有48種教科書以數列為屬概念，引入作為種概念的等比數列. 包含兩種情形. 一種是通過數列分類的方式引入，如Clarke（1881）指出，數列可以按有窮與無窮、遞增與遞減、收斂與發散分類，還可以按數列內部特定規律來分類，以此引入等比數列. 另一種是通過具體數列來引入，如Milne（1881）先給出以下數列：（1）[2x，4x，8x，16x;]（2）從2a開始，依次乘以3a所得到的5項數列;（3）從a開始，依次乘以r所得到的6項數列.

3. 指數引入

在被研究的118種教科書中，有3種教科書采用了指數引入的方式. 其中，Mitchel（1845）利用了指數方程：到目前為止，我們都在討論那些不把未知量作為指數的方程. 而考試中有兩類主題都出現了一種方程[ax=b，] 其中[a]和[b]是已知量，[a]的指數[x]是未知量，這兩類主題就是等比數列和對數. Smail（1931）則利用了指數型函數：首先取函數[y=32x，] 依次計算[x=0，1，2，3，…]時[y]的值，得到一組數字[3，6，12，][24，…，] 這組公比為2的數是等比數列的一個例子. 一般地，取指數型函數[y=kax，] 計算[x=0，1，2，3，…]時對應的[y]值，得到一組數字[k，ka，ka2，ka3，…，] 這組公比為[a]的數是等比數列.

4. 引入方式的演變

圖3給出了118種教科書中等比數列內容引入方式的時間分布情況. 由圖3可見，19世紀最早的教科書均采用比例引入方式，“比例”一章的主要內容通常為比與比例性質的討論，等比數列所占篇幅極少. 19世紀中期，教科書中數列知識開始單獨成章，自數列引入方式出現后，比例引入方式逐漸退出歷史舞臺. 與直接引入相比，數列引入方式通過演繹或歸納獲得等比規律，為等比數列概念的出現奠定了基礎. 因此，進入20世紀，直接引入方式的使用頻率明顯下降，數列引入成為主流.

指數概念與符號產生于17世紀，用指數引入等比數列與歷史序恰好相反，在我們所研究的早期教科書中，兩種采用指數引入方式的教科書均出版于20世紀20年代后，此時函數在數學課程中的地位逐漸提升，將數列視為特殊的函數，符合數列知識的邏輯序.

四、等比數列的定義

根據等比數列的不同構造方式，早期教科書中的等比數列定義可以分為幾何比例定義、比值定義、乘法定義和除法定義四種，其分布情況如圖4所示.

[圖4] [81][乘法定義][比值定義][19][除法定義][13][幾何比例定義][5]

1. 幾何比例定義

在被研究的118種教科書中，有5種教科書采用了幾何比例定義. Simpson（1800）以“4個數構成算術或幾何比”的定義為基礎，進一步定義“當每兩個相鄰項的差或比值相等時，則稱它們構成連續比. 例如，[2，4，6，8，…]為連續算術比例，[2，4，8，16，…]構成連續幾何比例，這類比例又稱為數列，它們始終滿足同一規律.

2. 比值定義

在被研究的118種教科書中，有19種教科書采用了比值定義. Hall（1840）用符號語言表述：如果有一個數列[a1，a2，a3，…]的任一項與前一項的比值在整個數列范圍內都相同，即[a2a1=a3a2=a4a3=…， ]則稱數列[a1，a2，a3，…]為等比數列. 比值定義揭示了“等比數列”一詞的術語之本.

3. 乘法定義

在被研究的118種教科書中，有81種教科書采用了乘法定義，是早期教科書中出現頻率最高的定義方式. 該定義的雛形可以上溯到古埃及人的倍乘法. 不同教科書的表述不盡相同，定義中對于乘數的描述集中在常量、常倍數和公因子三種，具體見下表.

Lilley（1892）認為，正如等差數列由重復的加法或減法構成，等比數列也由重復的乘法構成. 這說明初等數學中也蘊涵著研究代數運算結構的思想.

4. 除法定義

在被研究的118種教科書中，有13種教科書采用了除法定義，即一列數中，若任何一項（第一項之后）除以前一項的商在整個數列中都相同，則這個數列是等比數列. 歷史上曾短暫地出現過等商數列的命名，現行教科書以quotient（商）的首字母q作為公比的符號表示.

5. 定義的演變

圖5給出了等比數列定義的時間分布情況. 由圖5可知，5種幾何比例定義僅存在于19世紀60年代以前，而比值定義一直存在至20世紀中期. 幾何比例定義中“連續”一詞過于直觀，不符合數學的抽象性，而比值定義既保留了“比較”的知識源流，又突出了“比值”的定量描述，很好地滿足了數學的抽象性與嚴謹性.

乘法定義和除法定義都源于四則運算，但乘法定義中后一項為前一項與公比乘積的表述，或許更符合學生從前到后認識一列數的過程，順勢可以獲得等比數列的通項，所以較除法定義而言，乘法定義廣泛分布于西方早期乃至現行教科書.

五、求和公式的推導

記等比數列的首項為[a1，] 項數為n，末項（或通項）為[an，] 公比為q，前n項和為[Sn.] 118種教科書中出現了兩種形式的求和公式：[Sn=a1qn-a1q-1;Sn=anq-a1q-1.]

早期教科書中呈現了豐富的求和公式推導方法，可以分為錯位相減法、錯位相加法、乘子消項法、遞推累加法、掐頭去尾法、恒等式法、解析幾何法、數學歸納法共8類，各類方法的數目如圖6所示. 其中，3種教科書采用了兩種推導方法，1種教科書直接給出了公式.

1. 錯位相減法

在被研究的118種教科書中，有100種教科書采用了錯位相減法，是教科書中運用最廣泛的推導方法.

Peacock（1842）編寫的《代數論》中，首先將等比數列的前n項和表示為[Sn=a1+a1q+ … +a1qn-1，] 等式兩邊同時乘以公比[q，] 得[qSn=a1q+a1q2+ … +a1qn-1+a1qn.]

兩式相減，即得[Sn=a1qn-a1q-1.]

Peacock指出運用上述方法的原因：當我們將兩個數列逐項相減，則僅保留原數列的首項[a1]與新數列的末項[a1qn，] 而消去兩數列中其他相同的項. 部分教科書通過把[Sn=a1+a1q+ … +a1qn-1，qSn=a1q+a1q2+ … +][a1qn-1+a1qn]右端的相同項對齊來表示兩和式的錯位，更直觀地表示出消項的過程.

2. 錯位相加法

對錯位相減法稍加改變即得錯位相加法：在[Sn=a1+a1q+ … +a1qn-1]兩邊同時乘以公比的相反數[-q，]得[-qSn=-a1q-a1q2- … -a1qn-1-a1qn.] 兩式相加，即得[Sn=a1qn-a1q-1.]

在和式兩邊同乘q或[-q]的構造看似是從天而降，但其本質與初中解二元一次方程組的加減消元法并無二致，變化的只是消去和保留的項數，樸素的化簡思想始終如一.

3. 乘子消項法

上述兩種方法都需要構造一個新的和式，對兩式進行運算、消項. 若在[Sn=a1+a1q+ … +a1qn-1]兩邊同時乘以常數[q-1，] 則[q-1Sn=q-1a1+a1q+ … +a1qn-1.] 化簡，得[q-1Sn=][a1qn-a1，] 即得[Sn=a1qn-a1q-1.]

從乘法分配律的角度分析，等式兩端同時乘以[q-1，] 一邊構造亟待消去的下一項，一邊消去方才構造的上一項，循環往復，最后只剩下[a1]和[a1qn]兩項，動態的消項過程隱含在單個和式里，這種一步到位的方法對學生的代數思維提出了更高要求.

4. 遞推累加法

在被研究的118種教科書中，有7種教科書采用了先由定義遞推，后由累加化簡的方法推導等比數列的前n項和公式.

由等比公式定義，得[a2=a1q，a3=a2q，a4=a3q，a5=][a4q，…，an=an-1q.] 所有等式相加，得[a2+a3+a4+a5+ … +]

[an=a1+a2+a3+a4+ … +an-1q.] 等式左邊的[n-1]項和等于[Sn-a1，] 等式右邊括號中的[n-1]項和等于[Sn-an，] 即[Sn-a1=Sn-anq.] 合并同類項，得[Sn=][anq-a1q-1.]

5. 掐頭去尾法

Harney（1840）以[n=5]為例，借助等比數列通項公式，記前5項和[S5=a1+a1q+a1q2+a1q3+a1q4.] 將等式左端“掐”去頭部，得[S5-a1=a1q+a1q2+a1q3+a1q4;] “去”掉尾部，得[S5-a1q4=a1+a1q+a1q2+a1q3.] 比較兩式，得[S5-a1=S5-a1q4q.] 合并同類項，化簡得[S5=][a1q5-a1q-1.] 因為上式中[a1q5 ]是第5項[a1q4]與公比[q]的乘積，所以用[a1qn-1]代替[S5]中的第5項，即得等比數列前[n]項和[Sn=a1qn-a1q-1.]

6. 恒等式法

在被研究的118種教科書中，有8種教科書借用多項式除法中的一個恒等式推導得到求和公式. 最早，Ryan（1826）用錯位相減法推導公式時意識到當[q=1]時，公式[Sn=a1qn-a1q-1]中[Sn=a-a1-1=00，] 他以恒等式[1-qn1-q=qn-1+qn-2+qn-3+ … +q+1]給出解釋，在這種特殊情況下，符號[00]的值應該與[na1]相等，意圖說明公式[Sn=a1qn-a1q-1]的普適性.

Taylor（1843）在“多項式除法”一章中由[xn-ynx-y=][xn-1+xn-2y+xn-3y2+ … +xyn-2+yn-1]對[x]取特殊值[1]，用[q]替換[y]得到恒等式[1-qn1-q=qn-1+qn-2+qn-3+ … +q+1，]而等比數列和式可以寫成[Sn=a11+q+q2+ … +qn-1.]括號中的多項式與上述恒等式右邊相同，將上述恒等式代入，即得[Sn=a1qn-a1q-1.]

這一方法指出，等比數列求和的關鍵不在于首項，而在于公比. 求解任意等比數列的前n項和，化歸后都是求解首項為1、公比相同的等比數列前n項和.

7. 解析幾何法

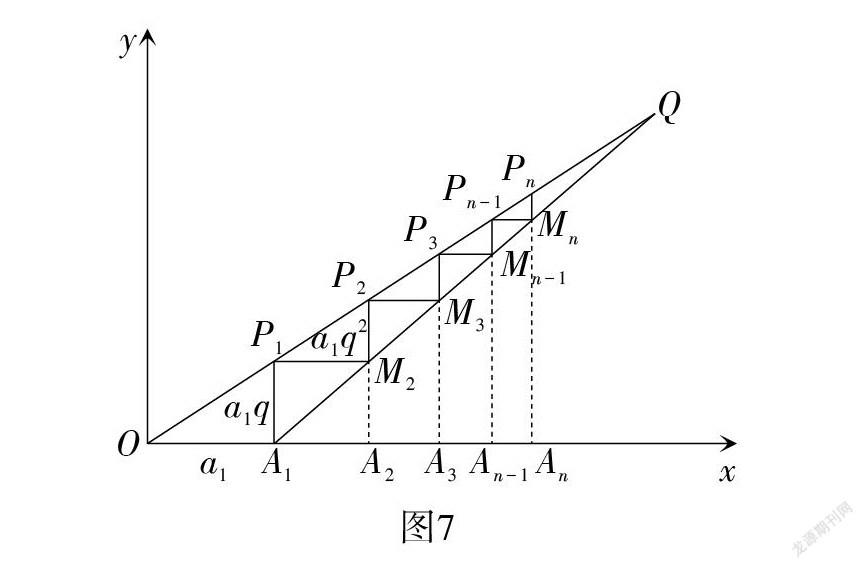
Smail（1931）在平面直角坐標系中巧妙構造出等比數列的圖象，以[a1>0，0<q<1]為例，先畫出直線[OQ：][y=qx，] 并確定[x]軸上一點[A1a1，0，] 過點[A1]作[y]軸的平行線，交直線[OQ]于點[P1，] 則[A1P1=a1q.] 再過點[P1]作平行于[x]軸，長度等于[a1q]的線段[P1M2]……不斷重復上述步驟，可以得到點列[Pn， Mn]和[An，] 顯然點[An]的坐標為[Sn，0.]

如圖7，因為直線OQ的斜率為q，所以[PnAnOAn=q.] 因為[PnAn]=[Sn+1-a1，] 所以[Sn+1-a1Sn=q.] 將[Sn+1=Sn+a1qn]代入，移項化簡，得[Sn=a1qn-a1q-1]. 其他情形同理可得.

[y][x][圖7]

8. 數學歸納法

數學歸納法并非編寫者在推導求和公式時的首選，他們往往將“數學歸納法”一章置于“數列”一章之后，將證明求和公式留作數學歸納法的應用. 假設等比數列前[n]項和公式[a1+a1q+a1q2+ … +a1qn-1=a1-a1qn1-q]成立，在等式兩邊同時加[a1qn，] 得[a1+a1q+a1q2+ … +][a1qn=a1-a1qn1-q+a1qn=a1-a1qn+a1qn-a1qn+11-q=a1-a1qn+11-q.]因為上式對[n=1]同樣成立，所以對所有正整數n都成立. 雖然在今天看來這并不是嚴格的數學歸納法，但是其符合早期教科書中先歸納假設、再驗證特例的順序.

9. 推導方法的演變

除去數學歸納法，其他方法都是設法消去求和式的[n-2]個項，建立只含3個基本量的求和公式. 如圖8，早期教科書中等比數列求和公式的推導方法從多元逐漸走向單一，錯位相減法在各時期內被使用頻率最高，其余方法在教科書中交替出現，到20世紀中期，錯位相減法成為教科書中唯一呈現的方法.

[1800—1819][時間分布][1820—1839][1840—1859][1860—1879][1880—1899][1900—1919][1920—1939][1940—1959][求和公式推導方法占比][0][90%] [100%][80%][70%][60%][50%][40%][30%][20%][10%] [錯位相減法] [錯位相加法] [乘子消項法] [遞推累加法] [掐頭去尾法] [恒等式法] [數學歸納法] [解析幾何法] [圖8]

19世紀早期遞推累加法的頻繁運用得益于此時期教科書對數列遞推關系的重視，隨后這種方法不再出現. 掐頭去尾法、錯位相加法、乘子消項法都與錯位相減法一脈同源，其中掐頭去尾法用移項代替相減，錯位相加法以公比的相反數為乘子從而變相減為相加，乘子消項法以公比與1的差作為乘子，內蘊了錯位相減的過程. 解析幾何法的誕生可謂“無心插柳”. 同樣，恒等式法一開始也錯誤地用于統一[q≠1]和[q=1]兩種情形下的求和公式，20世紀早期才作為少數教科書中的第二種方法出現.

關于[q=1]的迷思，直到Wilczynski（1916）的《大學代數及應用》一書出版才得以破解，他指出和式兩邊同時除以[1-q]時除數不能為0. 這么簡單的一個問題卻難倒了一眾數學家，由此看出分類討論的數學思想不可或缺！

六、結論與啟示

以上我們看到，在等比數列這一主題上，美英早期教科書采用了豐富的引入和定義方式，以及前n項和公式的推導方法，這些方式或方法為如今的教學帶來了諸多啟示.

其一，在引入并定義等比數列時，可以讓學生先描述給定數列逐項之間的規律，根據歷史相似性，乘法定義或除法定義都可能成為學生在概念形成過程中的語言表征. 通過展示“比—比例—等比數列”的知識脈絡，引導學生體會教科書采用比值定義的合理性，構建知識之諧.

其二，在推導等比數列求和公式時，傳統的錯位相減法可能讓學生產生“為什么在和式兩邊同乘公比”的疑問，教師可以引導學生變換和式兩邊的乘數，探究得到錯位相加法和乘子消項法，深刻認識到同乘的目的是消去中間項，而乘數的選擇也不限于公比. 此外，用移項代替相減可以導出掐頭去尾法. 根據前后項的遞推關系不僅可以導出代數上的遞推累加法，還可以在坐標系中構造圖象，由斜率為公比導出幾何法，彰顯方法之美.

其三，數學歸納法和恒等式法可以用來證明猜想、歸納得到的求和公式，體現數學的嚴謹性. 雖然學生尚未學習多項式除法，但乘除互為逆運算的關系啟示著可以通過多項式乘法來獲得所需恒等式，并用綜合法證明求和公式，培養邏輯推理素養，實現能力之助.

其四，數學史的融入可以揭示等比數列的知識源流. 例如，借助微視頻技術，展現西方早期教科書中等比數列定義及求和方法的演變，通過古今對照和中西對比，體現數學文化的多元性，展示文化之魅. 數學家對科學真理的熱愛、追求和探索，有助于學生形成動態的數學觀，體會數學背后的理性精神，最終達成德育之效.

參考文獻：

[1]汪曉勤. HPM：數學史與數學教育[M]. 北京：科學出版社，2017.

[2]LAWRENCE C D. Elements of Algebra[M]. Auburn：Alden，Beardsley and Company，1853.

[3]CLARKE J B. Algebra for the Use of High Schools，Academies and Colleges[M]. San Francisco：A. L. Bancroft and Company，1881.

[4]MILNE W J. The Inductive Algebra[M]. New York：American Book Company，1881.

[5]MITCHEL O M. An Elementary Treatise on Algebra[M]. Cincinnati：E. Morgan and Company，1845.

[6]SMAIL L L. College Algebra[M]. New York：McGraw-Hill book company，1931.

[7]SIMPSON T. A Treatise of Algebra[M]. London：L. Hanford for F. Wingrave，1800.

[8]HALL T G. The Elements of Algebra[M]. London：John W. Parker，1840.

[9]CURTIS L J. Concept of the Exponential Law Prior to 1900[J]. American Journal of Physics，1978，46（9）：896-906.

[10]BRADBURY W F. Eaton’s Elementary Algebra[M]. Boston：Thompson Bigelow and Brown，1868.

[11]CHASE S. A Treatise on Algebra[M]. New York：Appleton，1849.

[12]COLENSO J W. The Elements of Algebra[M]. London：Longman and Company，1849.

[13]LILLEY G. The Elements of Algebra[M]. Boston：Silver Burdett and Company，1892.

[14]PEACOCK G. A Treatise on Algebra[M]. Cambridge：J. and J. J. Deighton，1842.

[15]HARNEY J. H. An Algebra upon the Inductive Method of Instruction[M]. Louisville：Morton and Griswold，1840.

[16]RYAN J，ADRAIN R. An Elementary Treatise on Algebra[M]. New York：Collins and Hannay，1826.

[17]TAYLOR J M. A College Algebra[M]. Boston：Allyn and Bacon，1889.

[18]方倩，汪曉勤. 20世紀中葉以前西方代數教科書中的數學歸納法[J]. 數學教學，2017（11）：1-4，31.

[19]WILCZYNSKI E J，SLAUGHT H E. College Algebra[M]. Boston：Allyn and Bacon，1916.

1882501705269