長江經濟帶工業綠色發展效率測度
——基于考慮指標偏好的廣義DEA模型

陶碩 TAO Shuo

（重慶師范大學經濟與管理學院，重慶 401331）

0 引言

黨的十九大報告提出“加快生態文明體制改革，建設美麗中國”，強調人與自然是命運的共同體，制定優先重視保護的方針，并制定節約資源和保護環境的產業結構和生產方法。1999年，戴星翼[1]在《走向綠色的發展中》一書中首次明確提出“綠色發展”一詞，從整個社會經濟層面，討論經濟的可持續性發展（即綠色經濟發展）問題。

工業作為國民經濟支柱，工業綠色發展對于推動我國經濟高質量發展具有重大意義。近幾年來，不少學者開始對工業綠色發展效率進行了研究。在研究方法上，大多數學者采用數據包絡分析方法[2]（Data Envelopment Analysis,DEA），DEA方法是一種評價多投入多產出的決策單元相對效率的非參數方法，是一種相對客觀、科學的計算方法，是目前最常用的測度工業綠色發展效率的模型。吳旭曉[3]基于2005-2013年省級面板數據，運用超效率DEA視窗分析方法測算了青海、河南和福建的工業綠色效率。黃磊等人[4]采用考慮非期望產出的全局超效率SBM模型及泰爾指數分析2011-2016年長江經濟帶城市工業綠色發展效率的時空演變規律。王建民等人[5]基于長江經濟帶2007-2016年11省市面板數據，運用Super-SBM模型與Malmquist指數對工業綠色發展效率進行動靜分析。丁顯有等人[6]采用基于非期望產出的SBM-DDF模型測度了長三角城市群18個重要城市的綠色發展效率、創新發展效率。

傳統的DEA方法通常以相同的目標、任務、外部環境和投入產出指標來評價決策單元。評價的參考框架默認為有效DMUs，沒有提供獨立選擇評價標準的自由度。實際上，決策者可能需要根據需求選擇合適的參照集。參考框架不僅是有效的決策單元本身，而且是一般單位、較差單位或特定單位。比如，低效DMU中的決策者可能希望將DMU與一些他們能夠在短時間內匹配的適當樣本單元進行比較，而不是與高效DMU進行比較。因此，馬占新[7]開發了一組具有廣義參考集的DEA模型，稱作廣義DEA模型，讓決策者根據需求選擇合適的樣本單元。

考慮到在綠色發展效率評價中，決策者對某些評價指標有明顯的偏好，并且需要自主選擇評價參考系，因此，本文選擇指標偏好順序作為指標權重約束形式[8]，將決策者對指標權重偏好納入到廣義DEA模型中，構建了帶權重偏好的廣義DEA模型，將其應用于中國長江經濟帶工業綠色發展效率測度。

1 考慮指標偏好的廣義DEA模型

1.1 廣義DEA

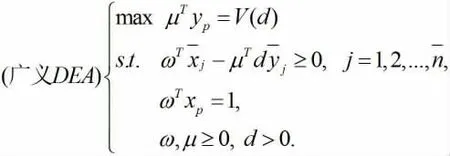
其中，xp=（x1p，x2p，…，xmp）T表示DMUp的投入指標向量，yp=（y1p，y2p，…，ysp）T表示DMUp的產出指標向量，=表示SUj的投入指標向量）T表示SUj的產出指標向量，ω=（ω1，ω2，…，ωm）T表示投入指標權重向量，μ=（μ1，μ2，…，μs）T表示產出指標權重向量，d是一個移動因子。

1.2 考慮指標偏好的廣義DEA模型

本節將權重偏好引入廣義DEA模型，構建了考慮指標偏好的廣義DEA模型（Generalized DEA with Indicator Preference，GDEA-IP）。假設有n個DMU和個樣本單位。DMU和樣本單元的特征可以用m種投入和s種產出來表示。對于GDEA-IP（d）模型表示如下：

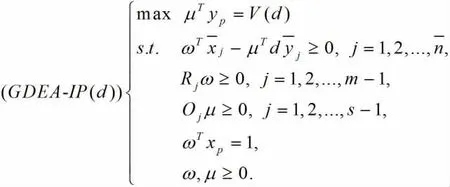
其中，R為投入的指標偏好矩陣，O為產出的指標偏好矩陣，Rj為R的第j行，Oj為O的第j行。GDEA-IP（d）給出了帶有移動因子d的GDEA-IP模型。本文設d=1。

GDEA-IP模型的算法包括以下五個步驟。

步驟1：確定DMU的m種投入，s種產出。

步驟2：確定樣本單元的m種投入，s種產出。

步驟3：根據定義1和定義2，確定投入指標偏好矩陣O和產出偏好矩陣R。

步驟4：解線性規劃。

步驟5：根據效率值V（d）對所有DMU進行排序。

定義1：對于DMUp（p=1，2，…，n），設V（d）為GDEAIP（d）的最優值。如果V（d）≥1，則稱DMUp相對于樣本數據前沿面的d倍移動為弱GDEA-IP有效。

定義2：對于DMUp（p=1，2，…，n），設V（d）為GDEAIP（d）的最優值，ω0和μ0為GDEA-IP（d）的最優解。如果ω0＞0，μ0＞0且V（d）=1或者V（d）＞1，則稱DMUp相對于樣本數據前沿面的d倍移動為強GDEA-IP有效。

定義3：對于DMUp（p=1，2，…，n），設V（d）為GDEAIP（d）的最優值。如果V（d）＜1，則稱DMUp相對于樣本數據前沿面的d倍移動為GDEA-IP無效。

定理：DMU的GDEA-IP有效性與評價指標的量綱選擇無關。

2 考慮指標偏好的廣義DEA模型在長江經濟帶工業綠色發展效率中的應用

本節采用廣義DEA模型和GDEA-IP模型對2016年中國長江經濟帶11個地區的工業綠色發展效率進行測算和排序。

2.1 指標和數據

工業綠色發展效率評價指標包括三種投入指標：資本投入、能源投入和勞動力投入；三種產出指標：一個期望產出和兩個非期望產出。評價指標和數據分別如表1和表2所示，其中非期望產出已通過INP方法進行處理。實證研究的數據來自《2017年中國工業統計年鑒》、《2017年中國城市統計年鑒》、《2017年上海統計年鑒》、《2017年江蘇統計年鑒》、《2017年浙江統計年鑒》、《2017年安徽統計年鑒》、《2017年江西統計年鑒》、《2017年湖北統計年鑒》、《2017湖南統計年鑒》。選取中國長江經濟帶11個地區作為DMU1-DMU11。這11個地區分別是上海市、江蘇省、浙江省、安徽省、江西省、湖北省、湖南省、重慶市、四川省、貴州省和云南省。

表1 投入產出指標

表2 實證研究數據

2.2 結果分析

通過專家評估得，投入指標偏好關系為ω1≥ω2≥ω3，產出指標偏好關系為μ1≥μ2≥μ3。則權重約束矩陣，

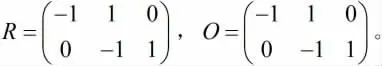
本章廣義DEA模型和考慮指標偏好的廣義DEA模型的算法通過MATLAB軟件編程實現。

首先運用GDEA-IP模型（樣本單元選取為所有決策單元）計算出11個省市的工業綠色發展效率值，結果如表3所示。

表3 基于GDEA-IP模型的效率值

將長江經濟帶11個省市進一步劃分為“東部地區”（DMU1，DMU2，DMU3）、“中 部 地 區”（DMU4，DMU5，DMU6，DMU7）、“西部地區”（DMU8，DMU9，DMU10，DMU11）。計算出每一類地區工業綠色發展效率值的平均值，結果如表4所示。

表4 三類地區的效率平均值

由表4可得，東部地區的效率值的平均值最大，表明東部地區工業綠色發展總體最好，因此選擇東部地區的三個省市作為GDEA-IP模型的樣本單元，進行效率值的進一步測算。表5給出了基于廣義DEA模型和GDEA-IP模型的效率和排名，其中，DMU1、DMU2和DMU3作為樣本單位。

表5 基于廣義DEA模型和GDEA-IP模型的效率值和排序

由表5可知，將權重偏好引入廣義DEA后，54.5%的決策單元的效率值發生了變化，其中DMU11效率值的變化最為明顯，從2.47下降到0.85，從廣義DEA有效變化為GDEA-IP無效。72.7%的決策單元的排名發生了變化，其中原本排名第三名的DMU5上升為第一名，而原本排名第一名的DMU11大幅度下降到第九名。

然而，GDEA-IP得到的排名完全合理嗎？對此，我們選取DMU8，DMU10，DMU11的投入產出數據及效率計算結果進行比較分析，如表6所示。

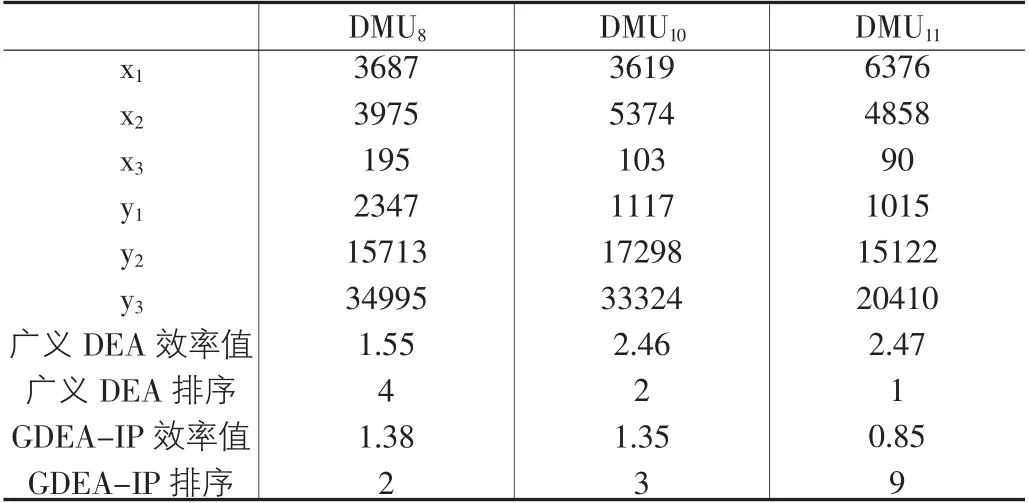
表6 對比分析結果

首先將DMU8和DMU11對比分析。從投入指標的數值上 看，x1（DMU8）＜x1（DMU11），x2（DMU8）＜x2（DMU11），x3（DMU8）＞x3（DMU11）。由于事先約束了x3的權重最小，因此x3對最終效率值的影響最小；從產出指標的數值上看，y1（DMU8）＞y1（DMU11），y2（DMU8）＞y2（DMU11），y3（DMU8）＞y3（DMU11）。根據“投入越少，產出越多的單元效率值越高”的原則，直觀上可看出，DMU8的效率值應該大于DMU11的效率值。廣義DEA模型的計算結果剛好相反，而GDEAIP模型的計算結果是合理的，符合人們的直觀評價。

接著將DMU10和DMU11對比分析。從投入指標的數值上看，x1（DMU10）＜x1（DMU11），x2（DMU10）＞x2（DMU11），x3（DMU10）＞x3（DMU11），并且x1（DMU10）遠遠小于x1（DMU11），減小幅度高達76%，雖然x2（DMU10）大于x2（DMU11），x3（DMU10）大于x3（DMU11），但增加的幅度均小于15%，并且事先約束了x2和x3的權重較小，因此x2和x3對最終效率值的影響較小；從產出指標的數值上看，y1（DMU10）＞y1（DMU11），y2（DMU10）＞y2（DMU11），y3（DMU10）＞y3（DMU11）。同理，根據“投入越少，產出越多的單元效率值越高”的原則，從直觀上可得DMU10的效率值應該大于DMU11的效率值，這與廣義DEA模型的計算結果相反，與考慮權重約束的廣義DEA模型的計算結果相同。

對比分析表明，如果不考慮權重偏好，廣義DEA方法可能會導致不合理的結果，而GDEA-IP模型計算的排序結果更合理，更符合人們的直觀評價。

綜上所述，GDEA-IP不僅可以考慮投入和產出指標的重要程度，而且可以對所有DMU進行全面排序。可見，沒有權重約束的DEA模型是存在缺陷的，只有充分考慮評價指標之間相互影響而客觀存在的共同邏輯關系，并將其納入DEA模型的約束條件才能獲得更科學更合理的結論。

因此，通過分析表5的GDEA-IP模型效率值可得如下結果。從整體來看，長江經濟帶工業綠色發展效率的平均值為1.07，處于DEA有效水平，表明整體效率較高。從東中西部地區來看，三個地區的平均效率值差距相對較小，地區差異不明顯。從每一類地區的內部來看，東部地區的上海市和江蘇省為DEA有效，東部地區內部三個省市效率值差異很小，最大效率值與最小效率值僅僅相差0.05；中部地區的江西和湖南為DEA有效，中部地區內部四個省市效率值差異很大，最大效率值與最小效率值相差高達1.01；西部地區的重慶和貴州為DEA有效，西部地區內部四個省市效率值差異較大，最大效率值與最小效率值相差0.85。

3 結論

通過構建考慮指標約束的廣義DEA模型，對中國長江經濟帶工業綠色發展效率進行分析，得到以下結論：①從整體來看，長江經濟帶工業綠色發展水平較好，整體效率較高，處于DEA有效水平。②分地區來看，東中西三個地區的平均效率值差距相對較小，地區差異不明顯。③從地區內部來看，東部地區內部省市效率值差異很小；中部地區內部省市效率值差異很大；西部地區內部省市效率值差異較大。表明中西部地區發展不均衡、不穩定，政府需采取措施積極推進中西部地區工業綠色轉型，構建協同發展機制，促使各地區協同發展。