基坑開挖對臨近既有單樁承載性能的影響研究

何烈民 HE Lie-min；耿博光 GENG Bo-guang；王思瑞 WANG Si-rui

（①山東省路橋集團有限公司，濟南 250014；②山東大學，濟南 250061）

0 引言

基坑開挖產生的影響大致有三個方面：地下連續墻的變形、坑底隆起和基坑附近地表沉降。地下連續墻的側移還會使基坑底部得土體發生隆起現象[1][2]。當基坑開挖時，由于基坑上方土體被挖出，原有的土體的自重應力消失，因此基坑底部土體會隆起[3]。坑外土體沉降發生之后，樁側阻力受到影響，導致樁身軸力也將發生變化，影響到樁基的承載能力[4]。本文采用數值模擬進行基坑開挖對臨近既有單樁承載性能的影響研究。

1 開挖問題的實現

1.1 ABAQUS中的單元生死功能

ABAQUS能夠在分析步中將單元移除，并且自動計算單元節點力，隨著單元的移除，使節點力逐漸減少直至為零，當移除分析步全部結束后，移除掉的單元對整個模型的影響就全部消失[5]。本文通過該功能來模擬基坑開挖工況。

1.2 初始應力場的建立

巖土工程中碰到的開挖問題,基本上就是隧道開挖與基坑開挖兩種類型，而本文所涉及到的問題是基坑開挖問題,在實際工況中較為復雜，很難有具體的方法來完美分析開挖過程，往往需要用有限元分析軟件來對此問題有一個具體分析。初始應力場的建立十分重要，影響著整個數據模擬過程，因此，如何能夠平衡地應力是首先要考慮到的問題。

真實情況的土體應力極其復雜，很難具體模擬出應力的真實情況，本文通過施加邊界條件和重力荷載模擬地應力的分布[6]，建立與工況大致相同的模型。

2 數值模擬過程

2.1 模型建立及參數選取

選取模型中包括三個部分，分別是土體，地下連續墻，樁體。土體模型選取為90m*90m*40m。基坑為30m*30m*8m，分為四次開挖，每次開挖2m。地下連續墻設置為厚度0.5m，埋深20m。樁半徑為0.5m，樁長20m。土體采用Mohr-Coulomb理想彈塑性本構模型，泊松比取0.35，重度取18kN/m3，初始孔隙比取0.8，單位壓力下土體孔隙比取1.5，回彈指數取0.008，壓縮指數取0.037，臨界狀態應力比取1。地下連續墻，樁體采用線彈性本構模型，重度統一取25kN/m3，彈性模量統一取30GPa，泊松比統一取0.30。

2.2 材料接觸及網格劃分

在本次數值模擬中建立的模型中，樁底與土體的接觸采用tie綁定，樁體的側身與土體定義接觸時，采用Penalty函數模型，摩擦系數設置為0.35。假設地下連續墻在基坑未開挖時就已經存在。地下連續墻與土體之間采用tie綁定，保證土體與地下連續墻之間在開挖之前已經綁定在一起，在開挖進行時，地下連續墻與土體之間具有相同的自由度。

對樁基劃分網格前首先要進行種子布置，在樁周按照數量撒種子，種子數量為三個。網格劃分采用六面體單元，控制屬性為Structure。

2.3 荷載和邊界條件

土體模型上方為自由表面，因此不受到約束。模型左右方向受到X方向的約束，即選擇約束U1。模型前后方向受到Y方向的約束，即選擇約束U2，模型下方受到XYZ三個方向的約束，即選擇約束U1、U2、U3[5]。在地應力平衡步對整個模型施加大小為19kN/m3的體力，模擬出模型在重力作用下的性狀。本文在各物理參數的基礎上，確定在樁基的頂部施加的荷載為5MPa較為合適。

圖1為單樁在基坑無開挖情況下的沉降量云圖，樁頂沉降量10mm，樁底沉降量8mm，大體符合實際情況，證明樁頂施加荷載合理。

3 數值模擬結果分析

3.1 地應力平衡

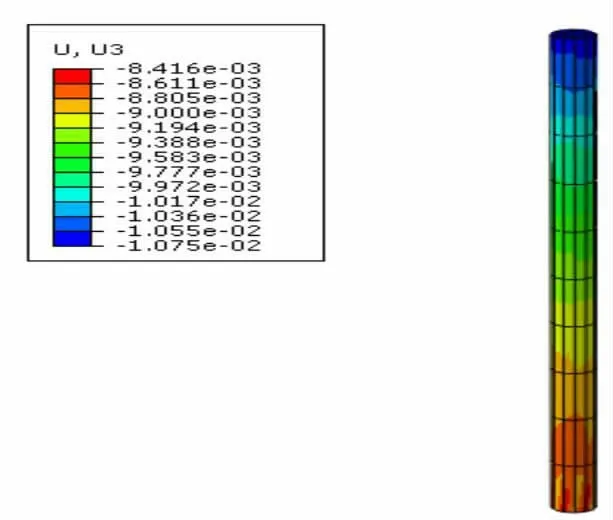
圖1單樁沉降量云圖

圖2 與圖3分別為地應力平衡完后的豎向位移與豎向應力云圖。

圖2 土體豎向位移

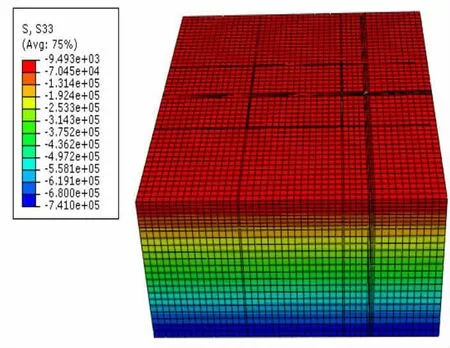
圖3 土體豎向應力

由圖2和圖3可知，地應力平衡后土體的豎向位移的數量級為10-5m，應力的數量級為103N。初始應力與初始位移均比較小，基本與實際相符。

3.2 基坑開挖深度對鄰近樁基的影響

本次開挖過程共計分為四次，每次2m，開挖深度H取值分別為2m、4m、6m、8m通過改變H值來確定基坑開挖對鄰近建筑樁基的影響。不同開挖深度時樁的水平位移見圖4。

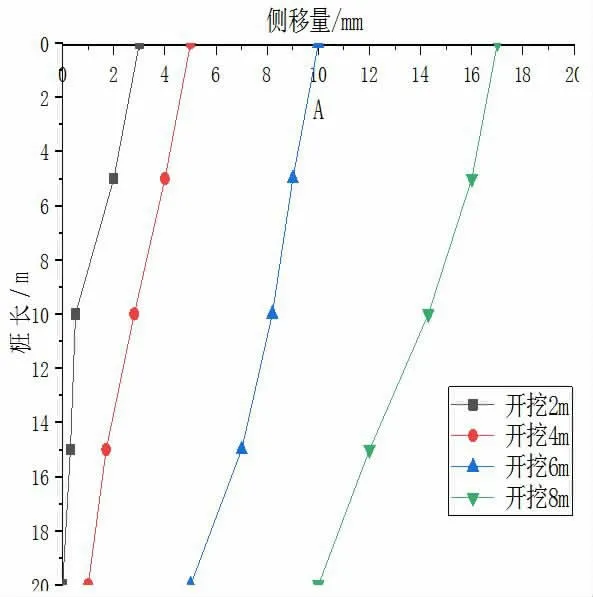
圖4 不同開挖深度時樁的水平位移

由圖4可知，樁基在基坑開挖過程中，當開挖深度為2m時，樁的側移最小，且隨著樁的埋深不斷減小，最大值在樁的頂部，為3mm左右。隨著基坑的不斷開挖，樁的側移不斷增大，當基坑開挖到8m時，樁的側移最大值在樁的頂部，側移量為19mm，且隨著樁的埋深不斷減少，但樁整體側移變化量不大。

不同開挖深度樁的側摩阻力變化見圖5。

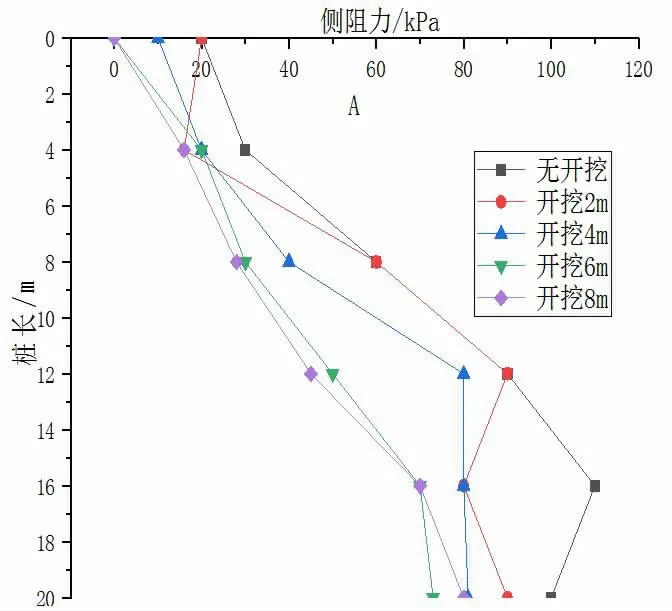
圖5 不同開挖深度樁的側摩阻力變化

由圖5可知，伴隨著土體的開挖，基坑周圍土體發生變形，從而影響到樁的側摩阻力，且開挖深度越大，開挖后基坑周圍土體變形越大，對樁的側摩阻力影響就越大。當無開挖時，樁的最大側摩阻力為110kPa，隨著開挖的的進行，最大側摩阻力分別減少到90kPa、80kPa、70kPa、80kPa。且最大側摩阻力均出現在樁的下部。

基坑開挖深度對樁基彎矩的影響見圖6。

由圖6可知，基坑周圍土體隨基坑開挖而發生沉降和水平變形，進而導致樁基周圍土體也將發生位移，樁體兩側土體性質變得有所不同，在周圍土體的作用下，樁要產生向基坑的彎矩[6]。隨著基坑開挖深度的增加，樁身的彎矩也不斷增加。當基坑開挖深度固定時，樁身的附加彎矩變化變化規律大體是樁頂與樁底較小，樁身中部較大，且彎矩最大值出現在中部。

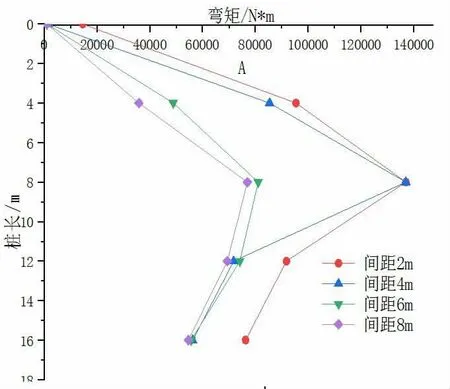
圖6 彎矩隨樁埋深的變化

3.3 樁與基坑的距離對樁基性能的影響

本文將通過設置四種工況，使樁基分別距離基坑2m、4m、6m、8m。基坑開挖深度8m，通過樁的側移、側摩阻力、彎矩等來研究樁基的性能。不同間距時樁的水平位移見圖7。

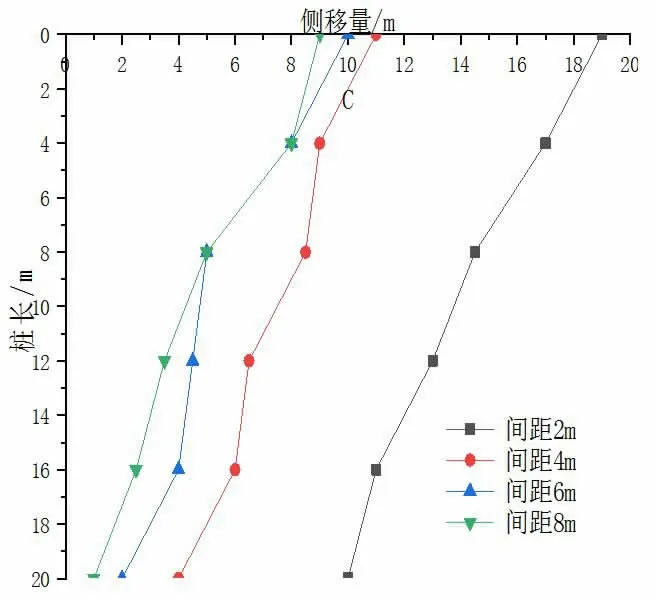
圖7 不同間距樁的水平位移

由圖7可知，當樁與基坑距離為2m時，樁的側移量最小，隨著距離的增大，基坑對樁側移的影響越來越小，當樁與基坑距離在6m和8m時，側移量均小于10mm，此時基坑對樁側移量的影響可以忽略不計。

圖8為開挖深度8m時樁基與基坑的距離對側摩阻力的影響。

由圖8可知，隨著樁與基坑距離的增大，在同等埋深的樁體的側摩阻力均有所增加。這是由于樁與基坑的距離變大，基坑開挖對樁基周圍的土體影響變小，使樁周圍的土體越來越接近無基坑開挖時的狀態。

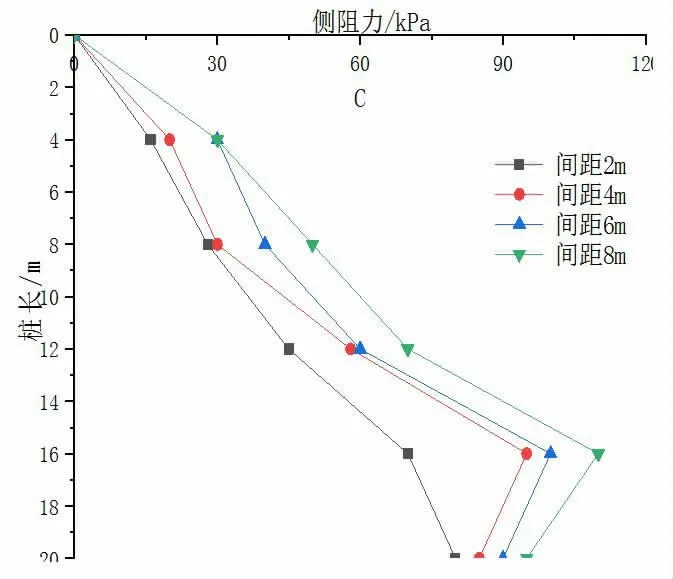
圖8 不同間距樁的側摩阻力變化

開挖深度為8m時樁基與基坑的距離對樁基彎矩的影響見圖9。

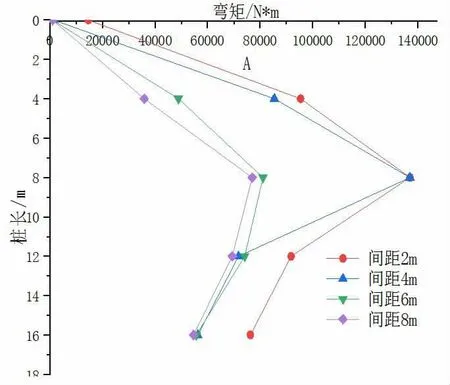
圖9 不同間距樁的彎矩變化

由圖9可知，樁體在遠離基坑的過程中，樁體周圍土體受基坑的影響越來越小，因此樁體的彎矩也在隨著距離的增大而不斷變小。樁身的附加彎矩在樁頂與樁底較小，樁身中部較大，且彎矩最大值出現在中部。

4 結論

采用數值模擬研究基坑開挖對單樁的影響，分析了單樁在受到開挖深度和距離基坑距離影響下的承載特性和變形規律。研究表明，基坑開挖越深，對樁的承載性能和變形影響就越大。樁與基坑開挖的距離越大，對樁的承載性能和變形影響越小。