基于改進Dijkstra算法的輸電線路路徑規劃

張 超，李 欣，趙祥偉

(中國能源建設集團江蘇省電力設計院有限公司，江蘇 南京 211102)

0 引言

輸電線路選線規劃是電網規劃設計的重要內容，傳統的路徑選線通常包括圖上初選、搜資、初勘、設計方案、現場終勘、線路評定等工作[1]。由于前期的搜資和現場勘查需要花費大量的時間、人力和物力，而且搜集到的地理信息常常無法保證時效性和準確性。傳統的選線方法跟專業人員的能力和經驗密切相關，但線路設計考慮的因素和原則常常容易顧此失彼，無法得到最優的路徑[2]。

隨著地理信息技術的快速發展以及智能路徑規劃算法的涌現，輸電線路智能路徑規劃逐漸得到業內人士的關注。余鳳先[3]等應用地理信息系統(geographic information system，GIS)具有的定性、定量、定位分析功能進行九龍—石棉500 kV送電線路的優選工作，朱義中[4]等將層次分析法應用于地理信息系統輸電線路決策支持系統中，實現線路路徑的優選，陳小紅[5]等引入元胞自動機模型，確定輸電線路所要經過的各個元胞及走向，最終形成輸電規劃的路徑，蘇海峰[6-8]等介紹了改進蟻群算法和元胞自動機模型在輸電線路路徑自動選擇中的應用。

Dijkstra算法是目前最短路徑規劃問題的基本算法，已廣泛應用于公路、鐵路、輸電線路、油氣管道等的路徑規劃中。本文采用專家決策法確定地圖柵格綜合成本，并通過限制目標搜索區域，減少無意義運算，提高Dijkstra算法搜索效率，能有效改善輸電線路路徑規劃的效果。

1 Dijkstra算法

1.1 基本原理

Dijkstra算法是荷蘭科學家狄克斯特拉于1959年提出的啟發式搜索方法，故也叫狄克斯特拉算法。其基本思想是：從頂點V0出發，搜索從它到其他各頂點的最短路徑。把有向圖中的頂點集V分成兩個子集S和T，S為已求出最短路徑頂點的集合，T為尚未求出最短路徑的頂點集合；循環遍歷集合T，每次找出最短路徑的頂點放入集合S中，直到集合T為空。

圖1 Dijkstra算法示意圖

如圖1所示，設帶權有向圖G={V，E}，V=V0，V1，…Vn-1，用帶權的鄰接矩陣Arc表示 圖G；Arc[i][j]表 示 弧 (Vi，Vj)上 的 權 值，S表示已求出以為起點的最短路徑終點的集合；向量D的每個D[i]表示當前求得的從起點V0到每個頂點Vi的最短路徑的長度，利用Dijkstra算法從源點s到終點t的步驟如圖2所示。

圖2 Dijkstra算法流程圖

不同于圖論和矢量GIS的傳統線型網絡最優路徑搜索，基于柵格地形的最優路徑搜索可以作為虛擬柵格網絡的最優路徑搜索，是一種格網鄰域模型的路徑搜索。根據柵格單元隱含的鄰接關系，柵格數據模型可以通過連接相鄰的節點來抽象成柵格網絡。目前常用的格網鄰域模型有四、八和十六格網鄰域結構，其中八鄰域模型不僅具有復雜度低，而且精確度高、時間性能好等優點，本文采用八鄰域結構(如圖3所示)。

圖3 八鄰域模型結構圖

八鄰域模型實現Dijkstra算法的過程如圖4所示。

圖4 Dijkstra八鄰域模型算法流程圖

1.2 算法改進

Dijkstra算法能夠計算出兩點之間最短路徑的最優解，而且魯棒性很強，但隨著節點數量的增大，它的計算效率會降低。由1.1節可知，Dijkstra算法采用帶權的鄰接矩陣存儲圖形數據，占用大量內存空間；并且它是一種盲目或無向搜索算法，對于具有n個節點的圖，它的算法時間復雜度為O(n2)，計算時間和存儲開銷都比較大。本文采用限制搜索區域[9]加載部分柵格模型，提高搜索效率，降低搜索時間。

Dijkstra算法的搜索過程類似于以起點為圓心不斷向外擴展的一系列同心圓，是一種無向搜索，它沒有考慮終點所在的位置或方向，因此在不斷向外搜索的過程中，其他頂點與終點被搜索到的概率相同。當起點和終點距離較遠時，會產生大量無意義的搜索，降低搜索效率，收斂時間大大增加。起點到終點之間除了距離關系外，還有方向的關系，兩點之間的直線線段代表了最短路線的趨勢方向，即最短路徑順著這個趨勢方向的概率極大。因此，為了減少無意義的搜索，以起點和終點作為矩形區域對角線的兩個頂點，只遍歷矩形范圍內的柵格。當發生矩形內的路徑被障礙物阻擋而需繞至矩形外的情況時，本文采取的方案是逐步擴大矩形的范圍，直到搜索到最優路徑。

1.3 模擬實驗

圖5中紅色圓圈代表障礙物，藍色米字代表起點，紅色米字代表終點。為了提高搜素效率，通過在周邊設置障礙物的方式，阻止或減少無效的路徑尋找。

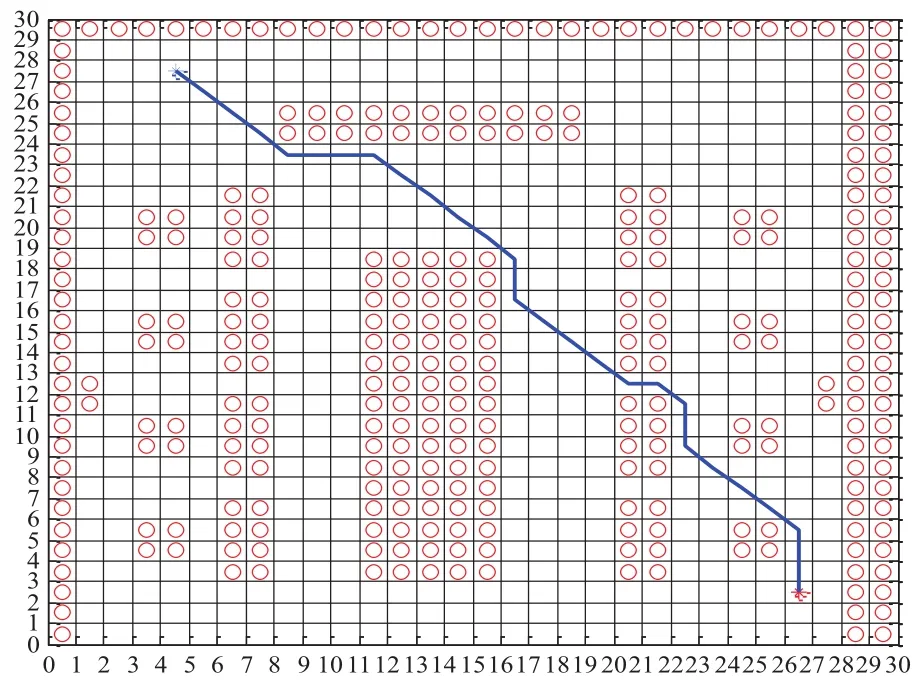
圖5 模擬最短路徑

2 輸電線路智能選線Dijkstra算法建模

2.1 柵格數據準備

由于線路設計人員搜集到的資料通常都是遙感影像，而Dijkstra算法搜索最短路徑是建立在柵格基礎上的，所以需要對遙感影像進行柵格化處理。進行柵格化之前，需要對遙感影像進行地物分類，如房屋、道路、河流、農田、林地等，根據這些環境因素對輸電線路選線的影響程度分別賦予不同的權重。

2.2 路徑成本計算

Dijkstra算法采用“節點/聯系”模型來表達，每個柵格被認為是一個節點，兩個相鄰節點用“聯系”來連結，這個“聯系”被表示為成本或代價。由于使用八鄰域模型，故從某個節點出發會有8個方向，這8個方向又可分為兩類，直線方向(上下左右)和斜線(對角)方向。每個柵格都被賦予相應的權重值，即線路經過此柵格的成本代價，用costi(i為柵格編號)表示。如圖1中直線方向的“聯系”值就是相鄰兩個柵格成本的平均值，如A、B兩點間的聯系成本為costAB=(costA+costB)/2，A、C兩點間的聯系成本為costAC=1.414×(costA+costC)/2，A、E兩點間的累計聯系成本為costAE=costAC+1.414×(costC+costE)/2。

從源點到終點，產生累計成本柵格數據以找到最佳路徑，就是一個從源柵格開始向外探索的過程。如從源柵格A出發，首先搜尋相鄰的東、西、南、北、東北、西北、東南、西南幾個方向的8個柵格，用上面的公式計算相應的聯結成本。由于這8個鄰域柵格均可以到達源柵格，所以將他們放入OPEN列表中，然后對這8個柵格逐一擴展，將他們的鄰域柵格加入OPEN列表，同時將這8個柵格加入CLOSE列表，代表已經遍歷完畢。源柵格不一定要求是相連的，所有不相鄰的柵格對于OPEN列表的貢獻是相等的，只有具有最低成本的柵格才會被選擇，其鄰域柵格才可以被擴展，而無需考慮是從哪個源柵格開始計算的。逐漸向外擴展的過程中，如果發現某柵格有多個后向聯結柵格，那么將具有最低聯結成本的柵格安排到CLOSE列表中。計算累計成本時，這些成本也會計算新的被列入CLOSE列表中的柵格成本值，即使鄰域柵格是從另外一個源柵格開始計算的。如果新的累計成本值比當前值大，則該值不計入；如果新累計值小，則當前位置柵格的累計成本會被新累計值代替，這表明根據新柵格發現了成本更低的一條路徑，所以將其安排進CLOSE列表。如果擴展柵格有多個源柵格，擴展過程將繼續將最低成本柵格加入到OPEN列表中，而不用顧及是從哪個柵格開始的，直到找到最終的最低成本也就是最優路徑。

3 實例分析

3.1 實驗數據來源及處理

本文采用的實例數據來源于江蘇某220 kV線路工程，如圖6所示，該線路地處江蘇北部平原地帶，地勢平坦，地物以田地、房屋、道路、河道為主。因為輸電線路跨越房屋會產生較大的拆遷賠償費用，故線路設計原則上盡量不跨越房屋，道路上不允許立塔，河道尤其是通航河道立塔條件較差，一般情況下田地最適合立塔。基于上述分析及專業工作經驗，本文對田地、房屋、林木、河流賦予的權重或成本值分別為1、4、3、2。

圖6 實驗區域的影像

首先對遙感影像進行矢量化，該過程也是一個地物分類的過程，本文將該區域的地物分為田地、房屋、林木、河流4類，如圖7所示，其中淺綠色表示田地，粉色表示房屋，深綠色表示林木，藍色表示河流。每種地物矢量化后，在屬性表中添加權重值的屬性。分類結束后，需進行柵格化，考慮到柵格邊長太長，會導致分辨率低，地物抽象失真；柵格邊長太短，會導致分辨率過高，柵格數量過多，搜索過程過長，因此柵格邊長應取值適當，本文將柵格的邊長為50 m。劃分柵格以后，將每個柵格的權重屬性賦予柵格中心，這樣就完成了路徑搜索前的數據準備工作。

圖7 矢量化后的效果圖

3.2 選線結果分析

設置起點和終點，并限制優先搜索區域，便可以進行最短路徑尋找，結果如圖8所示。可以看出，該路徑避開了房屋和林木，而且距離較短，基本符合最優路徑要求。

圖8 最短路徑柵格效果圖

傳統的Dijkstra算法耗時2.61 s，改進后的Dijkstra算法路徑搜索效率耗時為1.82 s，相比傳統算法提高了30%，效果顯著。算法效率的提高程度與路徑起終點在整幅圖中的分布位置有關，當兩個點在圖的中間位置時，效率改善程度最高；在對角位置時，改善程度最低。

在很多情況下，運用智能路徑規劃算法得出的路徑往往還需要進行適當的人工干預，因為在實際的輸電線路工程中，要考慮的因素不止本文中所提到的幾種，還包括地質、覆冰以及轉角數量等很多其他因素。

4 結語

輸電線路路徑設計是一個復雜耗時的工作，結合地理信息技術能夠大幅提高線路路徑設計效率。本文使用地理信息技術，將遙感影像分類并柵格化，采用智能路徑規劃Dijkstra算法，并使用MATLAB編程實現，在輸電線路設計工作中取得了不錯的效果。進一步地以線路起點和終點作為矩形區域對角線的兩個頂點，只遍歷矩形范圍內的柵格，減少無意義的耗時搜索，效率比傳統算法提升30%，改善效果顯著，能夠在輸電線路選線設計中發揮較大的作用。