主給水調節閥節流窗口周向設計及其對流動特性的影響

吳嘉懿，岳 陽，李軍業，金志江，錢錦遠

（1.浙江大學化工機械研究所，浙江 杭州 310027；2.中核蘇閥科技實業股份有限公司,江蘇 蘇州 215129）

隨著世界能源需求逐年穩步增長和全球環境持續惡化，以核電為代表的清潔能源愈發引起普遍關注［1-2］。《中國能源中長期（2030、2050）發展戰略研究》指出［3］，積極發展核電是我國能源長期重大戰略選擇。

在核電站中，一回路內的載熱工質不斷將反應堆產生的熱量傳入蒸汽發生器，二回路內的給水在蒸汽發生器中持續吸收熱量而蒸發，并最終推動汽輪機發電［4-6］。安裝于二回路的主給水調節閥是控制給水流量、維持蒸汽發生器水位高度平穩的關鍵設備，其流動特性影響著核電站的運行安全與效率［7-8］。

近些年來，在“以國代進”的背景下，我國相關閥門生產企業和研究院所針對主給水調節閥開展了技術攻關。宋輝［9］根據壓水堆核島機械設備的設計和建造規則總結了主給水調節閥的4個設計要點：1）大推力執行機構的設計驗證；2）節流窗口的優化設計及試驗；3）閥門控制精度的把控；4）閥門抗震鑒定試驗。Qian等［10］通過構建無量綱系數來描述節流窗口形狀，繼而展開全面的數值計算，獲得了基于節流窗口形狀系數的主給水調節閥流量特性函數。沈國強等［11］對一款主給水調節閥進行了抗震分析，發現支架立板厚度和支架高度對閥門整體結構頻率的影響最為明顯。同時，Wu等［12］分析了一款主給水調節閥在不同載荷組合作用下的模態和結構，發現地震載荷會使其最大位移約增大3倍。

核電廠相關技術人員也根據實踐經驗，對主給水調節閥的設計和制造提出了指導意見。例如，針對主給水調節閥在手動操作狀態下出現超調和滯后現象，并引發流量波動的問題，周廣靈［13］指出閥門的閥位指示桿與閥門支架緊貼導致閥桿摩擦力過大是問題的根源。

針對閥門及類閥設備的研究，也為主給水調節閥的設計提供了參考。崔寶玲等［14］分析了閥芯結構對節流截止閥流阻特性的影響，發現弧形閥芯可使閥門流量隨開度的變化更為均勻，更有利于閥門流量的調節。張曉東等［15］通過仿真發現，在一種類閥的新型內防噴器中，沖蝕磨損部位主要發生在閥座流道邊緣，并提出減少沖蝕磨損的閥座最優錐角為25°。Chern等［16］、于靜梅等［17］分別探討了節流孔結構對套筒閥流量特性和節流特性的影響，前者發現僅改變內套筒上的節流孔尺寸及排布即可使閥門流量特性自線性改變為二階多項式形式，后者發現具有迷宮彎折型節流孔排布的套筒表現出最優的降壓與降速能力。Pan等［18-19］通過AMESim、ADAMS、UG與MATLAB的協同仿真來輔助主給水調節閥及主蒸汽調節閥執行結構的設計，并提出了確定對應于最優動作性能的最大壓力的無量綱目標函數。

雖然目前對主給水調節閥尤其是對基于流通能力的節流窗口的設計已有一定的研究，但是對節流窗口設計對閥門流動特性的影響的研究還不夠深入，未能從保持閥門流通能力不變而改善其流動特性的角度對主給水調節閥進行優化設計。因此，本文基于數值模擬方法探討了節流窗口周向設計對主給水調節閥流動特性的影響。提出了無量綱的節流窗口周向布置不平衡度，并討論其對閥芯不平衡力矩和閥門流量系數的影響，以期為主給水調節閥及其他類似閥門的設計與優化提供一定的參考。

1 研究方法

1.1 節流窗口周向設計方法

主給水調節閥的結構如圖1所示。其主要由閥桿、閥蓋、墊片、閥芯、套筒、閥體等零部件組成。閥體通徑為DN200。套筒周向與閥芯緊密接觸，其上開設有節流窗口。在主給水調節閥工作過程中，閥芯在閥桿的推動下沿軸向運動，從而改變節流窗口或節流孔的開放面積，進而實現流量調節功能。

主給水調節閥套筒的展開圖如圖2所示。其上開設的節流窗口呈上大下小的漏斗形。套筒關于閥門縱剖面（對應于圖1坐標系O-XYZ中的XOY面和圖2中的Y軸）對稱。其中：XOZ面與套筒底面重合，原點O設置在套筒底面中心，Y軸平行于閥桿指向閥門正上方；在套筒一側自閥門出口方向至閥門入口方向的節流窗口的序號l分別為1，2，3；tl和bl分別為節流窗口頂部邊長和底部邊長；wc為相鄰兩節流窗口之間的最小間隔。基于常見的節流窗口周向平衡布置方式（即套筒上各節流窗口截面形狀相同，如圖2（a）所示），本文提出通過調整各節流窗口頂部邊長，將節流窗口在套筒周向進行非平衡布置（即套筒上各節流窗口截面形狀不相同，如圖2（b）所示）。

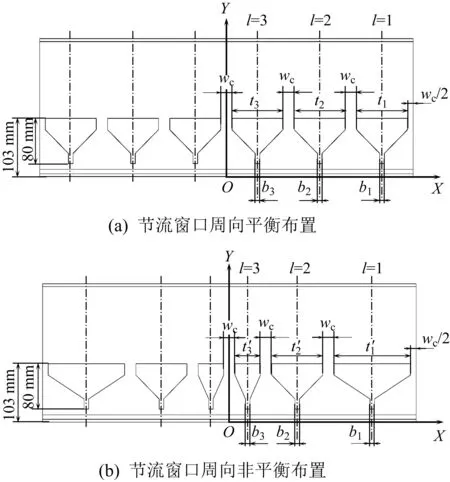
圖2 主給水調節閥套筒的展開圖Fig.2 Expanded view of MFWRV sleeve

在節流窗口周向非平衡布置的套筒中，各節流窗口頂部邊長為：

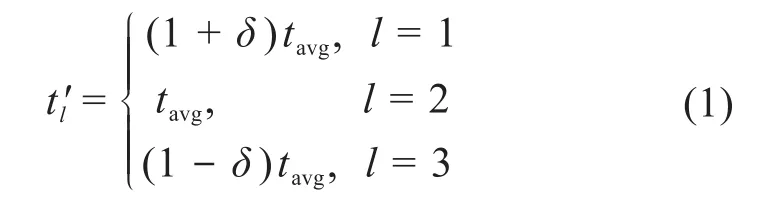
式中：tl′為非平衡布置后各節流窗口頂部邊長；tavg=（t1+t2+t3）/3，為節流窗口頂部邊長平均值；δ為節流窗口周向布置不平衡度，在本文中取δ∈［-0.5，0.5］。

1.2 數值模擬方法及實驗驗證

以140°C的高溫水作為主給水調節閥流通介質，其密度為 926.1 kg/m3，動力黏度為 0.000 201 Pa·s。閥門入口壓力為7.5 MPa，出口壓力為7.2 MPa，不考慮壁面與水之間的滑移。基于通用求解器ANSYS Fluent 17.2，采用數值模擬方法，結合雷諾平均N-S（RANS）方程與Realizable k—ε湍流模型來描述閥內流體的流動。RANS方程如公式（2）和公式（3）所示，Realizable k—ε湍流模型如公式（4）至公式（11）所示。

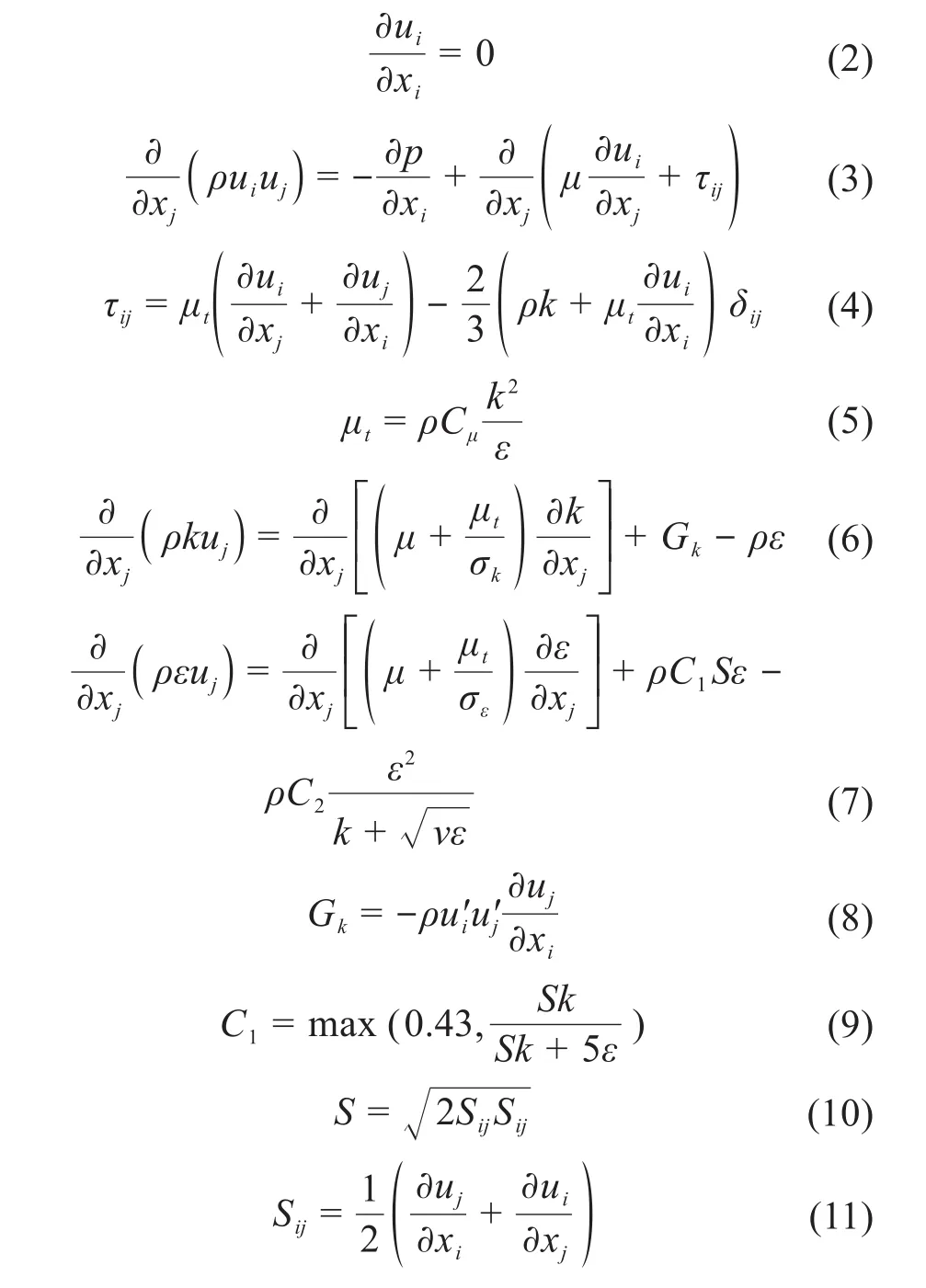
式中：u為流體的速度，m/s；ρ為流體的密度，kg/m3；p為流體的壓力，Pa；μ為流體的動力黏度，Pa·s；τij為流體的雷諾應力，MPa；μt為流體的湍流黏性，kg/（m·s）；k為流體的湍動能，m2/s2；δij為克羅內克符號；ε為流體的湍流耗散率，m2/s3；Cμ為與平均應變、旋轉速率、系統旋轉角速度、湍動能和湍流耗散率相關的系數；C2為常數；σk、σε分別為k和ε的湍流普朗特數；ν為流體的運動黏度，m2/s。

采用六面體網格對流域進行離散化，如圖3所示。離散時，額外考慮了閥門上、下游管路內的流域以減小邊界條件對計算結果的影響。全流域在X、Y、Z方向上的尺寸分別為1 394，345和200 mm。在數值模擬過程中，離散方程依照Simple算法進行計算，節點間的插值計算遵循First Order Upwimd格式，近壁面附近流場采用Standard Wall Function求解。本文以流量系數Cν為判據，對網格無關性進行驗證。Cν用于衡量閥門的流通能力，根據GB/T 30832—2014，其定義如下：

圖3 流域的離散模型Fig.3 Discrete model of flow region

式中：Q為給水體積流量；Δp為閥前后壓差；ρ0為15°C水的密度，ρ0=998.95 kg/m3。

基于GCI（grid convergence index method，網格收斂指數）方法［20］，采用3套數量差異顯著的網格對δ=0、L/Lmax=100%的流域離散模型進行計算。其中，L/Lmax為閥門開度，L為閥芯行程，Lmax為閥芯最大行程。網格無關性驗證結果如表1所示。其中：d為GCI法的顯性階數；ea為第1套網格與第2套網格所對應的Cν之間的近似相對誤差；G2為基于第2套網格的收斂指標。因此，采用第2套網格時，計算的數值不確定度為3.63%，這在工程應用中是可以接受的。因此，采用第2套網格所對應的離散策略進行仿真計算。

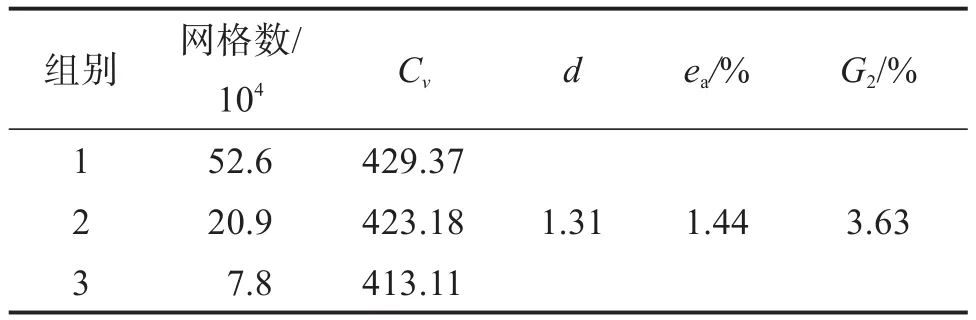
表1 流域離散模型網格無關性驗證結果（δ=0,L/Lmax=100%）Table 1 Verification results of grid independence of watershed discrete model(δ=0,L/Lmax=100%)

此外，進行通徑為DN550的主給水調節閥的流量實驗，以對數值模擬結果的準確性進行驗證。主給水調節閥流量實驗的裝置如圖4所示。其主要由水泵、水箱、緩沖罐、截止閥、測試閥、流量計、壓力計、循環管路、管長調節機構等部件組成。流量仿真結果與實驗結果的對比如圖5所示。其中，E為仿真結果相對于實驗結果的相對誤差。由圖5可知：最大相對誤差出現在L/Lmax=30%時，其值為-26.45%；當L/Lmax≠ 20%～40%時，E＜20%。總體的平均相對誤差為11.82%。因此，可以認為所做的數值模擬是準確可靠的。

圖4 主給水調節閥流量實驗的裝置Fig.4 Device for MFWRV flow test

圖5 主給水調節閥流量仿真結果與實驗結果的對比Fig.5 Comparison between simulation results and experimental results of MFWRV flow

2 結果與討論

2.1 閥內流場特性

主給水調節閥閥內流場的速度云圖和流線圖如圖6所示，壓力云圖如圖7所示。高溫水自入口流入主給水調節閥后，先經入口流道向下進入閥門下腔，然后向上進入閥門中腔；在閥門中腔，高溫水分離為6股水流，分別經6個節流窗口進入閥門環形腔；在閥門環形腔與出口流道連接處6股水流匯合，并經出口流道流出主給水調節閥。

圖6 主給水調節閥閥內流場的速度云圖和流線圖Fig.6 Velocity nephogram and streamline diagram of flow field in MFWRV

由圖6（a）可知，閥門中腔存在著一個顯著的低速渦旋。這個渦旋的出現源于高溫水在從閥門下腔到靠近閥門入口的2個節流窗口（即圖2中序號為3的節流窗口）的流動過程中發生的近180°的轉向。

由圖6（a）還可知，3個節流窗口均為高速流動區，這是因為節流窗口是閥內流道流通面積最小的。同時還可以發現，自面向閥門出口的節流窗口（即圖2中序號為1的節流窗口）至面向閥門入口的節流窗口（即圖2中序號為3的節流窗口），其高速流動區逐漸減小，這是因為節流窗口后環形流道的存在使得流體在從6個節流窗口經環形流道到出口流道的流動過程中所受阻力不同。流體從靠近閥門出口的節流窗口（即圖2中序號為1的節流窗口）流向出口流道時，在環形流道中轉向幅度最小，流道流阻最小，因此高速區最大。而流體從靠近閥門出口的節流窗口（即圖2中序號為3的節流窗口）流向出口流道時，在環形流道中轉向幅度最大，流道流阻最大，因此高速區最小。

由圖7（b）可知，閥芯底面壓力呈現不均勻分布，即靠近閥門出口處的壓力明顯高于靠近閥門入口處的壓力。這種不均勻的壓力分布會對閥芯產生不平衡力矩，使閥芯產生傾覆趨勢并增大閥芯與套筒之間的摩擦力。因此，由不均勻的壓力分布引起的不平衡力矩會加劇閥芯與套筒之間的磨損，并可能引發主給水調節閥閥芯動作卡滯，縮短閥芯和套筒的工作壽命。

2.2 閥芯不平衡力矩

主給水調節閥關于XOY平面對稱，故閥芯底面不均勻的壓力分布不會引發相對于X軸的不平衡力矩。而閥芯底面垂直于Y軸，不均勻的壓力分布也不會引發相對于Y軸的不平衡力矩。因此，閥芯底面不均勻的壓力分布僅會引起相對于Z軸的不平衡力矩。

閥芯不平衡力矩M的計算公式如下：

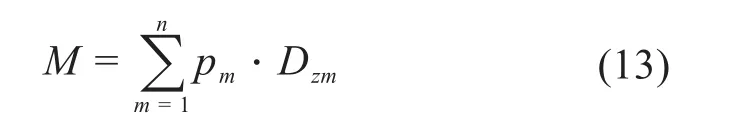
式中：pm為第m個節點的壓力；Dzm為第m個節點到Z軸的距離；n為節點數。

節流窗口周向布置不平衡度對閥芯不平衡力矩的影響如圖8所示。其中，EM為各δ所對應的M值相對于δ=0時的相對誤差。由圖可知：隨著δ從-0.5逐漸增大至0.5，M先增大后減小；δ＞0時的M值均小于δ=0時，δ＜0時的M值大于δ=0時；當δ=-0.2或δ=-0.3時，M達到最大值，此時EM=4.27%；當δ=0.5時，M達到最小值，此時EM=-22.10%。這說明，通過調整節流窗口周向布置方式可以有效改變閥芯底面的壓力分布，從而改變閥芯不平衡力矩。

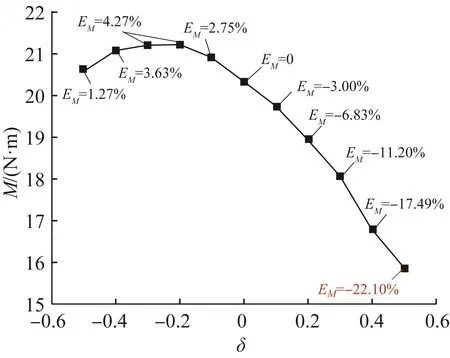
圖8 節流窗口周向布置不平衡度對閥芯不平衡力的影響Fig.8 Influence of unbalance degree of circumferential arrangement of throttling window on unbalance force of valve core

當δ=0，0.5時，不同閥門開度下閥芯不平衡力矩的變化如圖9所示。由圖可知：隨著L/Lmax增大，δ=0時M逐漸增大，δ=0.5時M先在小范圍內波動，后快速增大；M的最大值均出現在L/Lmax=100%時，即閥門最大開度時；當δ=0時，M的最小值出現在L/Lmax=10%時；當δ=0.5時，M的最小值出現在L/Lmax=40%時；當L/Lmax=10%～30%時，δ=0時的M值小于δ=0.5時，但M值均接近于0 N·m，兩者的差距較小；當L/Lmax=40%～100%時，δ=0時的M值大于δ=0.5時。可見，當L/Lmax＜40%時，δ=0與δ=0.5所對應的M值基本一致，此時調整節流窗口周向布置方式對閥芯不平衡力矩的影響較小；而當L/Lmax＞40%時，δ從0增大到0.5，則M值顯著減小，此時可以通過調整節流窗口周向布置方式來有效改變閥芯不平衡力矩。

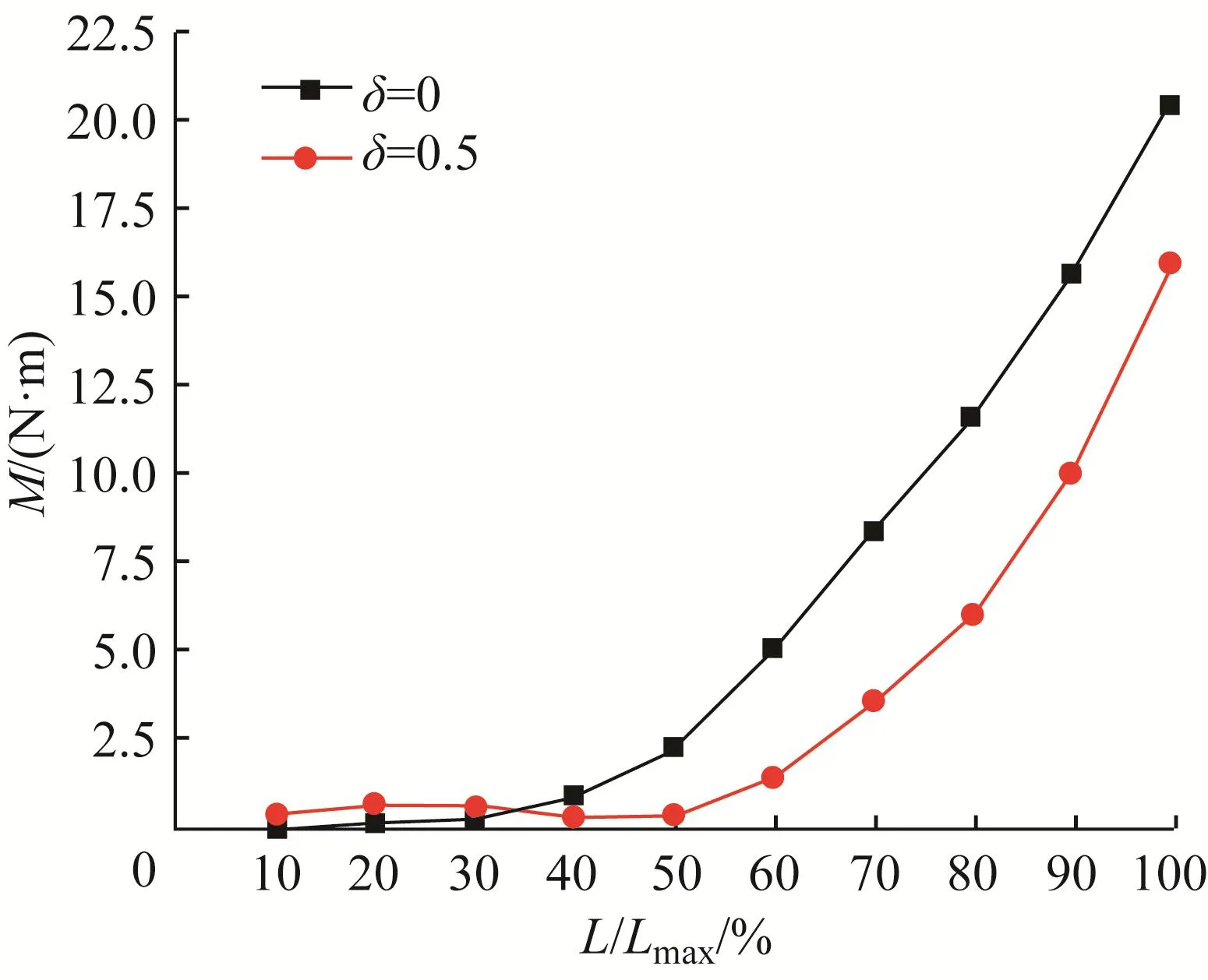
圖9 不同閥門開度下閥芯不平衡力矩的變化Fig.9 Variation of unbalance torque imposed on valve core under different valve opening

2.3 閥門流量系數

節流窗口周向布置不平衡度對100%閥門開度時流量系數的影響如表2所示。其中，ECν為各δ所對應的Cν值相對于δ=0時的相對誤差。由表可知：隨著δ從-0.5逐漸增大至0.5，Cν先增大后減小；當δ=-0.2時，Cν達到最大值，此時ECν=0.39%；當δ=0.5時，Cν達到最小值，此時ECν=-2.74%。總體來說，δ對Cν的影響并不顯著。這是因為，當δ變化時，套筒的6個節流窗口的流通總面積并不變。結合圖8可知，通過將δ從0增大至0.5，可以在保持閥門流通能力基本不變的情況，顯著減小閥芯不平衡力矩。

表2 節流窗口周向布置不平衡度對100%閥門開度時流量系數的影響Table 2 Influence of unbalanced degree of circumferential arrangement of throttling window on flow coefficient at valve opening of 100%

當δ=0，0.5時，不同閥門開度下流量系數的變化如圖10所示。由圖可知：當δ=0，0.5時，Cν均隨著L/Lmax的增大而增大。這是因為，隨著L/Lmax的增大，節流窗口逐漸打開，其流通面積逐漸增大，閥門流阻逐漸減小。同時，當L/Lmax=10%～70%時，Cν值幾乎相同。僅當L/Lmax=80%～100%時，兩者略有差別，且隨著L/Lmax的增大，兩者的差別逐漸增大。

圖10 不同閥門開度下流量系數的變化Fig.10 Variation of flow coefficient under different valve opening

3 結論

基于常見的節流窗口周向平衡布置的套筒，通過調整各節流窗口頂部邊長，將節流窗口在套筒周向進行非平衡布置，并提出了節流窗口周向布置不平衡度δ，進而通過數值模擬方法定量探討了節流窗口周向布置方式對主給水調節閥流動特性的影響。數值模擬方法的有效性通過主給水調節閥流量實驗進行了驗證。

通過分析得出如下主要結論：閥芯底部不均勻的壓力分布會對閥芯產生不平衡力矩，使閥芯產生傾覆趨勢并增大閥芯與套筒之間的摩擦力，進而加劇閥芯與套筒之間的磨損，可能引發主給水調節閥閥芯動作卡滯，并使閥芯和套筒的工作壽命縮短；當閥門開度小于40%時，調整節流窗口周向布置方式對閥芯不平衡力矩的影響較小；當閥門開度大于40%時，通過調整節流窗口周向布置方式可以有效改變閥芯不平衡力矩；在相同條件下，通過將節流窗口周向布置不平衡度從0增大至0.5，可使最大閥芯不平衡力矩減小22.10%，而閥門流量系數僅減小2.74%。