基于緩沖阻尼的空間大慣量負載驅動系統的研究

楊新海，沈曉鵬，趙繼亮，謝 哲，苑會領

（1.上海宇航系統工程研究所，上海 201109；2.上海市空間飛行器機構重點實驗室，上海 201109）

由于空間失重效應，飛行器在軌工作時的負載對象大部分為慣性負載。轉動慣量是慣性負載的主要形式，較大的轉動慣量達到104～106kg·m2。例如：在空間站組裝過程中，飛行器艙體須進行轉動［1-3］，則艙體的轉動慣量達到 106kg·m2［4］，較之于地面的大慣量負載高出幾個數量級，如一般測控雷達的轉動慣量僅為 103kg·m2［5］。超大的轉動慣量要求艙體轉位機械臂的驅動關節具有較強的負載驅動和制動能力［6］。地面工程機械所采用的液壓伺服系統雖然可以實現超大慣量負載的驅動［7-8］，但其存在功耗和質量過大、空間環境適應性差等問題，不適用于空間飛行器。若采用電機直驅的方式來實現大慣量負載平穩且精確的運動控制，則需要一個超大功率的電機，且必須具有能與大負載慣量相匹配的轉子轉動慣量［9-10］，這與空間機構對驅動系統功率和質量的嚴格限制相矛盾。文獻［11］提出了一種基于全閉環+模糊自適應PID（proportion-integration-differentiation，比例-積分-微分）的控制方法，利用伺服電機實現了大慣量轉臺系統較高的響應速度和控制精度，但該控制方法相對復雜，工程應用的可靠性不夠高，且所研究對象的轉動慣量依然較小，對于超大慣量負載驅動的工程可復制性有待驗證。利用現有較為成熟的技術只能實現負載轉動慣量僅為電機轉動慣量幾倍的電機調速控制［12-14］。

此外，由于缺少輔助機構如齒輪、帶輪等的傳動，電機直驅方式會在不確定條件因素下對驅動系統帶來伺服控制的波動，包括力矩紋波、參數變化、外部擾動、自身非線性和無法模型化的動力學特性［15-17］。

增大驅動系統的機械減速比固然可以降低電機端的等效負載慣量，然而超大的減速比會嚴重影響驅動機構的效率和系統頻響特性，這對需要在地面快速作業的機器人來說是致命的缺點。相反，不同于地面機械裝置如工業機器人，空間飛行器不需要較優的頻響特性，但在功耗和質量方面受到嚴格限制。為了保證飛行器的安全和穩定，可以采用以小功率驅動大負載即以時間換能量的方式，通過延長啟動時間和制動時間實現較為平穩的啟動和制動。

緩沖阻尼技術已經廣泛應用于航天器的研制中。如可控阻尼器已經成功用于空間交會對接機構［18-19］，在飛行器對接緩沖過程中，起到了關鍵的慣性動能緩沖和消耗的作用。基于該技術的應用背景，筆者以空間站組裝過程中轉位的艙體為研究對象，應用空間飛行器機構的緩沖阻尼技術，建立具有多級齒輪傳動、彈簧緩沖、阻尼器耗能及電磁制動等功能的驅動系統，以實現在空間站實驗艙艙體轉位過程中超大慣性負載的平穩驅動和精確制動。

1 大慣性負載驅動系統的模型

1.1 驅動原理

驅動機構傳動鏈分為驅動主路、驅動支路、緩沖支路和耗能支路四部分，如圖1所示。驅動主路和驅動支路構成驅動基本傳動鏈路，驅動主路并聯于緩沖支路和耗能支路，實現集成緩沖阻尼功能。驅動支路包含驅動電機和減速器。驅動主路與各支路之間通過齒輪傳動連接和傳遞載荷。

1.2 參數設計

根據平穩啟動的特性要求來確定總傳動比。首先根據驅動機構制動時的負載慣量和阻尼衰減的振動幅值確定驅動機構的緩沖阻尼參數，然后確定各組件之間的傳動比分配關系。在空間站組裝過程中，艙體轉位運動總轉動慣量為2.2×106kg·m2，據此選定空間交會對接機構使用的J36直流無刷電機、彈簧機構和電磁阻尼器，采用雙電機驅動、雙阻尼器耗能的工作模式。要求啟動過程運行平穩，制動振幅小，且緩沖衰減快。

1.2.1 總傳動比的確定

驅動機構各組件之間的傳動比關系如圖2所示。其中i1、i2、i3分別為電機到彈簧機構、彈簧機構到末端輸出、彈簧機構到阻尼器的傳動比。

圖2 驅動機構各組件之間的傳動比關系Fig.2 Transmission ratio relationship between components of driving mechanism

由電機啟動時間的經驗公式分析啟動扭矩、轉動慣量和啟動阻力矩之間的關系：

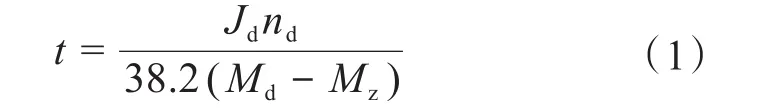
式中：t為電機轉子的啟動時間，s；Jd為電機轉子端等效轉動慣量，kg·m2，Jd=J/i，J為輸出端轉動慣量，i為總傳動比；nd為電機額定轉速，r/min；Md為電機額定力矩，Mz為啟動阻力矩，N·m。

由于Mz?Md，可予以忽略，則在雙電機工作模式下，有：

已知J=2.2×106kg·m2，nd=2150r/min，Md=0.035N·m，要求啟動時間 t≤0.2 s，求得i≥233 826，可取值為235 000。考慮到電機空載轉速較額定轉速高30%，則驅動機構的角速度ωmax≈0.14°/s。

1.2.2 等效剛度和等效阻尼系數的設計

帶緩沖阻尼特性的驅動機構的傳動鏈結構復雜，傳動空程、傳動效率、摩擦阻尼、彈簧回滯特性等非線性因素對驅動機構運動特性的綜合影響無法用準確的數學模型來描述。因此，用等效剛度和等效阻尼來系統描述機構的運動特性。

1）等效剛度。

彈簧機構的特性曲線如圖3所示，驅動機構的等效剛度特性曲線如圖4所示。其中：k為驅動機構回轉結構的等效傳動剛度，包括彈簧機構本身的結構剛度和齒輪傳動鏈剛度折算到末端的等效剛度；k1為驅動機構回轉彈簧的等效剛度，是彈簧機構彈簧剛度ks1折算到末端的等效剛度和驅動機構回轉結構剛度的綜合。

圖3 彈簧機構特性曲線Fig.3 Characteristic curve of spring mechanism

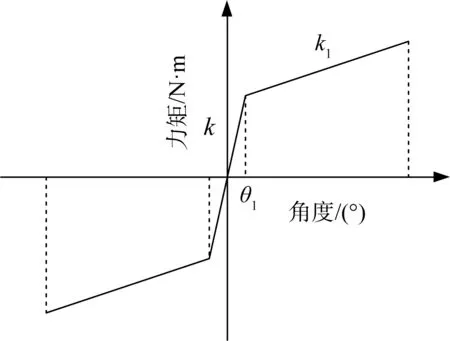
圖4 驅動機構等效剛度特性曲線Fig.4 Equivalent stiffness characteristic curve of driving mechanism

彈簧機構的彈簧剛度等效到驅動機構末端的剛度k1e為：

當k≥k1e時，有k1=k1e。

當外負載力矩小于驅動機構末端等效彈簧初始力矩時，k與傳動齒輪接觸剛度、軸的扭轉剛度相關。

2）等效阻尼系數。

定義阻尼器的等效阻尼系數為c，驅動機構的等效阻尼系數為B，根據傳動比關系，有：

k和B與制動過程的頻率、振幅密切相關，制動過程可以由阻尼自由振動模型描述。

若以制動的前一刻作為起始時刻（t=0 s），則在勻速平穩狀態下，關節扭角θ=0°，關節轉速θ˙=ω0，其中ω0為起始時刻驅動機構輸出角速度。

t=0 s時驅動機構在制動過程的運動特性可以簡化表示為：

已知要求ω0=0.14°/s，取k∈［100，1 500］Nm/°，根據式（6）和不同工況下驅動機構的等效阻尼系數（如表1所示）求解制動力矩和關節扭角，得到4組制動力矩—剛度和扭角—剛度特性曲線，如圖5所示。

表1 不同工況下驅動機構的等效阻尼系數Table 1 Equivalent damping coefficient of driving mechanism under different working conditions

圖5 制動力矩—剛度和扭角—剛度特性曲線Fig.5 Characteristic curves of brake torque-stiffness and torsion angle-stiffness

由圖5可知：當k＞210 Nm/°時，θ隨著k的增大而減小，T隨著k的增大而增大；當k＞400 Nm/°時，B對θ影響的敏感度明顯減小。

為了提高大慣量負載制動過程的穩定性，取θmax=1°，B=3 000 Nms/°，得到k=810 Nm/°。

1.2.3 傳動比分配

已知c=2×10-5Nms/°，確定i2·i3≈8 682。由前文分析確定i1·i2≈235 000。

彈簧機構初始力矩Ts0與驅動機構末端等效彈簧初始力矩T0的關系須滿足：

式中：η為彈簧機構到末端輸出的傳動效率，按照航天空間機構應用的經驗數據，在601EF真空油脂潤滑條件下，4級直齒傳動時取η=0.85；T0可以根據驅動機構回轉結構等效傳動剛度和制動扭角得到。

根據式（7），計算得到i2≥430.3。最終根據實際齒輪傳動參數設計得到傳動比分配如下：

電機到彈簧機構為5級直齒傳動和1級行星齒輪傳動，i1=535.33；

彈簧機構到末端輸出為3級直齒傳動和1級行星齒輪傳動，i2=439.75；

彈簧機構到阻尼器為3級直齒傳動，i3=19.75。

2 驅動機構動力學分析和驗證

2.1 驅動機構啟動和制動仿真分析

顯然，上述負載驅動機構的數學模型和參數計算忽略了傳動鏈空程、齒輪嚙合剛度和阻尼、傳動效率、系統摩擦阻尼、彈簧機構滯回等非線性特性。為了進一步驗證負載驅動機構的真實運動特性，須將上述非線性特性反映在仿真計算模型中，并將仿真結果與實驗結果進行比對和互驗。

1）傳動鏈空程。

負載驅動機構傳動鏈空程由齒輪傳動側隙引起。側隙Jt=φ·dP/2，式中：dp為節圓直徑，φ為轉角。為適應空間高低溫環境，采用中等齒輪側隙進行設計［20］。

2）齒輪嚙合剛度和阻尼。

全齒嚙合法向剛度kbn和嚙合阻尼系數bbn分別為：

式中：kLn為直齒傳動單對齒嚙合剛度；bω為齒寬；εγ為齒牙接觸比例。

為不失一般性，單對齒嚙合剛度取通用值。

3）傳動效率。

針對直齒傳動、錐齒輪傳動、行星傳動的傳動效率η1、η2、η3，須考慮軸承和聯軸環節的黏性摩擦阻尼。

4）系統摩擦阻尼。

為了便于與實驗結果進行比較，還應考慮系統摩擦力矩TF。其可通過實驗系統實測獲得。

5）彈簧機構滯回。

彈簧機構卷簧表面進行了MoS2黏結固體潤滑涂覆，通過實測可以得到常溫及高低溫下的摩擦力矩損失比例Tf/T。由于彈簧機構卷簧在上緊和釋放過程中的摩擦力矩方向相反，因此上緊和釋放時相差2倍的摩擦力矩。

仿真采用多學科領域系統動力學建模和仿真軟件Simulationx。仿真模型的非線性參數設置如表2所示。

表2 驅動機構動力學仿真模型的非線性參數Table 2 Nonlinearparameters ofdynamic simulation model of driving mechanism

按照傳動剛度模型、有/無彈簧機構緩沖和有/無阻尼器耗能等，將驅動機構仿真工況分為6種，如表3所示。

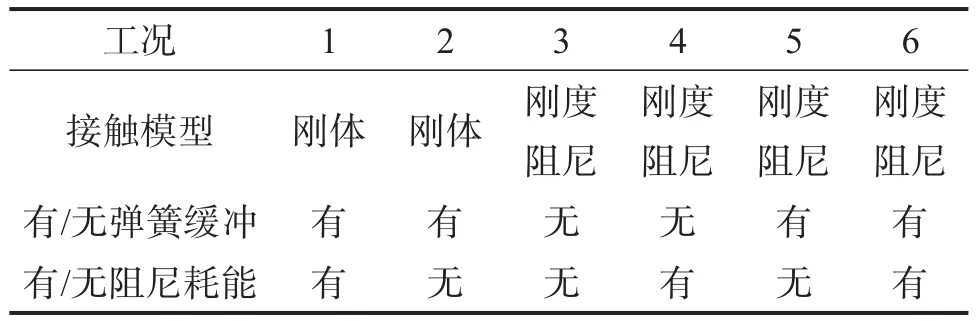
表3 驅動機構仿真工況Table 3 Simulation conditions of driving mechanism

仿真時長為1 000 s，轉角行程為117°，大慣量啟動和制動仿真結果如圖6所示。

圖6 大慣量啟動和制動仿真結果Fig.6 Simulation results of large inertia starting and braking

仿真結果表明：

1）結構剛度對驅動機構啟動和制動過程的平穩性具有顯著影響；

2）考慮結構剛度后，驅動機構在啟動和制動過程的力矩峰值均顯著下降；

3）增加緩沖阻尼后，驅動機構在啟動和制動過程的力矩峰值和速度穩定性均得到明顯改善。

2.2 彈簧阻尼特性測試

為了得到真實的驅動機構等效彈簧阻尼特性，通過反向加載的方法對驅動機構120°、240°兩個工作位置進行正反向彈簧阻尼特性測試，以獲得驅動機構實際的剛度和阻尼特性。加載速度為0.08°/s，測試得到驅動機構的力矩—角度、力矩—時間曲線，分別如圖7、圖8所示。

圖7 驅動機構的力矩—角度測試曲線Fig.7 Torque-angle test curve of driving mechanism

圖8 驅動機構的力矩—時間測試曲線Fig.8 Torque-time test curve of driving mechanism

由測試曲線可知：

1）由于機構傳動空程（約0.7°）的存在，2條曲線存在角度相位錯移，但測試結果基本一致；

2）正轉和反轉時的特性曲線具有良好的對稱性，說明機構正反向性能較一致；

3）上緊過程和回復過程具有較明顯的滯回特性，說明機構阻尼及摩擦耗能起到明顯作用。實際測得摩擦阻尼力矩平均為310 Nm。取末端到阻尼器7級齒輪傳動（1級行星、1級錐齒輪和5級直齒傳動）效率為0.8，算得阻尼系數為3 100 Nms/°，與1.2節中設計結果的誤差為3.3%。

4）結構等效剛度遠大于彈簧機構等效剛度，與圖4所示的驅動機構等效剛度特性相吻合。實際測得的結構等效剛度約為873 Nm/°，與1.2節中設計結果的誤差為7.8%。

通過以上分析可知，該驅動機構彈簧阻尼特性與理論設計相吻合，可用于大慣量啟動和制動實驗驗證。

3 大慣量啟動和制動實驗驗證

3.1 實驗目的

驗證驅動機構對大慣量負載的驅動能力及其運動平穩性和運動精度，以評價其在實際工程應用的可行性。

3.2 實驗方案

實驗在我國航天某型號專研的大慣量加載性能實驗系統上進行。大慣量加載性能實驗系統的組成如圖9所示，實物如圖10所示。

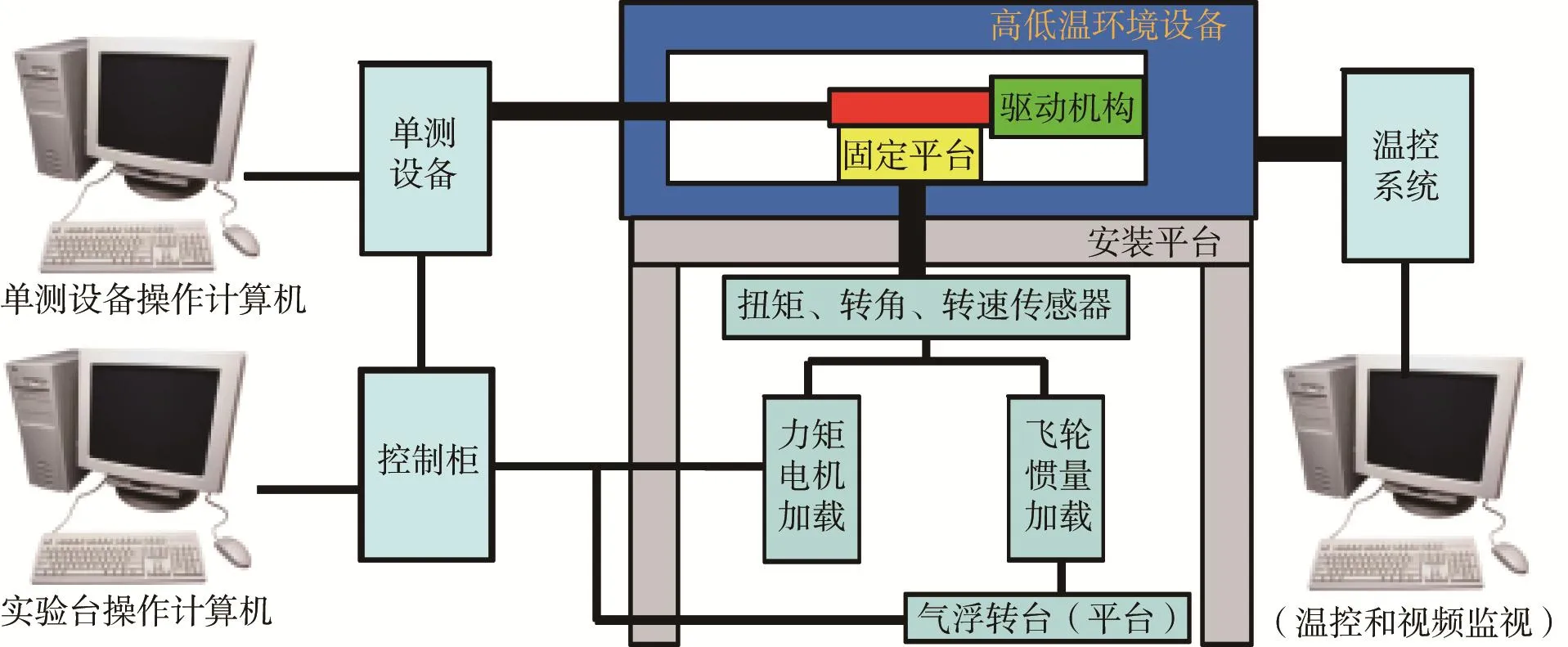
圖9 大慣量加載性能實驗系統的組成Fig.9 Composition of large inertia loading performance experimental system

圖10 大慣量加載性能實驗系統Fig.10 Large inertia loading performance experimental system

實驗系統采用大飛輪質量盤實現大慣量加載，飛輪與驅動機構之間設置了1∶6增速器，以減小對飛輪質量的需求；固定平臺用于驅動機構的安裝和固定；氣浮轉臺用于減小飛輪慣量加載系統自重引起的摩擦轉矩；扭矩、轉角、轉速傳感器分別用于測量關節的負載力矩、工作轉角和轉速；單測設備用于對驅動機構的驅動控制和信號采集；控制柜用于對實驗系統的控制和信號采集，并與單測設備進行驅動機構實驗狀態信息的交互；高低溫環境設備用于提供高低溫環境，并且具有照明和視頻監控功能；安裝平臺用于支撐負載模擬器和高低溫環境設備。

3.3 實驗結果及分析

實驗中轉動慣量為2.2×106kgm2，轉動角度為117°，從0°轉到117°，實驗結果如圖11所示。

圖11 大慣量啟動和制動實驗結果Fig.11 Test results of large inertia starting and braking

分析實驗結果可知：

1）在機構正轉和反轉過程中，啟動和制動力矩曲線、速度曲線均具有較高的重合度，且其峰值基本一致。

2）啟動和制動力矩峰值為400～500 Nm，遠小于驅動機構4 000 Nm的承載能力。

3）啟動速度峰值為0.221°/s，穩定速度為0.14°/s，超調量約為50%，與圖6（f）所示的仿真結果吻合。驅動機構輸出的絕對速度較低，運行平穩。

4）制動過程持續1.5個振蕩周期，運行3 min后驅動機構趨于停轉，與圖6（f）所示的仿真結果一致。角度的精度優于1°，包括了驅動機構自身空程角度，可見機構的運動精度滿足工程應用要求。

5）根據表2所示的動力學參數算得最大啟動力矩為320 Nm，最大制動力矩為580 Nm。最大啟動力矩理論值比實驗值小，最大制動力矩理論值比實驗值大。顯然，實驗中聯軸工裝、飛輪慣量支撐軸承和增速器等同樣起到了一定的緩沖效果。

6）根據式（6）算得的在制動過程中最大扭角為0.85°，考慮在制動過程中機構傳動效率仍按0.8計算，得到制動過程的最大扭角為0.68°，與圖11（f）所示的實驗值（0.65°）的誤差為4.4%，說明計算結果基本與實驗結果吻合。

綜上，通過在工況6下的實驗結果與仿真結果的對比可知，振蕩周期、啟動時間、啟動速度超調量和制動時間等曲線形態特征較一致。此外，由于實驗中聯軸工裝和大質量飛輪慣量連接軸剛度和阻尼的影響，啟動和制動力矩峰值、制動速度超調量的實驗值較仿真值小，并使得在轉速平穩工作段存在力矩和速度的小幅波動。

4 結論

設計了以小功率驅動大慣量負載的驅動系統，其已成功應用于我國空間站轉位機械臂中。建立了具有多級齒輪傳動、彈簧緩沖、阻尼耗能及電磁制動等功能的驅動機構，其能較好地實現大負載慣量的平穩啟動、制動和停止時的精準定位。

實驗結果表明，提高傳動比可以降低電機端等效負載慣量，減小輸出端負載變化引起的力矩波動。而大減速比傳動帶來的驅動輸出效率的降低對低速大負載轉動慣量驅動的影響并不顯著。

雖然實驗中驅動機構和試驗工裝結構剛度的影響無法解耦，但通過對在一定范圍內等效剛度和等效阻尼的影響分析，表明該驅動系統可以滿足工程應用的要求。