一體化磁梯度系統誤差補償算法

馬劍飛，丁 凱，顏 冰，林春生

（1. 海軍工程大學 兵器工程學院，湖北 武漢 430033；2. 近地面探測技術重點實驗室，江蘇 無錫 214035）

0 引言

磁異常探測技術具有不受空氣、海水、泥沙、土壤等介質影響的優勢，在勘探礦物、航空反潛以及未爆彈（unexploded ordnance，UXO）探測等方面具有廣泛而深入的應用，其作為一種被動探測技術具有隱蔽性好的特點[1-3]。隨著超導磁力儀技術的發展，基于矢量磁梯度的磁異常探測愈發受到重視[4-5]。矢量磁梯度相對磁標量探測以及磁矢量探測的優勢在于：1）測量結果與地磁傾角和地磁偏角無關；2）具有更豐富的磁場信息，可以利用幾個測量點的磁梯度張量快速反演目標的位置和磁矩[6]；3）具備很強的共模抑制能力，特別是當測量平臺晃動時，測量值可以有效避免地磁場和背景磁場噪聲影響[7]。

然而，磁梯度測量系統對傳感器的一致性、測量精度以及裝配技術都有很高的要求，其誤差主要包括磁通門傳感器本身的測量誤差和系統各傳感器之間的非對準誤差。三分量磁通門傳感器測量誤差主要包含各軸之間不嚴格正交引起的非正交誤差，各軸電氣性能不一致所引起的靈敏度誤差以及各軸零點偏移所引起的零偏誤差；傳感器之間的非對準誤差是指受安裝時工藝所限，安裝后各磁通門傳感器的三軸指向不能嚴格保持一致，受地磁場的影響而導致系統本身就存在較大的梯度差。

張光等研究了利用標量磁傳感器補償三分量磁傳感器測量誤差的方法[8]，林春生等提出了一種不依賴于標量磁傳感器的旋轉補償測量誤差的方法[9]，上述2種方式在參數建模時忽略了變量轉換過程中的高階小量，李青竹等據此提出了一種考慮高階小量的測量誤差補償方式[10]，并取得了更好的補償結果。

在對準誤差補償方面，一般的方式是選用磁梯度張量系統中的一個磁力儀作為參考去補償其它傳感器的非對準誤差[11-13]，這種補償方式導致張量系統輸出參考方向與運動平臺正交坐標系的方向不是嚴格一致。李青竹等以補償后的多個傳感器的平均指向作為參考補償磁梯度張量系統的非對準誤差[10]，這種補償方式使得系統輸出參考方向更加接近于運動平臺正交坐標系方向。

載體平臺在運動過程中，由于自身材料磁化和切割地磁場，會產生干擾磁場，如載體固有磁場、感應磁場和渦流磁場等，鑒于水下運動平臺的運動速度和加速度很小，故不考慮渦流磁場。文獻[14]以理想磁梯度張量矩陣為對稱性矩陣以及矩陣的跡為0的特性作為適應度函數，利用遺傳算法對補償參數進行尋優解算，取得了較好的平臺干擾誤差補償結果。

現有的誤差補償方法是分別對每個磁傳感器的測量誤差、磁傳感器之間的對準誤差以及運動平臺產生干擾磁場進行補償，但是系統在長時間的工作后，標定參數必然發生變化，對于成熟裝備如果要拆開裝備并重新逐步校正必然浪費極大的人力物力，本文旨在提出一種簡便可行的一體化磁梯度張量系統誤差補償方案。

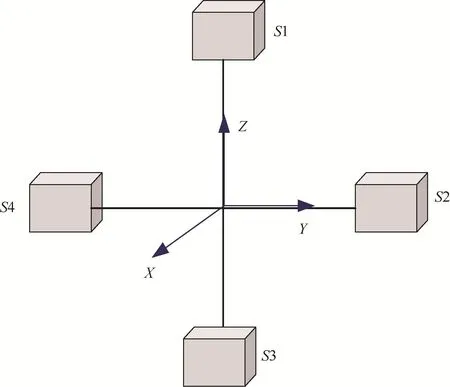
圖1 十字形磁梯度張量系統Fig.1 Cross shaped magnetic gradient tensor system

1 磁梯度誤差校正模型

當探測距離大于2.5倍磁性目標長度時，磁性目標可以視為一個磁偶極子[15]，此時距離磁性目標r處的磁場矢量可以表示為

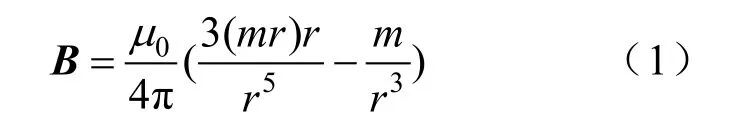
式中：0μ為空間磁導率，對B的三分量分別在x、y和z 3個方向求偏導，可得到磁梯度張量G為

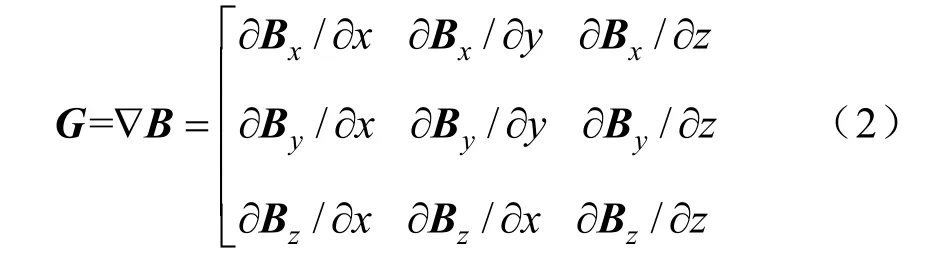
對于十字形的磁梯度張量系統，一般采用傳感器短距離基線的矢量讀數差近似代替磁標勢二次偏微分：

受載體磁環境以及磁傳感器工藝的影響，水下運動平臺的磁梯度張量系統主要誤差來源包括：

1）載體磁干擾：載體平臺在運動過程中會產生干擾磁場，如載體固有磁場、感應磁場和渦流磁場等，由于水下運動平臺的運動速度和加速度很小，故不考慮渦流磁場。固有磁場源于載體自身以及所安裝設備的硬磁性材料的剩磁，由于硬磁材料具有較高的矯頑力，所以固有磁場一般不隨載體運動而發生變化，一般假設這部分磁場在載體坐標系內的投影是恒定的，記為bh；感應磁場主要源于自身軟磁性材料在地磁場中磁化所產生的磁場，軟磁材料具有較低的矯頑力，當外磁場Ba的相對方向變化時，感應磁場也隨之變化，一般假設其與載體坐標系方向測量呈線性關系，因此載體磁干擾滿足

式中：Cs為軟磁感應系數矩陣，一般假設其為實對稱矩陣。

2）非對準誤差：傳感器坐標系與載體坐標系的指向偏差

式中，

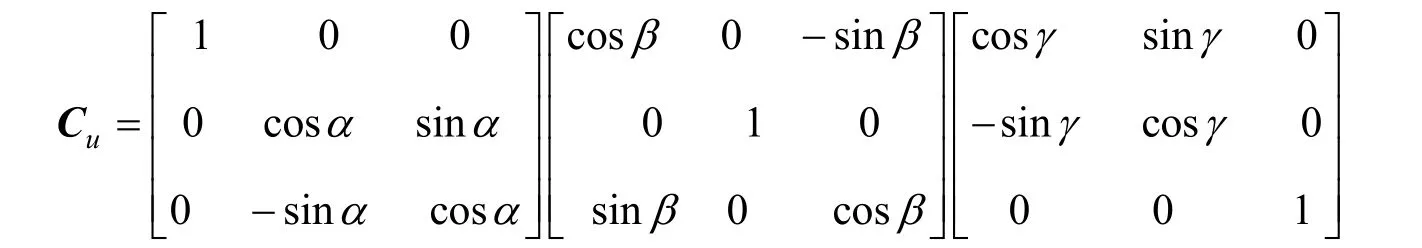
式中，α、β、γ分別表示傳感器坐標系與載體坐標系之間的橫滾角、俯仰角和方位角。

3）傳感器誤差：設傳感器坐標系為 OXYZ，理想的正交坐標系為 OX′Y′Z′，傳感器誤差主要包括非正交誤差、比例誤差以及零點漂移

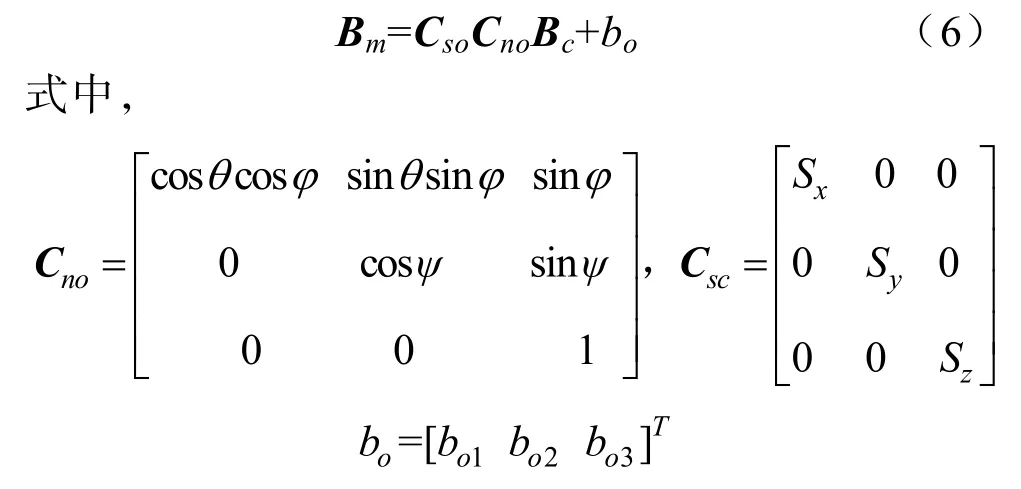
式中：Y軸與Y′的夾角為ψ，X′軸與XOY平面的夾角為φ，X′軸在 XOY平面的投影與 X軸的夾角為θ，sx、sy與 sz分別為磁傳感器 X′軸、Y′軸和 Z′軸的靈敏度，bo1、bo2與 bo3分別為 X軸、Y軸和 Z軸的零點漂移。

結合載體磁干擾、非對準誤差以及傳感器誤差，單個磁傳感器的誤差綜合模型為

式中：Bmj表示4個傳感器第j測量的平均值，故可以用Bmj替代式（11）中的Baj。要求解標定參數 K24就必須使得 Bd行滿秩，即需要至少構建 4組滿足互不線性相關條件的測量方程，此時式（12）的最小二乘解為

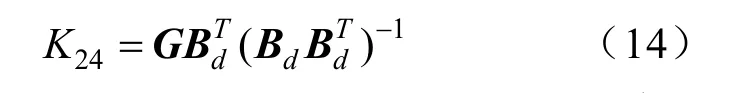
顯然，從式（14）的K24中可以獲取標定參數（C2–C4）和標定參數（b2–b4），同理也可以得到標定參數（C1–C3）以及（b1–b3）。雖然此校正算法不能顯式求解 Cs、Cu以及 Cno等參數，但｛C1- C3, C2- C4, b1- b3, b2-b4｝這些等效標定參數代入式（10）就足以對十字形磁梯度張量系統進行校正。

2 磁梯度誤差校正實驗

2.1 解算標定參數

為驗證校正算法的性能，根據式（7）的測量模型，設水下運動平臺的十字形磁梯度系統中4個磁傳感器所在位置的軟磁感應系數分別為

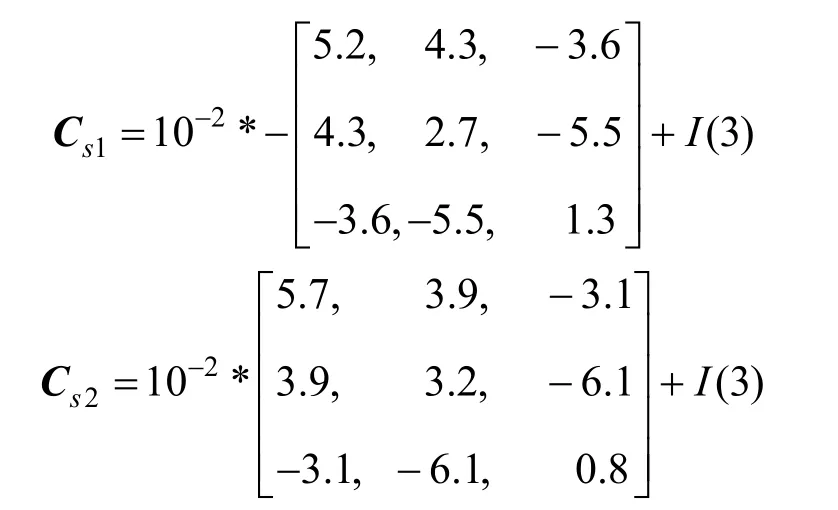
設水下運動平臺的十字形磁梯度系統中4個磁傳感器所在位置的固有磁場分別為

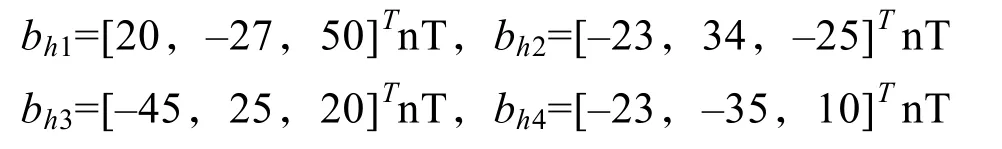
設4個磁傳感器坐標系與載體坐標系指向偏差的橫滾角、俯仰角和方位角組成的向量[α，β，γ]分別為[0.01π，–0.02π，0.03π]、[–0.03π，0.01π，0.04π]、[0.02π，0.02π，–0.01π]以及[–0.01π，0.03π，–0.02π]；4 個磁傳感器的靈敏度[Sx，Sy，Sz]分別為[0.998,1.003,1.002]、[0.999,1.007,1.005]、[1.003，1.001，0.999]以及[1.002,0.995,0.998]；4 個磁傳感器的非正交角[θ，φ，ψ]分別為[0.02π，–0.01π，–0.02π]、[0.01π，0.01π，0.05π]、[0.05π，0.03π，0.01π]以及[–0.03π，–0.03π，0.02π]；4 個磁傳感器的零點漂移分別為

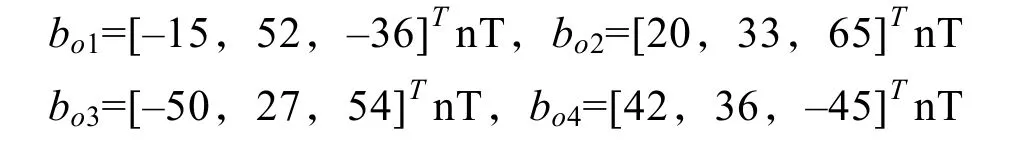
設地球磁場的模值為50 μT，地磁偏角為π/4，地磁傾角為π/3，磁梯度系統誤差校正選取的m組姿態角進行校正，由式（14）所解算的標定參數為

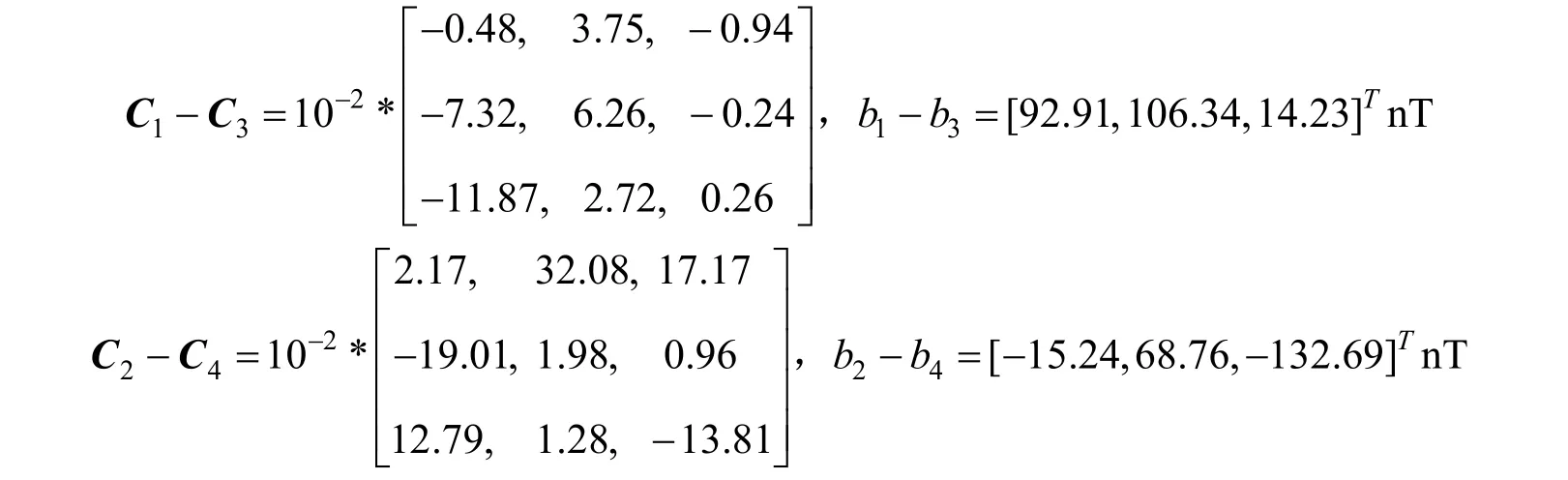
如圖2所示，淺色線條表示十字形磁梯度張量系統在1 000個姿態條件下校正前的輸出結果，深色線條表示一體化校正方法校正后的結果，通過對比可以發現，受載體磁干擾、非對準誤差以及傳感器誤差的影響，校正前的磁梯度輸出甚至可達2 μT/m，而校正后的磁梯度輸出小于0.1 nT/m。上述結果表明：本文提出的一體化校正算法雖然不能顯示求解一些標定參數，但可以通過少數幾個點的測量值對磁梯度張量系統的輸出進行有效校正，而且校正過程簡便易行，不需要額外的先驗磁場信息。

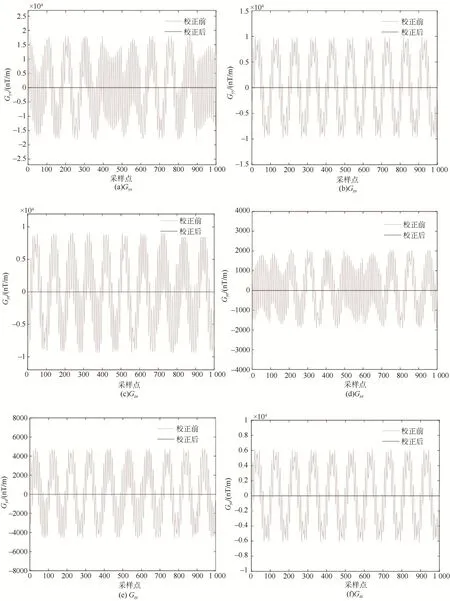
圖2 磁梯度張量校正結果Fig.2 Calibration results of magnetic gradient tensor

2.2 磁梯度張量校正

前一節檢驗了沒有磁性目標時一體化校正算法校正磁梯度信號的能力，本節旨在通過仿真實驗檢驗一體化校正算法校正磁梯度信號的能力。磁梯度張量測量系統固定在載體平臺上，X軸與運動平臺的軸線重合并指向運動平臺的艏部，Y軸指向左舷，Z軸豎直向上。仿真條件設置為：磁梯度張量測量系統基線L為0.5 m；采樣頻率fs為5 Hz；磁性目標磁矩 m為(–3，1，5)×103A·m2；初始時刻目標的位置為（–100，30，5）m；運動平臺 X方向運動速度VX為5 m/s；地磁場矢量Bs為（17.69，30.62，35.36）μT；水下運動平臺的十字形磁梯度系統中4個磁傳感器所在位置的軟磁感應系數、硬磁偏置等參數與2.1節一致。

如圖3所示，其中真實值表示理想十字形磁梯度系統測量的信號，測量值表示實際十字形磁梯度系統測量且經過去偏置處理之后的信號，校正值表示測量值經過一體化校正算法處理之后的結果。通過與磁梯度信號真實值對比可以看出，磁梯度信號測量值發生了嚴重的畸變，這種畸變會嚴重影響磁梯度的定位和跟蹤精度。表1分別計算了一體化校正前后的磁梯度信號各分量誤差，校正后誤差降低到校正前誤差的8%以下，這說明一體化校正算法能夠有效克服實際磁梯度系統測量信號畸變所帶來的不利影響。

表1 磁梯度張量校正誤差Table 1 Calibration errors of magnetic gradient tensor

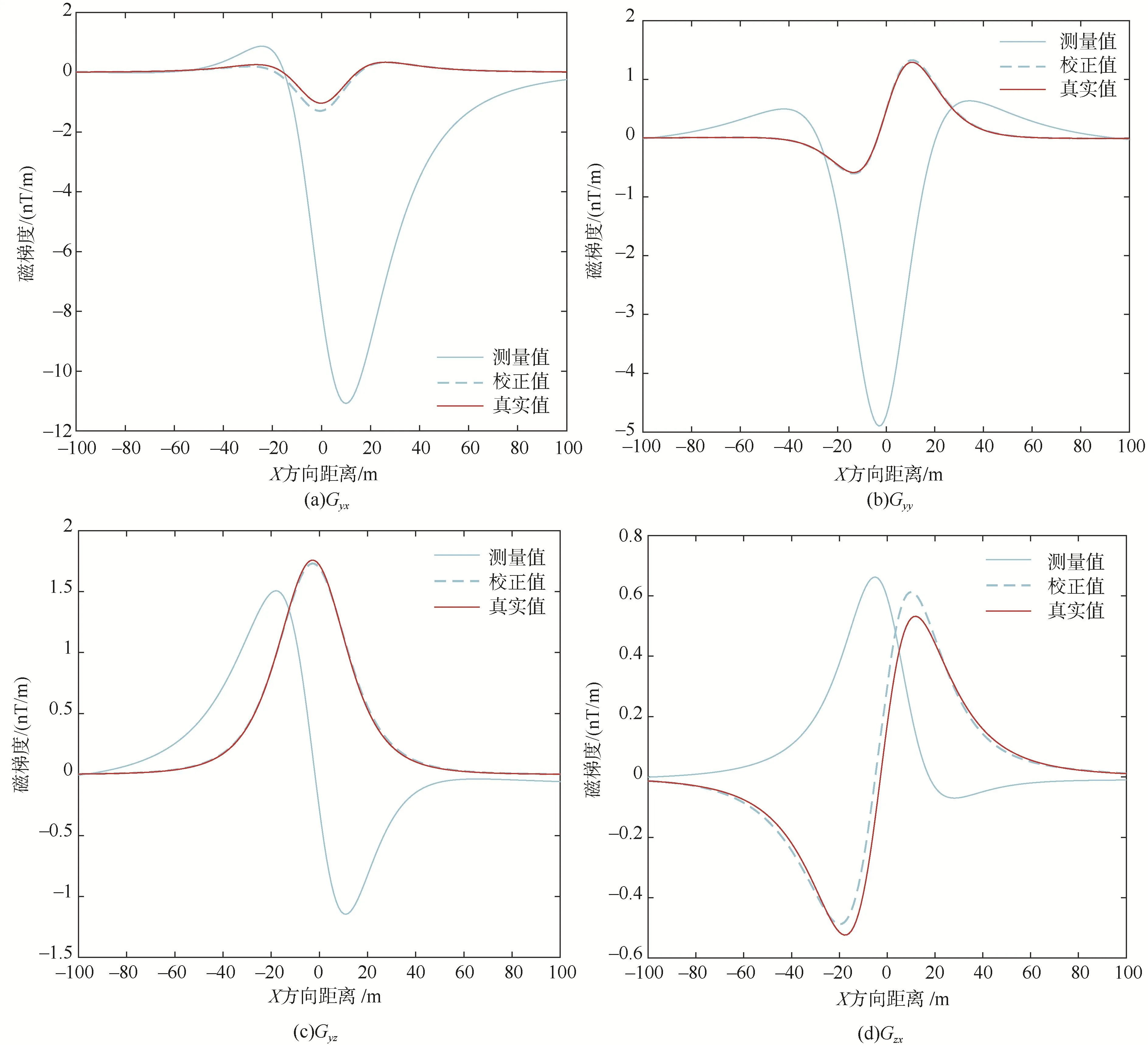
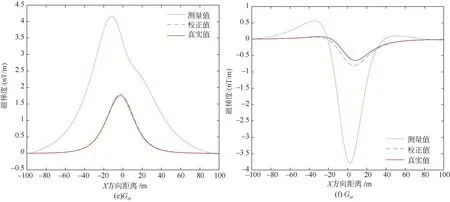
圖3 磁梯度張量校正結果Fig.3 Calibration results of magnetic gradient tensor

2.3 磁梯度誤差校正試驗

為驗證一體化磁梯度誤差校正算法的性能，校正試驗的測量點位于午夜時分的消磁實驗室，如圖4所示，磁梯度測量系統為4個傳感器呈十字形布置的Mag–03磁通門傳感器，布置在十字形亞克力板的凹槽內。采集設備為 NI USB–6216采集卡，NI USB–6216是一款具備16路模擬輸入端或8個差分輸入端，16位ADC分辨率，最大采樣頻率為250 kS/s的多功能AD數據采集設備。

圖4 磁梯度張量測量試驗Fig.4 Magnetic gradient tensor measurement test

由于3號傳感器的測量出現了錯誤，這里僅對2號和4號組成的磁梯度儀進行誤差校正，如圖5所示，是磁梯度系統在不同姿態下的校正輸出。淺色線條表示未校正前測量度測量結果，深色線條表示一體化校正方法校正后的結果，通過對比可以發現，受載體磁干擾、非對準誤差以及傳感器誤差的影響，校正前的磁梯度輸出甚至可達5 μT/m，而校正后的磁梯度輸出小于100 nT/m，表明一體化校正算法可以很大程度上降低測量誤差。

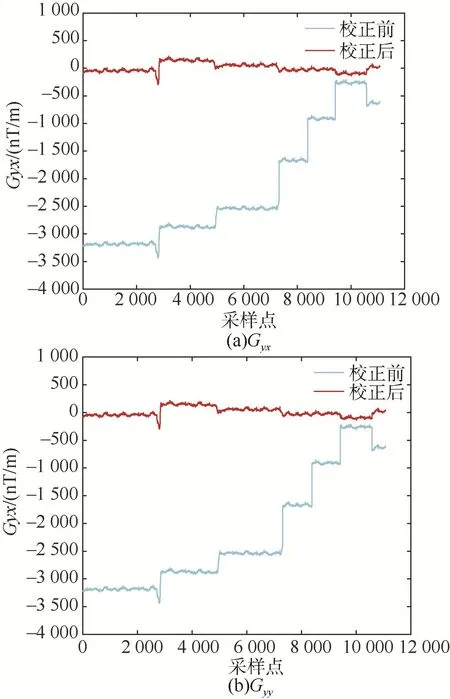
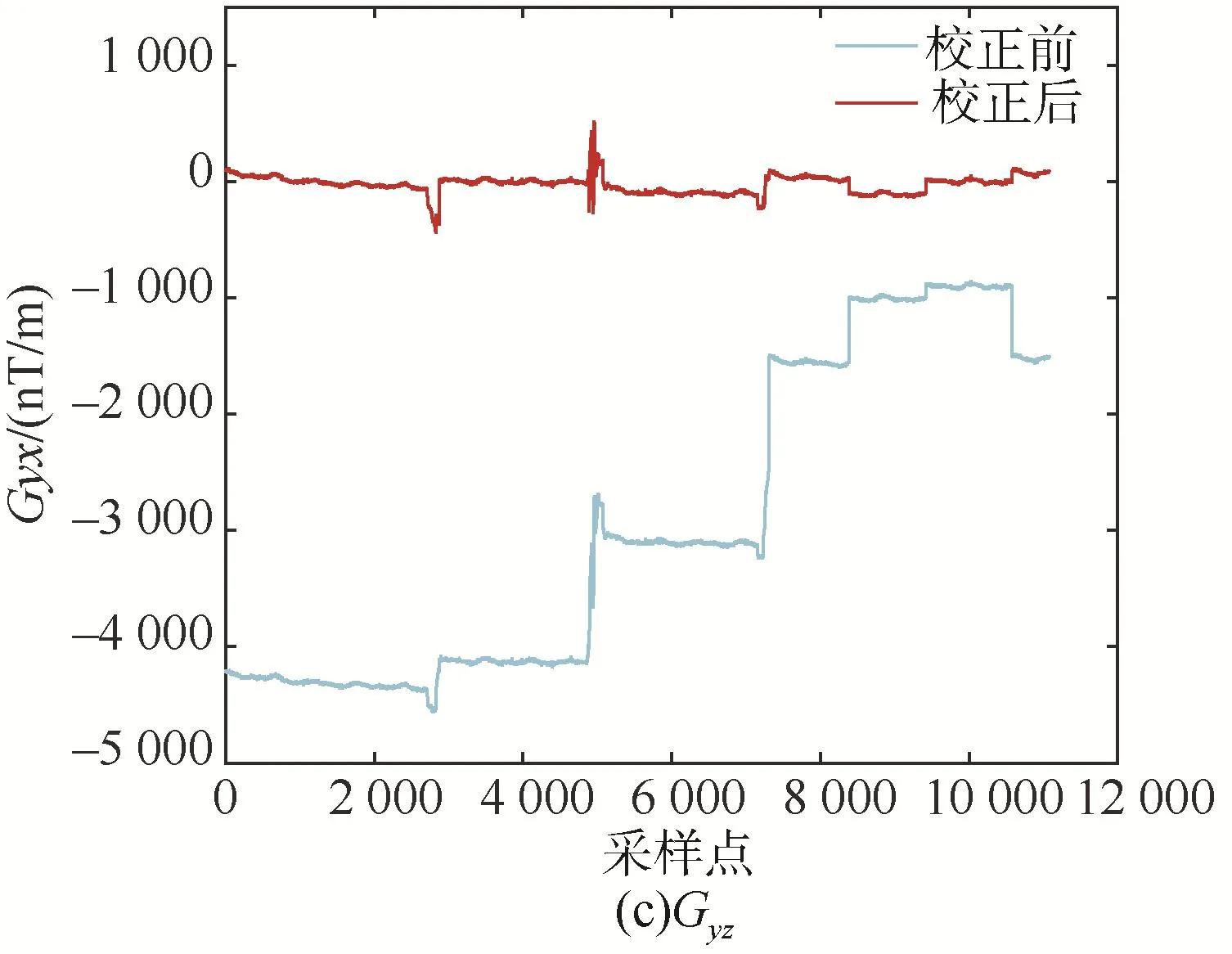
圖5 磁梯度校正結果Fig.5 Calibration results of magnetic gradient

3 結束語

梯度測量系統對傳感器的一致性、測量精度、以及裝配技術都有很高的要求，現有的誤差補償方法在磁梯度張量誤差過程中，分別對磁力儀的測量誤差、磁力儀之間的對準誤差以及運動平臺產生干擾磁場進行補償，但是系統在長時間的工作后，標定參數必然發生變化，對于成熟裝備拆開裝備并重新逐步校正必然浪費極大的人力物力。本文提出了一種簡便可行的一體化磁梯度張量系統誤差補償算法，仿真結果表明：對于十字形磁梯度張量測量系統，校正后誤差降低到校正前誤差的8%以下，實測數據校正結果表明：校正前的磁梯度輸出甚至可達 5 μT/m，而校正后的磁梯度輸出小于 100 nT/m，表明一體化校正算法可以有效克服磁梯度系統測量信號畸變所帶來的不利影響。