阻尼板振動復模態可控性和可觀性研究

劉江， 黎勝

(1.大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連 116024； 2.大連理工大學 船舶工程學院，遼寧 大連 116024)

振動主動控制是振動工程研究領域中的熱點之一，其工作原理是通過自動修改結構響應來減小結構的振動。振動主動控制系統的形式多種多樣，但是任何此類系統都包含傳感器、控制器和作動器[1]，顯然，傳感器和作動器的布置關系到振動主動控制系統的控制效果，應盡量避免布置在結構振動不可控和不可觀位置。結構振動模態的可控性和可觀性定義為：安裝在振動結構上的作動器能夠激起結構的所有模態則此振動結構是可控的；安裝在振動結構上的傳感器能夠檢測到結構的所有模態則此振動結構是可觀測的[2]。因此，結構振動的可控性和可觀性對振動主動控制系統傳感器/作動器的布置具有重要意義。

目前對結構振動主動控制中可控性和可觀性問題的研究有：Balas等[3]研究了無阻尼和輕阻尼柔性結構的可控性和可觀性。Wu等[4]指出，對于柔性結構，傳感器和作動器的配置與可控性和可觀性有關。黎勝等[5]對結構振動和聲輻射可控性和可觀性指標進行了研究，提出了基于聲壓輸出的振動模態可觀性指標，并且在振動模態可控性和可觀性基礎上，結合振動模態的聲輻射效率，提出了結構聲輻射的可控性和可觀性指標和基于聲壓輸出的可觀性指標。但是，上述研究都是基于實模態展開的，而且對于實模態來說，各階振動模態節點位置都是該階模態不可控和不可觀位置。而實際的結構振動不可避免的會受到阻尼或者流體加載等因素的影響，都是以復模態的形式存在[6]。

復模態與實模態的區別主要在于：1) 復模態不存在各點位移均為零的瞬間；2) 各點位移之間的比值隨時間變化；3) 一般不具有實模態振型所具有的那種穩定的節點或節線[7]。這就導致在可控性和可觀性研究時，基于實模態理論的分析就會與結構的實際可控性和可觀性產生偏差，從而導致主動控制系統的控制效果減弱。因此基于復模態的阻尼板可控性和可觀性研究具有重要的意義。目前可用于結構振動復模態可控性和可觀性的研究有：Hamdan等[8]提出了一階阻尼振動系統(控制方程)的可控性和可觀性指標，并且證明了所提出的指標可以直接應用于二階阻尼振動系統(阻尼系統運動方程)。Yang[9]研究了具有阻尼、陀螺和循環力共同作用的一般機械結構的可控性和可觀性，利用與運動方程相關的非正交特征向量來表示系統的傳遞函數，通過研究傳遞函數的行和列的線性無關性，得到了模態可控性和可觀性條件。

本文對文獻[8]提出的可控性和可觀性指標進行探討，論證了其用于復模態的可控性和可觀性分析的可行性。基于實模態和復模態理論，以阻尼板結構為例對其模態可控性和可觀性指標進行了計算分析，研究了復模態與實模態可控性和可觀性的差別。對不同構型阻尼板的復模態復雜度進行計算并探討了復雜度與復模態可控性和可觀性指標的關系，從可控性和可觀性角度闡釋了實模態和復模態的區別。

1 復模態可控性(可觀性)指標

振動控制理論中控制方程常表示為：

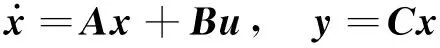
(1)

式中：A、B、C分別被稱作系統矩陣、輸入矩陣、輸出矩陣;x為系統響應向量(位移、速度等)；u為外部激勵力向量。為了方便描述，上述矩陣設置為：A2n×2n,B2n×m，Cm×2n,um×1。

基于式(1)的控制方程及其特征值問題的求解結果，對系統的可控性和可觀性，Kailath等[10]提出了著名的PBH檢驗準則，準則有PBH特征向量檢驗和PBH秩檢驗2種表示方式。Hamdan等[8]將PBH檢驗推廣到了二階振動方程情況，并基于PBH特征向量檢驗提出了可控性和可觀性指標。

振動方程與式(1)所示的控制方程是同一方程的不同形式，二階振動方程常表示為：

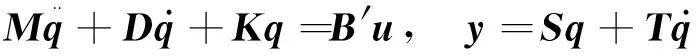
(2)

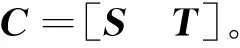
1) 在j階控制力情況下，i階模態是不可控的充分必要條件是：

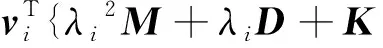
(3)

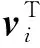
2) 在k階測量輸出情況下，l階模態是不可觀的充分必要條件是：

(4)

式中wl為第l個特征值對應的右特征向量；sk、tk分別為輸出矩陣S、T的第k列。基于上述特征向量檢驗，文獻[8]給出了二階振動方程的可控性和可觀性指標：

(5)

式中：θij為控制力位置向量b′j和左特征向量vi夾角；φkl為輸出位置向量sk+λltk和右特征向量wl夾角。可控性或可觀性越好上述指標值越大，指標為0的位置不可控或不可觀。

當上述指標用在振動實模態的可控性和可觀性研究時，各階振動模態的節點位置指標值恒為0，也就是說在振動實模態的可控性和可觀性研究中，節點位置是完全不可控和不可觀的位置。而振動復模態相比于實模態不存在固定節點，由此推測復模態的可控性和可觀性與實模態可能存在明顯的區別。通過上述分析可知，式(5)的可控性和可觀性指標是由式(2)所示的振動方程的特征向量與輸入輸出矩陣列向量的夾角表示，而且，式(2)包含阻尼矩陣信息，即其振動模態求解結果為復模態。所以本文認為，式(5)所示的可控性和可觀性指標可以用于振動復模態可控性和可觀性分析。

2 復模態對可控性和可觀性的影響

2.1 實模態和復模態結構模型

為了得到實模態和復模態，建立了如圖1(a)所示的均勻阻尼板和圖1(b)所示的非均勻阻尼板有限元模型：板長Lx=0.455 m，板寬Ly=0.379 m，板厚h=0.003 m，板密度ρ=7 850 kg/m3，楊氏模量E=2.1×1011N/m2，泊松比υ=0.3，邊界條件是四邊簡支。Rayleigh阻尼模型被廣泛用于商業有限元軟件中的阻尼結構的模態分析，且本文結果與阻尼模型無關，因此用該模型定義結構的阻尼。

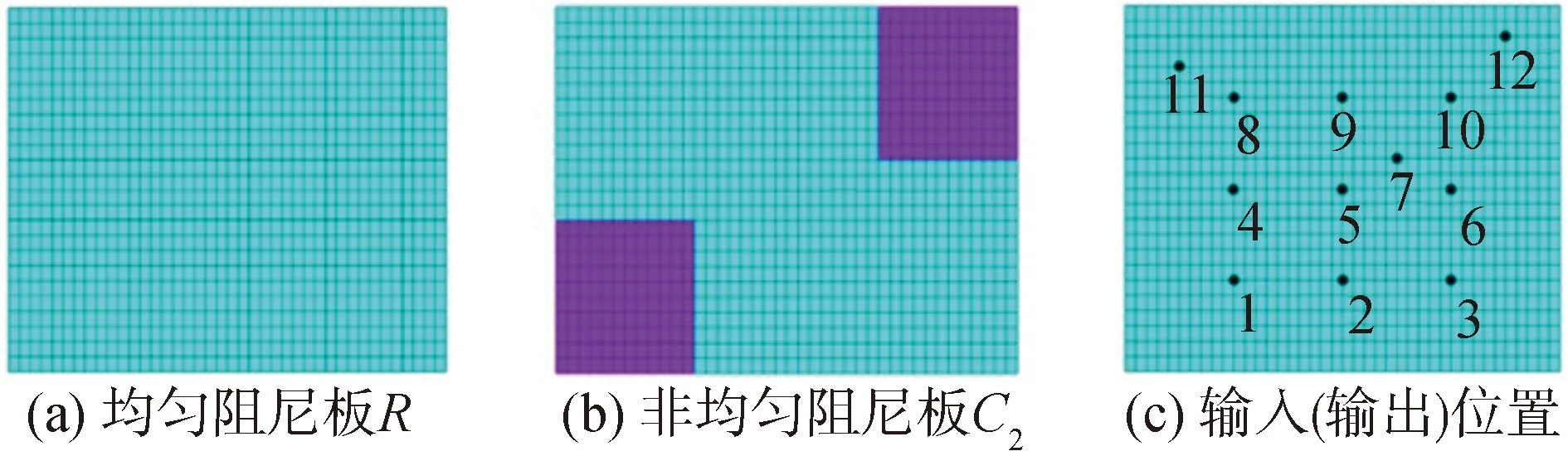
圖1 阻尼板有限元模型及輸入(輸出)位置Fig.1 FE-model of damped plates and positions of input (output)

對于非均勻阻尼板，通過在不同區域設置不同阻尼比來建立，淺色和深色區域阻尼比分別為ξ1和ξ2。阻尼矩陣D表示為質量矩陣M和剛度矩陣K的線性組合。在結構不同區域設置不同的阻尼比，其阻尼矩陣可以表示為：

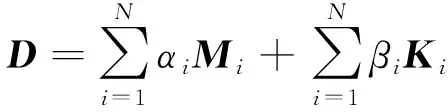
(6)

式中：N為阻尼區域的數量；Mi和Ki為第i個區域結構的質量陣和剛度陣；αi和βi為第i個區域的Rayleigh阻尼比例系數。假定第i個區域的期望阻尼比值為ξi，則比例系數可表示為：

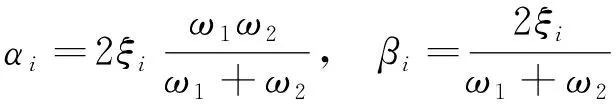
(7)

式中ω1和ω2為結構任意兩階固有頻率。

在上述有限元模型中，淺色區域代表純鋼板部分，ξ1=0.01，深色區域代表高阻尼部分，ξ2=0.2。模型網格劃分采用ANSYS?SHELL181單元，有限元網格為40×24，共有960個單元，1 025個節點[13]。利用DAMP模態求解器對均勻阻尼板R和非均勻阻尼板C2進行模態分析，得到其前五階振動模態，模態階數表示為a×b，a和b分別表示板長和板寬方向的波數。圖2給出了R板和C2板2×2和3×1階振動模態幅值和相位分布。

從圖中可以看出，由于阻尼的非均勻設置，結構的模態振型發生改變，尤其是相位的改變尤為突出，這也是復模態相較于實模態顯著的特點，結構的各個位置不再同時達到最大值、最小值或同時經過平衡位置。

2.2 實模態與復模態可控性(可觀性)對比

選取圖1(c)中所示的12個點作為板上用于輸入(主動控制的控制力)和輸出(振動響應測量)的位置，將實模態(R)和復模態(C2)的模態分析結果代入式(5)，分別計算其在12個點上前5階模態的模態可控性(可觀性)指標。圖3給出了實模態和復模態可控性(可觀性)對比結果，實線圖標代表實模態，虛線圖標代表復模態。需要說明的是圖3中的可觀性指標計算只考慮了振動位移測量輸出，對同一位置其模態可觀性和可控性指標是一樣的，即cosθ=cosφ。

從圖3中可以看出，對于實模態：位置1-12對1×1和3×1階模態都具有較好的可控性(可觀性)，位置2、5和9對2×1階模態是不可控(不可觀)的，位置4、5和6對1×2模態是不可控(不可觀)的，位置2、4、5、6和9對2×2階模態是不可控(不可觀)的；復模態與實模態有所不同：對于1×1，2×1，1×2階模態，復模態可控性和可觀性指標與實模態基本相同；對于2×2，3×1階模態，復模態可控性和可觀性指標與實模態明顯不同，且對于不同位置指標值有的增大有的減小。

綜上所述，在相同階模態和相同輸入(輸出)位置，實模態情況下的與復模態情況下模態可控性(可觀性)不同。

3 復雜度對可控性和可觀性的影響

3.1 復模態復雜度計算

目前常用的量化模態復雜度的參數有平均相位偏差MPD，模態相關系數MCC，模態相位共線性系數MPC，模態復雜度因子MCF(MCF1、MCF2、MCF3)，模態復雜度指標MSC[14]。本文主要通過模態分析得到阻尼板的振型數據進行計算分析，而MPD是由復振型的幅值和相位來量化模態復雜度的參數，因此選取MPD來量化不同構型板結構的模態復雜度。平均相位偏差(mean phase deviation，MPD)常表示為：

(8)

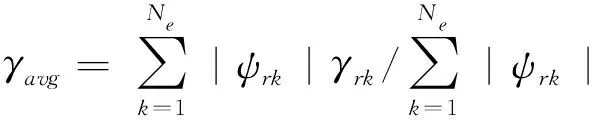
非均勻阻尼板高阻尼區域的分布情況會影響復模態的復雜程度，本文參考文獻[15]中定義的阻尼構型，根據對稱性和幾何分布的不同，構建圖4所示的8種構型。其中，S為對稱型，B為左右對稱型，C為中心對稱型，A為不對稱型，1、2是根據距離板中心和邊界的距離分別代表集中分散。有限元模型設置與2.1節一致，對8種不同構型的非均勻阻尼板進行模態分析，并代入式(8)計算其MPD值，計算結果如表1所示。

圖4 8種阻尼板構型Fig.4 8 configurations of damped plates

從表1可以看出，在 2×2和3×1階模態C2的復模態復雜度較高，在1×1、2×1和1×2階模態C2的復模態復雜度較低。結合圖3可以看出，在2×2和3×1階模態C2與R的可控性和可觀性指標存在明顯差異，在1×1、2×1和1×2階模態C2與R的可控性和可觀性指標基本相同。由此可知，在模態可控性和可觀性方面復模態相比于實模態的變化量與復模態復雜度有關。

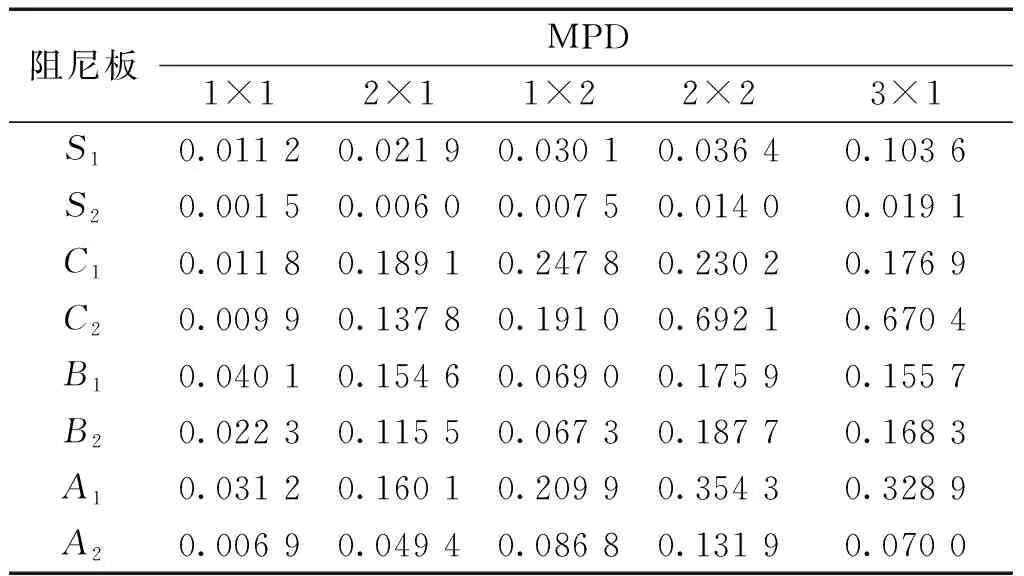
表1 8種阻尼板前5階MPD值Table 1 MPDs for 8 damped plates from 1st to 5th mode

3.2 可控性(可觀性)計算對比

為了研究模態復雜度對復模態可控性(可觀性)的影響，將8種阻尼板的前5階模態的可控性(可觀性)指標，分別按照MPD由小到大的順序重新整理，圖5～9分別為前5階模態不同構型的非均勻阻尼板(不同復雜度)，12個輸入(輸出)位置處的可控性(可觀性)指標與均勻阻尼板R的對比結果，其中，括號內的數字代表該構型在這階模態下的復雜度MPD值。

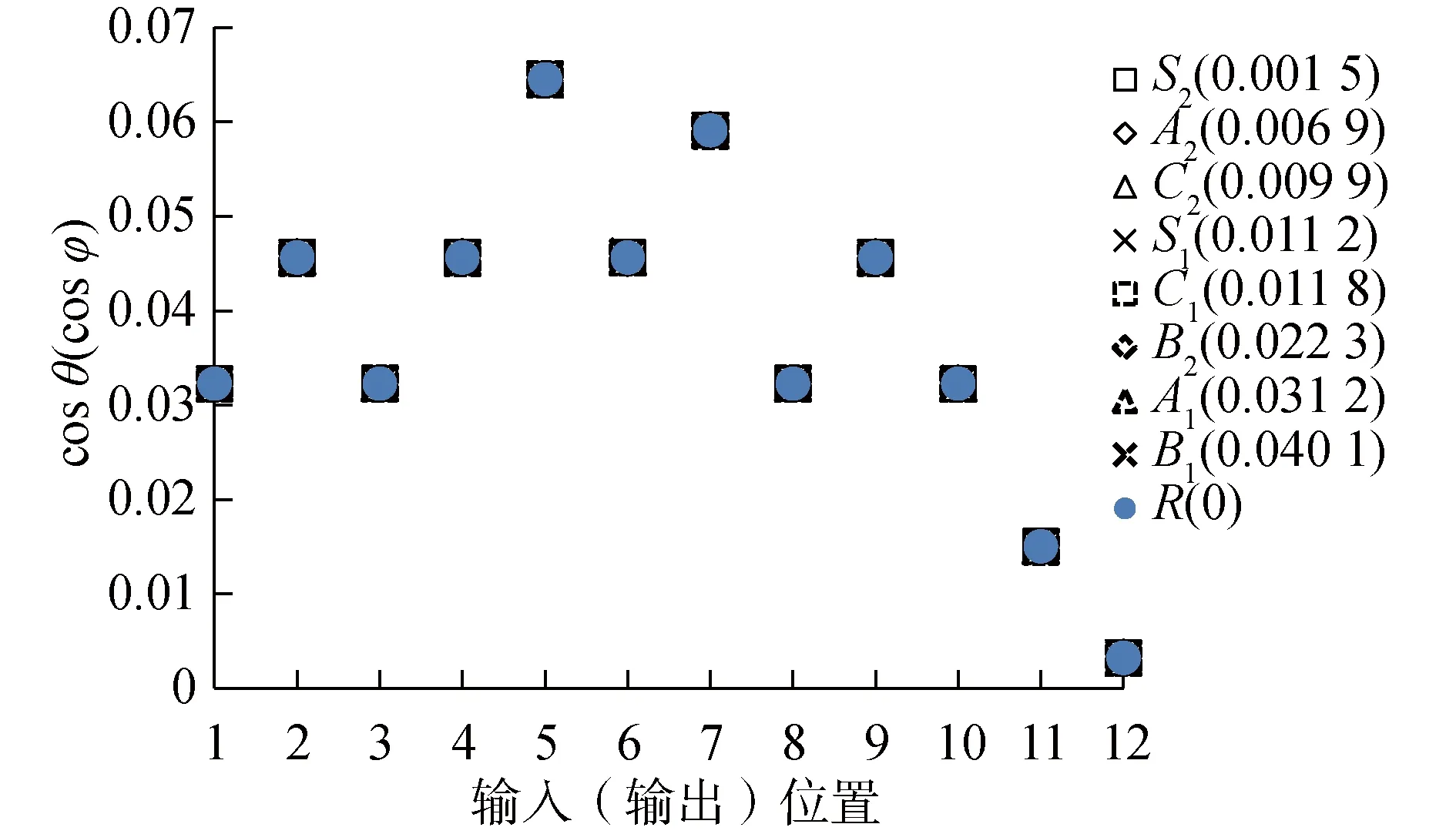
圖5 1×1階不同復雜度板可控性(可觀性)對比Fig.5 Comparison of controllability (observability) for damped plates with different complexities on 1×1 mode

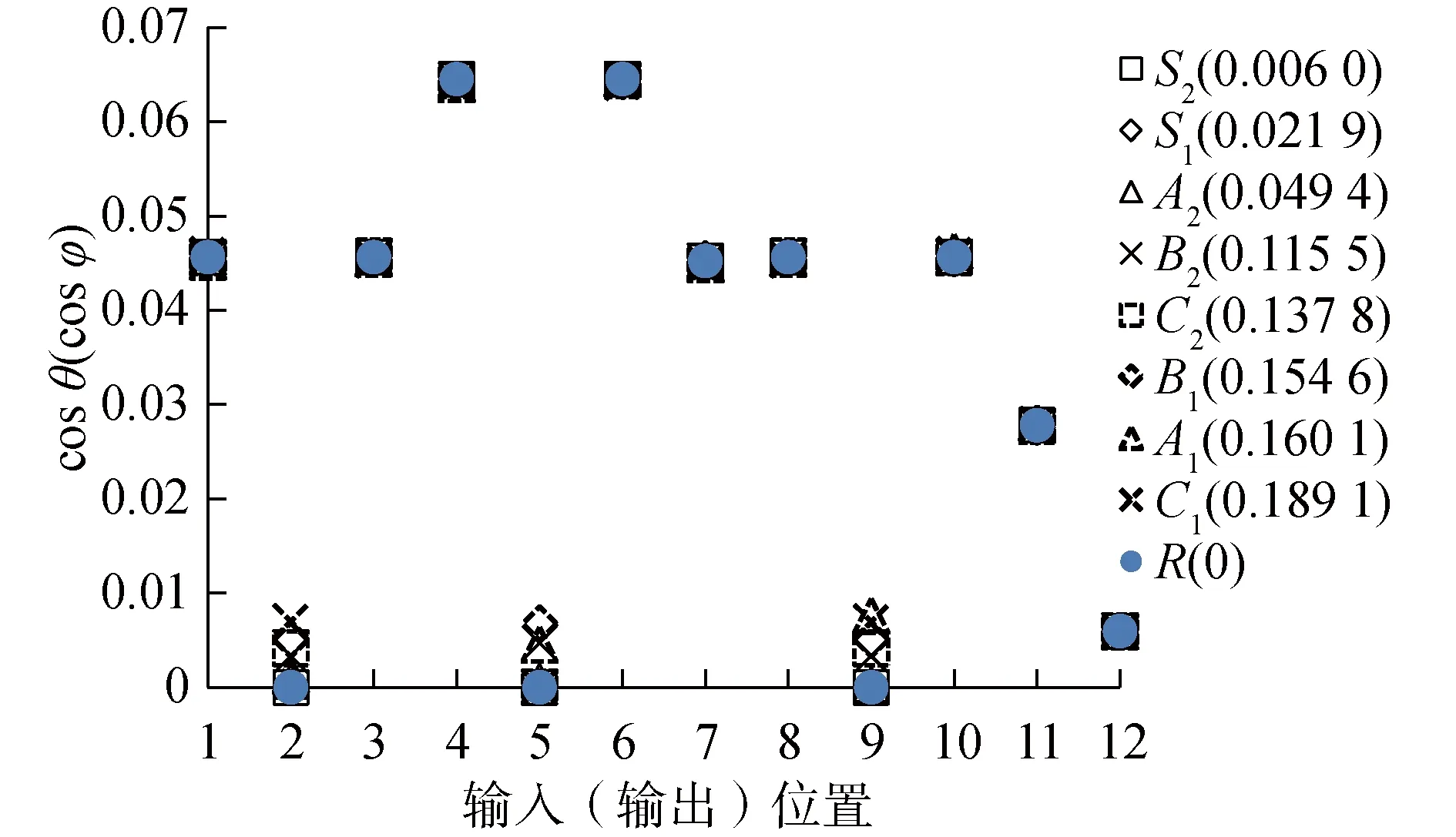
圖6 2×1階不同復雜度板可控性(可觀性)對比Fig.6 Comparison of controllability (observability) for damped plates with different complexities on 2×1 mode

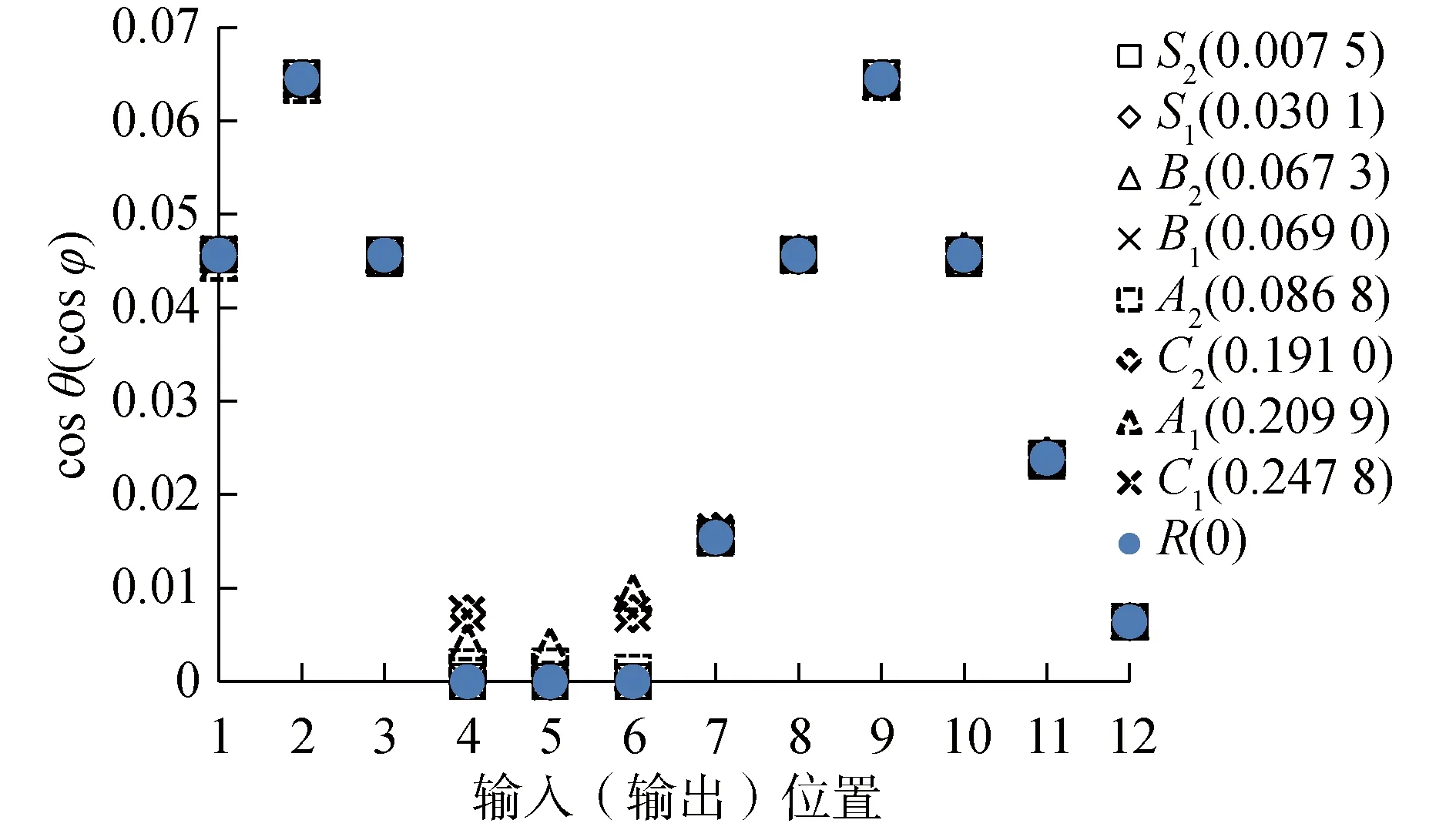
圖7 1×2階不同復雜度板可控性(可觀性)對比Fig.7 Comparison of controllability (observability) for damped plates with different complexities on 1×2 mode

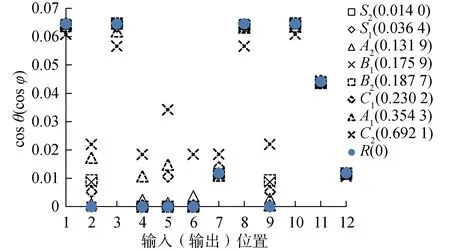
圖8 2×2階不同復雜度板可控性(可觀性)對比Fig.8 Comparison of controllability (observability) for damped plates with different complexities on 2×2 mode

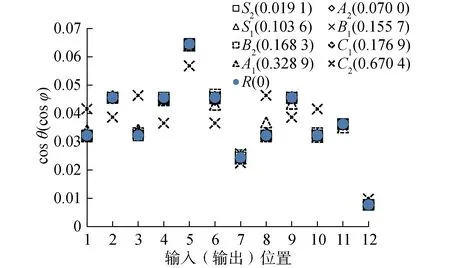
圖9 3×1階不同復雜度板可控性(可觀性)對比Fig.9 Comparison of controllability (observability) for damped plates with different complexities on 3×1 mode

由圖5～9可知，不同模態復雜度MPD值的阻尼板的可控性(可觀性)相比于復雜度MPD=0(實模態)的阻尼板變化可以分為3種情況：1) 當MPD<0.1時，或當0.10.3或0.10.3且輸入(輸出)點不在均勻阻尼板R實模態振型的節點位置時，可控性(可觀性)降低。綜上所述，復模態的模態復雜度對其可控性和可觀性的有影響，具體是對可控性和可觀性增強、降低還是不變，取決于所關心的輸入和輸出位置。

不可控和不可觀的位置(可控性(可觀性)指標為0)為輸入和輸出應該盡量避免的位置點。由圖5～9可知，均勻阻尼板R(實模態)存在不可控和不可觀點：2×1階模態的2、5、9號點；1×2階模態的4、5、6號點；2×2階模態的2、4、5、6、9號點。為了研究復模態復雜度對上述不可控和不可觀點的影響，計算了8種非均勻阻尼板2×1階模態的2、5、9號點，1×2 階模態的4、5、6號點以及2×2階模態的2、4、5、6、9號點的可控性和可觀性指標平均值，并繪制平均值隨復模態復雜度變化圖，如圖10所示。

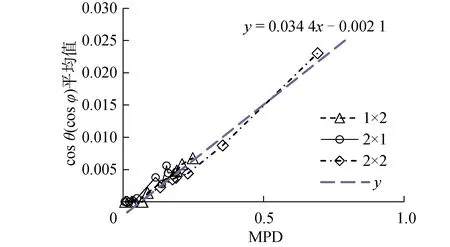
圖10 復雜度對指標平均值影響Fig.10 Influence of complexity on averagecosθs

由圖10可知，實模態情況下不可控和不可觀的點的可控性(可觀性)指標平均值隨著復模態的模態復雜度的增大呈增大趨勢，且其分布接近線性增長。因此，對3種模態下的計算結果進行線性擬合得到圖10中y所示擬合曲線。文獻[5]中認為，可控性(可觀性)指標cosθ(cosφ)<0.01時，該點對于該階模態而言是不可控(不可觀)的。通過擬合曲線y=0.034 4x-0.002 1可知，當MPD值小于0.351 7時，cosθ(cosφ)平均值均小于0.01。因此，在本文所研究算例下，從可控性和可觀性的角度去考慮復模態與實模態的區別時，當MPD<0.357 1時，復模態可簡化為實模態進行可控性(可觀性)的分析；當MPD>0.357 1時，復模態不能近似為實模態進行可控性(可觀性)分析。

綜上所述，本文認為，任意以復模態形式振動的結構，從可控性和可觀性的角度去考慮復模態與實模態的區別時，都滿足如下規律：當復模態的模態復雜度小于某一值時，復模態可簡化為實模態進行可控性和可觀性的分析；當復模態的模態復雜度大于某一值時，會對可控性和可觀性產生較大的影響，此時復模態不能近似為實模態進行可控性和可觀性分析。

4 結論

1) 在相同階模態和相同輸入和輸出位置，實模態情況下的與復模態情況下的結構振動的可控性和可觀性不同，且改變量與復模態的模態復雜度有關；

2) 復模態的模態復雜度對其可控性和可觀性的有影響，具體到是對可控性和可觀性增強、降低還是不變，取決于所觀測的輸入和輸出位置；

3) 從可控性和可觀性的角度去考慮復模態與實模態的區別：當復模態的模態復雜度小于某個值時，復模態可簡化為實模態進行可控性和可觀性的分析；當復模態的模態復雜度大于此值時，會對可控性和可觀性產生較大的影響，此時復模態不能近似為實模態進行可控性和可觀性分析。