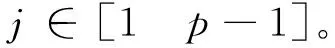張拉整體基本單元幾何穩定構型分析
王艷蒙, 劉賀平, 羅阿妮
(哈爾濱工程大學 機電工程學院,黑龍江 哈爾濱 150001)
隨著空間結構的迅速發展,傳統空間結構[1-5]已經不能滿足需求,因此發展新型空間結構受到了廣泛的關注。張拉整體結構是一種由離散的受壓桿件和連續的受拉索構件構成的一種自應力空間網格結構[6-11],張拉整體結構是一種自平衡體系[12-14],其穩定性是由結構參數和構件預緊力共同決定[15-17]。張拉整體結構還具有形狀美觀、構件結構簡單、質量輕盈、展納率高等特點[18-22]。本文從張拉整體基本單元進行構型參數分析,構型中p根桿必然對應p-1種構型,分析構型節點受力平衡獲得平衡條件來判斷斜索和桿及水平索空間位置關系,通過分析節點nd(i+j)分別處在相對節點nd(i)的4個象限位置來計算桿扭轉角與斜索p-1種連接方式之間的函數關系,獲得結構穩定時參數之間的函數關系,獲得穩定構型條件。
1 張拉整體基本單元
三桿張拉整體單元是張拉整體結構的基礎,此單元可以拓撲為具有更多桿構件的張拉整體單元,也可以通過拼接形成更多復雜結構的張拉整體結構。如圖1所示為張拉整體基本單元[28-29],此張拉整體結構包括3根桿和9條索,上端面圓周半徑ru、下端面圓周半徑rd、端面間高度h、上下端面平行、上下端面形心連線垂直兩端面、同一端面圓周上節點均勻分布;上下端面內的索為水平索,上下端面間的細實線為斜索,粗實線為桿構件。上下端面間的扭轉角為φ,這里稱為單元內旋轉角(這一角度為任意一根桿構件的2個端點在底面上的投影與底面圓心的連線夾角)。
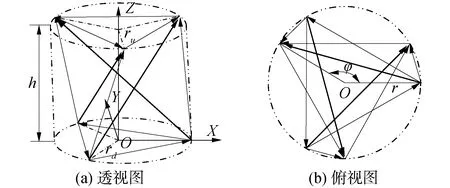
注:細實線為斜索,粗實線為桿構件圖1 三桿張拉整體單元結構簡圖Fig.1 Schematic diagram of three-bar tensegrity unit
2 基本單元幾何參數
為了建立張拉整體基本單元的數學模型,定義基本單元外形包絡幾何參數,上端面半徑ru,下端面半徑rd,單元高度h(具體分3種情況,如圖2所示,上下端面半徑相等rd=ru和上下端面半徑不等rd>ru和rd 圖2 基本單元外形包絡幾何柱或臺體Fig.2 Basic element shape envelope geometric column or table body 從構件組成的角度看張拉整體基本單元。桿構件個數p,2p根端面水平索,把2個端面分別圍成正p邊形,p根斜索均勻分布在兩端面之間。 從節點與構件的連接關系看張拉整體基本單元,任意節點均與4個構件連接:1根桿、3根索。每個節點同時與其所在端面內相鄰2個節點連接2個水平索,與另一個端面內的一個節點用1根桿連接,與另一端面除連接桿的節點之外的p-1個節點中的任一個節點,連接1根斜索,也即有p-1種斜索連接方式,相對應的桿繞z軸的扭轉角為φj,斜索繞z軸的扭轉角為βj。 通過以上分析,可以看出,p根桿必然對應p-1種構型(任意節點用1根桿連接另一端面的1個節點,則另一端面內仍然有p-1個節點,可以任選一個節點布置斜索),接下來探討這p-1種基本單元穩定構型的條件,及不同穩定構型獲得的結構中構件幾何參數。分析影響穩定構型的關鍵因素。 當張拉整體基本單元桿的構件數為p時,基本構型有p-1種連接方式,連接方式不同則桿、索繞z軸扭轉角φj,扭轉角βj的值不同。 選擇上端面節點進行分析(由于張拉整體單元結構具有對稱性,且上下端面的每個節點受力情況類似,均受3個索的拉力和一個桿的壓力),該節點受上端面2個相鄰的水平索的拉力、上下端面間桿的壓力和斜索的拉力如圖3所示(su(i+1)和su(i-1)為2個水平索、svi為斜索、gi為桿)。而上端面的2個水平索的合力指向上端面圓心。由于張拉整體單元處于平衡狀態,故節點受力處于平衡狀態。平衡意味著2個力等大共線且反向、或3個力必須構成封閉的平面三角形且力的方向要首尾相連。節點平衡應用該共點三力平衡條件來判斷斜索和桿及水平索空間位置關系,進一步深入到桿扭轉角與斜索p-1種連接方式,這3個平衡力確定了一個平面。 圖3 與上端面節點連接的構件及受力Fig.3 The member connected with the upper end face node and its force 上端面節點受到的3個力確定的平面與上、下端面的交線分別為直線ounu(p+i)、直線nd(i+j)nd(i)。單元的上下2個端面平行,所以2條交線必然平行。針對節點nd(i+j)分別處在相對節點nd(i)的4個象限位置來探討單元的相位角φj(同時也是桿繞z軸的扭轉角)及斜索繞z軸的扭轉角βj,設定下端面節點nd(i)處在x軸正方向。 規定逆時針方向為正方向,當節點nd(i+j)處在第一象限時(如圖4所示),節點nd(i+j)和nd(i)對應的圓心角θj為: 圖4 節點nd(i+j)位于第一象限Fig.4 The node nd(i+j) is in the first quadrant 由幾何關系確定桿繞z軸扭轉的扭轉角φj值:在三角形Δodnd(i+j)nd(i)中,θj角值已知,因為直線odnd(i+j)與直線odnd(i)為下端面半徑,所以等腰三角形的2個底角,角α和角δ相等。由于直線ounu(p+i)平行于直線nd(i+j)nd(i),同位角α和γ相等。由以上條件可得p-1種構型中,桿及斜索繞z軸的扭轉角與斜索連接方式j之間的函數關系。 由圖中幾何關系可知扭轉角φj、βj為: 因為直線ounu(p+i)平行于直線nd(i+j)nd(i),同位角相等: γ=α 又因為等腰三角形Δodnd(i+j)nd(i)的2個底角相等: α=δ 由圖中幾何關系得3個角的關系: 桿扭轉角φj、斜索扭轉角βj與p、j的函數關系為: 在直線ounu(p+i)的延長線與端面圓交點q,由于力qnd(i)在節點處與其他2個力構不成平衡,即構不成封閉的首尾相接的矢量三角形,節點不在平衡狀態,張拉整體結構單元不穩定,即不滿足平衡條件,舍棄該點。 當節點nd(i+j)處在第二象限時如圖5所示,規定逆時針方向為正方向,其中節點nd(i+j)和nd(i)對應的圓心角θj為: 圖5 節點nd(i+j)位于第二象限Fig.5 The node nd(i+j) is in the second quadrant 在三角形Δodnd(i+j)nd(i)中,θj角值已知,直線odnd(i+j)與直線odnd(i)為下端面半徑,等腰三角型的2個底角角α和角δ相等。由于直線ounu(p+i)平行直線nd(i+j)nd(i),內錯角δ和γ相等。由以上條件可得p-1種構型中,桿及斜索繞z軸的扭轉角與斜索連接方式j之間的函數關系。 由圖中幾何關系可知相位角φj、扭轉角βj: 因為直線ounu(p+1)平行于直線nd(i+j)nd(i),內錯角相等得: γ=δ 等腰三角形Δodnd(i+j)nd(i)的底角相等: α=δ 由圖中幾何關系得3個角的關系: 桿扭轉角φj、斜索扭轉角βj與p、j的函數關系為: 當節點nd(i+j)處在第三象限時如圖6所示,規定逆時針方向為正方向,其中節點nd(i+j)和nd(i)對應的圓心角θj為: 圖6 節點nd(i+j)位于第三象限Fig.6 The node nd(i+j) is in the third quadrant 在三角形Δodnd(i+j)nd(i)中,θj值已知,直線odnd(i+j)與直線odnd(i)為下端面半徑,等腰三角形的2個底角,角α和角δ相等。由于直線ounu(p+i)平行于直線nd(i+j)nd(i),內錯角δ和γ相等。由以上條件可得p-1種構型中,桿的繞z軸的扭轉角與斜索連接方式j之間的函數關系。 由圖中幾何關系可知扭轉角φj: φj=θj-γ 因為直線ounu(p+i)平行于直線nd(i+j)nd(i),內錯角相等: γ=α 又因為半徑相等的等腰三角形Δodnd(i+j)nd(i)底角相等: α=δ 由圖中幾何關系得3個角的關系: 桿扭轉角φj、斜索扭轉角βj與p、j的函數關系為: 當節點nd(i+j)處在第四象限時如圖7所示,規定逆時針方向為正方向,其中節點nd(i+j)和nd(i)對應的圓心角θj為: 圖7 節點nd(i+j)位于第四象限Fig.7 The node nd(i+j) is in the fourth quadrant 三角形Δodnd(i+j)nd(i)中,θj角值已知,直線odnd(i+j)與直線odnd(i)為下端面半徑,等腰三角形的2個底角,角α和角δ相等。由于直線ounu(p+i)平行于直線nd(i+j)nd(i),內錯角α和γ相等。由以上條件可得p-1種構型中,桿的繞z軸的扭轉角φj與斜索連接方式j之間的函數關系。 由圖中幾何關系可知扭轉角φj: φj=θj-γ 因為直線ounu(p+i)平行于直線nd(i+j)nd(i),內錯角相等: γ=α 等腰三角形Δodnd(i+j)nd(i)中底角相等: α=δ 由圖中幾何關系得3個角的關系: 桿扭轉角φj、斜索扭轉角βj與p、j的函數關系為: 1)穩定構型的條件獨立于基本單元的外形包絡幾何參數(上端面半徑ru,下端面半徑rd,單元高度h),只由桿數目p及連接同一節點的桿、斜索的另一端節點序號差j,確定單元的穩定性,且這2個因素一一對應,相互依存,滿足以下條件。 3)穩定構型中桿、斜索的扭轉角φj、βj滿足當節點nd(i+j)處于一、二象限時φj+βj=π,當節點nd(i+j)處于三、四象限時φj+βj=3π。 4)桿扭轉角φj與φp-j關于坐標系x軸對稱:φj+φp-j=2π。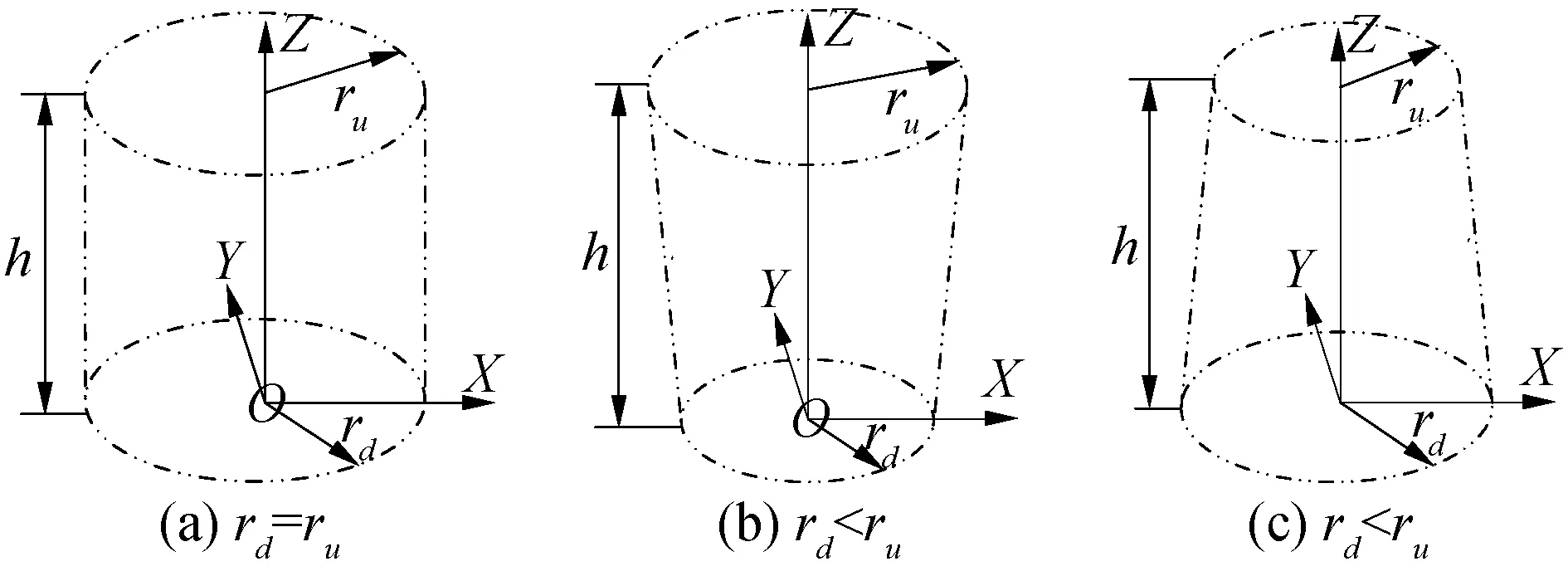
3 穩定構型影響因素分析
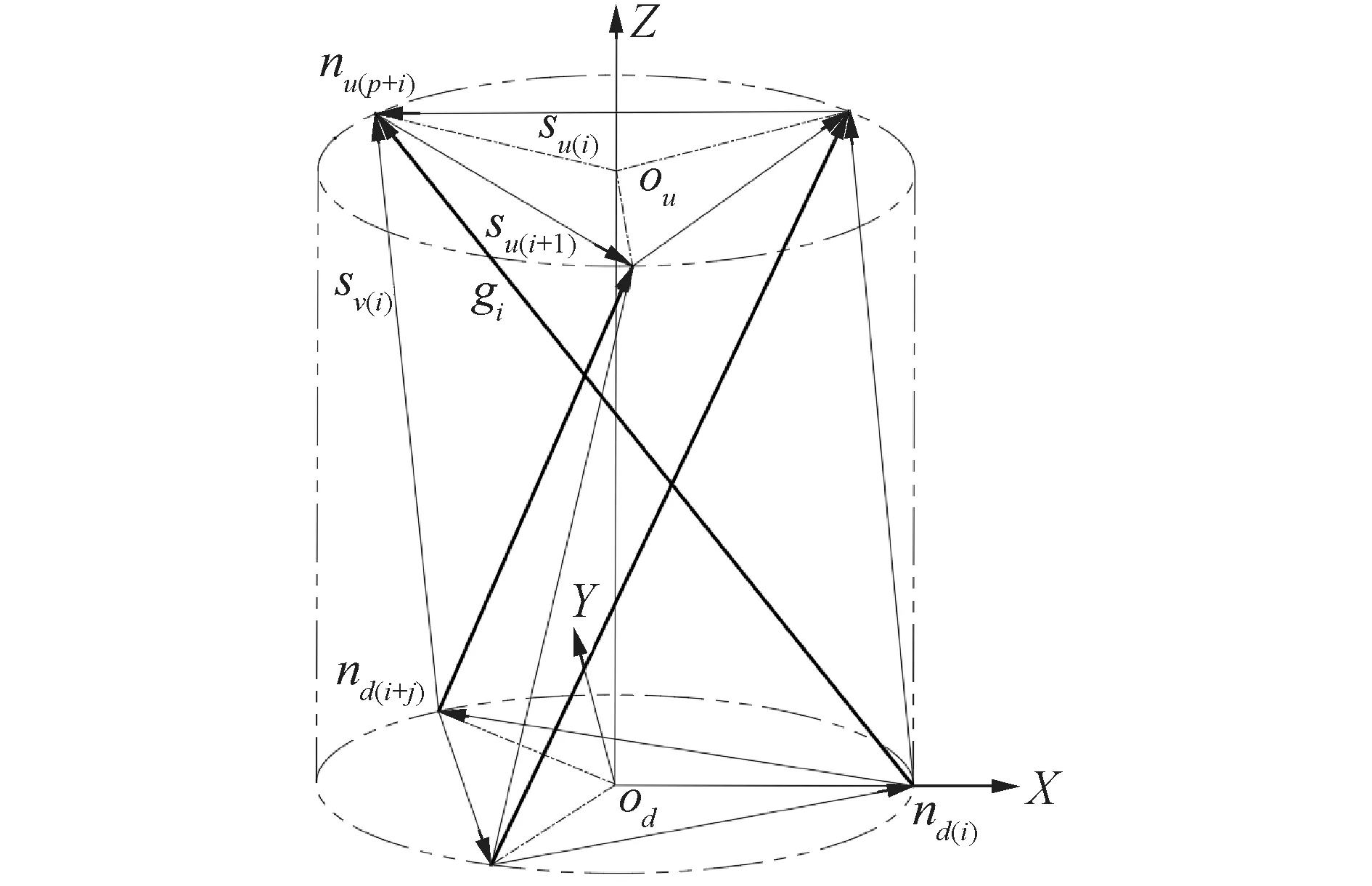
3.1 節點nd(i+j)處在第一象限
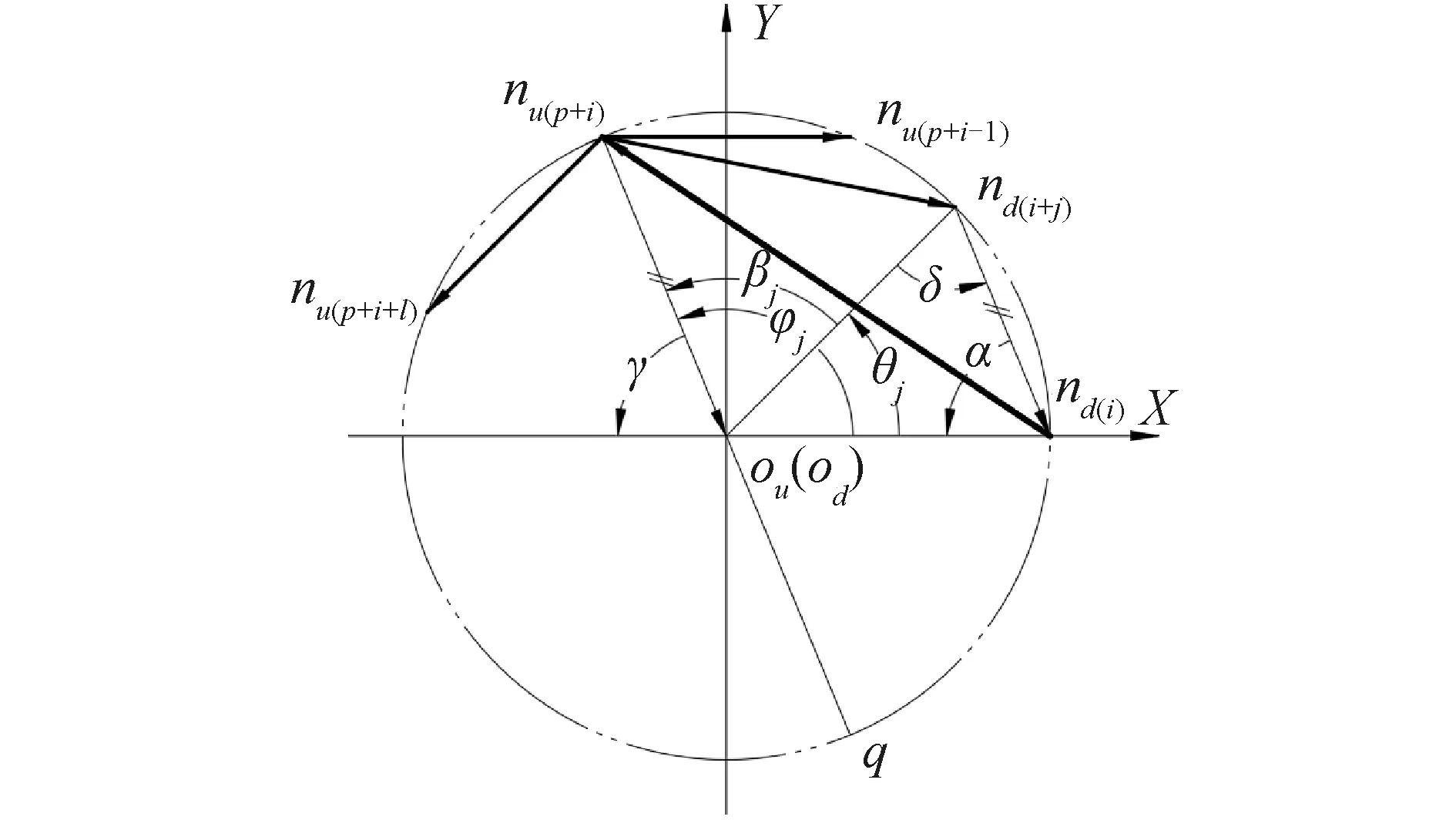
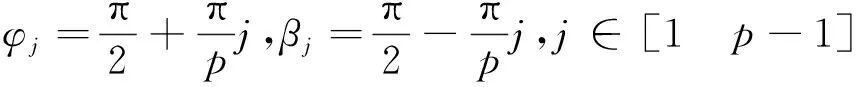
3.2 節點nd(i+j)處在第二象限
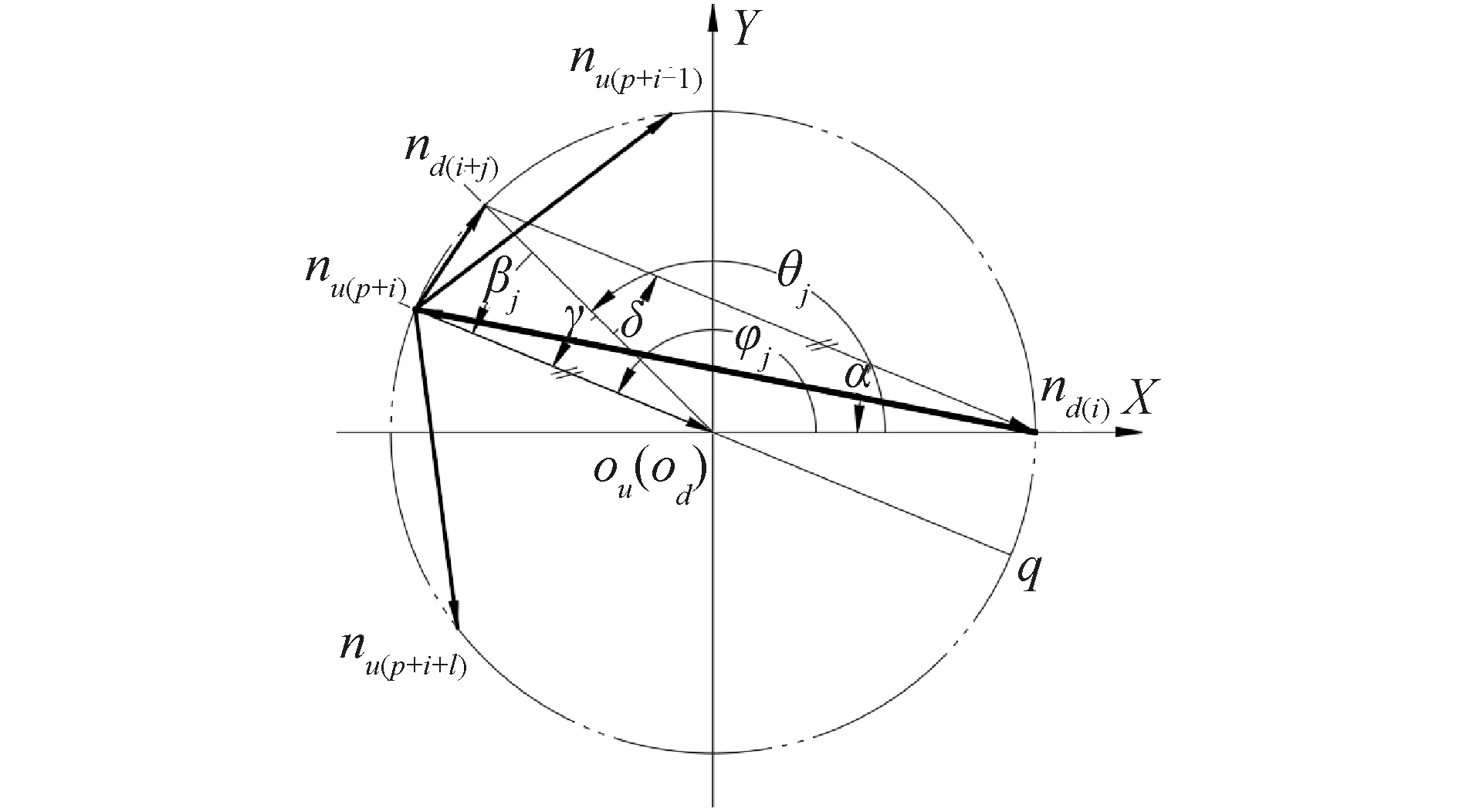
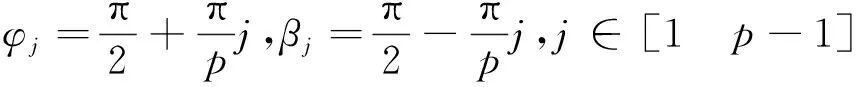
3.3 節點nd(i+j)處在第三象限
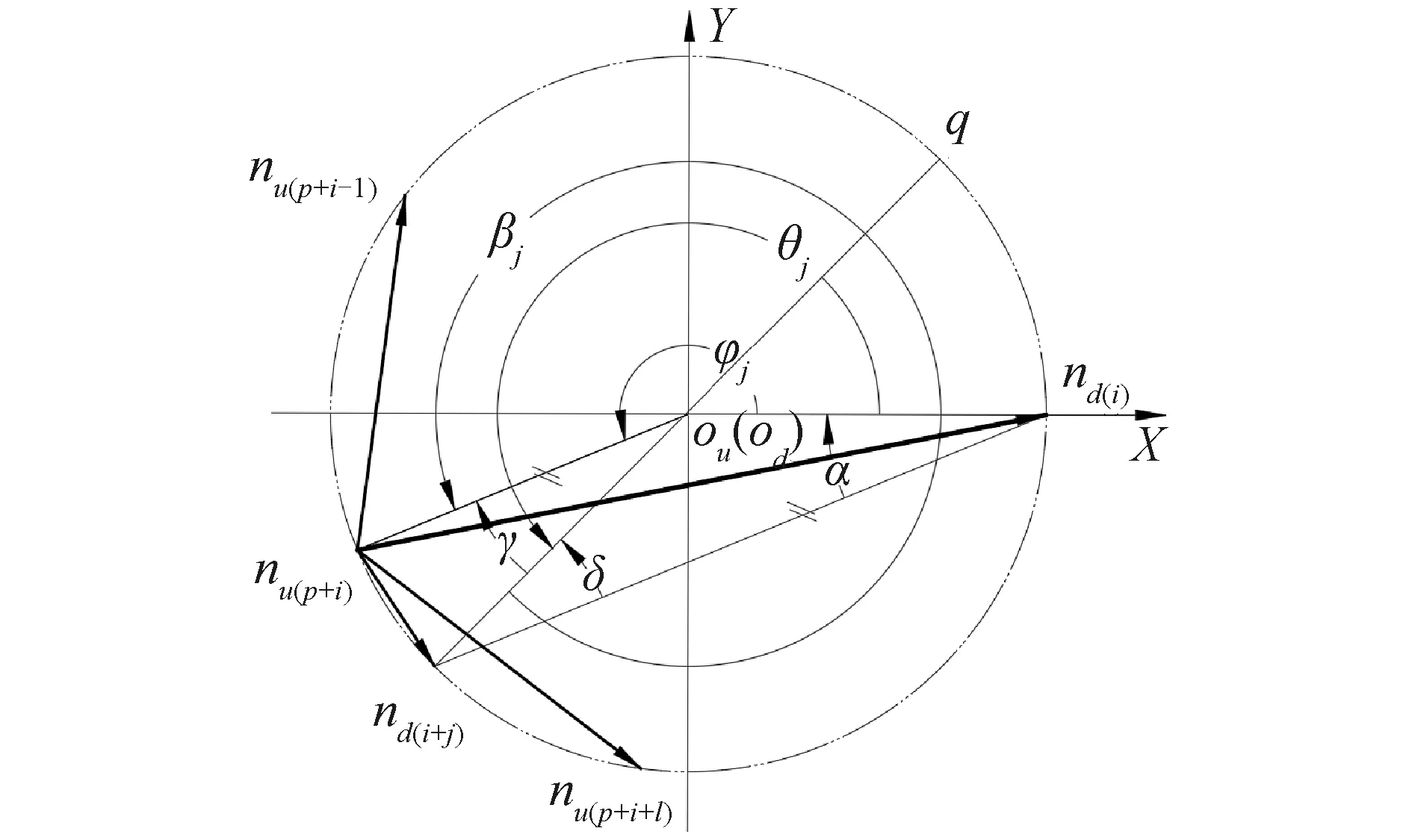
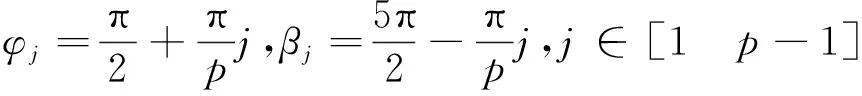
3.4 節點nd(i+j)處在第四象限
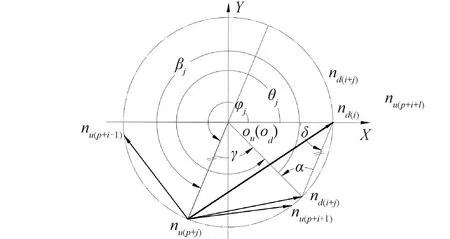
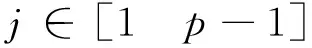
4 結論