基于Elmer開源有限元平臺的鐵氧體輔助同步磁阻電機的建模和分析

狄 沖 鮑曉華,2 潘 晉 王春雨

基于Elmer開源有限元平臺的鐵氧體輔助同步磁阻電機的建模和分析

狄 沖1鮑曉華1,2潘 晉3王春雨3

（1. 合肥工業大學電氣與自動化工程學院 合肥 230009 2. 合肥工業大學智能制造技術研究院 合肥 230009 3. 安徽皖南新維電機有限公司 合肥 230601）

該文以一臺物聯網車用鐵氧體輔助同步磁阻電機（FMaSynRM）為研究對象，以Elmer開源有限元平臺為核心，聯合運用其他開源軟件建立FMaSynRM二維磁場和電路耦合的瞬態有限元模型，重點闡述了其幾何建模、網格劃分、磁路耦合以及后處理可視化等環節的執行邏輯。在考慮逆變器輸出容量限制和主要工作點不同控制邏輯下，對FMaSynRM的鐵耗、銅耗、功率因數等主要性能指標進行分析計算，并將計算結果和場圖分布與商用有限元分析結果進行對比。最后對樣機進行加工和測試，獲得其在較寬調速范圍內的輸出功率圖和效率圖，并檢驗其主要性能指標，驗證了Elmer在電機電磁場有限元建模計算領域的可靠性和準確性，為其他類型的電機和電磁裝置的開源有限元建模提供參考和借鑒。

鐵氧體輔助同步磁阻電機 開源有限元 二維電磁場 場路耦合模型

0 引言

鐵氧體輔助同步磁阻電機（Ferrite Magnet assisted Synchronous Reluctance Motor, FMaSynRM）輸出轉矩中含有電磁轉矩和磁阻轉矩成分，并同時具備同步磁阻電機和永磁同步電機的主要特點[1]。FMaSynRM經過合理優化設計可以達到或者接近稀土永磁同步電機的性能，具有成本低廉、轉矩密度較高、效率較高、功率因數較高等特點[2]。目前，FMaSynRM已初步應用于家用電器、電動工具、電動汽車、航空航天等領域[3-5]。鑒于其上述特性和發展潛力，在電動物聯網車（即電動叉車）應用領域FMaSynRM將逐漸替代傳統感應電機，成為下一代主要驅動電機。

由于FMaSynRM的拓撲結構復雜，在設計電機電磁方案時，采用解析法分析計算較難取得令人滿意的結果。因此，目前學術界和工業界都采用有限元分析方法來分析、計算和設計FMaSynRM。通常，在電機電磁有限元計算領域，國內多采用商用有限元計算軟件Ansys Maxwell、Altair Flux和JMAG等來建模分析[6-8]。商用有限元計算軟件具有建模方便、精度高、可靠性好的特點。但具有底層代碼閉源、二次可開發性能差、價格昂貴等缺點。

鑒于商用有限元軟件存在上述缺點，業界對于底層代碼全部公開、能夠任意修改其源碼、可以免費使用的電磁場開源有限元軟件呼聲越來越高，且相應的研究也逐漸增加。目前，已經浮現出諸如FEMM、SMEKLIB和Elmer等適用于電機電磁場分析的開源有限元軟件[9-11]。其中FEMM含靜磁場和時諧場求解器，但不含瞬態求解器，已經應用于同步磁阻電機設計、無刷直流電機的退磁故障分析、雙饋開關磁阻電機設計等實際工程[9,12-13]。SMEKLIB雖然存在瞬態場求解器，方便進行磁場和電路相互耦合的非線性時步有限元計算，但軟件的其他方面并未完善，且缺少實際工程應用案例。

Elmer是一款由芬蘭IT研究中心（CSC–IT Center for Science）主導，聯合當地高校和科研機構共同開發，于2005年進行開源的通用多物理場有限元分析軟件[14]。其主要應用領域涉及流體力學、電磁學、聲學、結構力學等多個學科，并已經應用于諸多工程實例。此外，經過十幾年發展，由于Elmer的開源特性，其開發和維護已經區域國際化，其核心代碼和求解器一直以較高的頻率保持不斷的更新和維護。

Elmer在電機電磁場分析設計領域也有相關案例報道。在感應電機分析建模方面，J. Ker?nen采用Elmer二維瞬態場求解器，對一臺籠型轉子感應電機進行建模分析，重點考察Elmer的并行計算能力，并發現采用4個及以上CPU核心能極大縮短計算時間[11]。在永磁同步電機分析建模方面，P. Ponomarev則采用Elmer二維靜磁場求解器，對一臺表貼式永磁同步電機進行優化設計[15]。由于其優化維度尺寸多，采用不同轉子位置角的靜磁場模型來代替瞬態模型，共涉及866 700個二維靜磁場有限元仿真模型，因此P. Ponomarev利用超級計算機上共計200個CPU核心，耗時9h完成優化設計。上述兩個案例，分別驗證了采用Elmer瞬態和靜磁場求解器可以對電機電磁場進行有限元建模仿真的可能性，并重點檢驗了其良好的并行計算能力。此外，近些年，P. Ponomarev已經逐步開始嘗試采用Elmer對一臺永磁同步電機進行三維電磁場有限元仿真，并成功求解電機的平均電磁轉矩、鐵耗、銅耗及永磁體渦流損耗，取得了一定的進展[16]。然而，這些研究重點只落在Elmer求解器本身，缺少與商用有限元軟件的分析對比和樣機實驗的驗證。

在與商用有限元軟件分析對比分析方面，M. Zaheer以一臺5kW的感應電機為例，對采用Elmer和商用有限元軟件所計算的鐵耗進行詳細對比[17-18]。對比發現：在不同供電頻率下，Elmer在鐵耗計算方面和商用有限元軟件計算結果保持高度一致，并通過樣機測試驗證其準確性，但其研究僅側重于電機鐵耗的建模分析，在電機其他電磁性能方面并未詳細展開。

本文以電動物聯網車用FMaSynRM為研究對象，主要闡述以Elmer開源有限元平臺為核心建立FMaSynRM磁場和電路相耦合的有限元模型，所涉及的幾何建模、網格劃分、磁場和電路耦合、求解和后處理等環節皆采用開源軟件執行的案例。并在各主要工作點下結合合適的控制邏輯，將利用開源平臺和商用有限元軟件計算得到的轉矩、鐵耗、功率因數等電磁性能進行詳細對比，檢驗其計算精度。最后，對工程樣機進行測試，考察電機在主要工作點的電磁性能。

1 開源平臺下電機有限元建模

1.1 電機主要參數

本文研究對象為一臺下一代電動物聯網車用FMaSynRM。考慮其應用場景，其電磁性能方面的主要特點為需滿足在空載平地、滿載平地、滿載爬坡和坡道起步四個特定工作點下的轉矩轉速特性要求，其設計要求和性能指標見表1。

表1 FMaSynRM主要設計要求和性能指標

Tab.1 Main design and performance requirements of the FMaSynRM

表1中逆變器輸出最大相電流有效值為400A，根據繞組聯結方式則電機最大相電流有效值為230.94A。同時，逆變器直流母線電壓為80V，則輸出最大基波線電壓有效值為[19]

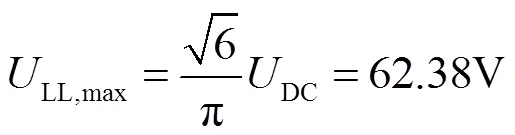
電動物聯網車平臺直流側可由蓄電池或者鋰電池供電，根據實際工程經驗，視其供電方式的不同，逆變器輸出基波線電壓有效值一般留有10%～20%的裕度。同時，為了方便更為靈活地調節電機繞組匝數，電機繞組將采用三角形聯結。

此外，依據實際工程經驗，在滿載爬坡點的基礎上將轉矩提高20%，可以視作坡道起步特性，因此表1中坡道起步轉矩為213.01N·m，轉速為718r/min。

1.2 以Elmer為核心的開源有限元電機建模

一般而言，電機電磁場有限元建模主要包括以下幾個重要環節：幾何模型建立、網格劃分、非線性材料定義、物理面定義、運動設置、求解器設置及可視化后處理等。本文主要以Elmer（主要含網格生成器ElmerGrid、求解器ElmerSolver等核心套件）開源有限元平臺為核心，聯合運用其他開源有限元前處理（如Gmsh、SALOME等）和后處理（如Octave、ParaView、Python等）軟件或編程語言，對電動物聯網車用FMaSynRM進行建模分析，其主要建模流程如圖1所示。

圖1 以Elmer開源平臺為核心的電機電磁場有限元建模流程

1.2.1 幾何模型和網格

在幾何模型建立以及網格劃分方面，為使網格能和ElmerGrid進行對接，一般可以采用Gmsh或者SALOME進行建模及剖分。兩者都是開源軟件，其中SALOME可以方便讀取各類CAD文件便于快速建模，而Gmsh則有利于幾何尺寸的參數化建模。

為了方便后續對電機幾何尺寸進行優化，本文采用Gmsh對電機進行幾何模型的建立和網格的劃分，并于模型各個幾何點設置剖分單元大小，其與商用軟件Altair Flux所建立的幾何模型和網格對比結果如圖2所示。從圖2中可以發現，Gmsh所建立的網格質量較高，且和Altair Flux所建立的網格較為相似。同時，兩者在二維有限元分析計算過程中都可以靈活采用一階和二階（3節點和6節點）三角形網格單元，便于建模時對模型計算速度與精度進行取舍。此外，值得注意的是Gmsh所建立的網格需要轉換為ElmerGrid所能接受的文件格式，才能進一步采用ElmerSolver求解器進行求解，進一步研究對比發現在轉換過程中網格文件的網格精度沒有丟失。

1.2.2 求解器和場路耦合

在求解器方面，ElmerSolver在二維電磁有限元瞬態場以磁矢位為主要求解變量，遵循下述電磁場統一方程[20]。

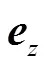
求解器經過合理部署包括：設置材料屬性、定義機械運動屬性、賦予物理面等，即可以進行初步分析計算。然而，為了進一步考慮繞組形式，則需要進行磁場和電路耦合仿真，根據電路各節點電流平衡和回路電壓平衡列舉方程，得到求解矩陣系數，并進行相應設置。FMaSynRM一般采用電流源激勵進行建模仿真，且通常商用有限元建模軟件（如Altair Flux）中都會將電流源三角形聯結等效轉換為星形聯結，因為電流源三角形聯結容易導致求解不收斂。同理，本文在考慮磁場和電路耦合時，也將采用上述星三角轉換進行等效處理。

以U相繞組為例，其電路連接示意圖如圖3所示。由基爾霍夫電壓定律和基爾霍夫電流定律在回路中列舉電壓回路方程和各節點列舉電流方程，可以得到

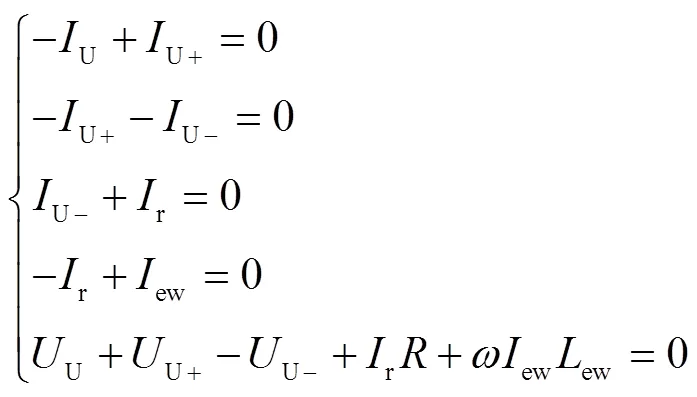
式中，IU為U相電流源電流激勵，A；IU+和IU?分別為U+和U?繞組電流，A； Ir為繞組相電阻電流，A；R為繞組相電阻，?；Iew為端部繞組電流，A；Lew為端部繞組電感，H；ω為交流供電電源角頻率，rad/s；UU+和UU?分別為U+和U?繞組電壓，V。繞組相電壓為磁場和電路耦合的核心，可由ElmerSolver瞬態求解器直接求得。

根據上述電壓電流方程，按式（4）列舉矩陣方程[14]，供求解器進行求解。

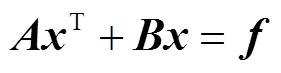
式中，和為系數矩陣；為電路中待求解向量；為激勵源。

1.2.3 求解結果后處理和可視化

在求解結果后處理和可視化方面，如圖1所示，采用ElmerSolver求解完畢后，按求解結果類型可以將其劃分為標量解（如轉矩曲線、電壓曲線等）和矢量解（磁通密度分布、磁力線分布等）。其中標量解可采用開源軟件/編程語言如Octave、Pyrthon等進行后處理并進行可視化；而矢量解則可采用開源軟件ParaView進行后處理和可視化。

本節重點介紹了以Elmer為核心的開源有限元電機建模邏輯，可以發現：整個建模流程涵蓋前處理、求解以及后處理，全程采用開源軟件來執行。并且Elmer擁有二維瞬態求解器，能夠執行磁場和電路耦合建模，滿足FMaSynRM電磁場有限元建模分析的要求。

2 開源平臺和商用軟件的仿真結果對比

依據前文建模邏輯，本節主要對比采用開源平臺和商用軟件（Altair Flux）對FMaSynRM進行有限元建模的結果，并重點考察電機在空載和帶載情況下的矢量解和標量解的差異。

2.1 空載情況下的仿真結果對比

FMaSynRM在空載情況下，采用Elmer和Altair Flux對其進行仿真的磁通密度和磁力線分布如圖4所示。從圖4中可以看出，兩者磁通密度分布幾乎一致，磁橋飽和處磁通密度大小較為接近。并且磁力線走向也高度相似。此外，兩者建立的都是1/4模型，采用奇邊界考慮其周期性，磁力線在邊界附近的走向皆符合其真實物理特性。

圖4 空載情況下電機磁通密度和磁力線分布對比

采用二維瞬態時步有限元對FMaSynRM進行仿真計算可以獲得電機空載時的主要電磁性能。空載情況下電機繞組端電壓隨時間變化曲線對比如圖5所示，對比發現，兩者空載端電壓誤差較小，并且保證在所有時刻誤差都保持在一個較小的范圍內。

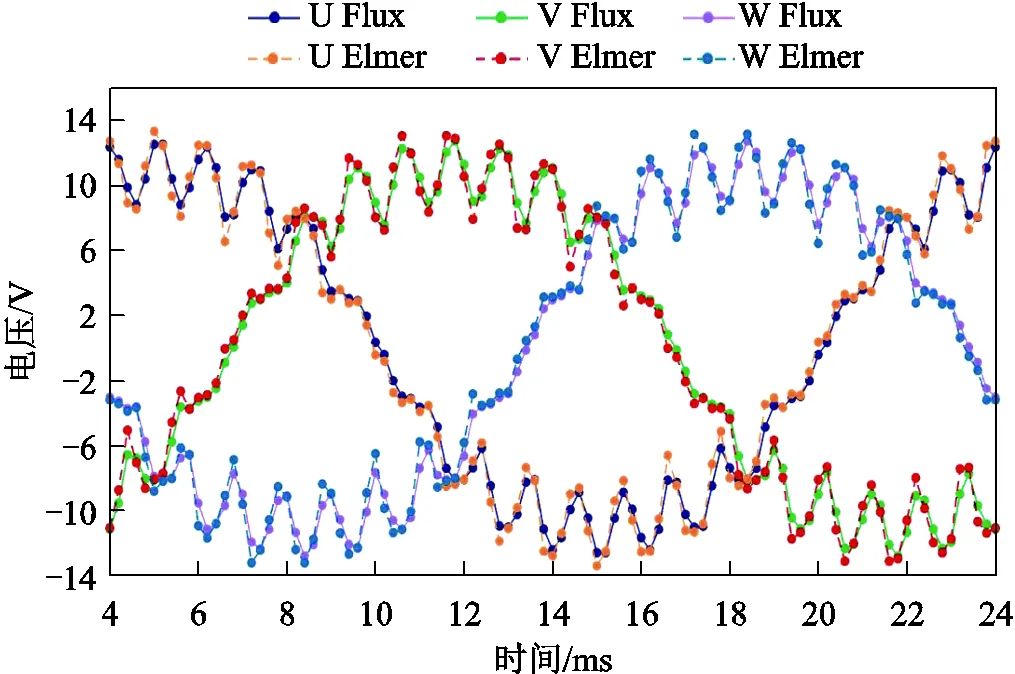
圖5 空載情況下繞組端電壓對比

磁鏈是FMaSynRM在分析設計過程中另一項關鍵性能參數，Altair Flux采用式（5）來求取繞組磁鏈。

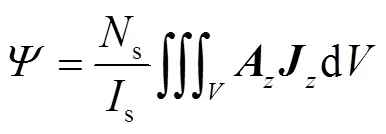
式中，s為每相串聯匝數；s為繞組相電流，A；為對應體積所在的區域。

在ElmerSolver求解器中，由于繞組反感應電動勢可以直接輸出。因此，在反感應電動勢基礎上直接求取繞組磁鏈，其公式可以表示為

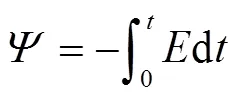
式中，為繞組反感應電動勢，V；為時間，s。

在空載情況下的電機三相繞組磁鏈隨時間變化的曲線對比如圖6所示。從圖6中可以看出，Elmer和Altair Flux輸出的繞組磁鏈幅值曲線形狀較為一致。但值得注意的是，Elmer采用式（6）中邏輯所計算的繞組磁鏈曲線落后于Altair Flux輸出的曲線半個時間步長，這是由積分處理所導致的誤差。該誤差可以通過減小仿真步長的方法進行有效抑制。

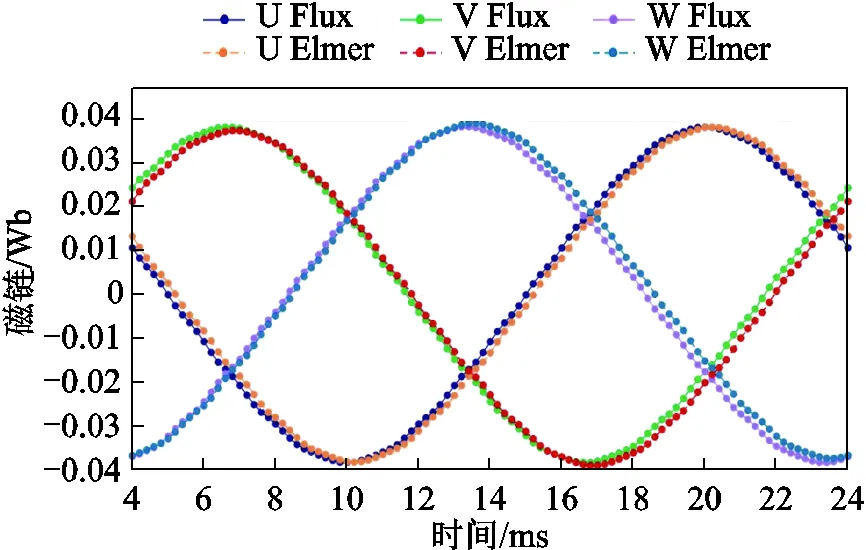
圖6 空載情況下繞組磁鏈對比

在電磁轉矩計算方面，Elmer和Altair Flux則分別采用了虛位移法和麥克斯韋張量法（Arkko’s method）進行求解，其主要表達式為[19]

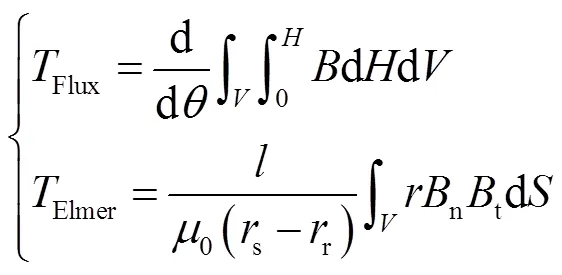
式中，、n和t分別為氣隙中的合成磁通密度、磁通密度法向分量和磁通密度切向分量，T；為氣隙中的磁場強度，A/m；為轉子位置角，rad；0為真空磁導率，H/m；s和r分別為定轉子氣隙內、外半徑，m；為力臂半徑，m；為氣隙所在的面域。

在空載情況下FMaSynRM齒槽轉矩隨時間變化的曲線對比如圖7所示。從圖7中可以發現，盡管兩種軟件采用不同邏輯計算轉矩，但其誤差時刻都保持在±2.5%以內，具有較高的精度。

圖7 空載情況下齒槽轉矩對比

2.2 帶載情況下的仿真結果對比

由于學界對FMaSynRM交直軸劃分并未達成統一共識，為了方便理解，本文采用永磁同步電機邏輯對FMaSynRM交直軸進行劃分。為了對比開源平臺和商用平臺下的FMaSynRM的帶載情況，下述對比都是在定子電流s= 50A，電流超前角= 90°（即d軸電流d= 0控制）條件下進行。

FMaSynRM在帶載情況下的磁場和磁力線分布對比如圖8所示。與空載情況下類似，經Elmer 和Altair Flux輸出的磁場和磁力線分布都具有較高的一致性。FMaSynRM在帶載情況下電磁轉矩隨時間變化曲線的對比如圖9所示。其中經Elmer求解的平均轉矩為9.92N·m，經Altair Flux求解的平均轉矩為10.50N·m，兩者誤差為5.5%。對比轉矩曲線可以發現，兩個軟件輸出轉矩具有一定的誤差，這有可能是轉矩求解方法和網格劃分不同所導致的，但整體誤差都處在一個可以接受的范圍內。

圖8 帶載情況下電機磁通密度和磁力線分布對比

圖9 帶載情況下電磁轉矩對比

3 FMaSynRM樣機性能分析和實驗驗證

3.1 FMaSynRM樣機性能分析

如表1所示，在考慮逆變器輸出容量的限制下，為滿足FMaSynRM在四個特定工作點特性，經過研究對比，采用正弦繞組形式可以滿足上述設計要求，其中每半槽導體數采用17和9交叉設置。鐵氧體采用四層結構，實測120℃下剩磁為0.335T。

依據表1中四個特定工作點，并從最大轉矩電流比控制（Maximum Torque Per Ampere, MTPA）、弱磁控制（Field Weakening, FW）和最大轉矩電壓比控制（Maximum Torque Per Voltage, MTPV）中選擇合適的控制邏輯（方法）對樣機性能進行分析，其主要性能指標見表2，其中的電壓和電流仍然是將三角形聯結等效為星形聯結進行分析計算的。

從表2中可以看出，在各工作點下，Elmer和Altair Flux采用相同的定子電流激勵和電流超前角，可以得到電機電磁轉矩、端電壓、銅耗、鐵耗和功率因數等電磁性能。對比各項性能指標可以發現，Elmer和Altair Flux兩者的求解結果都較為接近，具有較小的誤差，可見Elmer在電機電磁場分析計算領域具有較高的工程使用精度。其中兩者鐵耗采用的都是可以計及高頻鐵耗的改進的Bertotti模型進行求解計算[20-21]，即

表2 FMaSynRM在主要工作點下的電磁性能

Tab.2 Electromagnetic performances of the FMaSynRM at the main operating points

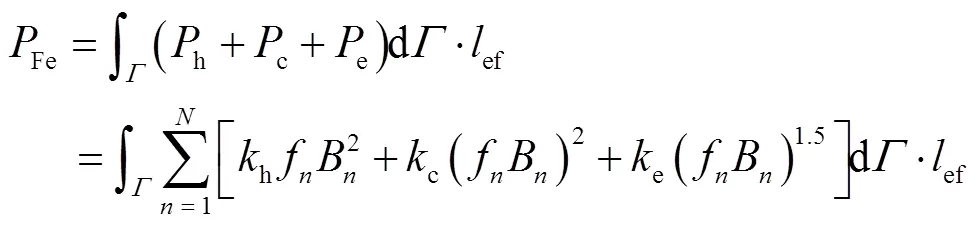
式中，h、c和e分別為磁滯、渦流和雜散（此“雜散”為“excessive”，并非傳統意義的“雜散損耗”）損耗，W/m3；h[W·s/T2/m3]、c[W/(T/s)1.5/m3]和e[W/(T/s)2/m3]為對應損耗系數（可由多頻-曲線擬合得到）；f為第次磁通密度諧波的頻率，Hz；B為第次磁通密度諧波的幅值，T；為定子所在的物理面；ef為鐵心軸向長度，m。

值得注意的是，一般情況下鐵氧體電阻率較大約100?·m，因此由高頻諧波引起的鐵氧體感應渦流損耗可以忽略不計，所以表2中未列舉鐵氧體渦流損耗。

3.2 樣機實驗測試結果

依據電機設計優化方案，對樣機進行加工，區別于其他類型電機，FMaSynRM最主要的特點為其轉子拓撲結構形式的不同。本文設計加工電機的轉子沖片如圖10所示，可以發現該轉子沖片和本文有限元所建立的模型高度一致。FMaSynRM樣機的測試平臺如圖11所示，測試時在保證不超出逆變器容量情況下，轉速由300r/min 增加到3 600r/min，步長300r/min；轉矩由10N·m逐漸增加到220N·m，步長10N·m；從而獲得電機功率和效率，考察電機在不同轉速和轉矩下的性能指標。

圖10 FMaSynRM樣機轉子沖片圖

圖11 FMaSynRM樣機測試平臺

圖12為樣機實測輸出功率和效率，從圖中可以發現，該FMaSynRM在如表2所示的幾個主要工作點附近的轉矩輸出基本符合設計要求。同時，可以發現該電機具有較寬的調速范圍，且其高效運行區間同樣較寬。

樣機實測性能與有限元計算結果的對比見表3。表3中選擇了較具代表性的工作點進行分析對比，工作點選擇原則為：轉速轉矩都涵蓋中低高范圍。從表3中可以發現，實測數據和有限元仿真結果在各個工作點下都較為接近，證明了商用Altair Flux軟件和開源Elmer軟件都具有較高的計算精度，符合工程計算要求。此外，觀察各工作點下電流可以發現，在同轉矩下對比，實測電流比有限元仿真計算電流略大，原因可能是加工制造過程中的誤差，以及定子采用了斜槽工藝，降低了定轉子之間的電磁耦合，使得對應轉矩輸出能力略微下降。

表3 樣機實測性能與有限元計算結果對比

Tab.3 The performance comparison of the tested and finite element simulated results of the prototype

4 結論

本文以Elmer開源通用多物理場有限元平臺為核心，詳細介紹了開源平臺下FMaSynRM的建模邏輯程序。具體涉及幾何模型建立、網格劃分、磁路耦合設置、求解結果后處理和可視化等多個方面。并將有限元仿真計算結果和商用有限元Altair Flux軟件計算結果進行詳細的對比。結果顯示，從電機場圖分布到轉矩、磁鏈隨時間變化曲線、鐵耗、功率因數等電磁性能，兩個平臺的計算結果都保持高度一致。

此外，本文還重點考察了FMaSynRM在多個特定工作點下的性能指標，并進行實驗驗證。實測結果顯示樣機具有較寬的調速范圍和高效運行區間，在不同轉速下的轉矩輸出水平基本符合設計要求。證明了Elmer開源有限元軟件在電機電磁場有限元建模領域的實用性和可靠性，為今后其他類型的電機和電磁裝置的設計提供了思路。

[1] 楊晨, 白保東, 陳德志, 等. 可變磁通永磁輔助同步磁阻電機設計與性能分析[J]. 電工技術學報, 2019, 34(3): 489-496.

Yang Chen, Bai Dongbao, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 489-496.

[2] 黃輝, 胡余生. 永磁輔助同步磁阻電機設計與應用[M]. 北京: 機械工業出版社, 2017.

[3] 王瑾, 李巖, 賈建國, 等. 反電動勢和凸極率對高效永磁同步磁阻電機穩態特性影響分析[J]. 電工技術學報, 2020, 35(22): 4688-4698.

Wang Jin, Li Yan, Jia Jianguo, et al. Analysis of the influence of back-EMF and saliency ratio on steady-state characteristics of a high efficiency permanent magnet synchronous reluctance motor[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4688-4698.

[4] 程明, 文宏輝, 曾煜, 等. 電機氣隙磁場調制行為及其轉矩分析[J]. 電工技術學報, 2020, 35(5): 922-930.

Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 922-930.

[5] 徐媚媚, 劉國海, 陳前, 等. 永磁輔助同步磁阻電機設計及其關鍵技術發展綜述[J]. 中國電機工程學報, 2019, 39(23): 7033-7043.

Xu Meimei, Liu Guohai, Chen Qian, et al. Design and key technology development of permanent magnet assisted synchronous reluctance motor[J]. Proceedings of the CSEE, 2019, 39(23): 7033-7043.

[6] Turner L R. 3-D field computation: the near-triumph of commercial codes[J]. IEEE Transactions on Magnetics, 1996, 32(4): 2945-2949.

[7] Jiang W, Jahns T M, Lipo T A, et al. Machine design optimization based on finite element analysis in a high-throughput computing environment[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 869-876.

[8] Di C, Petrov I, Pyrh?nen J J. Modeling and mitigation of rotor eddy-current losses in high-speed solid-rotor induction machines by a virtual permanent magnet harmonic machine[J]. IEEE Transactions on Magnetics, 2018, 54(12): 1-12.

[9] Hoffer A E, Moncada R H, Pavez B J, et al. A novel method for finite-element modeling of a commercial synchronous reluctance machine[J]. IEEE Latin America Transactions, 2018, 16(3): 806-812.

[10] Lehikoinen A, Davidsson T, Arkkio A, et al. A high-performance open-source finite element analysis library for magnetics in Matlab[C]//2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 486-491.

[11] Ker?nen J, Ponomarev P, Pippuri J, et al. Parallel performance of multi-slice finite-element modeling of skewed electrical machines[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.

[12] Usman A, Rajpurohit B S. Comprehensive analysis of demagnetization faults in BLDC motors using novel hybrid electrical equivalent circuit and numerical based approach[J]. IEEE Access, 2019, 7: 147542-147552.

[13] Gouda E, Salah H M. A proposed design, implementation and control of doubly fed switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 101-106.

[14] R?back P, Malinen M, Ruokolainen J, et al. Elmer models manual[M]. Helsinki: CSC–IT Center for Science, 2013.

[15] Ponomarev P, Petrov I, Bianchi N, et al. Selection of geometric design variables for fine numerical optimizations of electrical machines[J]. IEEE Transactions on Magnetics, 2015, 51(12): 1-8.

[16] Ponomarev P, Ker?nen J, Pasanen P. Electromagnetic transient finite element 3D modelling of electrical machines using open-source tools[C]//2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 2016: 1657-1661.

[17] Zaheer M, Lindh P, Aarniovuori L, et al. Assessment of 5 kW induction motor finite element computations with a commercial and an open-source software[C]// 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), IEEE, Istanbul, Turkey, 2019: 114-119.

[18] Zaheer M, Lindh P, Aarniovuori L, et al. Comparison of commercial and open-source FEM software: a case study[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6411-6419.

[19] Pyrh?nen J, Hrabovcova V, Semken R S. Electrical machine drives control: an introduction[M]. Chichester: John Wiley & Sons, 2016.

[20] Di C. Modeling and analysis of a high-speed solid-rotor induction machine[D]. Lappeenranta, Finland: Lappeenranta-Lahti University of Technology LUT, 2020.

[21] 張冬冬, 趙海森, 王義龍, 等. 用于電機損耗精細化分析的分段變系數鐵耗計算模型[J]. 電工技術學報, 2016, 31(15): 16-24.

Zhang Dongdong, Zhao Haisen, Wang Yilong, et al. A piecewise variable coefficient model for precise analysis on iron losses of electrical machines[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 16-24.

Modelling and Analysis of a Ferrite Assisted Synchronous Reluctance Machine Based on the Open-Source Platform Elmer

Di Chong1Bao Xiaohua1,2Pan Jin3Wang Chunyu3

（1. School of Electrical Engineering and Automation Hefei University of Technology Hefei 230009 China 2. Intelligent Manufacturing Institute of HFUT Hefei 230009 China 3. Anhui Wannan Xinwei Motor Co. Ltd Hefei 230009 China）

This paper takes a ferrite magnet assisted synchronous reluctance motor (FMaSynRM) as the study object. To establish the two-dimensional electromagnetic-coupled transient model of this FMaSynRM, this paper selects the open-source platform Elmer as the core solver and cooperates with some other open-source packages. The logic to build the geometry, generate the mesh, tune the electromagnet-coupled setting, conduct the post-processing is emphasized in this paper. With the consideration of the inverter’s capacity, the iron losses, copper losses, power factor etc. at main operating points are evaluated by Elmer and comparisons are made with the commercial software. Finally, the prototype is manufactured and tested. The out-put power and efficiency maps at different speeds are obtained and the results meet the design requirements. The reliability and correctness of the modelling of the FMaSynRM by Elmer is proven, which sets an example for the design of other machines and similar electromagnetic apparatus by the open-source platform.

Ferrite magnet assisted synchronous reluctance motor (FMaSynRM), open-source finite element method, two-dimensional electromagnetic field, electromagnetic-coupled model

10.19595/j.cnki.1000-6753.tces.210093

TM341

國家自然科學基金（51977055）、安徽省科技重大專項（201903a05020042）、高等學校學科創新引智計劃（BP0719039）和中央高校基本科研業務費專項資金（JZ2021HGQA0198）資助。

2021-01-18

2021-04-10

狄 沖 男，1991年生，博士，講師，研究方向為電機設計和電機電磁場開源有限元建模仿真技術等。E-mail：Chong.Di@hfut.edu.cn(通信作者）

鮑曉華 男，1972年生，博士，教授，博士生導師，研究方向為電機設計理論和技術等。E-mail：baoxh@hfut.edu.cn

（編輯 赫蕾）