基于物理觀念 突出問題的物理本質
——“硬幣悖論”問題的再探究

李德林

（山東省壽光中學，山東 濰坊 262704）

1 問題再現

如圖1所示，已知小圓的半徑為r，大圓的半徑是小圓的3倍，小圓繞大圓做勻速滾動（大圓靜止不動，兩圓無相對滑動）.當小圓繞大圓轉一圈時，小圓自轉幾圈？若此過程只需1s，求小圓圓周上的點繞其圓心轉動的線速度為多少？

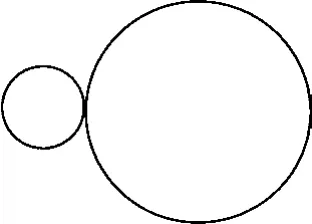
圖1

相似的問題曾經出現在1982年的美國的數學高考卷中，并且鬧出了烏龍事件，《紐約時報》對這件事進行了報道［1］，在當時引起了轟動，因為參與考試的30多萬人里只有3人答對，本題給出了1.5圈、3圈、6圈、4.5圈、9圈共5個選項，正確的答案是4圈，就連出題人也做錯，給出的5個選項里沒有正確答案，出題方美國大學理事會事后聲明，出題方的答案是錯的.

這個問題在數學上叫“硬幣悖論”，將兩枚相同的硬幣整齊的擺放，將上面的硬幣沿著下面的硬幣滾回原來位置，你會發現上面運動的硬幣實際轉了兩周，而不是我們想象中的一圈，這種反直覺的現象被稱為“硬幣悖論”.

2 基于物理觀念和思維，探究問題本質

文獻［2］從不同的角度，采用了“化曲為折”、質心（圓心）觀點、實踐驗證、數學繪圖軟件作圖等四種方法對這一問題進行了分析論證，其中 “化曲為折”的方法把圓周等效成多邊形，用的是一種等效思想，等效思想是分析物理問題時常用的一種思維方法，目的是把復雜的問題簡單化，抽象的問題具體化，文獻［2］中“化曲為折”的方法，反而使簡單的問題復雜化，直觀的問題抽象化，費時費力，特別是小圓在大圓內測滾動的情況，數學證明更為繁瑣，不利于學生理解小圓沿著曲線滾動的本質特點.

問題的實質在于小圓繞大圓公轉的過程中，即使沒有滾動小圓自身也發生了轉動，學生理解了這一點，問題就容易解決.可以先分析小圓沿著大圓滑動（沒有滾動）的情況，如圖2所示，A點為小圓上的一個固定點，假設小圓總是和大圓在A點接觸沿著大圓滑動一周，圖中標出了幾個特殊位置，可以看出小圓沿著大圓滑動了一圈小圓也自轉了一圈，也就是小圓繞大圓的公轉周期與小圓的自轉周期相同.這可類比為一個同學沿著一個圓形操場跑步，假設某一時刻面向南，經過了半圈變成了面向北，身體繞質心轉動了半圈，再經過半圈又成了面向南，也就是沿著操場跑了一圈身體也自轉了一圈.

圖2

理解了上述規律，當小圓沿著大圓滾動（無滑動）時，小圓的自轉圈數就水到渠成容易解決，先算出小圓相對大圓的滾動圈數，小圓的自轉圈數就是小圓相對大圓的滾動圈數加1，為什么是加1而不是減1，由圖2可以看出，小圓沿著大圓的公轉方向和小圓的自轉方向一致，當小圓沿著大圓順時針滾動時，小圓的自轉方向也是順時針.

如果小圓沿著大圓的內側滾動，小圓沿著大圓的公轉方向與小圓的自轉方向相反，當小圓沿著大圓順時針滾動時，小圓的自轉方向為逆時針（如圖3），因此小圓的自轉圈數就是小圓相對大圓的滾動圈數減1.

圖3

此方法原理簡單、省時省力，透過現象看本質，避免了建立復雜的數學模型和繁瑣的數學證明.

3 兩個圈數為什么不一樣

本題中小圓相對于大圓滾動了3圈，小圓也確實自轉了4圈，文獻［2］分析了求小圓自轉圈數的多種方法，但是兩個圈數為什么不同，學生還是感到疑惑，還是不理解問題的實質.

我們說小圓沿著大圓滾動，是地面上的人看到的運動形式，顯然是以地面為參考系的運動描述，而小圓自轉是相對于小圓的轉軸或圓心來說的，是以小圓的轉軸或圓心為參考系的運動描述，題目中求小圓邊緣上點的線速度也是相對于圓心的速度.因此小圓運動的兩種不同描述是相對于不同的參考系來說的，小圓的滾動圈數是地面參考系內的圈數，小圓的自轉圈數是圓心參考系內的圈數，而小圓的圓心相對于地面參考系又在運動，選擇的參考系不同，運動形式就不一樣，所以圈數不一樣，學生明確了這一點才能理解兩個圈數不同的本質.

4 質心（圓心）解法的理論依據

文獻［2］中根據小圓的質心運動求自轉圈數的方法，解法簡便但是學生不理解其中的原理，文中的理論依據是，由于小圓運動的路程是其圓周上的點繞質心轉動造成的，那么其圓周上的點相對于質心運動的弧長等于質心運動的路程，這樣說明，學生不知其所以然，理解起來有困難.

要求小圓圓周上的點的相對于其圓心的弧長，先求其相對于圓心轉動的線速度，因為存在兩個參考系，需要搞清楚牽連速度、相對速度和絕對速度三者間的關系.如圖4所示，設小圓圓心相對于地面速度為v1，小圓圓周上的點相對于其圓心的線速度為v2，因為小圓相對于大圓無滑動，所以小圓圓周上與大圓接觸的點相對于地面的速度為0，即絕對速度為零，所以牽連速度v1和相對速度v2等大反向.因此小圓圓心運動的路程等于小圓圓周上的點相對于圓心運動的弧長，這就是根據小圓質心（圓心）運動解法的理論依據.

圖4

這個解法可以推廣到一般情況，不管小圓沿著直線滾動還是曲線滾動都成立.

5 問題拓展

古希臘著作《論力學》里面有這樣一個問題，是一個讓當時不少偉大的數學家感到困惑的謎題，困擾當時數學界幾百年.

在輪上有兩個同心圓，如圖5所示，輪子滾動一周，從A點移動到B點，這時AB的距離等于大圓的周長，此時小圓也正好轉過1周，并走過了AB的距離，這不表明小圓周長和大圓相等嗎？

圖5

圖6

該問題可以建立數學模型分析，［3］但需要有較強的數學思維能力，如果基于物理觀念和思維，通過構建物理模型，容易分析清楚問題的本質.因兩個圓同軸轉動，大圓滾動一圈，小圓的滾動圈數和自轉圈數也都是一圈，在圓心參考系內，兩圓圓周上的點角速度相同，設大圓、小圓半徑分別為R和r，圓周上的A、C兩點在圓心參考系的線速度大小分別為Rω和rω，設圓心運動速度為v0，因輪子沿地面滾動（無滑動），所以與地面接觸點A點在地面參考系中速度為零，所以牽連速度v0和相對速度Rω等大反向（如圖6），即v0＝Rω，對于小圓上的C點，則v0＞rω，絕對速度vC＝v0－rω.這說明小圓上的C點在地面參考系中的速度不為零，小圓不是純滾動，在滾動的同時還有滑動，因此AB之間的距離要大于小圓的周長.小圓半徑r越小滑動速度越大，當小圓的半徑無限小，小圓就收縮成了輪子的圓心，就只有滑動沒有了滾動.

6 結束語

雙圓滾動問題，容易被現象和直覺所蒙蔽，認不清問題的實質，這樣的問題如果單純靠建立數學模型（如文獻［2］中的“化曲為折”）去分析，過程會比較復雜，也認不清問題的本質；如果基于物理觀念、滲透物理思維，通過建立恰當的物理模型去分析，容易看清問題的物理本質，［4，5］問題往往會迎刃而解.