基于改進模擬退火算法的PCB 電子元器件熱優化布置研究

吳沐羿，李先允，王書征

（南京工程學院電力工程學院，江蘇南京 211167）

“摩爾定律”指出集成電路板上晶體管的數量每過18 個月便會增加一倍。芯片計算能力呈現指數級增長的同時，相關問題也亟待解決[1]：電子設備晶體管數量急劇增加，導致集成電路板出現漏電現象甚至過熱擊穿，影響使用效率和壽命。

自1970 年以來，國內外學者對PCB 板上電子元件的散熱優化技術有大量研究：文獻[2]基于模擬退火算法實現了若干個PCB 元器件的陣列優化，并且用Icepak 進行仿真驗證。文獻[3]以150 kW 直流充電樁為研究對象，借助仿真軟件分析內部流體場和溫度場，通過正交試驗法對散熱器結構進行優化。文獻[4]采用遺傳算法對光伏并網逆變器的元器件位置進行優化，對散熱器的選型進行對比并進行仿真驗證。

綜合參考上述已有研究，文中提出一種PCB 電子元器件優化布置的熱設計方法。根據PCB 尺寸大小，建立元器件位置的二維陣列式布置模型，用改進的模擬退火優化算法對二維陣列式布置模型與元器件選位順序分別進行優化，且用ANSYS Icepak 熱仿真軟件進行驗證。

1 電子元件布置模型

根據相關文獻，在此類問題的研究過程中，PCB板上各電子元器件的布置問題屬于平面優化布置問題。為方便研究的進行，需要建立PCB 板上功率元器件的模型，實現數學模型的搭建[5-8]。PCB 板與功率元器件的熱學模型均定義為矩形，如圖1 所示。搭建二維陣列式布置模型，在矩形PCB（500 mm×480 mm）上均勻分布五行四列（共計20 個）矩形位置，以放置電子元件，并按從左下到右上的順序由1～20 依次編號。為實現程序編寫，將PCB 板上功率元器件的排列方式定義為解空間X，解空間X的第k個元素對應該位置上放置的元器件的編號，如：假設當前PCB 板上放置20 個電子元件，則PCB 板上電子元件布置的解的形式為X={x1,x2,…,x20}，其中，x1,x2,…,x20各自對應某電子元件的編號。向量形式的解X則對應元件的布置方案。文中所述的20 個電子元件中，1～5 號的發熱功率為3 W，6～10 號的發熱功率為5 W，11～20 號的發熱功率為8 W。

圖1 二維陣列式布置模型示意圖

2 模擬退火算法改進

2.1 算法改進思路

模擬退火算法是一種基于迭代求解策略的隨機尋優算法[9-11]，最早由Metropolis N 等人于1953 年提出。其思想源于固體退火原理，從某一個較高初始溫度出發，在不斷降溫的過程中，從解空間里隨機尋找目標函數的全局最優解以實現優化。模擬退火算法的主體流程可以簡單概括為如下步驟[12-14]：

Step1 規定新解生成的規律或函數，確定目標函數，并且生成一個初始解以實現后續迭代；

Step2 計算新解與舊解的目標函數差值，并且將兩個解的值對于原數學模型的優劣進行對比評價；

Step3 判斷新解是否被接受，通常判斷的依據是Metropolis 準則；

Step4 將上一個步驟判斷完畢后的解作為下一次迭代的解；

Step5 判斷是否達成終止條件或迭代次數。若是，則結束算法并得出最終解；若否，則繼續Step2 進行迭代。

該文的研究目的是實現PCB 板上功率元器件的散熱優化，使用Matlab 軟件進行算法程序的編寫，并對模擬退火算法進行如下改進設計：

文中的優化過程分為兩次：二維陣列式布置模型的優化以及在此優化基礎上進行的元器件選位優化。二維陣列式布置模型的優化方法如下：通過模擬退火算法對上文所述的20 個矩形位置各自沿著x或y方向進行任意距離的正向或反向移動，得出該方案下的目標函數值，并且多次迭代尋找最優陣列模型；元器件選位優化方法如下：由二維陣列式布置模型優化完畢后，在最優陣列模型中尋找元器件選位的最優方案。文中的優化布置實施過程如圖2 所示。

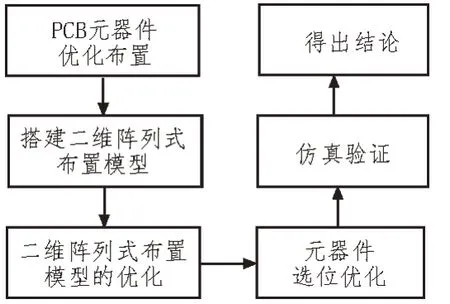
圖2 優化布置實施過程

2.2 目標函數與接受準則

為尋找最佳散熱布置方案，算法的目標函數需要準確體現不同距離與功率元器件之間的溫度影響。差分法、有限元法、有限容積法都可以用于電子元器件表面溫度的計算，但由于計算過程繁瑣，并不適合用作溫度評價函數。現選取一階熱設計公式[4]，在該公式基礎上進行相應修改后作為算法的溫度評價函數，即算法的目標函數。該熱設計公式的擬合多項式如下：

式（1）是元器件自身溫度評價公式，其中，Pi為元器件i的功率；Pmax為元器件最大功率。

式（2）是其他元器件貢獻溫度評價公式，其中，Dji為元器件j到元器件i的距離；Ri為元器件i的封裝半徑。

則總體溫度評價函數如式（3）所示：

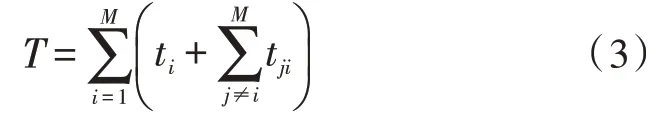
二維陣列式布置模型優化的新解生成準則：隨機抽取某矩形位置并確定方向及距離，這使得陣列模型的結果有多種可能。

元器件選位優化的新解生成準則：采用二變法，即對于某一迭代下的解空間X={x1,x2,…,xa,…,xb,…,xn}，通過對兩個隨機數a、b的生成，將兩個位置的元器件進行位置互換，得到新解X’={x1,x2,…,xb,…,xa,…,xn}，新解生成方法的示意圖如圖3 所示。

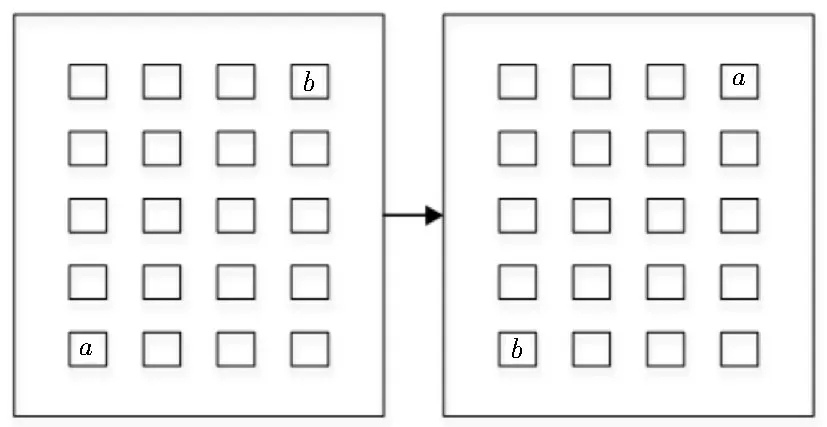
圖3 新解生成方法的示意圖

模擬退火算法對于新解的接受與否采用Metropolis 準則，即以式（4）作為依據：

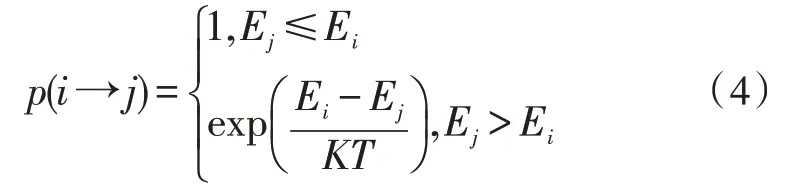
式（4）中，p為接受新解的概率；Ei、Ej分別是算法迭代過程中的第i代狀態和第j代狀態，并且i=j+1；K為Boltzmann 常數，是涉及溫度及能量的物理常數；T為算法每一次迭代后的溫度值。

3 熱仿真準備流程

該文借助目前主流的熱分析軟件Icepak 進行仿真。Icepak 使用計算流體力學（Computational Fluid Dynamics,CFD）軟件里精度較高的Fluent 求解器進行運算，借助ANSYS 建模軟件可以準確搭建相關模型[15-16]。

3.1 搭建仿真模型

針對文中涉及的仿真模型，在基于其幾何封裝的基礎上自建模型，借助軟件自帶的模塊進行仿真模型搭建。

模型需要對求解區域進行定義，以“Cabinet”模塊作為求解區域，模擬電子產品的實體外殼；PCB 板作為發熱模塊，借助方腔“Enclosure”模塊實現與電子產品其他部分的隔熱；模型的進出風口均采用濾網“Grille”模塊；散熱器采用“Heatsink”模塊，其類型以及翅片參數都會影響散熱效果；電子元器件采用“Source”熱源模塊建立，大型三維元器件采用“Block”建立，各模塊需要具體設置其屬性參數。

3.2 網格劃分及求解設置

對所搭建的模型進行網格劃分是熱仿真的重要步驟，網格劃分質量的優劣直接影響求解精度以及收斂與否。Icepak 提供3 種網格劃分類型——Mesher-HD 網格、非結構化網格、結構化網格。文中選取非結構化網格，其可對規則的幾何體進行貼體劃分，與文中仿真模型相匹配。

在對模型劃分完網格后，還需對所求解進行如下設置：

環境溫度默認為20 ℃，計算域流體設定為空氣，并且各類參數均為默認數值（比熱容、熱導率、壓強）；設置為湍流Zero equation 模型；設置重力加速度g方向并保持默認數值，海拔保持默認數值；忽略輻射換熱；迭代步數設置為20 次。

4 仿真并分析

為驗證文中所述的PCB 電子元器件優化布置方法的可行性，用軟件Matlab 編寫程序、Icepak 進行仿真，并與傳統PCB 板熱布局優化方法進行對比。

根據傳統PCB 板散熱優化方法，借助Matlab 優化程序對模型的元器件布置進行優化，得到傳統優化后的布置方案，如圖4 所示。將其布置模型搭建后，進行熱仿真，為避免不必要的系統誤差，網格劃分及求解設置與上文相同，仿真結果如圖5 所示。

圖4 傳統優化后的布置方案

圖5 傳統優化仿真結果圖

由圖5可以看出，用傳統散熱優化方法優化后，PCB板上最高溫度為49.931 4 ℃，最低溫度為19.999 3 ℃，最大溫差為29.932 1 ℃。

在此基礎上用文中所述方法進行優化。首先進行二維陣列式布置模型的優化，通過Matlab 軟件實現模擬退火算法尋優。為防止迭代次數過多或者陷入局部最優，經過多次仿真測試，確定算法迭代次數為100 次。如圖6 所示，進行大約70 次迭代后，溫度評價函數值實現了相對穩定。選取該結果下的二維陣列式布置方案，并搭建新的模型，二維陣列式模型優化后的布置方案如圖7 所示。二維陣列式模型優化仿真結果如圖8 所示。

圖6 模擬退火算法迭代結果圖

圖7 二維陣列式模型優化后的布置方案

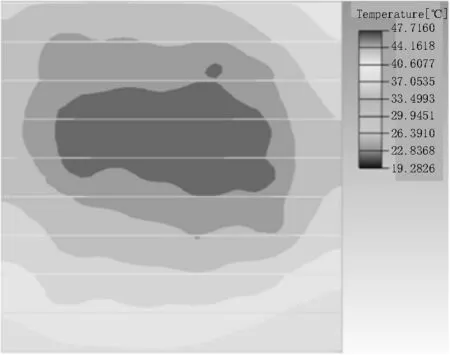
圖8 二維陣列式模型優化仿真結果

由圖8 可以看出，進行了二維陣列式布置模型的優化之后，元器件之間的距離相對變遠，使得局部溫度過高的現象有所緩和，并且高溫區域的分布更加勻稱。PCB 板上最高溫度為47.716 0 ℃，最低溫度為19.282 6 ℃，最大溫差為28.433 4 ℃。

再進行元器件選位優化，借助Matlab 軟件實現算法尋優。考慮到目標函數為熱設計的擬合多項式，與實際物理規律具有一定誤差，在多次仿真測試后選定迭代次數為20。迭代優化后，元器件的選位優化后的布置方案如圖9 所示。并且對模型的功率進行調整，其仿真結果如圖10 所示。

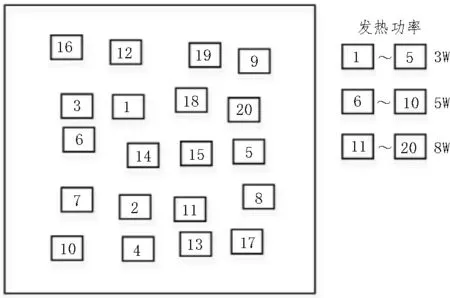
圖9 選位優化后的布置方案

由圖10 可以看出，進行了元器件選位優化之后，密集的8 W 元器件變得分散，原本高溫分布區域的形狀被改變，并且高溫面積有明顯縮小。等溫線分布均勻，溫度變化趨緩。PCB 板上的最高溫度為46.837 9 ℃，最低溫度為19.583 9 ℃，最大溫差為27.254 0 ℃。

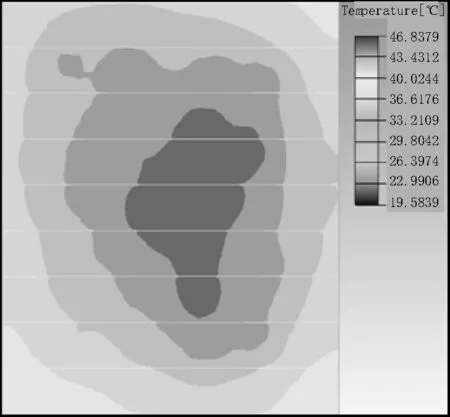
圖10 選位優化仿真結果圖

表1 是3 次仿真溫度結果的匯總，結合仿真圖不難看出，進行優化之后PCB 板最高溫度下降，雖然最低溫度相較第一步的優化有所升高，但總體而言，高溫面積得到有效地減小。

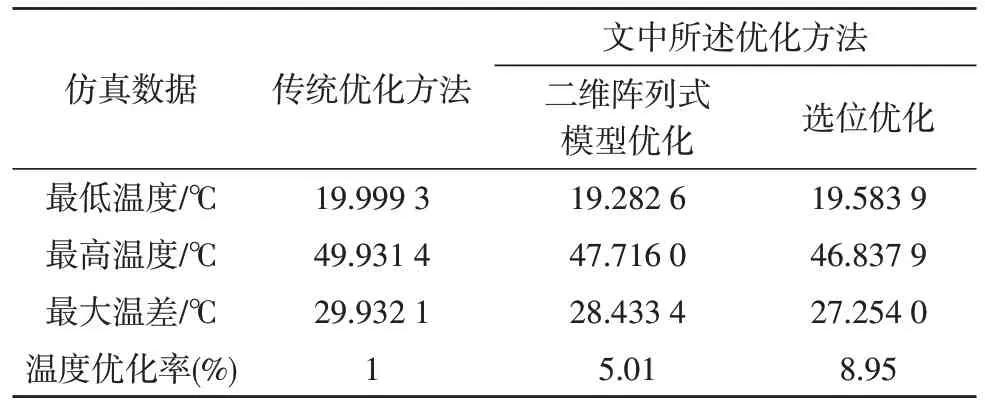
表1 仿真溫度匯總表

5 結論

文中在PCB 散熱優化方法的研究基礎上，提出一種基于改進模擬退火算法的PCB 電子元器件優化布置方法，該方法能較靈活地優化PCB 板上元器件的散熱。仿真結果表明，該方法經過兩個步驟的優化后，使PCB 的溫度比傳統散熱優化方法低3.09 ℃，優化率達8.95%，對散熱的優化有一定的效果。