求解0-1背包問題的融合貪心策略的回溯算法

j

j

j

j

i

n

i

x

i

C

C

i

14.else

15.break;

i

n

x

i

v

i

i

x

i

19.return maxvalue

O

n

O

n

O

n

n

O

n

n

1.3 0-1背包問題的經典回溯算法

與貪心算法相比，經典回溯算法更看重問題的整體性分析。經典回溯算法是使用深度優先遍歷求解0-1背包問題的經典算法。在問題求解的過程中，回溯算法將物品的選擇狀態構造成一個解空間樹，通過遍歷解空間樹中的每個節點來尋找問題的可行解和最優解。具體地說，經典的回溯算法從解空間樹的根節點出發，依次判斷解空間樹的每一個節點，并選擇當前狀態下滿足問題約束條件的節點，當遍歷到葉子節點時，算法對當前各個節點的選擇狀態進行記錄和判斷，當約束條件不滿足時，回退一步至上一狀態或回退多步，直至遍歷過解空間樹的每一個節點并回溯到根。在搜索的過程中，回溯算法會不斷判斷是否存在更優的解，并記錄和更新目前已找到的最優解。

經典回溯算法解決0-1背包問題的主要步驟如下：

(1)構造問題的解空間樹；

(2)確定問題的約束條件。一個是放入背包的物品總重量不超過背包的容量，另一個是放入背包的物品是否構成問題的最優解；

(3)從根節點開始，深度優先遍歷解空間樹，在遍歷的過程中根據問題的約束條件選擇性地進行回溯和繼續遍歷。

O

1.3.1 遞歸回溯算法

存在兩種實現經典回溯的算法，一個是遞歸算法，一個是非遞歸算法。遞歸回溯算法，是指把一個大型的復雜問題分解為一個與原問題相似的、規模較小的問題，通過遞歸求解小問題并將子問題的解合并，從而得到原問題的解。

算法2給出了遞歸回溯算法(knap1)的偽代碼描述，該算法從位于解空間樹根節點的第1個物品開始遍歷，依次考慮當前選中物品不放入背包和放入背包時，所有物品的選擇狀態。當遍歷到葉子節點時，進行最優解的約束條件檢驗并判斷是否進行回溯，算法的主要步驟如下：

(1)引入cw和cv分別表示當前狀態下背包內物品的總重量和總價值；

(2)對于每一個物品，首先選擇“不裝入背包”并進行遞歸，而在進行“裝入背包”的選擇前，則需要判斷所有選中物品的總重量是否滿足背包的容量；

(3)當遍歷到最后一個物品時，計算此時背包內物品的總價值，判斷是否為問題的最優解。

算法2：遞歸回溯算法knap1。

Initialize maxvalue, cw, cv as 0

knap1(1)

output maxvalue

intknap1(int i)

if i=n+1 then

if cv>maxvalue then

maxvalue←cv;

result←x;

else

x[i]←0;

knap1(i+1);

if cw+w[i]≤C then

x[i]←1;

cv←cv+v[i], cw←cw+w[i];

knap1(i+1);

x[i]←0;

cv←cv-v[i], cw←cw-w[i];

returnmaxvalue

1.3.2 非遞歸回溯算法

與遞歸回溯算法不同，非遞歸回溯算法利用物品的狀態值判斷是否需要回溯，而不需要借助操作系統提供的遞歸機制，因而一般具有較高的時空效率。

算法3給出了非遞歸回溯算法(knap2)的偽代碼描述，在該算法中，選中物品在進行“裝入”或“不裝入”背包的選擇前，其狀態值首先會被賦值為-1(代碼第2行)；當物品的選擇狀態確定后，其狀態值則為0或1(代碼第4、15行)；一旦該物品的狀態值增加至2時，則需要進行回溯(代碼第17、18行)。

算法3：非遞歸回溯算法knap2。

i

x

i

i

x

i

x

i

i

n

j

n

x

j

w

j

x

j

v

j

10.if cw≤C and cv>maxvalue then

11.maxvalue←cv;

12.result←x;

13.cw←0, cv←0;

14.else

i

x

i

17.else

i

19.end

20.return maxvalue

2 融合貪心策略和剪枝策略的回溯算法

2.1 問題分析

使用貪心算法求解0-1背包問題時，算法從問題的某一初始解出發，選擇當前條件下的最優解，并試圖構造或逼近問題的整體最優解。貪心算法每一步的決策僅考慮當前的局部信息，其解空間不可回溯再現，具有較強的隨機性和不可預知性。這種基于經驗或直覺的判斷，并不一定能夠保證找到問題真正的最優解，在絕大多數情況下，貪心算法得到的解只是問題的近似最優解。但是，由于貪心算法采用局部最優決策，因而往往具有較高的效率。

回溯算法的思想和枚舉法類似，即通過嘗試問題所有可能的解來尋找問題的最優解，這種算法雖然確保了解的正確性，但是以犧牲算法運行時間為代價。當問題規模較大時，回溯算法的運行時間呈指數式增長，在短時間內可能無法得到問題的最優解。

針對上述特征，該文將貪心算法的高效性和回溯算法的最優性相結合，提出了一種融合貪心策略和剪枝策略的新型回溯算法，簡稱新型算法。考慮到貪心算法得到的解雖然可能不是問題的最優解，但至少一定是問題的近似解，故將其作為初始解應用于回溯算法，從而可以盡快實現剪枝操作，進而提高回溯算法效率。

因此，新型算法將貪心算法的解作為回溯算法中剪枝策略的判斷條件，同時優化了遍歷過程中的約束條件，從而在確保得到問題最優解的同時，可以進一步提高算法效率。

2.2 新型算法

算法4給出了所提出的新型算法的偽代碼描述。該算法使用遞歸方法求解0-1背包問題，與經典的回溯算法不同，首先，算法4增加了基于價值的剪枝策略，若背包內物品的總價值與未遍歷到的物品的總價值之和小于算法1得到的解，則進行剪枝并回溯。其次，在遍歷的過程中，算法4優化了物品選擇的約束條件，將經典回溯算法的約束條件“放入背包的物品總重量不超過背包的容量”修改為“當前選中的物品重量滿足背包的剩余容量”。

所提出新型算法的主要步驟如下：

i

(2)算法1得到的解存儲到maxvalue_greedy中；

i

C

(4)首先判斷選中物品“不裝入背包”時是否需要剪枝；

(5)若選中物品“裝入背包”，首先判斷物品重量是否滿足背包的剩余容量，若“能裝入”，則繼續進行步驟4的剪枝判斷，最終確定物品的選擇狀態。

算法4：新型算法。

C

i

2.maxvalue_greedy←greedy()

C

4.output maxvalue

i

i

n

i

n

v

i

x

i

4.if value>maxvalue then

5.maxvalue←value;

6.result←x;

7.else

v

i

i

v

i

w

i

11.if pv+rv>maxvalue_greedy then

x

i

i

i

w

i

v

i

v

i

x

i

15.return maxvalue

在新型算法中，遞歸函數GB(第3行)的含義是：若當前考慮的物品“不裝入背包”，計算此時背包內物品的總價值與未遍歷到的物品的總價值之和，若大于maxvalue_greedy，則表明，在當前物品的選擇狀態下，存在將某些物品裝入背包后使得總價值提高的可能，因此進行遞歸；否則，表明在當前物品的選擇狀態下，任何后續的裝入選擇都將不可能超過現在背包內物品的總價值，此時則進行剪枝并回溯。若當前選中物品想要“裝入背包”，首先判斷該物品的重量是否滿足背包的剩余容量，然后繼續判斷是否“有必要裝入”。當遍歷到最后一個物品時，計算此時背包內物品的總價值并判斷是否為問題的最優解。

新型算法的核心思想是：對于每一個物品，只有該物品“能裝入背包”且“有必要裝入”，才會將其放入背包中。

3 仿真實驗與分析

3.1 實驗環境

該文進行了大量的仿真實驗，具體實驗環境為：CPU：i7-8550U，內存：DDR2 16 GB；硬盤：1 TB；緩存，8 MB；PF使用率：36%～45%；編程語言：Java，軟件開發工具：Eclipse。分別實現了遞歸回溯算法(算法2)、非遞歸回溯算法(算法3)和新型算法(算法4)，并在不同問題規模下進行仿真實驗與分析。

n

f

f

f

3.2 實驗結果分析

f

n

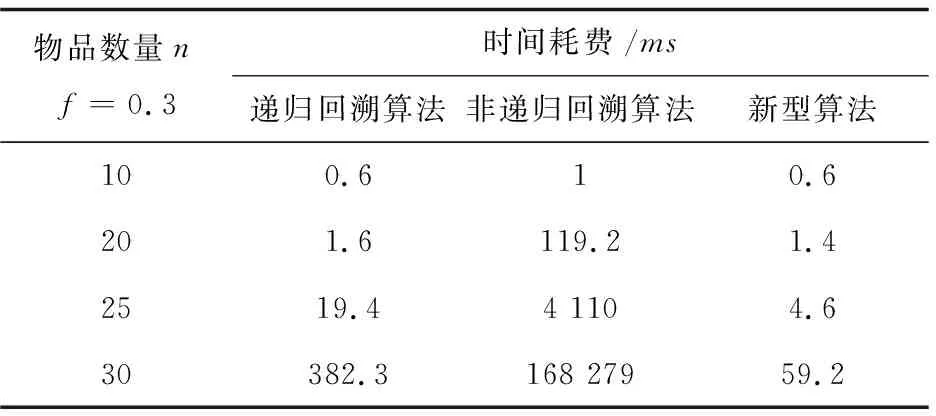
表1 三種算法在實驗系數f=0.3的時間耗費

表2 三種算法在實驗系數f=0.6的時間耗費

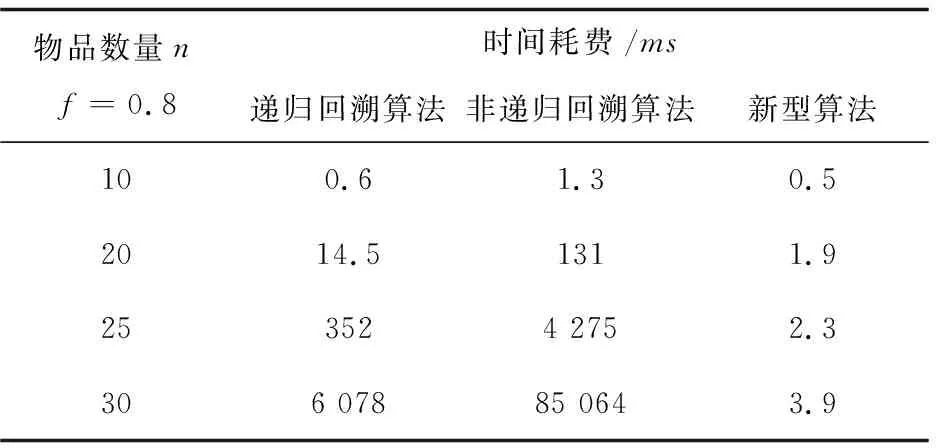
表3 三種算法在實驗系數f=0.8的時間耗費

通過上述比較，可以得出以下結論：

(1)在不同實驗系數下，隨著問題規模的增加，所有算法的時間耗費都呈現上升趨勢，其中經典的遞歸回溯算法和非遞歸回溯算法的上升趨勢更為顯著。結合算法的時間復雜度可知，經典回溯算法的時間耗費隨著問題規模的增加呈指數級增長。此外發現，非遞歸回溯算法較遞歸回溯算法具有較高的運行時間。

(2)在同一實驗系數、同一問題規模下，與經典回溯算法相比，該文所提出的新型算法在保證得到問題的最優解的同時，具有較小的時間耗費，特別是在問題規模較大時，效果更為明顯。

在不同實驗系數下，對遞歸回溯算法(算法2)和非遞歸回溯算法(算法3)的時間耗費進行了對比，從而驗證實驗系數是否對經典回溯算法的執行時間產生影響。實驗結果見表4。

表4 經典回溯算法在問題規模n=20時的時間耗費

根據表4可知，當實驗系數從0.3逐漸增加至0.9時，遞歸回溯算法的時間耗費線性增長至某一數值后，在該數值處呈現小幅度波動；非遞歸回溯算法的時間耗費則始終在某數值處小幅度波動。

f

圖1 新型算法的時間耗費(f=0.8)

從圖1可以看出，在實驗系數為0.8時，只有當問題規模近似增加至70時，新型算法的時間耗費才會有較為明顯的遞增，效率遠遠高于經典回溯算法。

表5列出了在不同的實驗系數和不同的問題規模下，新型算法得到問題最優解的時間耗費情況。從表5中可知，新型算法普遍隨實驗系數的增加而減少，其原因在于，隨著實驗系數的增加，背包的容量不斷增大，背包可以容納的物品數量相應增加，從而減少了回溯的概率，進而提高了算法效率。

表5 新型算法在不同實驗系數、不同問題規模下的時間耗費

4 結束語

0-1背包問題是經典的NP完全問題，而經典的回溯算法采用枚舉的思想，通過深度優先搜索解空間樹尋找問題的最優解。在問題規模較小時，回溯算法同其他求解0-1背包問題的經典算法相比，具有更小的時間耗費和空間耗費。但隨著問題規模的增加，回溯算法在時間和空間上都有極為明顯的增加，這種增加導致算法在較短時間內無法得到問題的最優解。

該文將貪心算法的高效性和經典回溯算法的最優性相結合，提出的融合貪心策略與剪枝策略的新型算法，將經典貪心算法得到的問題近似解用于剪枝策略的判斷條件中，減少了經典回溯算法遍歷過程中的無效搜索；同時，在進行物品選擇的判斷時，使用背包剩余容量作為約束條件，大大提高了算法的求解效率。大量仿真實驗結果表明，該新型算法在保證得到問題最優解的同時，有效提高了算法的運行效率。