基于Canny 算子的改進圖像邊緣檢測算法*

杜緒偉 陳 東 馬兆昆 劉方全

（1.青島科技大學機電工程學院 青島 266061）（2.中車青島四方機車車輛股份有限公司 青島 266111）

1 引言

視覺分揀的本質就是通過機器視覺來替代人眼來進行判斷和測量，圖像邊緣檢測作為數字圖像處理技術的重要組成部分，已廣泛應用于機器人、目標定位和視覺導航等領域［1］。在工業化中為了實現對工件的判斷，通常需要對工件進行邊緣檢測來獲取其具體信息。邊緣保存了圖像大量的重要信息，而且邊緣檢測也是最近機器視覺領域的重要課題，運用也越來越廣泛。傳統的邊緣檢測算法，如Sobel 算子［2］、Roberts 算子［3］、Prewitt 算子［4］、Kirsch 算子［5］等雖然實施起來比較方便，但是這些算子檢測的結果都達不到既定要求。Laplacian 算子［6］雖然在精度方面做出了很大的改進，但是對于噪聲還是比較敏感，因此在處理圖像的實際效果中并不明顯。John Canny［7］在1986年提出最佳邊緣檢測算子的三個準則并在此基礎上提出了Canny 算法，有效平衡了定位精度、最小響應、檢測時間的邊緣檢測最優標準。傳統的Canny 算法雖然被普遍的運用，但是算法在濾波部分采用傳統的高斯濾波來進行預處理，在清除噪聲的過程中會過度清除掉圖像的邊緣信息，造成部分邊緣信息丟失進而降低邊緣檢測的精度，而且固定的雙閾值也導致了該算法的適應性較差［8］。所以傳統的Canny算法還需要進一步的改進才能得到更好的運用。

2 傳統的Canny算法

2.1 圖像的高斯濾波說明

Canny 基于邊緣檢測提出了三個判斷準則［9］，而他也在此基礎上進一步發展創造出了Canny 算法。Canny 算法采用二維零均值高斯函數，并對圖像矩陣執行卷積運算，實現圖像的消除噪聲和平滑處理。選取的高斯函數的表達式為

2.2 圖像梯度計算

Canny算法采用2×2的模板來計算灰度圖像梯度［10］。通過其在X方向、Y方向的像素的一階導數，可以確定像素的梯度幅值。

2.3 傳統Canny算法的不足

雖然傳統的Canny 算法得到了廣泛的運用，但是其仍然存在很大的問題［11］。

1）基于2×2 的鄰域進行計算，對噪音比較敏感，而且容易丟失邊緣信息并且易檢測出大量干擾信息，影響檢測精度；

2）采用固定的雙閾值，致使算法處理邊緣分布不同的圖像時不能自主改變，適應性不強。

3 改進的Canny算法

傳統的Canny 算法在濾波部分采用高斯濾波來進行預處理，在清除噪聲的過程中會過度清除掉了圖像的邊緣信息，導致部分邊緣信息丟失［12］。針對這一問題本文運用雙邊濾波來代替高斯濾波進行圖像預處理，這樣不僅可以有效地去除噪聲還可以保留更多有用的邊緣信息。運用Ostu 法來進行閾值分割，而后融合形態學梯度思想進行Canny 算子邊緣檢測，來獲得邊緣圖像。

3.1 雙邊濾波

雙邊濾波［13］是Tomasi在1998 年提出的一種非線性濾波方法。它不僅可以保持邊緣信息還可以達到降噪平滑的效果。與高斯濾波相似，雙邊濾波對每個像素及其領域內的像素進行加權平均。雙邊濾波是兩個高斯濾波的結合：一個計算圖像空間鄰近度的權值［14］；另一個計算圖像像素值相似度的權值。雙邊濾波由空間權重與相似權重組成。

空間權重：與像素的位置有關系，為像素之間的距離，定義為

3.2 最大類間方差法

最大類間方差法將兩類的類間方差作為判別準則，即σ2的最大值便為最佳選擇的閾值T。

3.3 融合形態學梯度的邊緣提取

形態學一般表示生物學的一個分支，數學形態學便是從生物形態學發展而來。數學形態學作為從圖像中提取表達和描繪區域形狀的有用圖像分量的工具，是由一組形態學代數運算組成［16］。最基本的形態學算子有膨脹、腐蝕、開運算和閉運算四種。

一般二值圖像中的形態學：

作為Z2中的集合A和B，B對A的腐蝕定義為

運用這些算子或者組合可以進行圖象形狀和結構的分析及處理［19］。融合了形態學梯度思想，通過腐蝕和膨脹處理閾值分割后的圖像，而后將這兩幅二值圖像取差集，進而得到形態學梯度圖［20］。如圖1 所示形態學梯度處理不僅清除了圖像中的小的噪聲干擾，還可以填補物體中的空洞進而提高檢測精度。將差值圖像和原始濾波圖像求交集圖像便可以得到具有更精確邊緣的灰度圖。

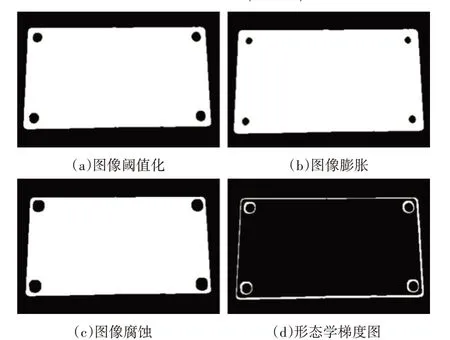
圖1 形態學處理

4 實驗與分析

為得到改進后的Canny 算法的效果，本文用Visual Studio2015 軟件利用C#語言編程配置0pencvsharp 在Windows 操作系統里進行驗證。分別用兩個不同零件進行實驗得到兩組實驗結果如圖2、圖3所示。

圖2 第一組實驗圖像

圖3 第二組實驗圖像

總體來說，本文所采用的改進的Canny 邊緣檢測算法與傳統的算法相比在清除噪聲和保留更多的邊緣信息上做的更突出。由于傳統的算法對于噪聲的比較敏感，造成圖像上會有各種干擾因素的出現，影響到邊緣信息的精確度進而導致檢測的結果不理想。而改進后的算法可以盡量避免噪聲并精確地得到最優化的邊緣信息。由于新算法只須要處理圖像中的一小部分區域，所以處理效率得到提升。

5 結語

邊緣檢測一直是視覺領域的研究熱點，研究方法也有很多。本文在研究傳統Canny 算法的基礎之上，對其噪聲干擾比較大、閾值適應性比較差等方面做出了改進。

1）通過利用雙邊濾波替代了高斯濾波，避免了高斯濾波使其即保持邊緣信息也可以達到降噪平滑的效果，增強了抑制噪聲能力。

2）利用最大類間方差法進行閾值分割，使目標和背景分離更加準確，減小了因背景因素影響而產生的誤差。

3）用融合形態學梯度來進一步使邊緣信息更加完善來改進Canny 算法，使圖像邊緣提取的精確度更高。