無刷直流電機的分數階建模方法*

吳雨林 李 眾

（江蘇科技大學 鎮江 212003）

1 引言

無刷直流電機的出現代替了許多傳統的電機，它是現代電力電子技術、控制理論和電機技術相結合的產物，具有優越的調速性能，主要表現在控制性能好、調速范圍寬、啟動轉矩大、運行平穩、效率高等方面。目前已經被廣泛用于諸多高精產業，如國防、航空航天、機器人、工業過程控制、精密機床、汽車電子、家用電器、智能汽車、辦公自動化等領域［1］。

分數階微積分中是近年來常用的一種數學方法，分數階系統是用分數階微分方程描述的系統［2］，其中的階數能夠連續變化，可以更準確地描述復雜系統。目前分數階微積分已被廣泛使用于各種領域的建模研究，如電池模型［3］、圖像處理［4］流體力學［5］、生物系統［6］等。在電機控制領域，電感和電容這些儲能元件本質上是分數階的，采用分數階微積分方法能夠實現對整個電動機系統建立模型。Rajagopal 等［7］從無刷直流電動機的整數階模型出發，推導了無刷直流電動機的分數階模型，對無刷直流電動機的動態特性和混沌控制和穩定進行了研究。余偉等［8］進行了永磁同步電機的分數階建模研究，該方法將電動機作為一個整體進行建模，未能很好地利用電動機的組成機理。鄭偉佳等［9］根據永磁同步電動機的組成機理分別對電磁環節和機械環節進行參數辨識，得到了更好的模擬效果，但是模型實用性較差，需要專門設計多個實驗對不同的模型參數進行辨識。本文將采用一種新的方法對無刷直流電機的系統特性進行分數階建模，以取得對電機更好的模擬效果。

2 無刷直流電機的分數階建模

2.1 無刷直流電機數學模型

無刷直流電機的數學模型可參考文獻［10］，這里給出本文所修改的分數階模型相關方程。無刷直流電機的電壓平衡方程式可表示為

其中分數階的階次滿足0＜ε＜2。

本文所用的無刷直流電機型號為57BL52-230，其參數如表1所示。控制板使用的是基于意法半導體公司、型號為STM32F302R8 的ARM芯片。

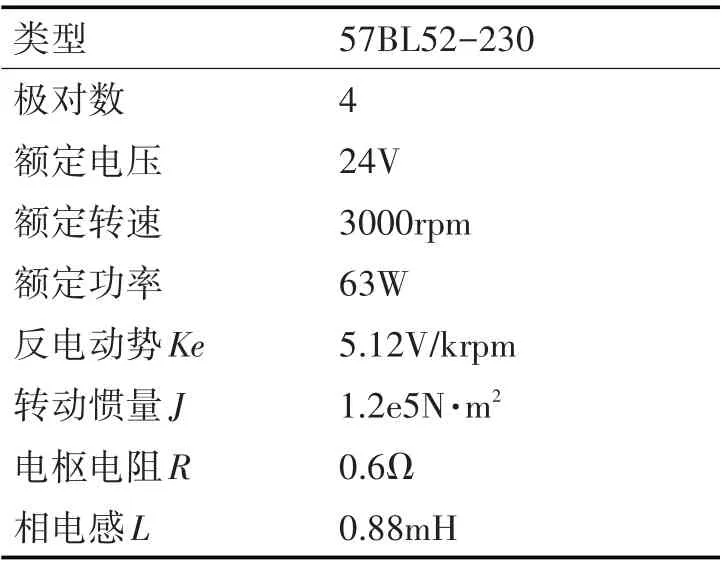
表1 物理樣機電機參數

2.2 控制策略

本文無刷直流電機采用的控制策略為基于矢量控制的雙閉環PI 控制。外環為速度控制，由速度期望值nref與其實際值n作差，速度控制器選用PI控制。內環為電流控制，定子電流經矢量變換被分解成直軸電流Id（勵磁電流）和交軸電流Iq（轉矩電流），電動機矢量控制就是控制轉矩電流和勵磁電流大小。由速度控制器得到Q 軸的期望電流Iqref，本文采取期望勵磁電流Idref=0 的控制策略，由期望矢量電流Iqref、Idref與實際值Id、Iq 作差，電流控制器選用PI 控制，得到直軸交軸的電壓值，再經矢量反變換，通過SVPWM（空間矢量脈寬調制）得到三相逆變器PWM波的占空比，最終控制電機。

整個控制流程如圖1所示。

圖1 控制流程框圖

3 分數階模型的參數辨識

3.1 分數階微積分算子的整數階近似

分數階積分器1/sη可用一個一階積分器和一個用Oustaloup 遞推濾波器近似的分數階微分器串聯來逼近［12～14］，設需要逼近的頻段范圍為（ωL，ωH），Oustaloup 遞推濾波器的個數為2N + 1（N 為正整數），則分數階積分環節可近似成如式（5）所示形式。

3.2 分數階階次的獲取

分數階參數辨識采用基于輸出誤差的非線性辨識方法［15］，對系統的分數階模型階次辨識的方法如下。

在實驗平臺和仿真模型上加上相同的激勵得到響應的實驗數據y仿真數據y?，詳細表現系統的誤差的公式為

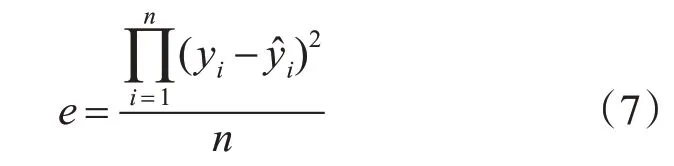
其中n 為采樣數據點個數，為了讓分數階模型能更準確地描述電機行為，需要得到系統誤差值為最小值時θ和ε的值，將此值作為分數階模型的階次參數此時對模型參數選取的問題轉變成求解數學模型取得誤差函數極小值時對應的參數問題。由于基于機理建立的仿真模型較為復雜不適用復雜的曲線擬合算法，并且參數變化范圍不大，同時為了避免陷入局部最優解，本文采用窮舉法劃區計算，最終得到分數階模型的參數。具體步驟如下。

1）搭建實驗平臺，根據已經測得的電機參數利用仿真軟件Matlab 建立相應的基于機理的無刷直流電機的整數階仿真模型和控制器模型，根據前文所述方式建立相應的分數階仿真模型。

2）在實驗平臺用階躍信號測試物理樣機，通過數據采集器得到電機的速度響應曲線，將實驗數據輸入Matlab，用高斯濾波對實驗數據進行降噪處理，由于是離散化地采樣，在Matlab 默認為是線性插值。濾波處理前后的圖形如圖2所示。

圖2 電機采樣數據處理

3）保持仿真模型的PI 控制器參數和實驗平臺的控制器參數一致，用同樣的信號測試無刷直流電機分數階仿真模型，調整θ、ε值，得到分數階無刷直流電機仿真模型的仿真結果。

4）用經濾波處理后得到的實驗數據和分數階無刷直流電機仿真得到的仿真數據計算系統誤差值，其結果如表2，未在表中顯示的θ、ε其計算系統誤差的結果均大于352。

表2 系統誤差值

由表2 可知，θ=0.76，ε=1.10 時，作為測量標準系統誤差e 的值最小，這時無刷直流電機分數階仿真模型階躍響應的轉速曲線對實際電機階躍響應的轉速曲線擬合得最好，因此本文模型選取θ=0.76、ε=1.10 作為無刷直流電機的分數階模型階次。分數階模型對實際電機轉速曲線的擬合效果如圖3。

圖3 轉速曲線擬合效果

4 無刷直流電機分數階模型驗證

為了判斷無刷直流電機的分數階模型是否比原來的整數階模型更準確地模擬了實際電機的行為，需要進一步實驗驗證。

設計實驗分別在不同的速度控制器參數下和不同的輸入激勵下，比較整數階模型的系統和分數階模型與實際電機的差距，結果如下。

1）更改速度控制器參數對仿真模型進行驗證，實際電機階躍響應的轉速曲線及整數階模型和分數階模型階躍響應的轉速曲線如圖4，其中整數階模型和分數階模型的系統誤差值e 的計算結果分別為532、8311。

圖4 更改控制器參數后模型的模擬效果

2）更改輸入激勵對仿真模型進行驗證，得到的實際電機階躍響應的轉速曲線及整數階模型和分數階模型階躍響應的轉速曲線如圖5。統誤差值e的計算結果分別為938、7495。

圖5 更改輸入激勵后模型的模擬效果

圖4、圖5 均可以明顯看出分數階模型比整數階模型對實際電機有更好的模擬效果。

5 結語

實際系統的復雜性，導致基于已知參數的機理建模的無刷直流電機模型對實際電機的模擬效果很差，而基于數理建模的無刷直流電機的模型則難以對電機仿真模型進行修改。本文提出的無刷直流電機的分數階建模方法兼具機理與數理建模的優點，且更具有實用性和可操作性。由辨識得到分數階模型的分數階階次，在不同的實驗條件下進行實驗并對分數階模型和整數階模型的仿真結果進行對比表明，分數階模型比整數階模型能更精確地模擬實際無刷直流電機的行為。