空調轉子壓縮機摩擦噪聲的有限元分析*

宋方濤 陳光雄 宋啟峰 楊布雷

(西南交通大學摩擦學研究所 四川成都 610031)

隨著空調的普及以及人們生活水平的提高，空調的噪聲問題越來越受到關注[1]。以往對于空調噪聲的研究多基于空調的氣動噪聲和電磁噪聲等方面開展，通過對采集到的噪聲信號進行頻譜分析或是對空調系統進行流體動力學仿真，確定噪聲源的位置及其傳遞路徑后，提出相應的改進方案以達到降低噪聲的目的。實際上，空調工作過程中的很大一部分噪聲是由壓縮機和風機等設備的異常振動引起，也就是所謂的機械噪聲；而在機械噪聲當中，由于摩擦振動而引起的噪聲的現象又普遍存在于各類機械裝備中[2-4]。

摩擦振動及其引起的噪聲問題是近年來學術界研究比較活躍的一個課題，主要針對摩擦系統產生摩擦噪聲的機制以及抑制摩擦噪聲的措施展開研究[5-7]。目前，關于摩擦噪聲的產生機制大概分為4類，即黏著-滑動機制、自鎖-滑動機制、摩擦力-相對滑動速度負斜率機制以及模態耦合機制[8-11]。從20世紀80年代至今，模態耦合理論逐漸被認為是最有可能引起摩擦噪聲的理論。ARONOV等[12]最早提出了摩擦噪聲發生的模態耦合機制，認為摩擦力會導致非對稱摩擦系統的剛度耦合，從而激發摩擦系統的不穩定振動，并向系統外輻射摩擦噪聲。LILES[13]首次將有限元法應用到制動摩擦噪聲的研究中，對制動摩擦系統進行了運動穩定性的復特征值分析，進而求解系統的不穩定振動模態。WAGNER等[14]的實驗數據表明，摩擦系統的不穩定振動頻率與復特征值方法計算得到的不穩定頻率基本一致，這說明了復特征值分析法的準確性。為探討空調轉子壓縮機摩擦噪聲的產生機制，本文作者提出了一種利用商業有限元軟件ABAQUS對空調壓縮機的相關摩擦副進行摩擦噪聲預測的方法，利用復特征值分析法對可能引起摩擦噪聲的頻率進行預測，并與實際測得的頻率進行比較，驗證了該方法在預測壓縮機摩擦噪聲頻率方面的有效性。

1 摩擦系統的復特征值分析

復特征值分析是一種計算結構復模態的方法，主要用于檢驗系統在頻域范圍內的穩定性，求解系統在一定條件下最容易發生不穩定振動的頻率及其對應的振動模態。

采用有限元法對摩擦系統的各個部件進行離散化，忽略系統阻尼的影響，得到系統的動力學方程：

(1)

假設摩擦系統接觸面間的摩擦因數為μ，接觸面間的法向力可以用線性彈簧來模擬，那么接觸面間的摩擦力可以表示為

Fff=kffu

(2)

式中：Fff、kff分別代表節點的摩擦力矢量和摩擦耦合剛度矩陣。

則引入摩擦力后系統的動力學方程以及該方程的特征方程為

(3)

(k-kff-λm)φ=0

(4)

式中：λ、φ代表方程(4)的特征值和特征向量。

由于引入摩擦力后系統的剛度矩陣k-kff為非對稱項，這使得特征方程(4)的特征值可能出現復數。那么方程(3)的通解可以寫為

u(t)=∑φiexp(αi+iωi)t

(5)

式中：φi代表特征方程(4)的特征矢量；αi、ωi分別代表特征值的實部和虛部。

對有n個節點自由度的有限元動力學系統，就有n個特征值和特征矢量。當系統的特征值實部為正時，根據式(5)可知此時系統會出現運動不穩定，即一個非常小的擾動就會使系統出現振幅愈來愈大的自激振動，從而向系統外輻射摩擦噪聲。

通常會根據特征值的實部和虛部構造新的參數來對系統的穩定性進行描述：

ξ=-αi/(π|ωi|)

(6)

參數ξ稱為摩擦系統的等效阻尼比，當特征值的實部為正數時，等效阻尼比為負數，此時系統可能出現不穩定振動；且等效阻尼比越小，系統的不穩定程度越大，就越容易產生摩擦噪聲。

2 轉子壓縮機摩擦系統模型

2.1 轉子壓縮機簡介

轉子壓縮機的歷史十分悠久，早在20世紀初就已經作為電冰箱用壓縮機而被大量使用。隨著精密加工技術的迅速發展，轉子壓縮機在技術方面已日臻完善，并廣泛應用于空調、電冰箱及小型商用制冷設備中[15]。

轉子壓縮機壓縮機構的基本構成如圖1所示，它由曲軸、氣缸體、上下法蘭、隔板以及內部的滾子、滑片等零件組成。如圖2所示，轉子壓縮機的滾子安裝在曲軸偏心部上，使得滾子的外表面與氣缸的內表面相切，于是在氣缸內表面與滾子外表面之間便形成一個月牙形的空間，其兩端被氣缸蓋密封著，構成壓縮機的工作腔。壓縮機中的滑片在背部彈簧力的作用下，緊緊壓在滾子的外表面，將月牙形空間分成吸氣腔和壓縮腔兩部分。壓縮機運轉時，吸氣腔和壓縮腔的容積周期變化，于是就實現了吸氣、壓縮、排氣等工作過程[15]。

2.2 摩擦系統有限元模型

選取轉子壓縮機中的曲軸與上下法蘭建立摩擦系統的有限元模型，在有限元分析軟件ABAQUS中對各部件進行離散化，并對接觸部分的網格進行局部細化，得到的有限元網格如圖3(a)所示，其中各部件的網格均采用C3D8I的網格類型。由于轉子壓縮機內部的壓縮機構與殼體焊接成一個整體，且文中討論的這款壓縮機采用上法蘭焊接在殼體上，氣缸體、隔板以及下法蘭等部件通過螺釘連接至上法蘭的固定方式。因此在為有限元模型施加邊界條件時，對上法蘭外緣與殼體接觸的部分采用鉸支約束，上法蘭、下法蘭與螺釘接觸的部分采用綁定約束；再對曲軸的位移自由度和轉動自由度進行約束，并在施加載荷的分析步中放開相應的位移自由度，使摩擦副表面能夠穩定接觸，如圖3(b)所示。

曲軸-法蘭摩擦系統中，主要存在曲軸-上法蘭、曲軸-下法蘭以及曲軸偏心部止推面-下法蘭3個摩擦副。在有限元模型中，將這些接觸對的切向接觸屬性設定為罰函數摩擦接觸，并分別為各個接觸對設定摩擦因數，而法向接觸屬性則設定為硬接觸，如圖4(a)所示。對于有限元模型中需要施加邊界條件的區域，在這些區域與相應的參考點間建立分布耦合的關系，并將邊界條件直接施加在參考點上，如圖4(b)所示。

轉子壓縮機曲軸-法蘭摩擦系統有限元模型的材料屬性如表1所示，其中上法蘭和下法蘭采用相同的材料加工而成，螺釘則選用標準件。

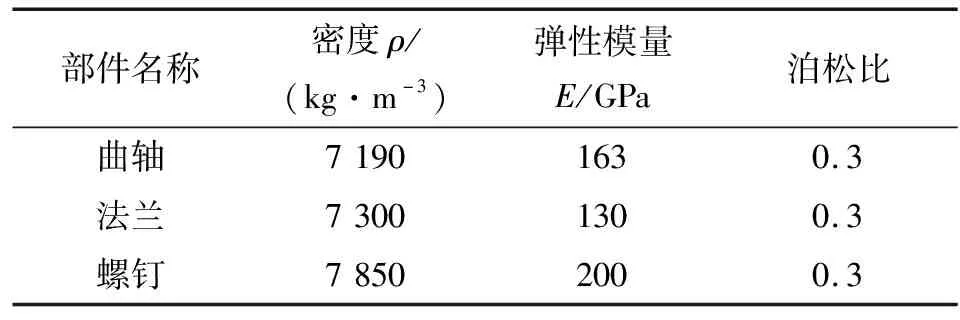
表1 摩擦副的材料屬性

2.3 模型預測頻率與實測頻率的對比

為了預測曲軸-法蘭系統可能發生摩擦噪聲的不穩定頻率，取曲軸和法蘭間的摩擦因數μ=0.3、0.4，利用有限元分析軟件ABAQUS對摩擦系統的不穩定頻率以及相應的等效阻尼比進行計算，得到摩擦系統不穩定頻率的分布情況分別如圖5、6所示。分別在壓縮機的中部和下部設置測點，對壓縮機運行頻率為80 Hz時產生的振動加速度信號進行采集，并對采集到的信號進行功率譜密度分析，結果如圖7所示。

由圖7(a)可知，μ=0.3時，下測點切向和法向加速度的功率譜密度均在頻率約7 200 Hz處存在一個峰值，且切向加速度在約7 200 Hz處對應的幅值最大。而從圖5可以看到，μ=0.3時，摩擦系統恰在頻率約7 200 Hz處存在一個不穩定頻率，且其等效阻尼比的絕對值最大，其模態振型如圖8(a)所示。那么可以認為摩擦噪聲發生時下測點處的法向振動和切向振動是耦合的，摩擦系統的模態耦合是引起摩擦噪聲的重要原因。

從圖6可以看到，增大摩擦因數到0.4后，摩擦系統產生不穩定振動的趨勢有所增強，且出現了頻率約為8 550 Hz的新的不穩定頻率，其模態振型如圖8(b)所示。而由圖7(b)可知，μ=0.4時，中測點的切向和法向加速度均在頻率約8 550 Hz處存在一個峰值，且切向加速度在約8 550 Hz處對應的幅值最大。這同樣說明了摩擦噪聲發生時，摩擦系統發生了模態耦合。

通過上面的對比可以看到，雖然利用有限元方法提取到的摩擦系統不穩定頻率與實測振動信號的分析結果間存在微小的誤差，但這些誤差都在允許的范圍內，即可以認為有限元模型的計算結果與實測數據的分析結果有很好的一致性。另外也可以看到，摩擦噪聲發生時，摩擦系統的法向振動和切向振動發生了耦合，使得系統的振動幅值增大。

3 結果及分析

3.1 摩擦因數對摩擦噪聲的影響

摩擦因數對摩擦噪聲的發生有重要的影響[7]。有限元仿真結果顯示，曲軸-法蘭摩擦系統隨著摩擦因數的變化，發生摩擦噪聲的模態主要集中在第13階以及第15階。圖9顯示了摩擦因數對第13階模態特征值實部的影響。可以看到，當摩擦因數較小時，系統復特征值的實部都小于或等于0，即沒有摩擦噪聲；而當摩擦因數大于某一個值時，系統復特征值的實部都為正值，且隨著摩擦因數的增大，特征值的實部也在不斷增大，表明系統出現了摩擦噪聲，并且噪聲的強度在不斷增加。

圖10顯示了摩擦因數對第15階模態特征值實部的影響，可以看到其變化規律與第13階模態相似，但它們特征值的實部開始出現正值時的摩擦因數有所不同。可以認為特征值實部開始為正值時的狀態就是系統發生摩擦噪聲的臨界狀態，而此時的摩擦因數就是系統的臨界摩擦因數。

因為某階模態特征值的虛部在每次計算中變化很小，由等效阻尼比的定義可知，隨著摩擦因數的增加，不穩定模態等效阻尼比的絕對值會不斷增大，即系統產生摩擦噪聲的趨勢會越來越強。

3.2 摩擦噪聲發生時系統的模態耦合

曲軸-法蘭摩擦系統第2階至第16階模態的頻率隨摩擦因數的變化情況如圖11所示。可知，當曲軸和法蘭間的摩擦因數μ≥0.3時，摩擦系統的第12階和第13階模態在頻率約7 200 Hz處發生了耦合，簡記為mode(12,13)；隨著摩擦因數的增大，當曲軸和法蘭間的摩擦因數μ≥0.4時，摩擦系統的第14階和第15階模態在頻率約8 550 Hz處也發生了耦合，簡記為mode(14，15)。可以看到，系統在摩擦噪聲的臨界摩擦因數處發生了模態耦合，再次證明了模態耦合是導致系統摩擦噪聲的重要原因。

3.3 法蘭的彈性模量對摩擦噪聲的影響

楊偉茂等[16]在對壓縮機轉子系統進行模態分析時發現，在一定范圍內，適當增大軸承的支承剛度，可以較大程度地提高轉子的臨界轉速。由該研究結果猜想，壓縮機法蘭剛度的變化會對曲軸-法蘭摩擦系統的不穩定振動產生一定的影響。

文中通過改變法蘭的彈性模量來研究法蘭剛度對摩擦系統不穩定振動的影響。已知初始法蘭材料的彈性模量為E0=130 GPa，將有限元模型中法蘭的彈性模量依次更改為0.6E0、0.7E0、1.1E0、1.2E0和1.3E0后再進行計算，分析法蘭的彈性模量變化后摩擦系統的不穩定振動特性。

圖12所示為摩擦系統第13階模態等效阻尼比的絕對值隨法蘭彈性模量的變化情況。可知，隨著法蘭彈性模量的增加，不穩定模態的負阻尼比的絕對值在不斷增大，但增加到E0后其增速逐漸放緩。由前面關于等效阻尼比的定義可以得出結論：增大法蘭的彈性模量后，摩擦系統的穩定性有所降低，即法蘭的彈性模量越高，越容易激發系統的不穩定振動，就越容易產生摩擦噪聲。

4 結論

(1)曲軸-法蘭摩擦系統中摩擦力的引入將在摩擦系統的剛度矩陣產生非對稱項，使系統具有發生模態耦合的可能性，進而產生不穩定的振動與噪聲。

(2)摩擦因數的變化對摩擦噪聲的產生具有關鍵性的作用，提高摩擦系統的臨界摩擦因數可以在一定程度上提高系統的穩定性。

(3)當發生摩擦噪聲時，摩擦系統某2個自然振動頻率會互相重合，即系統發生模態耦合，此時系統的復特征值實部會出現正值。

(4)法蘭的彈性模量對摩擦噪聲的產生有重要影響，當法蘭的彈性模量取較高的數值時，摩擦系統就越容易產生摩擦噪聲。