基于帶抑制弧的Petri網表示的嵌入式系統模型的子網化簡

張 瑋 夏傳良

(山東建筑大學計算機科學與技術學院 山東 濟南 250101)

0 引 言

嵌入式系統在無人機、物聯網和醫療設備等領域都有廣泛應用。對可靠性、正確性和實時性的高要求是嵌入式系統的特征[1-2]。為了保證系統的正確性和有效性，需要在嵌入式系統的設計中采用形式化的建模方法。

目前可用于描述嵌入式系統的模型主要有有限狀態機、數據流圖、Petri網[3]和SysML(Systems Modeling Language)。基于Petri網表示的嵌入式系統PRES+模型是一種用于嵌入式系統建模、驗證和分析的比較有效的方法[4-8]。

為了設計嵌入式系統，Cortés等[4]提出了一種基于PRES+的嵌入式系統的形式化計算模型。Karlsson等[5]提出了一種PRES+與基于組件的系統級設計集成的方法。Xia等[7-8]提出了PRES+模型的細化方法和合成方法。

加入抑制弧可以增強Petri網的建模能力[9-10]。為了提高PRES+的建模和驗證能力，我們在PRES+模型中加入抑制弧，得到基于帶抑制弧的Petri網表示的嵌入式系統(PIRES+)模型。但是，在PIRES+建模和驗證復雜的嵌入式系統過程中存在狀態空間爆炸問題。

為了解決Petri網的狀態空間爆炸問題，國內外學者提出了多種模型轉換方法，其中化簡操作是一種重要的轉換方法。

Boucheneb等[11]提出了一種時間Petri網(TPN)的部分化簡技術。Berthomieu等[12]給出了一種減少庫所和變遷數量的方法。對于PRES+系統，Xia[6]提出了化簡規則，在一定條件下，化簡后得到的PRES+與原模型完全等價。

本文的主要動機是給出PIRES+保性化簡規則，使得化簡前后保持可達性、功能性和實時性等性質不變，不用進行可達空間分析，從而達到緩解狀態空間爆炸的目的。

1 相關概念

定義1PRES+模型N=(P,T,FI,FO,M0)，其中：P={p1,p2,…,pm}是庫所的有限非空集合；T={t1,t2,…,tm}是變遷的有限非空集合；FI?P×T是一組輸入弧的有限非空集合，定義了庫所到變遷的輸入關系流；FO?T×P是一組輸出弧的有限非空集合，定義了變遷到庫所的輸出關系流；M0是N的初始標記。托肯攜帶了時間和數據信息。對于每一個變遷，都存在與之相關的變遷函數、最小變遷時延和最大變遷時延。

將抑制弧加入PRES+模型中，得到PIRES+模型。

定義2PIRES+模型N={P,T,FI,FO,I,M0}，其中：P={p1,p2,…,pm}是庫所的有限非空集合；T={t1,t2,…,tm}是變遷的有限非空集合；FI?P×T是一組輸入弧的有限非空集合，定義了庫所到變遷的輸入關系流；FO?T×P是一組輸出弧的有限非空集合，定義了變遷到庫所的輸出關系流；I?P×T(I∩F=?)是抑制弧的有限非空集合；M0：P→N0是N的初始標記，其托肯攜帶了時間和數據信息。

k=是托肯，其中:v是托肯的類型標識；r是托肯的時間標識。

只有當抑制庫所為空時，被抑制的變遷才會被觸發。在圖形上，抑制弧將庫所連接到變遷，并且弧在變遷處以空圓環結束。其余約束與PRES+模型的約束相同。

以下給出兩個PIRES+模型具有相同可達性、功能性和實時性的概念。

定義3兩個PIRES+模型N1和N2若有相同的可達性需滿足：

(1)N1和N2有相同數量的輸入庫所和輸出庫所。

(2) 若把相同數目的托肯數放入N1和N2的輸入庫所中，那么N1和N2的相應輸出庫所得到的托肯數相同。

定義4兩個PIRES+模型N1和N2若有相同的功能性需滿足：

(1)N1和N2有相同的可達性。

(2) 若把具有相同類型標識的托肯放入N1和N2的輸入庫所中，那么N1和N2的相應輸出庫所得到的托肯的類型標識也相同。

定義5兩個PIRES+模型N1和N2若有相同的實時性需滿足：

(1)N1和N2有相同的可達性。

(2) 若把具有相同時間標識的托肯放入N1和N2的輸入庫所中，那么N1和N2的相應輸出庫所得到的托肯的時間標識也相同。

2 化簡規則

2.1 基于T型子網的化簡規則

在PIRES+模型中，基于T型子網化簡規則(RST)的前提條件是存在一個T型子網滿足定義6。示例見圖1，T型子網部分被化簡為變遷t。

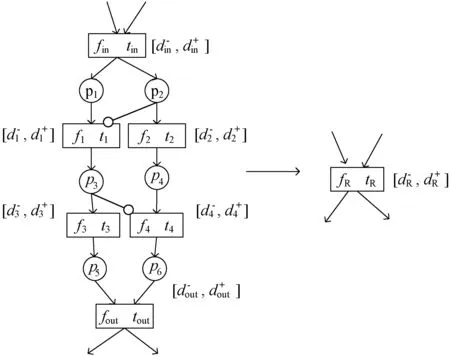
圖1 化簡規則RST示例

定義6若PIRES+模型NR={PR,TR,FIR,FOR,IR,MR,0}是模型N={P,T,FI,FO,I,M0}的子網，需滿足以下條件：

(1)PR?P,TR?T,PR≠?,TR≠?。

(2)FIR=FI∩{(PR×TR)|(PR×TR)?I),FOR=FO∩(TR×PR),IR=I∩{(PR×TR)|(PR×TR)∈I}。

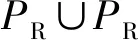
(4) {tin,tout}?TR,tin是NR的唯一輸入變遷，tout是NR的唯一輸出變遷。

(5) 對于?t∈TR,存在變遷函數f:τ(p1)×τ(p2)×…×τ(pn)→(q),·t={p1,p2,…,pn},q∈t。

(6) 對于?t∈TR,存在最小變遷時延d-和最大變遷時延d+,兩者均為非負實數且滿足d-≤d+。

(7) 子網中的抑制弧不會造成網的死鎖。

(8) 同一組庫所和變遷不能同時存在有向弧和抑制弧。

定義7對于PIRES+模型NR={PR,TR,FIR,FOR,IR,MR,0}的變遷集TR-{tin,tout}存在變遷函數fR。對于TR-{tin,tout}，?fR：τ(p1)×(p2)×…×τ(pn)→τ(q)，其中:(TR-{tin,tout})={p1,p2,…,pn};q∈(TR-{tin,tout})。

以圖1為例，因為變遷t1和變遷t3是串聯關系，變遷t2和變遷t4是串聯關系，t1與t2、t3與t4又分別是并聯關系，所以fs=(f1°f3)‖(f2°f4)(符號° 表示復合操作，符號‖表示并列操作)。

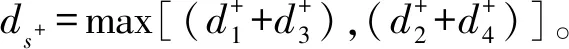
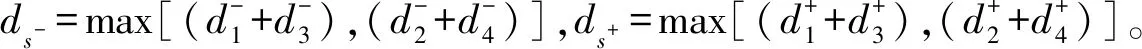
假設1假設PIRES+模型的T型子網NR={PR,TR,FIR,FOR,IR,MR,0}滿足：

(1) 在一個執行過程中(托肯從tin流入通過NR再從tout流出)，如果tin被觸發則tout也會被觸發。

(2) 對于PR，如果在初始狀態下無托肯，則在執行過程后也不含托肯。

(3) 在tin被觸發前和tout被觸發后，?t∈TR-{tin,tout}，t不處于使能狀態。

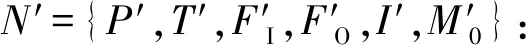
(1)P′=P-PR。

(2)T′=T-TR+{t}。

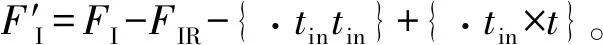
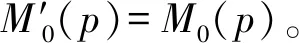
(6)fR=fout°fs°fin。

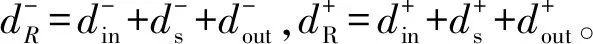
(8)I′=I-IR。

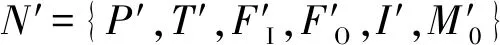
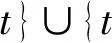
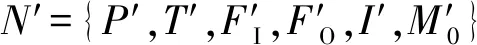
因為N′-N1=N-N2,所以N′和N有相同的可達性、功能性和實時性。

2.2 基于P型子網的化簡規則

在PIRES+模型中，基于P型子網化簡規則(RSP)的前提條件是存在一個P型子網滿足定義10。示例見圖2，P型子網部分被化簡為庫所p。

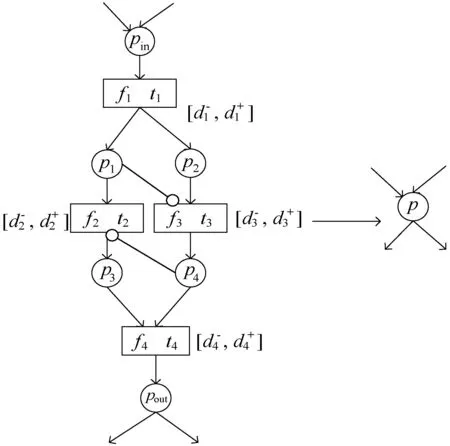
圖2 化簡規則RSP示例

定義10若PIRES+模型NR={PR,TR,FIR,FOR,IR,MR,0}是PIRES+模型N={P,T,FI,FO,I,M0}的P型子網，需滿足：

(1)PR?P,TR?T,PR≠?,TR≠?。

(2)FIR=FI∩{(PR×TR)|(PR×TR)?I),FOR=FO∩(TR×PR),IR=I∩{(PR×TR)|(PR×TR)∈I)。

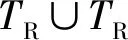
(4) {pin,pout}?PR,pin是NR的唯一輸入庫所，pout是NR的唯一輸出庫所。

(5) 對于?t∈TR,存在變遷函數f:τ(p1)×τ(p2)×…×τ(pn)→τ(q),·t={p1,p2,…,pn},q∈t·。

(6) 對于?t∈TR,存在最小變遷時延d-和最大變遷時延d+，兩者均為非負實數且滿足d-≤d+。

(7) 子網中的抑制弧不會造成網的死鎖。

(8) 同一組庫所和變遷不能同時存在有向弧和抑制弧。

定義11對于PIRES+模型NR={PR,TR,FIR,FOR,IR,MR,0}的變遷集TR存在變遷函數fR。對于TR，?fR：τ(p1)×τ(p2)×…×τ(pn)→τ(q)，其中:·TR={p1,p2,…,pn};q∈TR·。

以圖2為例，因為變遷t1和變遷t3、t2是串聯關系，變遷t4和變遷t3、t2是串聯關系，t3與t2又分別是并聯關系，所以fs=f1° (f3‖f2)°f4。

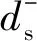
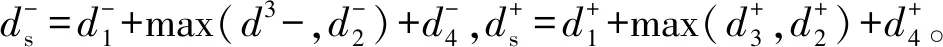
假設2假設PIRES+模型的P型子網NR={PR,TR,FIR,FOR,IR,MR,0}滿足：

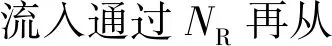
(2)PR如果在初始狀態下無托肯，則在執行過程后也不含托肯。

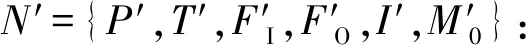
(1)P′=P-PR+{p}。

(2)T′=T-TR。

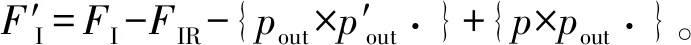
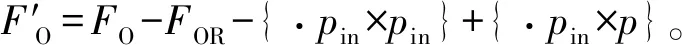
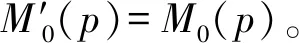
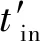
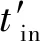
(8)I′=I-IR。

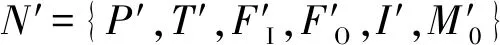
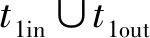
因為N-N1=N′-N2,所以N′和N有相同的可達性、功能性和實時性。

3 應用實例

本節以一個基于手機通信模型的簡化實例來說明PIRES+模型化簡規則的有效性。

系統初始化后，首先進行終端和鍵盤的初始化，然后打印無線通信菜單，通過創建鍵盤控制子程序完成手機號的撥入與撥出。該系統的PIRES+模型如圖3所示。

圖3 基于嵌入式的手機通信模型

在該模型中，各變遷的含義為：t1表示系統初始化；t2表示終端初始化；t3表示鍵盤初始化；t4表示打印無信通信菜單；t51表示接受鍵盤輸入；t52表示控制命令判斷；t53表示無效信息輸入；t54表示撥入號碼；t55表示撥出號碼；t56表示系統循環等待；t61表示檢測是否停止；t62表示停止；t63表示未停止；t7表示返回。

該PIRES+模型中虛線所標注部分為T型子網N1，使用基于T型子網的化簡規則RST進行化簡得到初步化簡模型N′，結果如圖4所示。

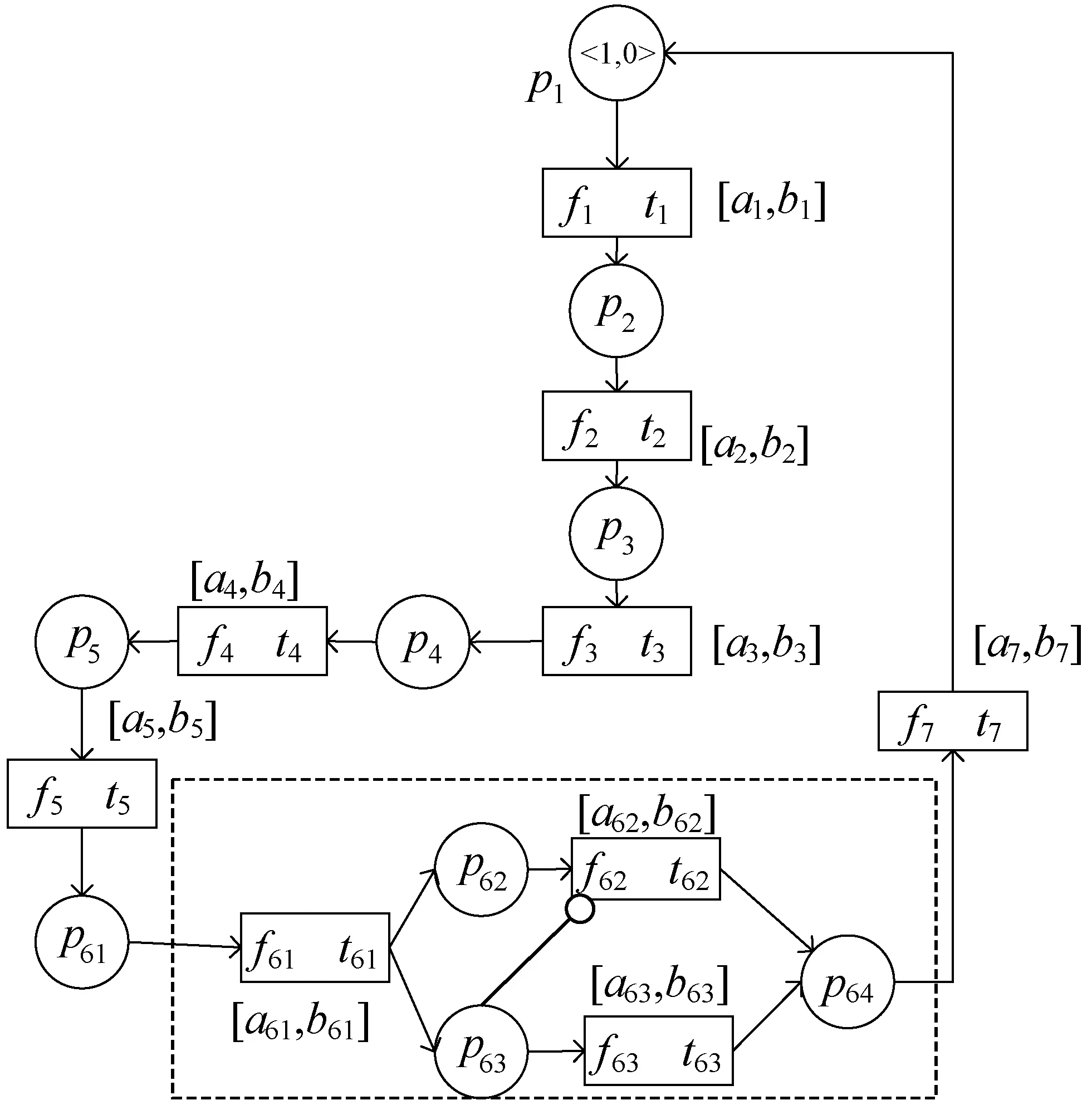
圖4 使用RST規則后的化簡結果

圖4中，f5=f51° ((f52° (f54‖f55))‖f53)°f56,a5=a51+max(a52+max(a54,a55),a53)+a56,b5=b51+max(b52+max(b54,b55),b53)+b56。根據定理1得，所得的初步簡化模型N′與原模型有相同的可達性、功能性和實時性。

對于模型N′，虛線所標注部分為P型子網N2。使用基于P型子網的化簡規則RSP進行化簡，得到模型N″(如圖5所示)。

圖5 使用RSP規則后的化簡結果

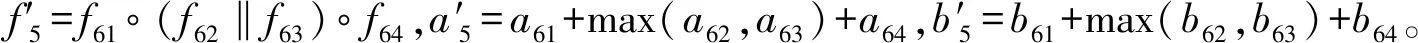
對于模型N″，虛線所標注部分可用基于T型子網的化簡，得到最終的簡化模型Nr(如圖6所示)。

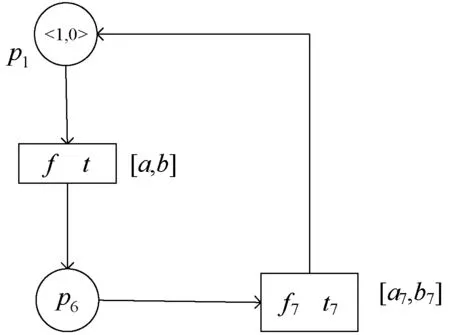
圖6 最終化簡結果

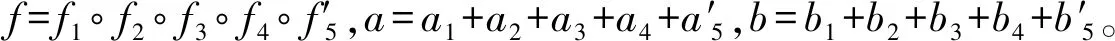
綜上所述，最終得到的模型Nr與原模型N有相同的可達性、功能性和實時性。

4 結 語

本文在PRES+的基礎上加入抑制弧，得到PIRES+模型。PIRES+模型增強了建模能力，但是在建模和分析過程中存在狀態空間爆炸問題。為了緩解此問題。本文提出PIRES+的兩種化簡規則，并且證明了化簡后所得模型與原模型有相同的可達性、功能性和實時性。本文的實例說明了該化簡規則的有效性。