釓單晶磁化曲線的微磁學模擬

陳志斌，曹永軍

（內蒙古師范大學 物理與電子信息學院，內蒙古 呼和浩特 010022）

釓（Gd）是唯一在室溫下具有磁性的稀土元素，是一種典型的海森堡模型鐵磁體，也是具有代表性的經典磁制冷鐵磁材料［1］。在過去的幾十年中，HCP 結構的Gd 得到了廣泛關注，大量應用于實驗和理論研究，特別是在電子結構和有限溫度磁性能方面，Gd 元素的許多基態性質都得到很好解釋［2］。基于Landau-Lifshitz（L-L）方程的微磁方法［3］，可以求解典型鐵磁材料和器件的磁矩運動，但是這些計算中，不能解釋在有限溫度下的熱傳導效應，故而引入了一種原子尺度的有效自旋哈密頓量在稀土元素中，由于Gd3+離子的純s 態性質，導致了相對較低的磁晶各向異性［4］，所以Gd 占有突出的地位。針對釓這種對溫度很敏感的材料，研究其內部參數與溫度的關系是非常重要的。同時，釓是很好的合金元素，在耐熱鎂合金中，由于釓元素的加入可提高其高溫強度和抗蠕變性能［5］。開發含Gd 的合金也是一個重要的研究方向。

因為Gd 具有室溫磁性轉變點，本文應用混合蒙特卡羅微磁學方法，研究了Gd 單晶在室溫附近磁化強度隨外場和溫度的變化規律，得到磁化曲線。通過Gd 單晶的變化規律可以對不同溫度下的Gd 單晶各向異性常數、交換作用系數進行研究。混合蒙特卡羅微磁學方法的應用，對后續類似Gd 單晶的其它鐵磁性物質的研究具有指導意義。

1 混合蒙特卡羅微磁學方法

混合蒙特卡羅（HMC）方法是基于經典牛頓力學的運動方程通過積分求解而來的方法，目的是產生exp(-S[x])的類玻爾茲曼（Boltzmann）分布［6］。求解的常規路徑是首先設定特定的場景與該場景下的初始狀態，根據哈密頓方程產生與時間相關的連續狀態，隨著狀態的不斷改變，可以逐步實現平穩態附近的漲落并靠近穩態，但它受限于計算機的計算能力和其他因素，包含“時間”被拆分成離散的序列。這里“時間”可以是真實的時間也可以是虛擬的。

HMC 方法在低溫下求解硬磁材料的磁滯回線與L-L 方程的微磁學相近，但對于軟磁材料的計算，HMC 方法得到的磁滯回線相較于L-L 方程更為準確［7］。因為L-L 方程在矯頑力附近超過一半的磁矩為反平行亞穩態，而HMC 微磁學由于直接到達能量最小而無此情況。此外，大規模計算方面HMC 微磁學較L-L 方程微磁學快很多，HMC 微磁學在回線計算的每個外場下計算耗時均勻，而L-L 方程在矯頑力附近耗時較多。當微磁學格子數超過1 000 時，HMC 方法計算速度正比于格子數，計算速度遠超L-L 微磁學的速度。

1.1 HMC 微磁學算法的迭代過程

1.2 程序中重要參數

參數迭代步數Nstep對HMC 微磁學模擬結果有重要影響。在微磁學領域應用時［9］，迭代步數Nstep有所不同。迭代步數Nstep和蒙特卡羅時間δτ兩者相互制約，兩者的變化影響著HMC 算法的接受率，共同影響著算法的準確性。此外，迭代步數的取值影響著程序運行的時間。

在HMC 算法中，單個軌道中的“蛙跳”的迭代步數Nstep通常是10。對于HMC 的微磁學模型中，單個軌道的“蛙跳”的迭代步數Nstep需要進一步研究，這里設置為200。在HMC 算法中，蒙特卡羅時間通常被分成若干個軌道，每個軌道的長度為τ0=Nstepδτ，軌道數量為Ntrajectory，所以迭代步數取值需要同時兼顧算法的準確性和計算效率。

通過計算得到釓低溫下的磁化曲線，先找到釓單晶HCP 密排六方的模型（見圖1），其中晶胞參數［10］a=b=363.6 pm，c=578.26 pm，α=β=90°，γ=120°。每個原子有12 個近鄰（即Z=12），自旋S=是第一、二個電子歸一化的自旋算符。在鐵晶體中，由自旋波實驗獲得的Je/KBTC是0.22，而根據如下方程計算得到的結果是0.093（S=1，Z=8）或0.25（S=1/2，Z=8）。

圖1 釓原子HCP 模型Fig.1 HCP model of gadolinium

在HMC 算法中，蒙特卡羅時間τ是虛構的時間，而哈密頓量中的磁性系統自由能F[M]/(kBT)有多個波峰和波谷。磁性系統的自由能需要克服眾多能量勢壘從而達到亞穩態或者穩態。磁晶各項異性能加限制勢能可表示為

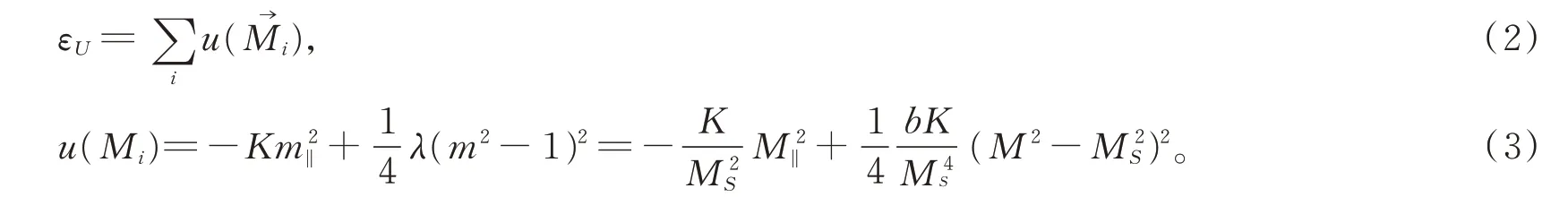
其中：m=為拉格朗日項，這一項將能量束縛在M=MS(T)附近漲落；M4是朗道二級相變中的雙勢阱。參數λ=bK，其中b是無量綱常數，當λ→∞時，可回到傳統微磁學中磁矩歸一化情形。

2 模擬結果

Gd 在室溫下是順磁性的，課題組利用上述原子尺度蒙特卡羅微磁學方法，編制程序模擬計算得到了Gd 的飽和磁化強度，用以研究飽和磁化強度隨外場和溫度的變化關系。其中Gd 晶體的HMC 哈密頓量包含兩項［11］，原子自旋共軛動量的動能項和原子自旋的標度自由能項。

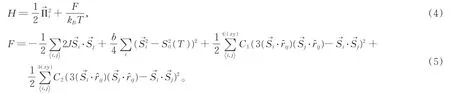
在確保系統保持鐵磁相的前提下，為了在約束勢中固定輸入各向同性交換常數J和S0(T)，不同溫度情況下的模擬計算MS(T)/MS(0)值及誤差大小見表1，并與文獻［1］中的實驗值進行比較，如圖2 所示。由表1 和圖2 可知，模擬值與實驗值基本吻合，隨溫度的變化趨勢也相同，Gd 單晶的飽和磁化強度隨著溫度增加而減小。

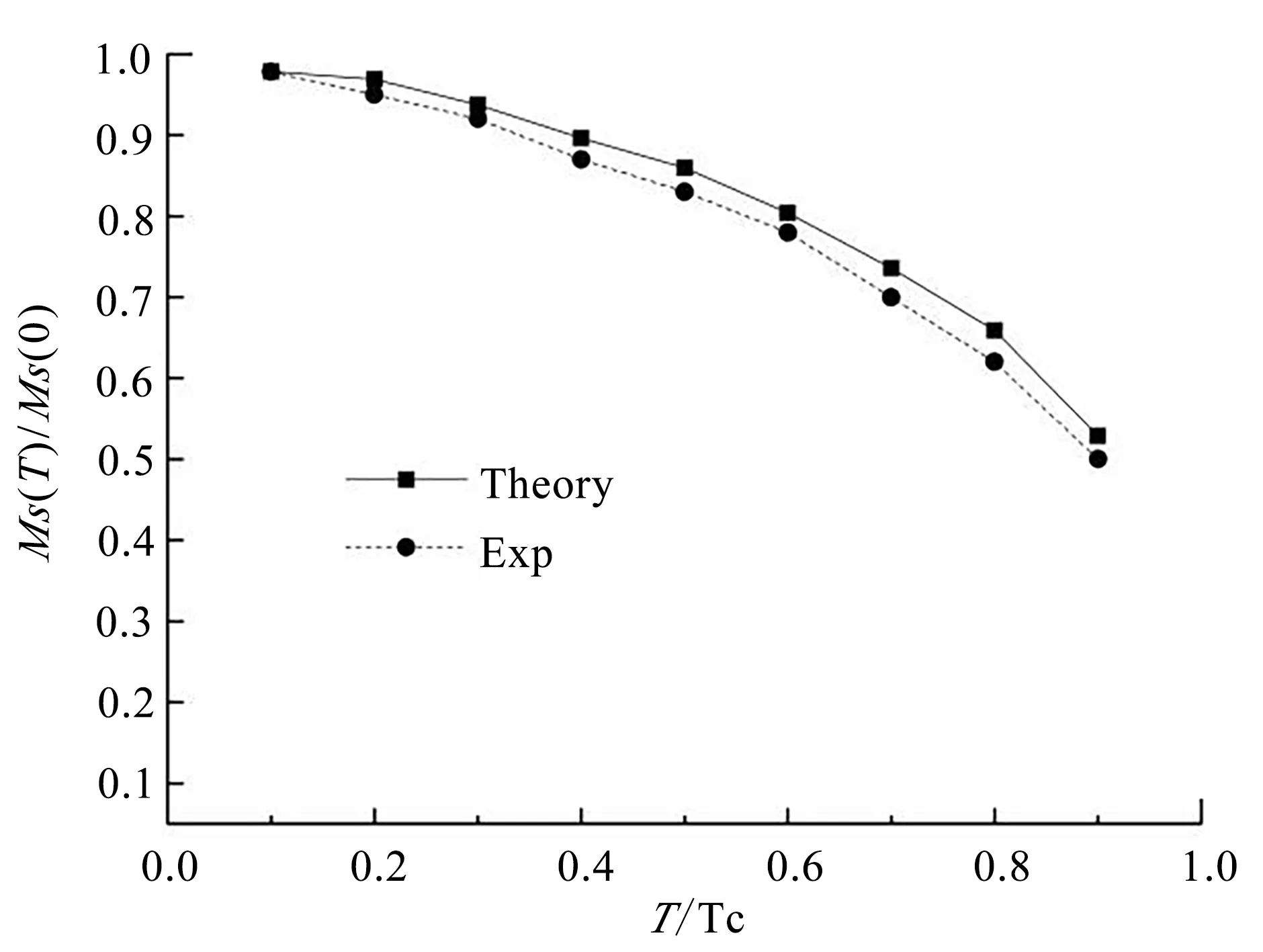
圖2 MS（T）/MS（0）隨溫度的變化規律Fig.2 Variation of MS（T）/MS（0）with temperature

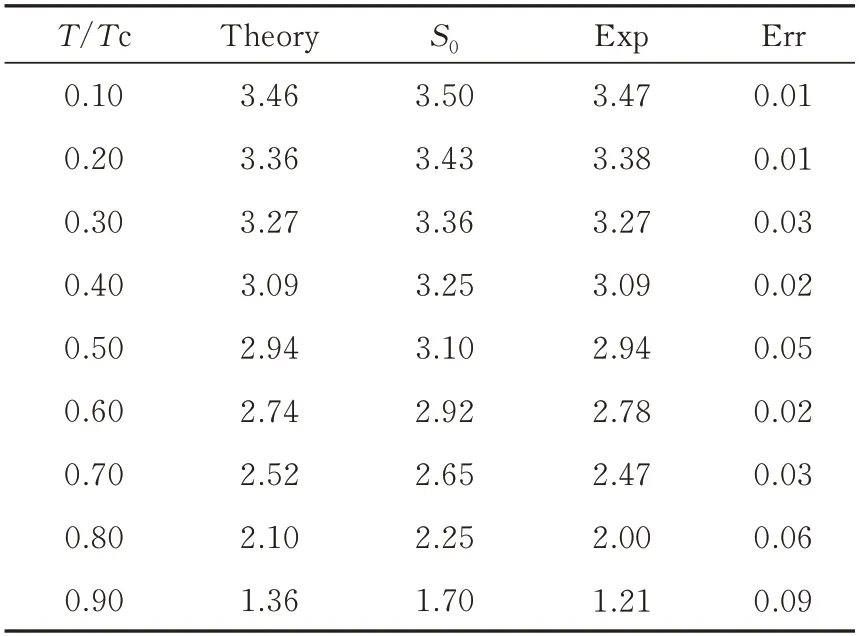
表1 不同相關溫度比值下的理論值與實驗值以及誤差大小Tab.1 Theoretical and experimental values and error size under different relative temperature ratios

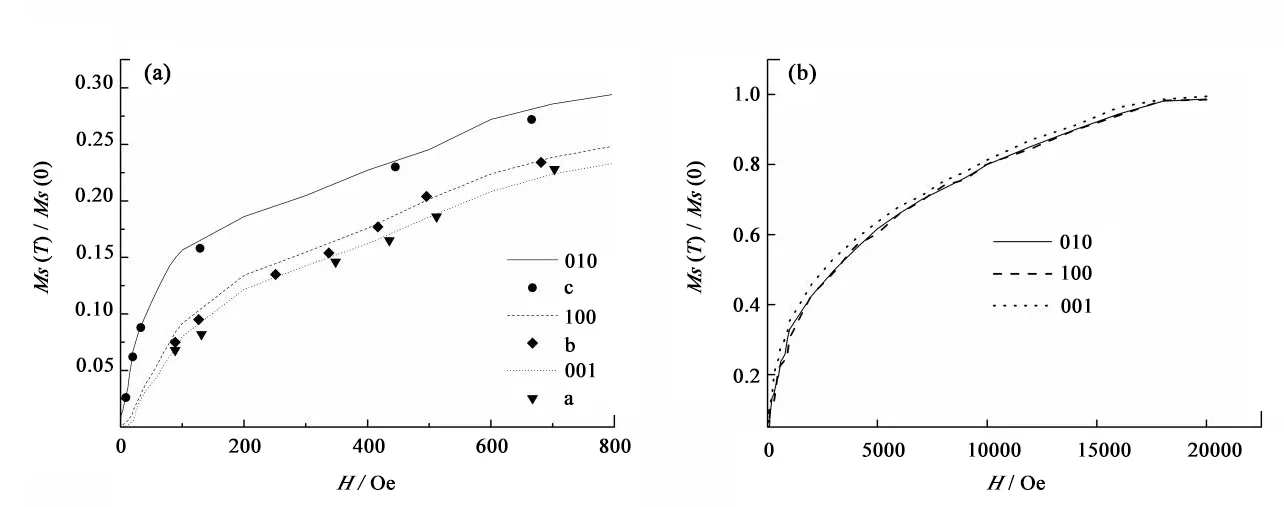
圖3 MS（T）/MS（0）隨著外場（H）變化規律Fig.3 The variation of MS（T）/MS（0）with external field

3 結論

本文使用原子尺度的有效自旋哈密頓量，以及混合蒙特卡羅方法得到Gd 單晶的磁化曲線，通過調節不同參數，找到接受度范圍在0.7～0.9 的結果，并分別對主要參數astar，Mwarm，Nstep，dt進行調試，找到與理論相近的實驗參數。通過得到磁化曲線，可以清楚地知道飽和磁化強度隨著外場和溫度的明顯變化，這為以后對類似釓的鐵磁性物質和其它順磁等磁性物質的研究奠定了一定的理論基礎。