混合指數型積分算子在Orlicz 空間中的飽和性
2022-03-18 08:10:52王家瑋吳嘎日迪
內蒙古師范大學學報(自然科學漢文版) 2022年2期
王家瑋,吳嘎日迪,2
(1.內蒙古師范大學 數學科學學院,內蒙古 呼和浩特 010022;2.內蒙古自治區應用數學中心,內蒙古 呼和浩特 010022)
0 引言
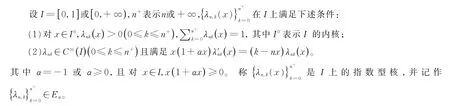
經文獻[1]計算可知
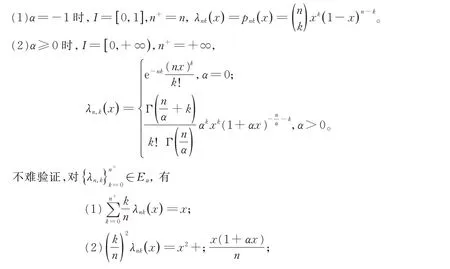

關于Tn在Lp空間內的飽和性問題已有一些研究,目前尚未見到在Orlicz 空間里研究這類算子的飽和性問題。本文借助Hardy-Littlewood 極大函數,凸函數的Jensen 不等式研究了該算子在Orlicz 空間內的飽和定理。
本文C表示與f,n,k無關的正常數,且在不同處取不同的值。
1 相關引理
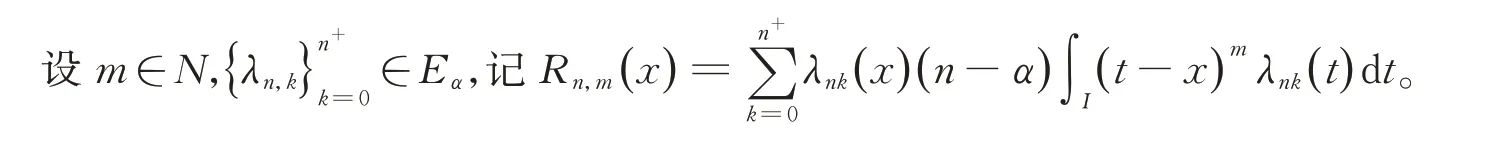
引理1[1]m∈N,x∈I,有

證明由Taylor 展開式
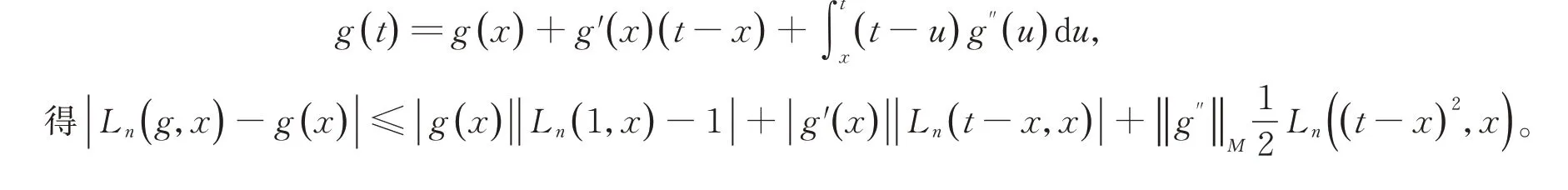
因此可得
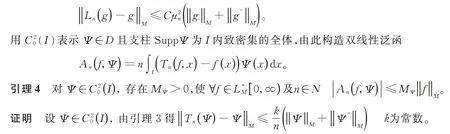
于是
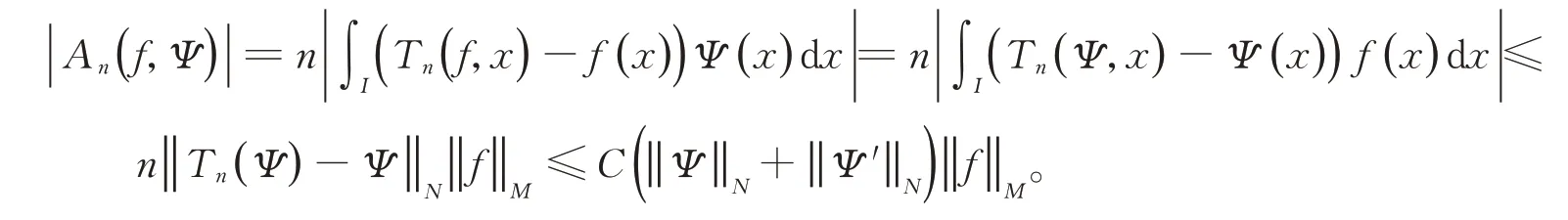
記φ(x)=x(1+αx)。
引理5[3-4]對每個g∈D,則
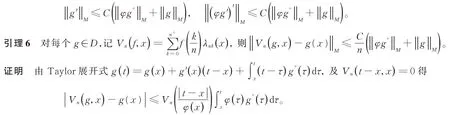
由Hardy-Littlewood 極大函數可得,M(x)為極大函數。
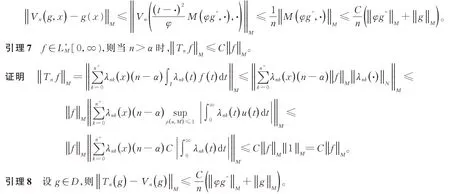
證明由文獻[1]
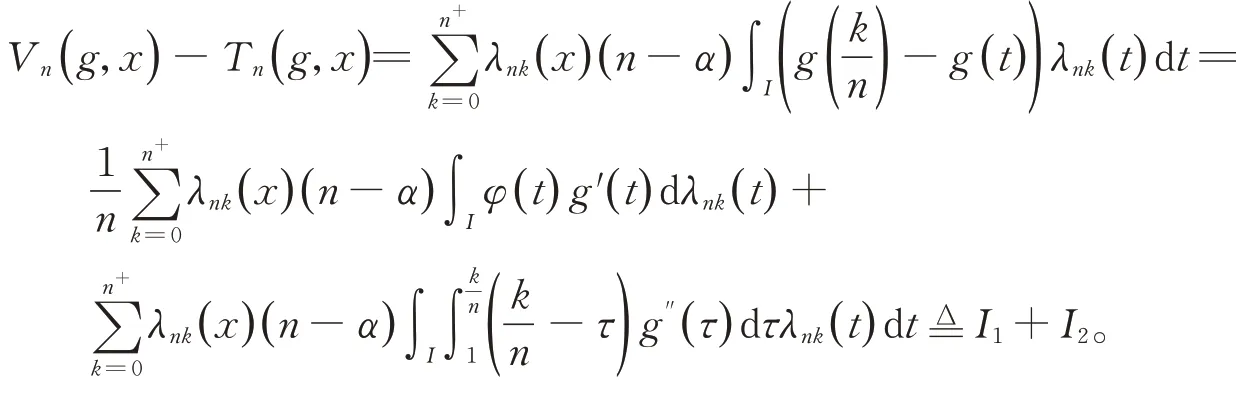
由引理5
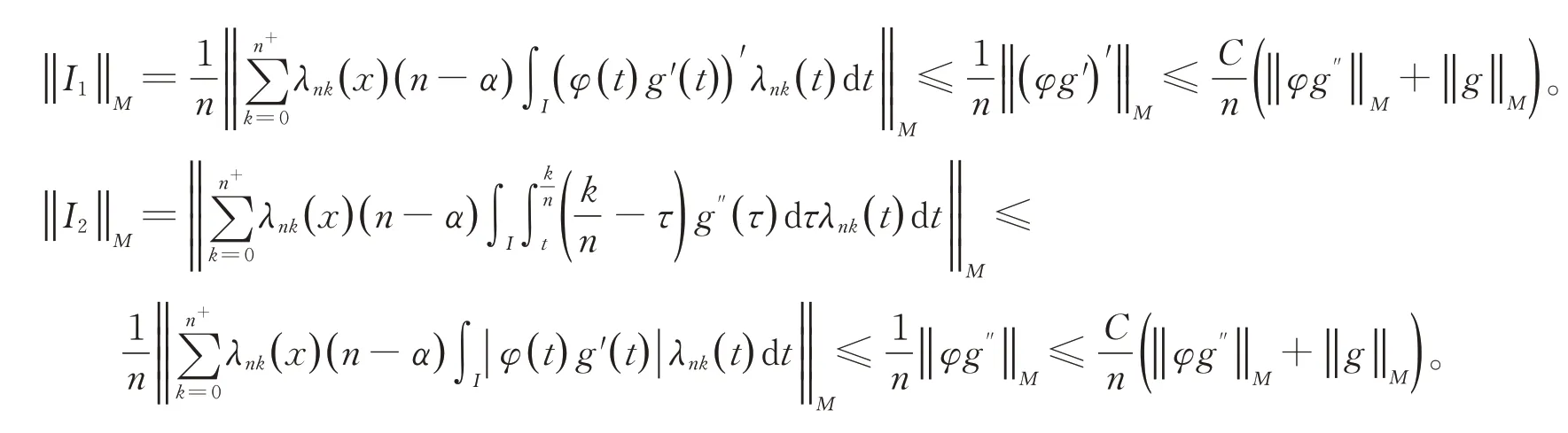
由引理6 及引理8 可得引理9。
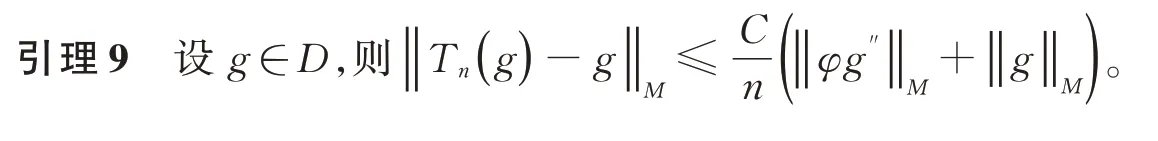
2 定理及證明

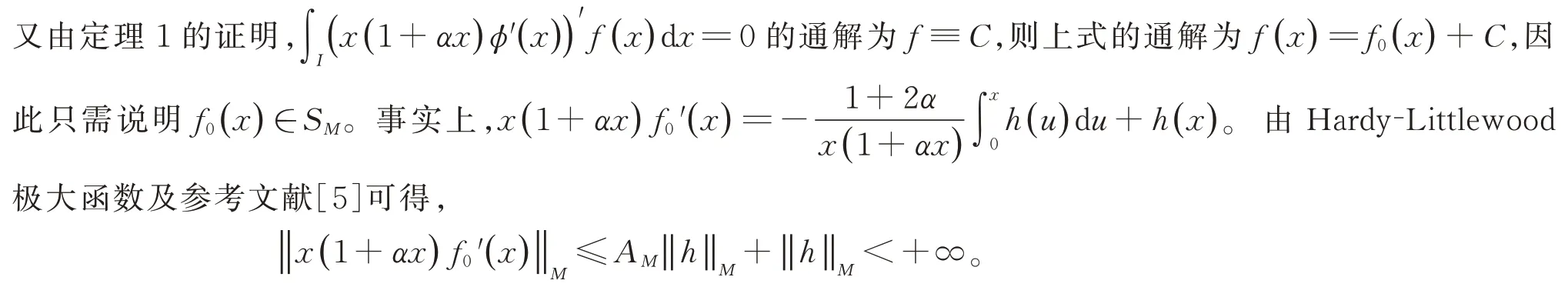
由引理9 和定理2 得到飽和定理(定理3)。
定理3
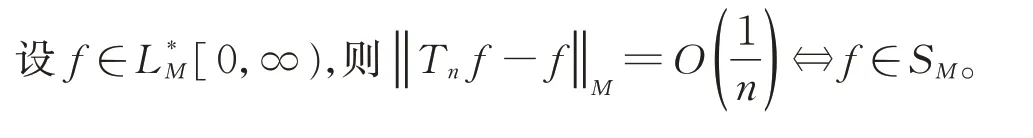
猜你喜歡
體育科技文獻通報(2022年3期)2022-05-23 13:46:54
天津外國語大學學報(2021年3期)2021-08-13 08:32:18
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
科技傳播(2019年22期)2020-01-14 03:06:54
學苑創造·A版(2019年5期)2019-06-17 01:14:21
民用飛機設計與研究(2019年4期)2019-05-21 07:21:24
汽車工程學報(2017年2期)2017-07-05 08:13:02
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21