電磁感應中的“知三求三”
■重慶市高新區教師進修學院 楊天才(特級教師,正高級教師)
恒力作用下的導體桿做切割磁感線運動,已知條件一般有:①基本屬性:導體桿的質量m,電路中的總電阻R;②外部環境:勻強磁場的磁感應強度B;③幾何長度:導體桿的有效切割長度L;④初始條件:導體桿的初速度為零;⑤隱含條件:導軌的電阻忽略不計,且足夠長。待求的物理量一般有六個:①恒定外力F;②導體桿的速度v;③導體桿的運動時間t;④導體桿的位移x;⑤產生的焦耳熱Q;⑥通過導體桿橫截面的電荷量q。如果知道這六個物理量中的三個,那么就可以利用方程Ft+ (-qBL)=mv,Fx+求剩下的三個。
說明:①若導體桿的初速度不為零,則同理可以“知三求三”;②若導體桿最終達到最大速度vmax,增加一個方程,則可以“知二求四”;③在沒有外力作用的情形下,方程Ft+(-qBL)=mv變為qBL=mv,則不能求解時間t,而位移x、焦耳熱Q、電荷量q仍可求。
例1如圖1所示,在豎直向下的磁感應強度為B的勻強磁場中,兩根足夠長的平行光滑金屬軌道MN、PQ固定在水平面內,相距為L。一質量為m的導體棒cd垂直于軌道MN、PQ放置,與軌道接觸良好。軌道和導體棒的電阻均不計。若軌道左端M、P間接一阻值為R的電阻,導體棒cd在拉力F的作用下由靜止開始運動,經過時間t,導體棒cd的速度為v。求:
(1)通過導體棒cd某一橫截面的電荷量q。
(2)時間t內導體棒cd的位移x。
(3)時間t內回路中產生的焦耳熱Q。
解析:(1)導體棒cd在拉力F和安培力的作用下做變加速直線運動,根據動量定理得qBL,解得。
(3)根據動能定理得Fx+(-Q)=,解得。
點評:恒力作用下的導體桿切割磁感線運動模型,涉及的物理量多,已知條件也多,所要用到的物理規律涵蓋高中物理的絕大多數,如力和運動的關系(受力分析、牛頓運動定律等),功和能的關系(動能定理、能量守恒定律等),沖量和動量的關系(動量定理、力的沖量等),電路(串并聯電路規律、閉合電路歐姆定律等),電磁感應現象(法拉第電磁感應定律、楞次定律、右手定則、左手定則等),因而成為了高考考查的重點、難點和熱點。本題已知恒定外力F、導體棒cd的運動時間t和速度v,屬于“知三求三”的具體應用。
例2如圖2所示,相距為L的兩根足夠長平行光滑金屬導軌MN、PQ與水平面間的夾角為θ,導軌上端N、Q間接有阻值為R的電阻。整個裝置處于磁感應強度為B的勻強磁場中,磁場方向垂直于導軌平面向下。將質量為m,阻值也為R的金屬桿cd垂直放置在導軌上,由靜止釋放,下滑距離為x時達到最大速度。重力加速度為g,導軌電阻不計,金屬桿cd與導軌始終接觸良好。求:

圖2
(1)金屬桿cd下滑過程中的最大加速度amax。
(2)金屬桿cd能夠達到的最大速度vmax。
(3)金屬桿cd由靜止運動至達到最大速度的過程中,金屬桿cd中產生的焦耳熱Q。
(4)金屬桿cd由靜止運動至達到最大速度的過程中,通過金屬桿cd某一橫截面的電荷量q。
(5)金屬桿cd由靜止運動至達到最大速度的過程所用的時間t。
(6)畫出金屬桿cd在下滑過程中的大致v-t圖像。
解析:(1)設金屬桿cd下滑到某位置時的速度為v,則金屬桿cd切割磁感線產生的感應電動勢E=BLv,回路中的感應電流I=,金屬桿cd受到的安培力F安=BIL,根據牛頓第二定律得,即。當v=0時,金屬桿cd的加速度最大,最大加速度amax=gsinθ,方向沿導軌所在平面向下。
(2)當金屬桿cd的加速度a=0時,速度最大,最大速度,方向沿導軌所在平面向下。
(3)根據能量守恒定律得mgxsinθ=,解得Q=。
(4)通過金屬桿cd某一橫截面的電荷量。
(5)根據動量定理得mgtsinθ-qBL=mvmax,解得。
(6)由(1)問的分析可知,金屬桿cd在下滑過程中的大致v-t圖像如圖3所示。
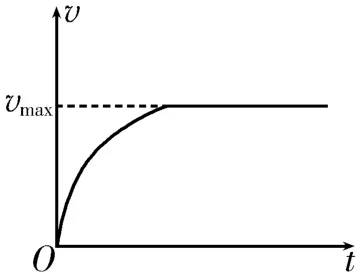
圖3
點評:本題已知恒定外力mgsinθ和金屬桿cd沿導軌下滑的位移x,還已知下滑過程中金屬桿cd最終達到最大速度,屬于“知二求四”的具體應用。

如圖4所示,相距為L的兩根平行光滑金屬導軌固定在水平面內,導軌左端接有阻值為R的電阻,磁感應強度為B的勻強磁場豎直向下分布在導軌所在空間內,質量為m的金屬棒PQ垂直于導軌放置。現使金屬棒PQ以一定的初速度v0向右運動,當其到達虛線c所在位置時停止運動,設導軌與金屬棒PQ的電阻均不計,求:
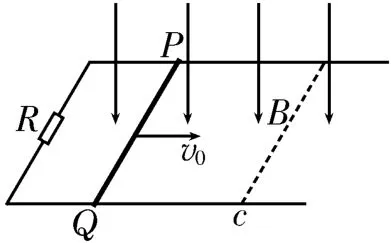
圖4
(1)通過金屬棒PQ某一橫截面的電荷量q。
(2)金屬棒PQ運動的距離x。
(3)電路中產生的焦耳熱Q。
參考答案:(1);(2);(3)。

