基于BP神經網絡的外圓磨削顫振在線識別和監測方法

朱歡歡，李厚佳，張夢夢，譚紹東，遲玉倫

（1.上海工程技術大學高等職業技術學院，上海 200437）

（2.上海市高級技工學校 制造工程系，上海 200437）

（3.上海理工大學 機械工程學院，上海 200093）

磨削是一種在精度要求較高時去除工件表面材料的機械加工方法，而顫振是磨削過程中影響加工質量的關鍵因素[1]。工件的幾何誤差、尺寸誤差、表面粗糙度等指標的惡化都可能是顫振所導致[2]。顫振的產生不可控，且機理復雜，從根源上對其分析有一定的盲目性和局限性[2]。因此，針對外圓磨削顫振現象進行在線監測及識別，做出工藝調整[1]，對改善工件表面質量、提高加工效率具有重要意義。

近年來，國內外學者對顫振監測做了許多研究，并通過“脫機操作”對工件表面進行光學測量來提高效率。于駿一等[3]在切削顫振發生之前對顫振進行了預報。孔繁森等[4]利用模糊數學原理將理論信號與試驗數據做貼合度分析進而進行了顫振識別。錢士才等[5]通過支持向量機對顫振進行了識別。這些方法有一定的效果，但是傳感器信號太單一，數據、特征參數少。呂長飛等[6]通過幅值法和小波分析實現了顫振的預測，但是小波分析局限于信號低頻部分，而且沒有深入考慮算法模型與數據適配問題，對結果的準確性影響較大。

KULJANIC 等[7]利用神經網絡對多顫振特征進行了信息融合、學習訓練和分類識別。為研究在磨削加工的復雜條件下的加工顫振現象，利用能夠以任意精度逼近非線性連續函數的BP 神經網絡模型，實現從輸入到輸出的映射，特別適用于求解這種內部機制復雜的問題。多傳感器作用下的BP 神經網絡模型也擁有高度自學習和自適應的能力，在對機床磨削顫振進行在線監測和識別時，主要通過對高頻聲發射傳感器信號、三向振動傳感器采集到的原始信號進行時域特征參數和小波包特征參數的提取，建立多樣本數據庫，對算法模型進行反復訓練得出識別結果，實現對機床磨削顫振現象的在線監測及識別。

1 顫振機理與監測

金屬加工過程中的振動分為強迫振動和自激振動[8]。強迫振動是受到的系統外周期性的擾動。刀具和工件在加工過程沒有周期性外力作用也會產生強烈的相對振動，該振動稱為自激振動，也稱顫振[9]。

再生型顫振是自激振動的一種，幾乎在所有的機床加工中都有發生。其產生機理是由于上次切削所形成的振紋與本次切削的振動位移之間產生了一定的相位差，動態切削厚度發生變化。當厚度達到一定程度時，就會發生再生型顫振。

如圖1所示，當連續2 次磨削產生振紋的相位差ε為0 或2π 時，動態切削厚度都不會發生變化；當相位差為π 時，動態切削厚度變化到最大值，顫振也最嚴重。由于振源來自機床內部，即使嚴格選取工藝參數，也不能完全避免發生顫振，最好的方法就是對其進行監測識別。

圖1 動態切削厚度產生示意圖Fig.1 Dynamic cutting thickness generation diagram

監測系統主要通過傳感器來采集振動、聲音等原始信號，對信號進行特征提取再利用算法判別狀態，其框架如圖2所示。

圖2 狀態監測框架Fig.2 Condition monitoring framework

監測系統對于采集信號的傳感器帶寬、安放位置也有著嚴格的要求。傳感器帶寬要能準確覆蓋顫振頻率。安放位置原則上是必須離振源足夠近才能采集到優質的信號。

2 特征參數預處理

2.1 相關分析

原始信號的預處理是信號分析的前提[10]。功率、振動和AE(acoustic emission)等傳感器在采集中被廣泛應用，但各類傳感器有利有弊：功率傳感器靈敏度較低反應不夠迅速；振動傳感器信號強度易受外界影響；AE 傳感器更是會受到周圍噪聲干擾。所以，采用單一的傳感信號進行監測難免會有弊端，試驗使用的是多種傳感器監測相結合，能夠很好地彌補監測信號單一的缺點。

2.2 時域特征參數

對原始數據進行時域分析時，首先對信號波形、幅值和周期性進行初步判斷，其次利用公式進行分析，常見的參數有極差、方差、標準差等。表1是有關時域特征參數的計算公式。

表1 時域特征參數計算公式Tab.1 Calculation formula of time domain characteristic parameter

2.3 小波包分解

原始信號通過分解得到低頻和高頻分量，高頻分量中含有大量的信號細節可以通過小波包提取。通常對原始信號進行3 層小波包變換[11]，信號被分配到8 個節點中，其分解結構如圖3所示。

圖3 小波包變換示意圖Fig.3 Wavelet packet transform diagram

若原始信號被分解到第j層（j=1,2,3···n），采樣率為f，頻帶總數為 2j個，第i個頻帶范圍為～分解層數越多，信號處理越精細。

每個節點系數中存儲的能量稱為小波包節點能量，表達式為：

其中：fji(t)和Eij分 別是第j層第i個節點的小波系數和該系數的能量值。各系數能量值與總能量的比值為

當顫振發生時，某個節點的能量值會驟增，因此能量占比很適合作為輸入型特征參數用到一些算法模型中。

3 BP 神經網絡結構

3.1 基本原理

采用3 層BP 神經網絡[12]對外圓磨床顫振在線識別。選擇三向振動、AE 傳感器信號作為原始信號，BP神經網絡輸入層神經元數目設為n個 (n=6)。根據Kolmogorov 定理，綜合考慮泛化學習能力，確定隱含層神經元數目k(k=2n+ 1，k=13)。BP 神經網絡結構如圖4所示。

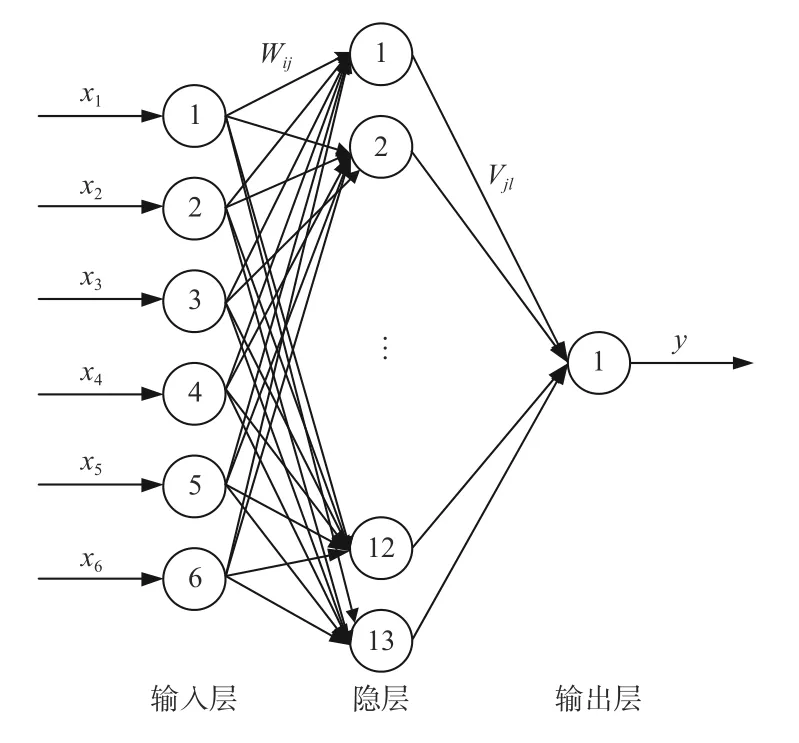
圖4 BP 神經網絡結構Fig.4 BP neural network structure

BP 神經網絡算法學習規則如下：表現函數沿著下降最快梯度方向，并不斷修正權值閾值：

其中：gk為 表現函數的梯度；ak為學習速率；xk為權值閾值。在BP 神經網絡中，輸入節點為xn，隱層節點的輸出為Zk，輸出節點為ym

試驗中的輸入節點數共6 個，隱層節點數13 個，輸出節點數1 個。其中輸入層與隱層間的網絡權值為wij（i=1,2···n,j=1,2···k），閾值為 θj；隱層節點與輸出節點之間的網絡權值為vjl，閾值為 θl（l=1,2···m, m為輸出節點的數量）設定好期望后模型的計算公式如下：

隱層節點的輸出

輸出節點的輸出

輸出節點的誤差

3.2 訓練過程

在BP 神經網絡迭代算法中選擇的是泛化精確度高的Levenberg-Marquardt 函數，隱藏層選擇的是雙曲正切S 型傳遞函數（tansig），輸出層選擇的是線性傳輸函數（purelin），訓練函數和自適應學習函數分別是默認的trainlm 和learngdm 函數。

BP 神經網絡的自適應學習能力很強。通過發射傳感器信號，對振動傳感器信號進行特征處理并建立樣本庫。設定迭代精度和目標期望，利用迭代函數開始訓練學習，不斷地輸出結果。如果輸出結果與期望值相比超出設置精度，則反向傳播。通過輸出層不斷逼近期望值，得到最優的BP 神經網絡模型，其過程如圖5所示。

圖5 BP 神經網絡訓練過程Fig.5 BP neural network training process

4 試驗設計和信號特征值提取

4.1 試驗設計

利用高頻AE、三向振動傳感器進行信號采集，外圓磨床型號為M1432BX1500；砂輪直徑為400 mm，磨削速度為35 m/s，磨削方式為外圓磨削，修整方式為金剛石筆修整(修整比為0.7)，加工工件為普通軸承，工件材料為標準軸承鋼。利用傳感器底座的強磁特性，將AE 傳感器吸附在尾架頂尖上，三向振動傳感器吸附在機床尾架上，試驗現場圖如圖6所示。

圖6 試驗現場圖Fig.6 Experiment site map

傳感器信號經過處理后輸出到采集卡，并顯示到PC端通過采集軟件進行下步分析，總的測試流程如圖7所示。

圖7 試驗測試流程簡圖Fig.7 Experimental test flow diagram

當磨削過程有顫振時，信號會發生變化，信號的時域、頻域都能提供相應的信息。在試驗中利用了AE傳感器采集，所以可以通過小波包分解求出各頻段的能量占比作為特征參數。

4.2 傳感器信號采集及分解

砂輪轉速和工件軸轉速分別為53 m/s 和110 r/min，保持不變，控制機床電機處于低速和高速2 種狀態。對AE 傳感器采集的原始信號進行小波包分解。采用db4 小波分解得到與頻段相對應的8 個節點，頻段間隔為62.5 kHz，頻段為0～500 kHz。低速與高速下高頻AE 信號的各頻段能量占比圖分別如圖8、圖9所示：

圖8 低速加工AE 信號能量占比Fig.8 Low-speed processing AE signal energy ratio

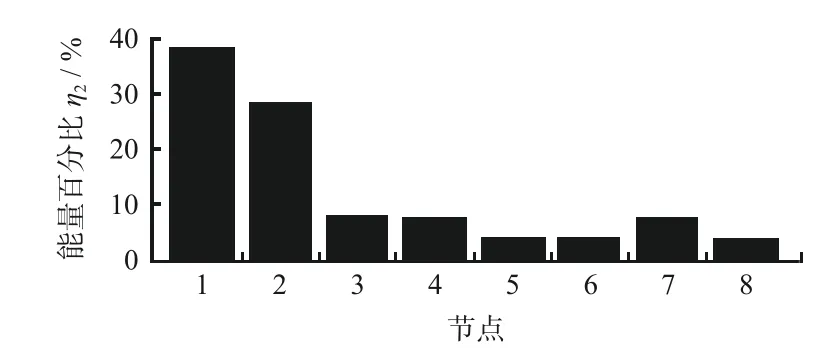
圖9 高速加工AE 信號能量占比Fig.9 High-speed processing AE signal energy ratio

將機床電機低速與高速2 種狀態下人小波包能量占比數據匯于表2中。由表2可知：低速和高速2 種狀態對比下，前3 個節點處能量占比變化顯著，后續節點中變化不明顯，可以推出顫振發生頻率集中在前3 個節點處的信號頻率部分。

表2 工件磨削AE 頻譜能量分布占比Tab.2 AE spectrum energy distribution occupation of workpiece grinding

機床尾架處的振動時域信號由三向振動傳感器采集，圖10、圖11、圖12分別是x方向振動時域信號圖、y方向振動時域信號圖和z方向振動時域信號圖，x方向的振動幅值主要在-0.04～0.06 V 范圍內變化，y方向振動幅值主要在1.92～2.04 V 范圍內變化，z方向振動幅值主要在-0.02～0.10 V 范圍內變化。可以看出在機床尾架處，與尾架x方向振動和尾架z方向振動相比，尾架y方向振動幅值變化更大，更易誘發磨削顫振現象的發生。

圖10 x 方向振動傳感器信號Fig.10 x-direction vibration sensor signal

圖11 y 方向振動傳感器信號Fig.11 y-direction vibration sensor signal

圖12 z 方向振動傳感器信號Fig.12 z-direction vibration sensor signal

4.3 信號特征值提取

已知BP 神經網絡模型輸出結果僅為有無顫振現象，將有無顫振現象賦值為{1，2}的集合對應監測的顫振結果。對傳感器信號進行特征值提取，建立樣本數據庫。不同現象下的各信號值不同，主要是通過對聲發射傳感器采集到的原始信號進行小波包分解，并取與顫振現象發生頻率接近的前3 個節點處的能量占比作為聲發射傳感器的信號特征值，對振動傳感器采集到的原始信號進行時域處理，選取x方向振動的均方根、y方向振動的偏態系數，z方向振動的標準差作為振動特征參數繼而建立信號特征樣本數據庫。表3為高頻采樣下電機高速運轉時聲發射小波包能量占比數據。表4為高頻采樣下電機低速運轉時的聲發射小波包能量占比數據。表5為三向振動信號特征值數據，前80 組是發生顫振時的振動特征值，后80 組是無顫振時的振動特征值。通過對正常磨削和發生顫振現象時的信號特征值計算得到表3、表4、表5的樣本數據庫，利用樣本數據庫結合BP 神經網絡模型可以對顫振現象進行監測及識別。

表3 高頻聲發射小波包能量占比（高速）Tab.3 High frequency acoustic emission wavelet packet energy ratio (high speed)

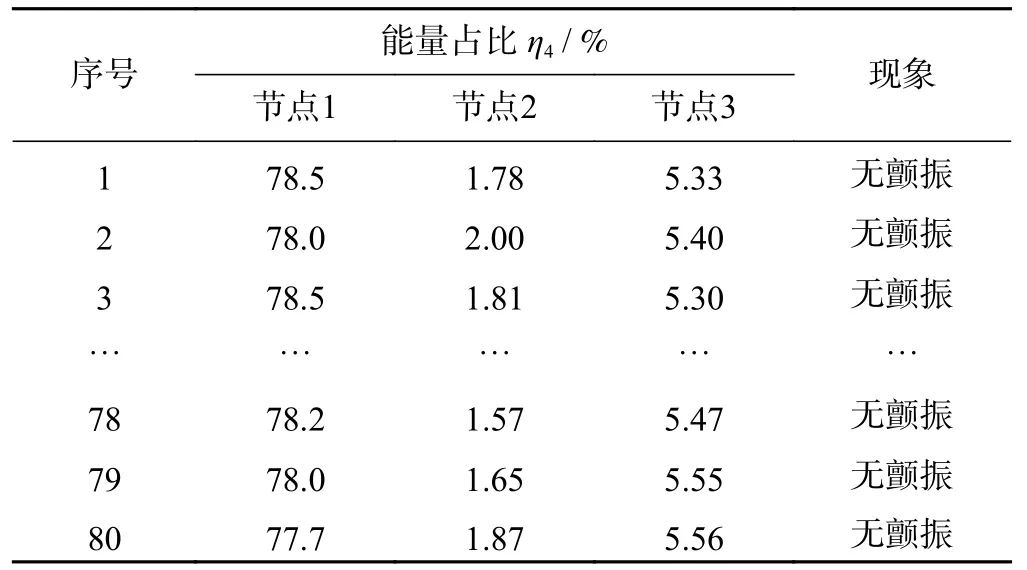
表4 高頻聲發射小波包能量占比（低速）Tab.4 High frequency acoustic emission wavelet packet energy ratio (high speed)

表5 三向振動信號特征值提取Tab.5 Eigenvalue extraction of three-way vibration signal

5 網絡訓練及識別結果

通過BP 神經網絡[13-14]算法將表5的160 組信號特征值樣本隨機排列后分為150 組訓練樣本和10 組預測樣本。模型輸入為6 個特征向量，輸出為1 個結果向量，如圖13所示。BP 神經網絡訓練時，訓練次數設為1 000 次，誤差精度為 10-3，結果中的R2越接近于1，模型效果越好[9-10]。訓練和識別過程以及10 組預測樣本得到的外圓磨削顫振真實值和預測值對比結果如圖14所示：BP 神經網絡訓練過程中的R2值大小約為0.99，說明BP 神經網絡模型訓練過程較好。從圖15中的BP 神經網絡顫振識別結果看出，真實值和預測樣本的顫振預測結果均一致。

圖13 BP 神經網絡訓練模型Fig.13 BP neural network training model

圖14 BP 神經網絡訓練過程Fig.14 BP neural network training process

圖15 BP 神經網絡顫振識別結果圖Fig.15 BP neural network chatter recognition result graph

表6為磨削顫振試驗值與預測結果對比表。從表6可以看出：BP 神經網絡模型可以對外圓磨削顫振現象有效的在線監測和識別，同時算法平均誤差在0.49%，預測結果均正確。

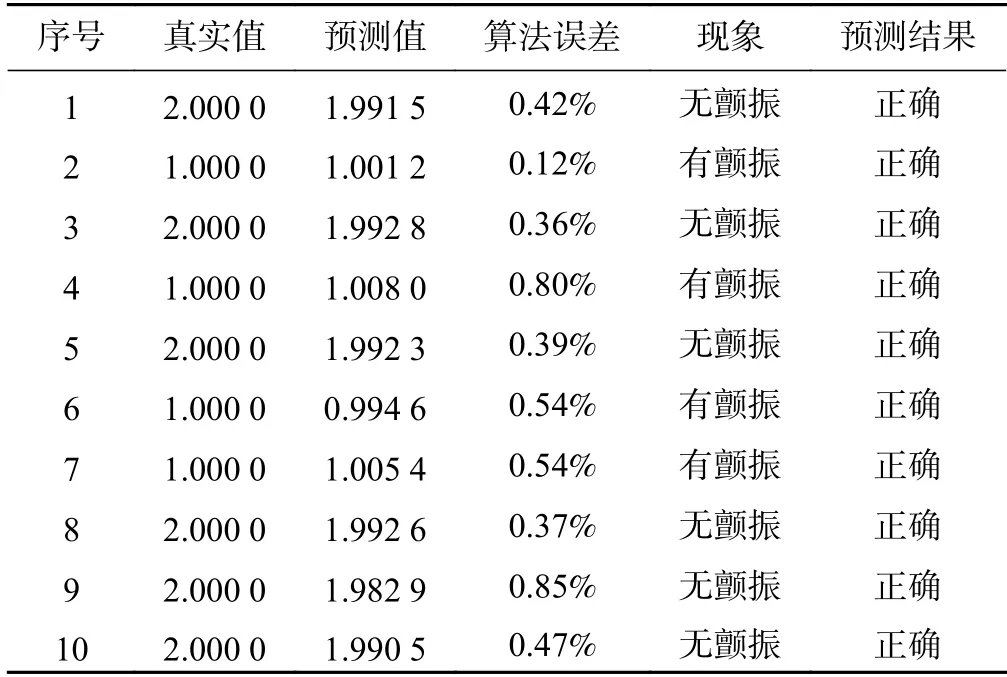
表6 預測結果數據Tab.6 Forecast result data

6 結論

針對外圓磨削顫振現象，使得工件加工表面質量降低，提出基于多特征參數樣本和BP 神經網絡的外圓磨削顫振智能監測及識別方法，并通過試驗進行算法驗證，得到如下結論：

（1）時域特征參數結合小波包分解建立的多特征參數樣本庫能有效表征機床正常磨削和磨削顫振信息，同時也能保證BP 神經網絡監測模型分類精度。

（2）利用多特征參數樣本庫對BP 神經網絡訓練學習，通過試驗驗證，BP 神經網絡算法模型能有效識別外圓磨削顫振現象，算法平均誤差0.49%。