超薄切割片的加工變形研究現狀

鄒 芹，張呈祥，李艷國，黎克楠

（1.燕山大學 機械工程學院，河北 秦皇島 066004）

（2.燕山大學 亞穩材料制備技術與科學國家重點實驗室，河北 秦皇島 066004）

（3.鄭州磨料磨具磨削研究所有限公司，鄭州 450001）

超薄切割片切割是超精密磨削的一種加工方式，在技術上屬于緩進給磨削或高效深磨[1]，有著廣泛的應用需求[2]。超薄切割片常用于電子和光學器件的精密切割[1,3]，如半導體硅晶圓劃片[4]等。加工后的工件具有低表面粗糙度、高形狀精度和高表面完整性[5]等優點。超薄切割片的厚度范圍為0.015～2.000 mm，常在0.300 mm 以下，外緣直徑范圍為50.0～152.4 mm[1,6]。其叫法并不統一。侯長紅[3]將其稱為超薄超硬材料切割砂輪；馬巖等[6]稱其為砂輪刀片；黎克楠[7]稱其為超薄砂輪。考慮到其功用，在此統一稱為“超薄切割片”。

電子和光學器件的加工對精度要求很高，用超薄切割片加工時，其自身發生的變形勢必會影響器件的加工精度。同時，磨削用量（切割片轉速、磨削深度、進給速度）也會影響器件加工后的表面質量[8-9]，需要對加工參數進行合理組合。超薄切割片在高速旋轉工作時，由于離心力和磨削力的作用易發生徑向變形，離心力使其產生徑向擴張，而磨削力導致其徑向壓縮。離心力和磨削力均與磨削用量有關。超薄切割片在不同磨削用量下發生不同的徑向變形，這種徑向變形會使實際磨削深度發生變化，影響工件的加工精度[10]。明確磨削用量對切割片變形量的影響有助于優化及選擇加工參數，且加工時補償切割片變形量有助于提升加工精度[7]。

基于上述情況，綜述磨削用量對超薄切割片變形影響的研究現狀。內容主要涉及彈性變形和塑性變形的理論研究、有限元模擬結果和相關試驗研究。

1 超薄切割片變形理論研究

圖1顯示了一些常見型號的超薄切割片[7]，其橫截面輪廓各不相同。超薄切割片為彈性體，工作時易發生徑向變形，變形類型有彈性變形、塑性變形。

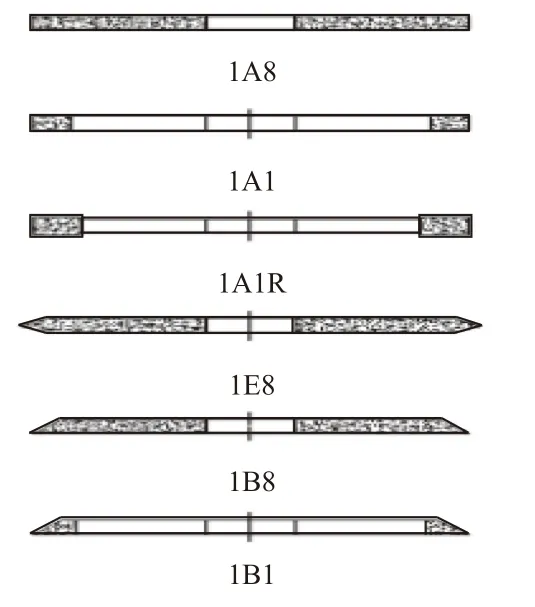
圖1 常見的超薄切割片型號Fig.1 Common ultra-thin dicing blade models

1.1 超薄切割片彈性變形

超薄切割片作為一種圓環狀薄板結構工具，其徑向尺寸遠大于軸向尺寸，因而可視作平面應力問題。當繞回轉軸以固定的角速度ω旋轉時，超薄切割片在極坐標系下承受的徑向體力為離心力ρω2r，環向體力為0。其中，ρ是超薄切割片的密度，r為半徑。此時，作為軸對稱的物體受軸對稱的體力，超薄切割片的應力也呈軸對稱分布[11]，即切應力為0，徑向正應力和環向正應力均為主應力[12]，環向平衡微分方程自然滿足，幾何方程得到簡化。

超薄切割片彈性變形時的理論公式推導步驟為：（1）建立切割片的受力模型，通常使用極坐標系，圖2為超薄切割片承受離心力時的受力模型[13]，微小單元ABCD在徑向受到徑向體力F和徑向正應力（AB面上的σr和CD面上的），在環向受到環向正應力（BC面上的σθ和DA面上的σθ）；（2）聯立平衡微分方程、幾何方程、應變相容方程（變形協調方程）和物理方程，得到只含一個未知量的微分方程。另一種處理方式為，引入與應力分量相關的一個應力函數，將以應力分量為變量的徑向平衡微分方程和以應力分量為變量的相容方程聯立，簡化為只含應力函數的一個未知量的微分方程[11]；（3）求解微分方程，得到含2 個相同待定系數的徑向正應力、環向正應力和徑向位移通解表達式；（4）代入邊界條件確定待定系數，得出徑向正應力σr、環向正應力σθ和徑向位移ur的表達式。

圖2 離心力下超薄切割片的受力模型Fig.2 Force model of ultra-thin dicing blade under centrifugal force

等厚度超薄切割片高速空轉時在其表面所受面力為0，邊界條件為內徑處自由和外徑處自由，即σr|r=a=0 和σr|r=b=0[14]，推導得到其徑向正應力表達式式（1）、環向正應力表達式式（2）、徑向位移表達式式（3）[12]。這里不考慮切割片的剛體位移，認為其環向位移為0[11]。有些學者使用歸一化量和無量綱量來表達這些公式，含義是一樣的。

式中：ν為超薄切割片的泊松比，ω為超薄切割片的角速度，E為超薄切割片的彈性模量，a為超薄切割片的內孔半徑，b為超薄切割片的外圓半徑。

相比HU[12]推導的公式，馬巖等[6]推導的徑向正應力公式和環向正應力公式的第一項為若含有重力加速度g項，式（1）和式（2）等號左端應力的量綱為ML-1T-2，而公式等號右端總量綱由ML-1T-2變為ML-1。其中，ν的量綱為1；ρ的量綱為ML-3；ω的量綱為T-1；a、b、r的量綱均為L；g的量綱為LT-2。等號左右兩端量綱不相等，等式不成立。因此，g不應該存在。

張磊等[13]推導的環向正應力公式括號內的第3 項為，而其他學者得到的結果是該項的符號為正號[12,14]。對此，筆者重復該公式的推導過程，得到的結果符號為正號。并且，張磊等[13]的圖中數據經過計算驗證，符合正號時得出的結果而不符合負號時得出的結果。張磊等在該公式的書寫應該是出現了筆誤。因此，該項應為 +

由式（1）和式（2）可得到整個圓盤的應力分布，根據式（3）可得圓盤任意位置的變形情況。上述公式表明[12]，徑向正應力、環向正應力和徑向位移均為不同角速度下半徑的函數。超薄切割片上相同半徑處的點具有相同的應力和徑向位移。因結構相似，上述公式也適用于砂輪和圓鋸片，其中，超薄切割片的研究可以參考砂輪和圓鋸片應用這些公式得出的結論。

馬巖等[6]應用上述理論公式計算所得數據繪制的應力分布圖直觀顯示：環向正應力始終大于徑向正應力，兩者均為拉應力。由于徑向正應力和環向正應力均為主應力，因此，環向正應力為第一主應力，徑向正應力為第二主應力。應力分布上，環向正應力在內徑處最大，沿徑向向外逐漸減小，徑向正應力沿徑向由0 先增大而后減為0，在半徑為處存在最大值[12]，σrmax=因此，MA[15]認為環向正應力是超薄切割片高速旋轉破壞的主要因素，將拉伸強度代入環向正應力公式可得到超薄切割片發生破壞的極限角速度。

關于徑向位移，趙忠虎等[16]根據最大值原理對徑向位移公式求導，得到了圓盤勻速轉動時徑向位移的最大值點與位移最大值。發現位移的最大值點在圓盤內部，把外徑處的位移值作為最大值是不合適的。張磊等[13]發現孔徑比會影響徑向位移變化趨勢，相同外緣線速度不同孔徑比下徑向位移最大值的位置并不恒定，并隨內外徑尺寸的變化有極小點。

LI 等[14]在研究1A8 型金屬結合劑金剛石超薄切割片時，考慮到超薄切割片是一種含孔隙多材質的混合物，根據組成復合材料理論，使用混合等效密度ρc、混合等效彈性模量Ec和混合等效泊松比νc，得到更符合實際的σr、σθ、ur的表達式。

其中：ρc=ρm(1-Vd-Va)+ρdVd+ρaVa，ρm為金屬結合劑密度，ρd為金剛石密度，Vd為金剛石體積分數，ρa為氣孔的密度，Va為氣孔的體積分數；Ec=EmVmEdVd(1-1.9Va+0.9Va2)，Vm為金屬結合劑的體積分數，Em為金屬結合劑的彈性模量，Ed為金剛石的彈性模量；vc=vmVmνdVd(1-1.9Va+0.9Va2)，νm為金屬結合劑的泊松比，νd為金剛石的泊松比。

由于實際影響加工的是外徑處的徑向位移，因此其數值必須明確。將角速度轉化為轉速，代入ω=2πn/60得切割片外徑處的彈性變形公式式（7）[14]。可以看出，超薄切割片的徑向擴張變形量與轉速的二次方呈線性關系，隨轉速升高而增大。低密度和高彈性模量的材料有利于減少徑向擴張變形。因此，基體式超薄切割片可以在基體材料上優化設計，如使用TiAl 合金及其復合材料[17]。高熵合金也因其優異的力學性能[18]，被嘗試用作超薄切割片的結合劑[7]。

LI 等[14]認為超薄切割片在高速工作時相較于靜態時其徑向尺寸存在變化，提出動態直徑Dd的概念。動態直徑為靜態直徑Ds加上外緣變形量，即：Dd=Ds+2(ur)r=b，推導出超薄切割片在高速運轉發生彈性變形時的動態直徑公式式（8）。

超薄切割片在不同轉速下的動態直徑如圖3所示[14]，理論計算值與試驗測量值具有較好的一致性。

圖3 不同轉速下的動態直徑[14]Fig.3 Dynamic diameter at different speeds[14]

在其他參數保持不變時，超薄切割片的直徑隨轉速升高而增大，如φ58 mm 銅基結合劑超薄切割片在50 000 r/min（線速度為151.77 m/s）時動態直徑增幅為0.116 mm。此時，其動態直徑為58.116 mm，為靜態直徑（58 mm）的1.002 倍[14]。常見的應用如光纖分路器石英V 槽的加工深度僅為0.15 mm，超薄切割片的變形不容忽略。因此，使用超薄切割片時考慮其徑向變形并將其應用于加工時的補償，對加工精度的提高是有益的。在應用超薄切割片進行超高速精密磨削時可以實現微米級的進給量[19]，可以將徑向變形量補償到磨削深度上，但目前缺乏相關的補償研究。

有些學者在研究變厚度切割片時將其整體看作平面問題，應用上述公式預測變形。這種簡化必將帶來誤差。LI 等[14]應用上述等厚度情況的理論公式來預測1E8 型切割片的徑向變形量，理論預測變形量與試驗測量值存在較大差異。試驗結果還顯示：相同尺寸和材料的1A8 和1E8 型切割片在相同轉速下的徑向變形量是不同的。

關于變厚度圓環盤，EKHTERAEITOUSSI 等[20]將整個圓環盤離散成無數個微圓環來研究彈性變形。認為每個微圓環都是等厚度的，微圓環的邊界條件為σr|r=r1=σ1和σr|r=r2=σ2，得到微圓環的徑向正應力表達式式（9）、環向正應力表達式式（10）和徑向位移表達式式（11）。

F1和F2分別為微圓環內、外圓柱面上單位長度的力，δ為厚度，即F1=σ1δ1、F2=σ2δ2。根據相鄰微圓環間的位移和力的連續性可以求出整個圓環盤任意位置的應力值和徑向位移量[20]。

學者們也研究了不同材料屬性的薄圓盤，以減少圓盤的徑向變形和改善應力分布情況。由功能梯度材料（functionally graded materials,FGM）制成的圓盤一直被廣泛研究[21]。這種圓盤從內徑到外徑由一種材料逐漸過渡成另一種材料，材料間結合良好，彈性模量、拉伸屈服應力和密度均為半徑的函數。研究集中在不同邊界條件、材料、截面輪廓下旋轉圓環盤的應力分布、應變分布和徑向變形情況[21-23]，這些研究的邊界問題均是軸對稱的。邊界條件為內徑處自由和外徑處自由時，等厚度的功能梯度材料圓環盤相比單種均質材料圓環盤，具有相同的徑向位移變化趨勢，但變形量更大，且隨冪定律梯度指數的增加而增加[22]。THAWAIT 等[24]研究了邊界條件為內徑處夾緊和外徑處自由的變厚度功能梯度材料圓盤，發現彈性模量和密度均更大的材料放置在外緣的圓盤變形量更小。因此，若使用功能梯度材料制造切割片可以采用這種材料排布方式。

圓盤也常使用正交各向異性材料，徑向與環向的彈性模量不同。CALLIOGLU 等[25]研究了曲線變厚度正交各向異性材料環形盤的彈塑性應力，確定了其應力分布情況。對于各向異性功能梯度夾層圓環盤，彭旭龍等[26]分析了材料的非均勻特性和各向異性對應力和位移分布的影響。研究結果表明：增大梯度參數可改善結構內徑向應力以及徑向位移分布。

常用的超薄切割片為各向同性的均勻連續材料，邊界條件為內孔自由和外圓自由。上述研究對超薄切割片的結構和材料設計具有指導意義。

1.2 超薄切割片塑性變形

上述研究得出的切割片變形的理論公式均是基于彈性力學理論。只發生彈性變形時，由上述公式得出的變形量與試驗測量值一致性好。當轉速增加以至于發生塑性變形后，兩者會存在較大偏差[14]。

當轉速不斷升高，存在臨界轉速，超過臨界轉速時，超薄切割片發生塑性變形[12]。對于圓環形切割片，塑性變形最先發生在內孔處，因為該處的應力分量最先滿足屈服準則[23]。當轉速高于臨界轉速時，切割片處于部分屈服狀態，存在彈/塑性變形邊界。圖4[23]顯示出切割片的變形情況，以半徑為c的圓柱面為邊界，呈2 個環狀區域，內環為塑性變形區，外環為彈性變形區。隨著轉速繼續升高，塑性變形區域逐漸延伸至外徑，整個切割片處于完全塑性變形狀態[20]。

圖4 彈/塑性變形區域示意圖Fig.4 Schematic diagram of elastic/plastic deformation area

研究超薄切割片的變形需要明確其變形類型和變形量。可通過應力分析來確定變形類型是彈性變形還是塑性變形。而在實際加工中，超薄切割片的變形類型經常被忽略，這是不合理的。因為發生塑性變形是不可逆的，將會影響加工精度。

KAMAL 等[27]研究了圓環盤與心軸過盈裝配時的旋轉變形情況，應用特雷斯卡屈服準則（Tresca yield criterion）及其相關流動法則，得出了塑性區的環向正應力、徑向正應力和徑向位移的理論公式。在彈性區進行上述彈性力學的理論推導時，邊界條件有所不同。在彈/塑性變形邊界處，開始滿足屈服準則，并且塑性位移與彈性位移相等，徑向應力也同樣相等。根據該邊界處位移和應力連續可以確定邊界半徑c，運用c等于內徑a得到開始塑性變形時的臨界角速度；運用c等于外徑b得到完全塑性變形時的臨界角速度。與應用米澤斯屈服準則（Mises yield criterion）及其相關流動法則分析塑性區相比，得到的結果差距很小。旋轉的超薄切割片也可以采用相似的推導過程來得出彈/塑性變形區的正應力和徑向位移的理論公式，不過內徑處的邊界條件為徑向正應力等于0。

邊界條件為內徑處自由和外徑處自由的等厚度圓環盤在發生塑性變形時，隨著塑性變形區域擴展至整個圓環盤，環向正應力在徑向逐漸接近等值分布[28]。EKHTERAEITOUSSI 等[20]應用米澤斯屈服準則研究該盤在完全塑性變形時的狀態，得到了圓環盤開始完全塑性變形時的角速度，并且圓盤厚度不影響該值。理想彈塑性材料制成的圓環盤旋轉時超過該角速度會發生無限制的塑性流動，此時是不穩定狀態，將該角速度稱為極限角速度[12]。當采用一種應變強化材料（Ramberg-Osgood 材料）時，超過該角速度不一定會導致無限的變形。研究表明：截面輪廓也會影響圓盤的變形，錐形截面輪廓的圓盤相比凸形或凹形輪廓具有更高的極限速度。由此可知，超薄切割片可以在截面輪廓上優化設計，采用錐形輪廓以實現更高速的加工。上述研究中的截面輪廓或者說厚度函數均是關于半徑且范圍為內徑到外徑的連續函數，但如1E8 型超薄切割片這種厚度函數為分段函數的情況缺乏相應研究。

磨削深度是決定工件表面形態的主要因素，磨削力對硬脆材料的磨削有重大影響[29]。董世明等[30]分析了超薄切割片這類平面應力圓盤在外圓周面分別承受徑向集中載荷和局部徑向分布載荷時的應力場和位移場。結果表明：外圓周面的徑向位移在載荷作用區域外急劇減小，并且，載荷作用區域內的徑向位移在徑向分布上隨著遠離載荷作用點而逐漸減小。即超薄切割片在受法向磨削力時主要在載荷作用區域發生局部變形。王啟智[31]把巴西圓盤實驗從平臺巴西圓盤推廣到中心圓孔平臺巴西圓盤，可以用于切割片在受磨削力時的分析。

轉速引起離心力，使得超薄切割片變形表現為徑向膨脹。而磨削深度和進給速度對超薄切割片變形的影響轉化為該磨削用量下的磨削力引起超薄切割片在磨削區域的局部徑向壓縮。研究集中在磨削力模型的建立。不同的工件材料被具體分析得出了磨削力經驗公式[32-33]，有些材料還被確定出單顆磨粒的磨削力[34-35]。只考慮離心力的研究中，超薄切割片在空轉，并沒有實際加工。在加工時，通過對刀可以減小空轉變形對加工精度的影響[36]。目前，缺少磨削深度和進給速度對超薄切割片變形影響的理論研究。該理論研究的難點在于此時考慮磨削力，超薄切割片的徑向變形問題不再是軸對稱問題，受力情況更為復雜，表現在同時存在正應力和切應力，并且邊界條件不確定。如果邊界條件數量不夠則解析法無解。同時，循環載荷作用下的材料力學性能與靜態載荷時不同[37]。

上述研究結果表明，切割片轉速對超薄切割片徑向變形的影響已經推導出了完善的理論公式，可以實現很好的預測。

2 有限元模擬分析

使用有限元法的研究步驟為[38-39]：（1）在有限元分析軟件中導入或直接建立超薄切割片的模型，模型要考慮超薄切割片的材料參數和尺寸形狀參數；（2）采用合適的網格劃分方法對模型劃分網格；（3）根據超薄切割片的運動情況確定模型的約束條件并施加約束；（4）對模型施加載荷。只考慮離心力時，在內孔處設置軸向約束和環向約束，設置角速度產生離心力。考慮磨削力時，則要計算出載荷作用區域及其數值大小。磨削力大多采用試驗獲得的經驗方程。

應用有限元分析軟件通過上述過程可得出超薄切割片在受離心力、磨削力及離心力和磨削力時的應力和位移。應力分布和位移分布可以通過云圖顯示。云圖采用等值線表示應力、位移分布，使用不同的顏色區分數值大小。應力云圖可以直觀顯示超薄切割片各處的應力值，應力值較大的危險區域清晰可見；位移云圖可用于分析任意位置的變形量。

有限元模擬作為一種方便的方法被用于超薄切割片的研究。馬巖等[6]使用有限元分析軟件得到了矩形截面超薄切割片在只受離心力時的環向正應力云圖、徑向正應力云圖和等效應力云圖。應力云圖顯示的應力分布與理論上的結果具有高度的一致性。環向正應力在內徑處接近于等效應力。等效應力云圖顯示最大等效應力遠小于材料的抗拉強度。這說明超薄切割片在設定的轉速下是安全的。MA[15]應用有限元分析軟件ANSYS 得到超薄切割片在不同轉速下的等效應力云圖。等效應力云圖均表明：從內徑到外徑，等效應力逐漸減小，其中轉速為35 000 r/min 時的等效應力云圖如圖5所示。

圖5 等效應力云圖[15]Fig.5 Equivalent stress nephogram[15]

超薄切割片的研究處于起步階段，有限元模擬的數據較少，尤其是考慮磨削力的研究。與之結構相似的砂輪和圓鋸片的有限元分析研究較多，可以為超薄切割片的相應研究提供參考。

李陽[39]得到了圓鋸片在分別受離心力、磨削力、離心力和磨削力時的變形云圖。載荷作用區域的磨削力包括法向磨削力和切向磨削力。當圓鋸片只受磨削力時，載荷作用處的變形最劇烈，沿徑向至內徑處，變形量逐漸減小。磨削力引起的壓縮變形比離心力引起的膨脹變形在數值上高2 個數量級。離心力和磨削力共同作用下圓鋸片的最大變形位于工作齒處，為徑向壓縮變形。張進生等[40]研究了一種組合結構金剛石圓鋸片的變形情況，發現其承受離心力和磨削力時與只受離心力時相比，在磨削力作用的圓鋸片外徑處，磨削力抵消了10%由離心力引起的徑向膨脹變形量。應用于高速/超高速磨削的超薄切割片承受更大的離心力，隨著線速度的升高，磨削力會進一步降低[8]，具體變形情況則缺少研究。法向磨削力與離心力方向相反，導致的徑向變形量和變形類型需要具體分析。同時，材料也影響變形。SONDHI 等[41]將理論公式導入ANSYS的UDF 子程序，研究了內徑處自由和外徑處自由的邊界條件下梯度參數和正交各向異性程度對功能梯度變厚度正交異性圓盤的位移的影響。KIZAKI 等[42]借助有限元分析軟件ABAQUS 設計出一種內環使用鋼、外環使用纖維沿環向排布的碳纖維增強塑料、最外圓為磨料層的砂輪。有限元模擬表明：在空轉相同轉速時，相比同尺寸下完全使用鋼的砂輪，其徑向膨脹變形減少了59%，最大主應力也有很大程度的減小。這種結構的砂輪在加工剛性平板工件時易發生更大的擠壓變形，不過擠壓變形量（幾微米）相比旋轉膨脹變形量（幾十微米）較小。

磨削時磨具的變形是熱力耦合問題。代東波[43]在研究CBN 砂輪由離心力引起的變形時，同時考慮磨削力轉化成熱量引起的熱變形。結果表明，隨著線速度的增大，總徑向變形呈先下降后上升的趨勢。在線速度增大的前段，隨著磨削深度的增加，砂輪在磨削區域處的熱變形量與總徑向變形量均增大。但在后段高線速度下，中間值的磨削深度參數時卻引起最大的總徑向變形量，具體原因并不明確。

上述研究結果表明：不同的磨削用量組合產生不同大小的離心力和磨削力，離心力和磨削力引起的徑向變形存在抵消現象，變形情況應具體分析。承受磨削力以及磨削力和離心力共同作用下的超薄切割片變形情況有待研究。有限元模擬可以作為一種有效的方法，用于開展相應的研究。

3 試驗研究

試驗可以表明超薄切割片的真實變形情況，常用來對比以確定研究結果的可靠性。理論研究和有限元模擬這2 種研究方式獲得的變形量相比試驗測量值均在工程應用可接受的程度，驗證了結果的可用性。

關于超薄切割片外徑處變形量的測量方式，只考慮離心力時，LI 等[14]采用一種非接觸式紅外測量方式，如圖6所示。將超薄切割片放置在紅外光學位移傳感器的發射端和接收端之間，測量值為相對靜態直徑的增量，進而得到超薄切割片在不同轉速下的動態直徑。激光位移傳感器也可以作為一種非接觸測量方式用來測量徑向位置變化[36]。測得超薄切割片轉動時的徑向變形量后，停轉超薄切割片，再次測量，確定其在該轉速下是否發生塑性變形以及塑性變形量。考慮磨削力時，超薄切割片切入工件內部，磨削區域處的變形量在線測量困難。高東恩[44]將砂輪按照相同的磨削深度切入精磨外圓的圓柱形工件，使用激光位移傳感器測量不同線速度下磨削后的梯形槽，得到了不同砂輪線速度下的徑向變形量。YAMADA 等[45]使用輪廓測量裝置測量了普通磨削磨槽的實際磨削深度。結果表明：實際磨削深度小于設定的磨削深度，并隨進給速度增大而減小。這些測量方式是可行的。超薄切割片切割磨削時的變形情況有待實際測量。

圖6 動態直徑測量示意圖Fig.6 Schematic diagram of dynamic diameter measurement

在彈性階段的徑向變形量研究中，理論預測值相比試驗測量值常存在一些偏差，原因主要是：（1）理論公式推導時進行了多種簡化和假設；（2）超薄切割片在不同線速度下的彈性模量和泊松比不恒定[7]，而在理論公式中將其認為是恒定值；（3）試驗時存在測量誤差也會造成影響。

研究磨削力引起的徑向變形需要首先知道磨削力的大小。試驗測得的磨削力可以用于超薄切割片切割磨削時變形的理論公式推導和有限元模擬時載荷的施加。JIANG 等[46]對超薄切割片高速鋸切石英玻璃的磨削力進行了試驗研究。測量結果顯示：法向磨削力和切向磨削力均很小，不到1 N；在固定材料去除率下，提高切割片轉速有助于降低磨削力。低磨削深度和低進給速度也帶來磨削力的降低。在其研究中，使用測力儀測量磨削力，測得的各軸磨削力分別近似看作法向磨削力與切向磨削力。不過，磨削時超薄切割片與工件為弧形接觸，這種近似難免存在偏差。SHEN 等[47]在緩進給切割磨削時基于磨削力與切屑厚度成正比的假設，認為接觸弧區域的應力為梯形分布，并將測得的各軸磨削力經過力的矢量計算得到法向磨削力和切向磨削力。這樣處理的結果更為準確。

總的來說，超薄切割片的相關試驗較為缺乏。空轉時的徑向變形量容易測量；切入工件時，可行的徑向變形量測量方式需要被提出。通過試驗可以不斷調整磨削用量，以減少超薄切割片的徑向變形。同時，可以開展補償試驗，在磨削深度上對變形量進行補償，確定合適的補償量以提高加工精度。

4 結論與展望

在超薄切割片的加工變形研究中，理論研究、試驗和有限元模擬3 種研究方式分別有各自的優點。其中，試驗最貼合實際，但任一項加工參數的變化都需重新操作，費時煩瑣；使用理論公式和通過有限元模擬均可快速得到超薄切割片在任意加工參數下的變形量，且與試驗結果誤差在可接受范圍，具有可行性。超薄切割片加工變形的相關理論研究仍需不斷推進，以推導出更貼合實際的理論公式。相關的試驗數據建議進行總結，建成數據庫，以便于查閱。有限元模擬的研究數據較少，作為一種有效的研究方式，建議擴大其應用范圍。

切割片轉速對其徑向變形影響的研究相對深入，已形成一個較為完整的體系。而磨削深度和進給速度的研究只停留在少量試驗數據和有限元模擬分析階段，應推進相關研究。超薄切割片工作時在槽內測量困難，變形量測量方法的缺失限制了相關研究結果的驗證，可行的測量方法需要被提出。