幾類帶空轉移的n元偽加權自動機的關系*

趙路瑤,王海輝,李 平

(陜西師范大學數學與信息科學學院,陜西 西安 710119)

1 引言

自動機理論是計算機科學理論的基礎。1961年,Schützenberger[1]提出了加權有窮自動機的概念。加權有窮自動機是經典的非確定型有窮自動機的狀態(tài)轉移函數、初始狀態(tài)和接受狀態(tài)都附加上權重而形成的一種有窮自動機,這些權值形成的代數結構一般為半環(huán),得到了廣泛研究[2 - 6]。1967年,Wee[7]提出了模糊有窮自動機的概念,開啟了模糊自動機理論研究的歷程。此后,又有學者相繼提出了取值于完備正交模格的自動機[8，9]、取值于完備剩余格的有窮自動機[10,11]和取值于格序半群的模糊有窮自動機[12]。作為以上各種模型的擴展,2010年,Droste等[13]提出了取值于強雙半群(偽半環(huán))的自動機理論,且進行了深入研究[14,15]。偽半環(huán)是半環(huán)去掉分配律形成的代數結構,因此偽加權有窮自動機(取值于偽半環(huán)的加權有窮自動機)比取值于半環(huán)的加權有窮自動機更具一般性。

近一個世紀以來,自動機理論取得了長足發(fā)展,其廣泛地應用于人工智能、文本處理、數字圖像壓縮、模型檢測和模式識別等領域[16 - 21]。近來,我們發(fā)現(xiàn)自動機也可以應用于不確定性數據處理中,以解決不確定性數據世系分析中結果元組的概率計算問題[22,23]。然而解決此問題需要一個可以帶有有限多個輸入的自動機,以往的自動機概念都只帶有一個輸入或帶有輸入與輸出2個信息,因此本文提出n元偽加權有窮自動機(帶有n個有限輸入字符集的偽加權有窮自動機)、分明型n元偽加權有窮自動機(初始狀態(tài)與狀態(tài)轉移函數均是分明的n元偽加權有窮自動機)與確定型n元偽加權有窮自動機(初始狀態(tài)與狀態(tài)轉移函數均是確定的n元偽加權有窮自動機)的概念。

在經典的有窮自動機理論中,帶空轉移的非確定型有窮自動機、非確定型有窮自動機與確定型有窮自動機是等價的[24,25]。在基于格序半群的模糊自動機理論中,除初始狀態(tài)與接受狀態(tài)均是分明的非確定型格值自動機以外,其他類型的非確定型格值自動機與帶空轉移的非確定型格值自動機均是等價的[26],而非確定型格值自動機與確定型格值自動機并不是等價的[12]。由格序半群和半環(huán)的代數性質可知,這些結論推廣到取值于半環(huán)上的加權自動機依然成立。此外,在已知確定型加權自動機與非確定型加權自動機并不等價的前提下,文獻[27]提出了狀態(tài)轉移函數是分明的加權自動機、帶空轉移的狀態(tài)轉移函數是分明的加權自動機的概念,并證明了以上二者是等價的,且它們與確定型加權自動機也是等價的。

然而由于偽半環(huán)未必滿足分配律,以上結論并不能直接推廣到偽加權有窮自動機中,并且到目前為止還沒有文獻直接討論偽加權有窮自動機與帶空轉移的偽加權有窮自動機之間的等價性關系。因此,本文以n元偽加權有窮自動機為基礎,根據狀態(tài)轉移函數在每個字符集上是否帶空轉移,將n元偽加權有窮自動機與分明型n元偽加權有窮自動機分為4類:帶r-型空轉移的n元偽加權有窮自動機、帶空轉移的n元偽加權有窮自動機、帶r-型空轉移的分明型n元偽加權有窮自動機和帶空轉移的分明型n元偽加權有窮自動機,并研究了上述幾種類型的自動機之間的關系,討論了狀態(tài)轉移函數在每個字符集上是否帶空轉移對其接受語言的影響,進一步完善了偽加權有窮自動機理論。

2 預備知識

首先回顧一下偽半環(huán)的概念及其相關結論。

注1在文獻[15]中,偽半環(huán)又叫做強雙半群。

例1[15]易驗證下面的代數結構都是偽半環(huán):

(1)(N,+,×,0,1)、(R,+,×,0,1)與([0,1],max,×,0,1)都是偽半環(huán)。其中,(N,+,×,0,1),(R,+,×,0,1)是交換且分配的,([0,1],max,×,0,1)是交換且加冪等的。

(2)格序半群是偽半環(huán)。同時,它們也是加冪等且分配的。

(3)格、完備格、完備正交模格和完備分配格都是偽半環(huán)。其中,格、完備格、完備正交模格、完備分配格均是交換、加冪等且乘冪等的。此外,完備分配格還是分配的。

3 n元偽加權有窮自動機及其識別的語言

本節(jié)給出n元偽加權有窮自動機、分明型n元偽加權有窮自動機和確定型n元偽加權有窮自動機的概念,并分別給出它們所識別的語言的定義。下面先回顧一下偽加權有窮自動機的定義。

定義2[15]偽加權有窮自動機PA(Pseudo weighted Automata)是一個五元組A=(Q,Σ,δ,I,F),其中,

(1)Q為有限狀態(tài)集,Σ為有限輸入字符集;

令Σ*表示Σ關于連接運算生成的自由幺半群,ε是其單位元。對任意θ∈Σ*,|θ|表示θ的長度,即字符的個數,特別地,|ε|=0。

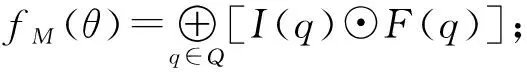
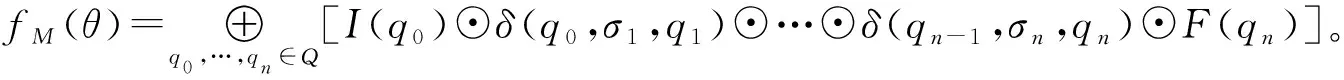
定義4n元偽加權有窮自動機(n-PA)是一個n+4元組M=(Q,Σ1,…,Σn,δ,I,F),其中,

(1)Q,I,F的意義同定義1;

(2)Σi為有限字符集,i=1,…,n;

若存在i,j,使得|θi|≠|θj|,則fM(θ1,…,θn) =0;

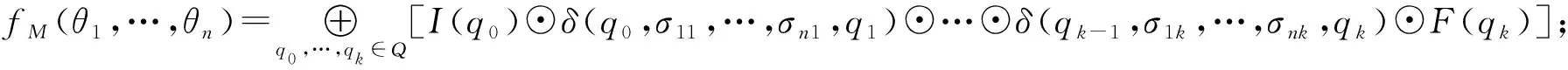
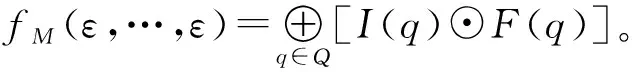
顯然,當n=1時,n元偽加權有窮自動機即為偽加權有窮自動機。

定義5設M=(Q,Σ1,…,Σn,δ,I,F)是一個n-PA,若I={q0},δ:Q×Σ1×…×Σn→2Q,則稱M為分明型n元偽加權有窮自動機n-CPA(n-ary Crisp Pseudo weighted Automata)。

若|θ1|=…=|θn|=0,即θ1=…=θn=ε,則δ*(q,θ1,…,θn)={q};

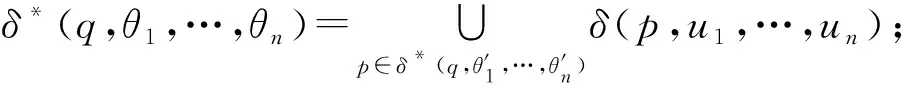
否則,δ*(q,θ1,…,θn)無定義。

定義6設M=(Q,Σ1,…,Σn,δ,I,F)是一個n-PA,若I={q0},δ:Q×Σ1×…×Σn→Q,則稱M是一個確定型n元偽加權有窮自動機n-DPA(n-ary Deterministic PA)。

若|θ1|=…=|θn|=0,即θ1=…=θn=ε,則δ*(q,θ1,…,θn)=q;

若|θ1|=…=|θn|>0,不妨設θ1=θ′1u1,…,θn=θ′nun,則δ*(q,θ1,…,θn) =δ(δ*(q,θ′1,…,θ′n),u1,…,un);

否則,δ*(q,θ1,…,θn)無定義。

fM(θ1,…,θn)=

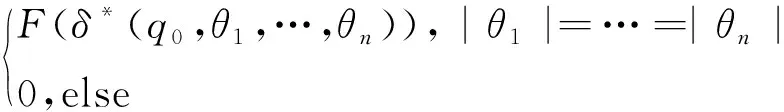
為方便起見,若I={q0},那么記M=(Q,Σ1,…,Σn,δ,q0,F)。

注3設Σ1,…,Σn是非空有限字符集,則由文獻[27]中的定理4.1與文獻[12]中的定理3.3可推出L(n-DPA,Σ1,…,Σn)=L(n-CPA,Σ1,…,Σn)L(n-PA,Σ1,…,Σn)。即n-DPAs與n-CPAs是等價的,但與n-PAs并不是等價的。稱2個自動機是等價的是指它們所接受的語言類型是相同的。

4 帶r-型空轉移的n元偽加權有窮自動機及其識別的語言

本節(jié)將根據狀態(tài)轉移函數在每個字符集上是否帶空轉移,將n元偽加權有窮自動機進一步分類,給出它們分別接受語言的定義并討論它們之間的關系。

定義7帶r-型空轉移的n元偽加權有窮自動機(n-rEPA)是一個n+4元組：

其中,

(1)Q,I,F的意義同定義2;

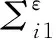
為給出M接受語言的定義,給出以下符號和概念。

又令PM=EM∪{π|π=e1e2…em(m≥2),ei∈EM,i=1,…,m,且π滿足n(ei)=c(ei+1),i=1,…,m-1}。那么對任意π∈PM,稱π是M的一條路徑。例如,π1=(q1,ε,σ2,…,σn,q2)與π2=(q0,ε,σ2,…,σn,q1)(q1,σ1,…,σn-1,ε,q2)是M的2條路徑,而π3=(q0,ε,σ2,…,σn,q1)(q2,σ1,…,σn-1,ε,q3)并不是M的路徑。

當θ1,…,θn不全為ε時,

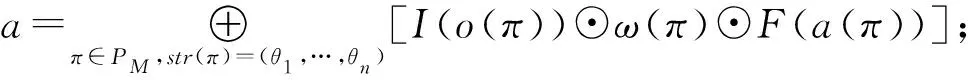
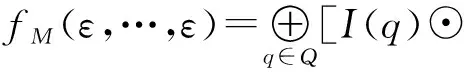
此外,注意到,對于一個n-PAN=(Q,Σ1,…,Σn,δ,I,F),其接受的語言具有等價形式:

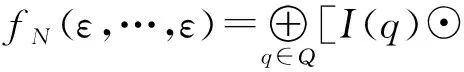
當θ1,…,θn不全為ε時,

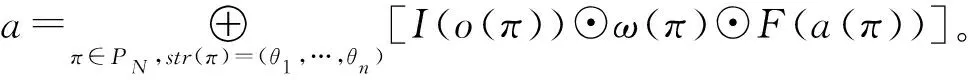
由此可見,n-PA是一個特殊的n-rEPA。

定義8帶空轉移的n元偽加權有窮自動機(n-EPA)是一個n+4元組:

其中,

(1)Q,I,F的意義同定義1;

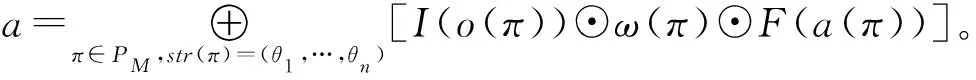
定理1設Σ1,…,Σn是非空有限字符集,則L(n-PA,Σ1×…×Σn)L(n-rEPA,Σ1×…××…××…×Σn),其中,{i1,…,ir}是{1,…,n}的任意一個子序列。

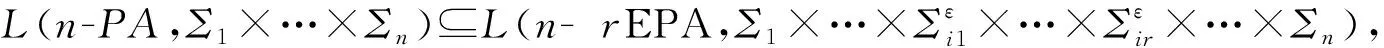
δ1(q,u1,…,un,p)=

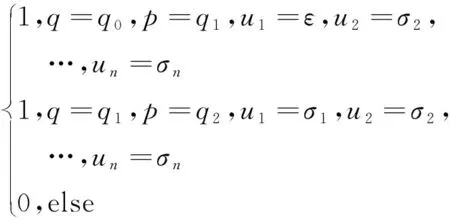
構造過程如圖1所示。

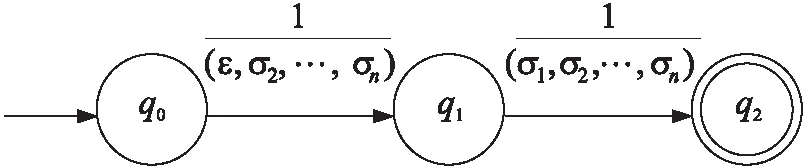
Figure 1 n-rEPA M圖1 n-rEPA M

□

□

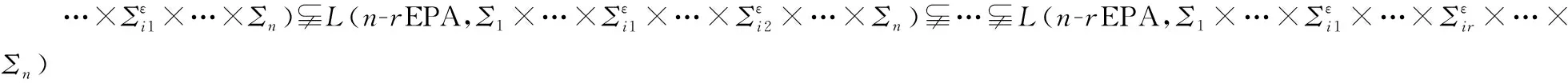
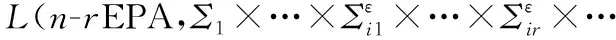
由定理1和定理2可得以下推論。

推論1設Σ1,…,Σn是非空有限字符集,則L(n-PA,Σ1×…×Σn)L(n-rEPA,其中,{i1,…,ir}是{1,…,n}的任意一個真子序列。

由以上定理與推論可知,n-PAs、n-rEPAs與n-EPAs三者均不是等價的。

下面介紹帶r-型空轉移的分明型n元偽加權有窮自動機的定義。

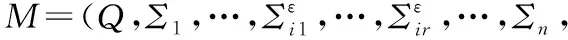
類似于定義7,首先給出以下概念。

又令PM=EM∪{π|π=e1e2…em(m≥2),ei∈EM,i=1,…,m,且π滿足c(ei+1)∈δ(ei),i=1,…,m-1}。那么對任意π∈PM,稱π是M的一條路徑。例如,若δ(q1,σ1,…,σn)={q2},δ(q2,σ1,…,σn)={q3},則π1=(q1,σ1,…,σn)與π2=(q1,σ1,…,σn)(q2,σ1,…,σn)是M的2條路徑,而π3=(q2,σ1,…,σn)(q1,σ1,…,σn)并不是M的路徑。

對任意π=e1…em(m≥2)∈P(M),記o(π)=c(e1)為π的開始狀態(tài),a(π)=δ(em)為π的終止狀態(tài)。又假設e1=(q1,σ11,…,σn1),e2=(q2,σ12,…,σn2),…,em=(qm,σ1m,…,σnm),則定義str(π)=(σ11σ12…σ1m,…,σn1σn2…σnm)。

當θ1,…,θn不全為ε時,

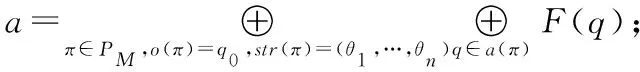
當θ1=…=θn=ε時,fM(θ1,…,θn)=F(q0)。

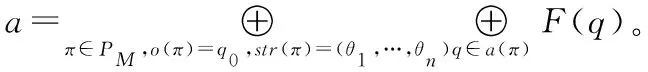
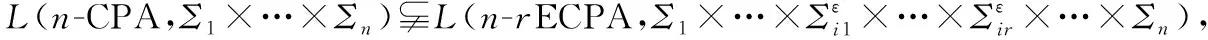
定理3的證明類似于定理1的,此處不再具體給出。

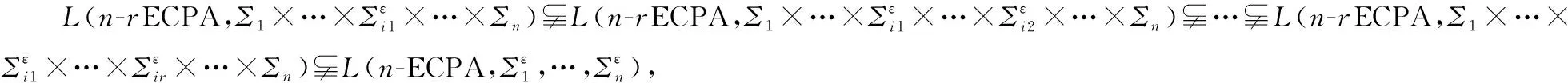
證明由n-rECPA和n-ECPA的定義可知定理顯然成立。

□

由定理3與定理4可得如下推論：

由以上定理與推論可知,n-CPAs、n-rEPAs和n-EPAs三者是不等價的。然而,下面將證明存在一類特殊的n-EPAs,其與n-CPAs是等價的。

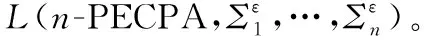
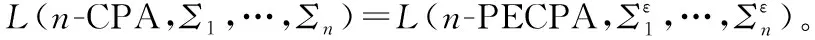
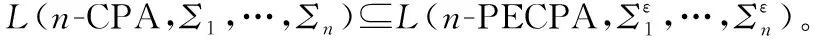
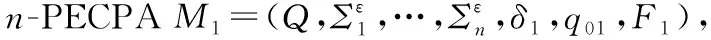
(i)q02=q01;

(iii)δ2:Q×Σ1×…×Σn→2Q,?q∈Q,σ1∈Σ1,…,σn∈Σn,δ2(q,σ1,…,σn)={p|p∈a(π),π∈PM1,o(π)=q,str(π)=(σ1,…,σn)}。

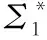
(1)若存在π2∈PM2,滿足str(π2)=(θ1,…,θn),則一定有|θ1|=…=|θn|,那么：

①當|θ1|=…=|θn|>0時,有:

fM2(θ1,…,θn)=

(1)

由(iii)可知,對任意的π∈PM2,且o(π)=q,str(π)=(θ1,…,θn),都存在一個π′∈PM1使得o(π′)=q,str(π′)=(θ1,…,θn),且a(π′)=a(π)。反之亦然。從而式(1)轉變?yōu)槭?2)所示：

(2)

又當π′2,π1∈PM1,o(π1)=q,q∈a(π′2)時,有π′2π1∈PM1,所以,式(2)轉變?yōu)槭?3)所示：

(3)

(2)否則,fM2(θ1,…,θn)=0=fM1(θ1,…,θn)。

□

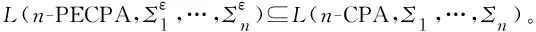
以上定理說明,即使n-ECPAs與n-CPAs并不是等價的,但卻有n-PECPAs與n-CPAs是等價的。

此外,由文獻[27]中的定理4.2可以推出,當n=1時,n-ECPAs與n-CPAs是等價的。由此也可以看出,狀態(tài)轉移函數在每個字符集上是否帶空轉移對n元偽加權有窮自動機接受語言的影響不同于其對偽加權有窮自動機的影響。

5 結束語

本文以不確定性數據世系分析中結果元組的概率計算為應用背景,引入了n元偽加權有窮自動機(n-PA)、帶r-型空轉移的n元偽加權有窮自動機(n-rEPA)、帶空轉移的n元偽加權有窮自動機(n-ECPA)、分明型n元偽加權有窮自動機(n-CPA)、帶r-型空轉移的分明型n元偽加權有窮自動機(n-rECPA)、帶空轉移的分明型n元偽加權有窮自動機(n-ECPA)、確定型n元偽加權有窮自動機(n-DPA)與一個特殊的帶空轉移的分明型n元偽加權有窮自動機(n-PECPA)及其對應語言的概念,探究了以上自動機之間的等價性關系,并得到以下結論:

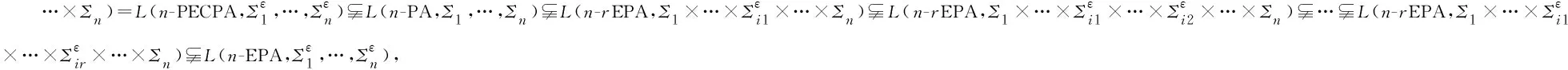
以上結論說明,狀態(tài)轉移函數在每個字符集上是否帶空轉移對n元偽加權有窮自動機接受的語言有著重要的影響,且不同于其對偽加權有窮自動機的影響。本文完善了偽加權有窮自動機理論,并為n元偽加權有窮自動機在不確定性數據處理中的應用奠定了理論基礎。下一步的工作將以本文研究為基礎探究n元偽加權有窮自動機在不確定性數據處理方面的具體應用。