壓電陶瓷驅動高頻噴射閥的結構設計

呂廣雷， 馬訓鳴*， 李峙毅， 陳勇潔

(1.西安工程大學 機電工程學院， 陜西 西安 710600；2.西安工程大學 西安市現代智能紡織裝備重點實驗室， 陜西 西安 710600)

噴氣織機具有運行車速快、生產效率高、物料消耗少、引緯方式合理，以及運轉操作安全、簡便[1]等優點，使噴氣織機成為市場上應用較廣、前景較好的無梭織機。噴氣織機的氣耗量占總能耗量的70%左右，輔助噴嘴占總氣耗量的80%左右[2]。由此可見對輔助噴嘴起控制作用的噴射閥的性能直接影響織機的引緯質量和能耗。國內廣泛應用的輔助噴嘴的控制閥是高頻電磁閥，不但依賴進口，價格昂貴，而且受電磁鐵本身的局限，響應頻率低，造成能源浪費。

目前，由于壓電陶瓷壓電性能優越、響應速度快和耐久性好的特點，使其成為精準控制閥的首選材料。國內外學者對壓電陶瓷驅動閥進行了深入的研究[3]。壓電陶瓷驅動閥以不同的結構特征分為：先導型、直動型、噴嘴擋板型和開關型等4類。楊慶俊等[4]提出一種采用壓電驅動器控制先導閥口開度的比例減壓閥，通過Simulink軟件分析了結構參數對閥的靜態特性的影響。俞軍濤等[5]提出了一種壓電直接驅動伺服閥，設計了一種新型的液壓微位移放大結構，對膜片結構進行了剛度和強度分析。彭暢等[6]提出了直動式噴嘴擋板式壓電伺服閥，建立了數學模型，對閥的動態特性進行仿真。宋敏等[7]提出的壓電高速開關閥，運用FLUENT對高速開關閥進行了動態流場分析。壓電驅動器常用的結構類型分為：壓電疊堆型，壓電雙晶片型等。解凱等[8]提出了一種疊堆式壓電微噴閥，建立微噴閥的多場耦合模型，進行動態性能影響仿真分析。黃燕[9]提出壓電先導型啟動閥，采用懸臂式壓電雙晶片驅動結構，并對閥的驅動結構進行了仿真分析。

為了提高噴氣織機的工作性能，減少能源消耗，課題組提出了一種基于壓電驅動技術的新型壓電噴射閥。通過ANSYS軟件，對壓電驅動器的靜態特性、閥體的流場等進行綜合分析,為壓電噴射閥的優化設計提供了參考依據。

1 壓電噴射閥的基本原理與系統建模

1.1 壓電噴射閥的基本原理

在傳統電磁閥的基礎上，課題組將電磁閥的驅動裝置改為壓電驅動器，如圖1所示。壓電噴射閥由電源、進氣口、出氣口、壓電彎曲片、凸臺、閥體、密封墊和開關等組成。壓電噴射閥采用噴嘴擋板式結構，擋板由壓電彎曲片組成。當電源開關斷開時，壓電彎曲片靠開關閥預緊力關閉進氣孔，停止工作。當電源開關閉合時，壓電彎曲片通電，電場方向與極化相同的一側產生位移收縮，另一側則產生位移伸長，使壓電彎曲片自由端產生位移，進氣口打開，進氣口與出氣口形成通路，壓電閥開始工作。

根據文獻可知常用的壓電驅動器有疊層式和雙晶片式2種結構。壓電疊層式驅動器的優點是對負載的輸出位移和輸出力大，響應時間短；缺點是驅動電壓高，位移小，需要位移放大機構配合使用。而壓電雙晶片式具有結構緊湊、驅動位移大和驅動電壓小等優點，但存在驅動力小的缺點。為了滿足壓電驅動器對力和位移的要求，選用pzt-5型號壓電彎曲片，其由10層厚度為0.1 mm的彎曲片燒結而成，結構示意圖如圖2所示。

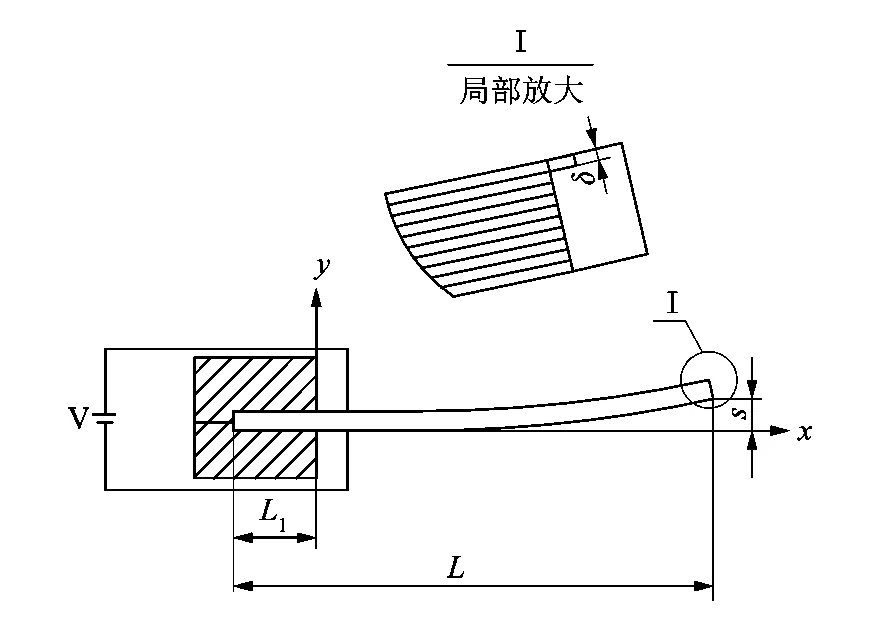
圖2 壓電驅動器示意圖Figure 2 Piezo electric driver schematic

壓電驅動器工作原理為：壓電彎曲片通電，電場方向與極化相同的一側產生位移收縮，另一側則產生位移伸長，使壓電彎曲片的自由端產生位移。位移S公式為[10]：

(1)

式中：L為壓電彎曲片長度，mm；d31為壓電常數，C/N；V為驅動電壓，V；δ為壓電彎曲片厚度，mm。

1.2 壓電驅動系統建模分析

如圖3(a)所示，壓電陶瓷的電路模型可以等效簡化為電阻R與電容C串聯的模型，將其視為慣性環節[11-12]；如圖3(b)所示，將壓電驅動系統簡化為質量、彈簧和阻尼系統[13]。根據電路平衡和力學平衡得：

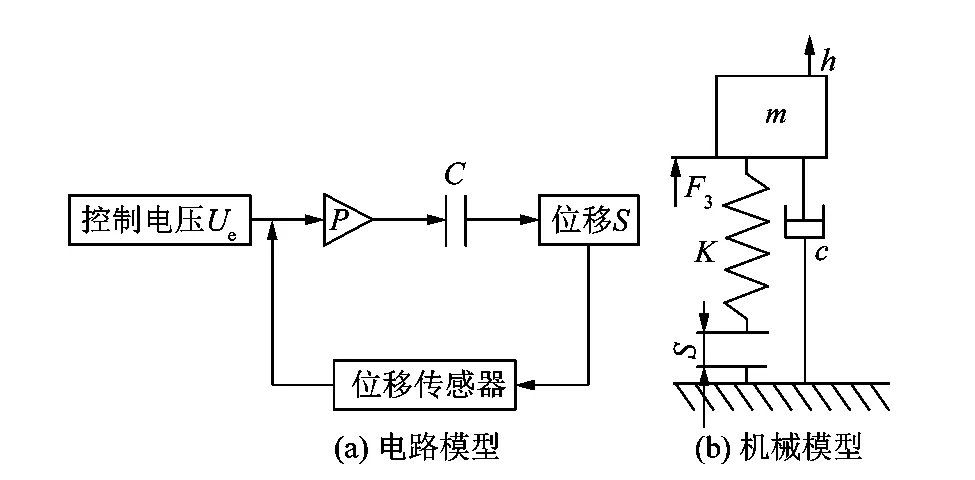
圖3 壓電驅動器的等效模型Figure 3 Equivalent model of piezoelectric driver

(2)

(3)

對式(2)和(3)進行拉普拉斯變換并整理得：

(4)

(5)

聯立式(4)和(5)得到輸入電壓、輸出位移的傳遞函數為：

(6)

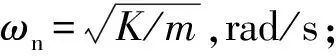
2 壓電噴射閥的主要結構參數設計計算

2.1 壓電驅動器的受力分析

作為壓電噴射閥的核心驅動部件，壓電彎曲片的參數和性能至關重要，由圖1(b)可知當壓電噴射閥停止工作時，進氣口關閉。為了防止壓電噴射閥氣體泄漏并使其工作穩定，對壓電彎曲片進行受力分析。

由圖1分析得到壓電噴射閥的受力模型為：

F1=F2+F3。

(7)

由胡克定律公式可得：

(8)

壓電彎曲片的剛度公式[14]為：

(9)

課題組選擇O型橡膠密封圈，密封圈預緊力[15]公式為：

(10)

擋板所受的氣流沖擊力主要由2部分組成：一部分為射流作用在擋板上的力；另一部分是控制腔的靜壓力作用在擋板上的液壓力[14]。由公式得：

(11)

式中：F1為壓電片的預緊力，N；F2為橡膠墊片對壓電彎曲片的支撐力，N；F3為進氣口的壓力，N；x為壓電彎曲片到凸臺平面的距離，mm。EP為壓電陶瓷彈性模量，GPa；δ為壓電彎曲片厚度，mm；p1為工作壓力，GPa；r1為進氣孔的直徑，mm；r2為凸臺直徑，mm；Cd為流量系數；h為工作間隙，mm。

2.2 壓電噴射閥進氣口的設計

壓電噴射閥在進口處的壓力p1為0.5 MPa，額定流量Q=20 L/min。壓電驅動器為擋板式結構，則根據流量公式[16]與r1有如下關系：

(12)

根據受力分析可知h工作間隙由2部分組成：一部分為壓電彎曲片驅動位移，另一部分為壓電彎曲片受到氣流力沖擊變形產生的位移。由公式得：

(13)

將式(11)和(13)聯立得工作間隙與進氣口直徑關系：

(14)

式中：Δp為壓差，GPa；ρ為空氣密度，kg/m3。

聯立式(7)～(11)可以得到剛度K與r1成正比，剛度K與壓電彎曲片的長度L成反比，L過長則壓電彎曲片的剛度減小，導致壓電噴射閥漏氣；L過短則導致壓電驅動位移短，無法滿足工藝要求。由式(11)和(12)可知壓電噴射閥額定流量Q與r1成正比，F3與r1成正比。r1過大時，F3將增大致壓電噴射閥漏氣，r1過小則無法滿足壓電噴射閥對流量的要求。為了保證壓電噴射閥的驅動位移，首先確定壓電彎曲片幾何尺寸，然后再確定進氣口r1的直徑。綜合考慮，設計壓電彎曲片的幾何尺寸為68 mm×20 mm×1 mm，單向驅動位移為1.5 mm，最大驅動力為24 N；r1為4 mm。滿足壓電噴射閥進口處的壓力P1為0.5 MPa和額定流量Q為20 L/min的工藝要求。

3 壓電噴射閥仿真

3.1 壓電彎曲片剛度性能仿真

3.1.1 壓電彎曲片剛度理論計算

將長度L為68 mm，寬度b為20 mm，厚度δ為1 mm，壓電陶瓷彈性模量EP為56 GPa代入式(9)，可以得到剛度K=7 123.9 N·m-1。

3.1.2 壓電彎曲片的剛度模擬仿真

建立壓電彎曲片的幾何模型，將幾何模型導入ANSYS的static structural模塊。導入的參數：L為68 mm，b為20 mm，EP為56 GPa，δ為1 mm，ρ為7 600 kg/m3，泊松比μm為0.36。在壓電彎曲片的一端進行固定約束，使之成為懸臂梁狀態，在自由端施加垂直方向負載F5=10 N，分析自由端的形變結果，得到形變結果X如圖4所示。

圖4 壓電彎曲片形變XFigure 4 Piezoelectric bending sheet strain X

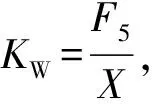
3.1.3 壓電彎曲片的液動力剛度計算

為了保證壓電彎曲片作為驅動器的高頻閥的穩定性，就必須保證壓電彎曲片的機械彈性剛度大于液動力剛度。

通過對式(7)求導可以求得液動力剛度[17]為：

(15)

根據工藝要求工作間隙h=1.5 mm，此時Ky取得最大值，Ky，max=6 785.8 N·m-1。

可得出結論：壓電彎曲片的機械彈性剛度KW=7 123.9 N·m-1大于壓電彎曲片的液壓彈性剛度Ky，max=6 785.8 N·m-1，保證了壓電彎曲片作為驅動器時的穩定性。

3.2 壓電高頻噴射閥流體仿真

由式(7)和(11)可得當r1與h增大時F3將增大，當F3大于F1時閥關閉狀態下會出現漏氣現象。而當r1過小時則無法滿足壓電噴射閥額定流量的要求；當間隙h較小時，出口的流速過小無法滿足供氣要求；當工作間隙h過大時，不但會降低閥的響應頻率，同時也會造成大量的壓縮氣體浪費。所以選擇合理的r1和h對壓電噴射閥的設計至關重要。

3.2.1 網格劃分

在FLUENT仿真中，網格劃分質量會直接影響計算的收斂和計算的準確性，為了流場的精確計算，對模型進行了合理簡化。在工作間隙等流場復雜區域進行局部加密，流場網格如圖5所示。

圖5 網格劃分Figure 5 Meshing

3.2.2 算法設置

根據計算，流場的雷諾系數Re>2 000，湍流模型選擇RNG的k-ε，速度與壓力耦合采用SIMPLE算法。保持計算精度，離散格式選擇二階迎風差分格式。

3.2.3 邊界條件設置

入口邊界設置為壓力進口，工作壓力設為0.5 GPa。面板設置包括進口壓力、湍流能和湍流離散率等；出口邊界設置為壓力出口，操作壓力設置為0 MPa；其余設置為壁面。

3.2.4 壓電噴射閥的流量分析

改變進氣口的工作間隙h的大小，工作間隙從0.3 mm依次增加到1.8 mm。進氣孔r1分別選擇3 mm，4 mm和5 mm。依據不同工作間隙和進氣口對流量的影響進行仿真計算，仿真結果如圖6所示。

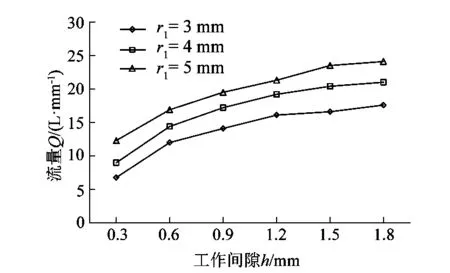
圖6 流量分析Figure 6 Flow analysis

從圖6中可以看出，在進氣口直徑r1一定的情況下，隨著工作間隙h的增加，壓電噴射閥的流量隨之增加，當h增大到一定值后，壓電噴射閥的流量增長趨勢減緩；在工作間隙h一定的情況下，壓電噴射閥流量隨著進氣口r1的增大而增大。由圖可知當r1=4 mm，h=1.5 mm時，流量達到20.4 L/min，與式(12)描述情況和結果基本一致，滿足工藝要求。

3.3 壓電驅動系統的時域仿真

阻尼比是反映系統時間響應和穩定性的重要指標，表現在壓電噴射閥的響應頻率和控制精度上。利用MATLAB軟件對壓電驅動器的系統模型進行變量為阻尼比B的階躍響應仿真 。

將阻尼比設為0.1到0.9進行仿真，圖7為阻尼比對系統穩定影響的階躍響應圖。從圖中可知，系統的調整時間和超調量隨著阻尼比B的改變而變化，當B增大時系統的超調量隨著B的增大而減小，當B=0.7時系統的超調量消失，壓電驅動系統穩定。壓電驅動器的階躍響應時間為2 ms，壓電驅動器的穩態輸出位移為1.45 mm。

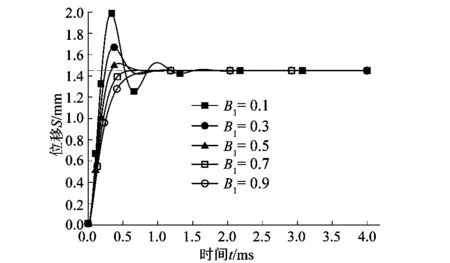
圖7 阻尼比對系統的影響Figure 7 Effect of damping ratio on system

通過以上仿真得出結論：當等效質量m為0.002 4 kg，剛度取7 N/mm，系統模型的阻尼比B取0.7時，系統保持穩定，且響應時間穩定于2 ms。一般國產噴氣織機引緯電磁閥的響應時間在5～8 ms內，設計的噴射閥響應速度相比高60%左右。

4 結論

課題組提出了一種應用于噴氣織機引緯的壓電噴射閥，對壓電噴射閥的結構參數進行設計，建立模型，并對其進行仿真研究。通過對壓電彎曲片剛度進行靜力學仿真與計算，得出了合理的噴射閥流體動力剛度。通過ANSYS的FLUENT流體分析模塊對壓電噴射閥的內流場進行分析，確定了壓電噴射閥的工作間隙，最后對壓電驅動系統的時域進行分析，確認壓電噴射閥具有良好的動態特性。結果表明：對比傳統電磁閥，響應速度提高60%左右，無用氣體消耗可減少約50%，達到節能的同時也為壓電噴射閥后續機構優化提供了良好的基礎和參考。