類水滴型擾流元順排式矩形微通道的流動換熱性能研究*

侯娜娜，張 東，李樹謙，張 猛

（1.河北水利電力學院土木工程系，河北 滄州 061001；2.河北科技大學建筑工程學院，河北 石家莊 050018；3.河北省數據中心相變熱管理技術創新中心，河北 滄州 061001；4.滄州市儲熱及低品位余熱利用型電磁供熱技術創新中心，河北 滄州 061001）

隨著科技水平的提升及工業現代化的快速發展，越來越多的領域散熱問題日益突出，如數據中心、電子芯片冷卻、5G 基站等[1]。為解決日益突出的電子器件散熱問題，國內外研究學者已開展了大量關于通過增加擾流結構或改變擾流結構形式等方法進而增強對流換熱效果的研究。

CHEN 等[2]研究了宏觀尺度下流動工質為空氣的類水滴型順排擾流元的矩形通道的流動換熱性能，并發現在雷諾數Re變化范圍為900～9000 時，水滴型擾流元結構散熱性能要優于圓形擾流元結構。譚曉茗等[3]進行了宏觀尺度下流動工質為空氣的水滴形和圓形叉排擾流柱陣列矩形通道內流動和換熱的數值模擬，發現水滴形比圓柱形擾流的強化換熱效果約下降15%，但流動阻力卻下降了近50%。王奉明等[4-6]對宏觀尺度下不同形狀擾流柱叉排陣列的矩形通道空氣流動過程進行了試驗和三維數值模擬，分析了擾流柱形狀和來流Re數對換熱特性的影響，并對其強化換熱特性和壓力損失特性進行了對比分析，發現水滴形擾流柱群矩形通道的綜合性能最佳。

楊超、張高高等[7-8]通過數值模擬方法對微觀尺度下流動工質為水的變密度凸肋通道及改變水滴型尾緣角度通道的流動和換熱特性進行了研究，在Re=100～600 時，水滴型肋片換熱性能優于圓形肋片并隨尾翼長度增加而增強。前述調研發現，以往學者對于類水滴型擾流元換熱性能的研究主要集中在宏觀尺度或流動工質為空氣的工況下，而對于微觀尺度并且流動工質為水的工況下類水滴型擾流元的流動換熱性能研究較少。為此，本文設計了類水滴型順排式擾流結構的矩形微通道并對其流動換熱性能進行了數值模擬研究。

1 物理模型

本數值模擬采用的物理模型主要分為3 個部分，即入口緩沖區域、擾流流動區域、出口緩沖區域，其長度L1、L2、L3分別為2.0 mm、15.8 mm、2.2 mm，矩形微通道總長度為20 mm，通道高度為0.2 mm，寬度為3 mm，矩形微通道厚度為0.2 mm。矩形微通道內擾流元為類水滴型，其高度與矩形微通道高度相同。通道內共5 排類水滴型擾流元，每排共16 個擾流元，且擾流元采用順排布置方式。矩形微通道材質為鋁，通道內的流體為去離子水。矩形微通道內擾流元的布置及流體流動方向如圖1 所示。

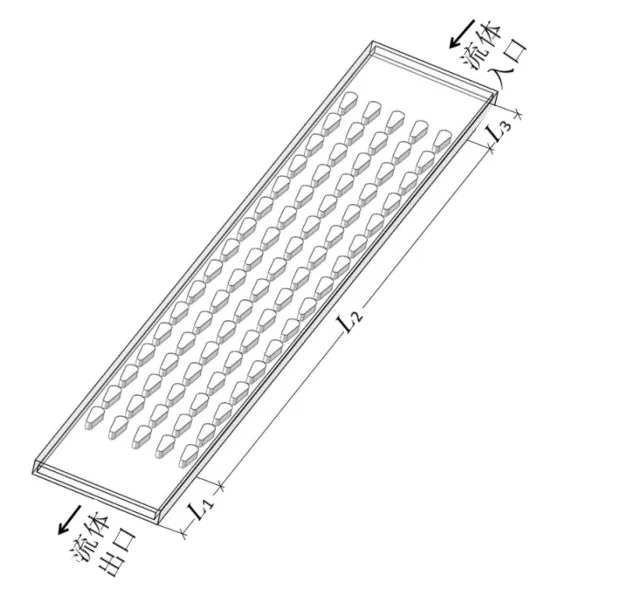
圖1 矩形微通道內擾流元的布置及流體流動方向

矩形微通道內類水滴型擾流元布置為對稱結構，擾流元的大圓半徑為0.15 mm，小圓半徑為0.08 mm，兩圓間距為0.50 mm。擾流元間的橫向距離為0.6 mm，水流方向距離為0.5 mm（二者均為圓心間距）。相鄰兩排擾流元間橫截面形成了漸縮漸擴流道，橫截面最小間距為0.3 mm，最大間距為0.45 mm，與矩形微通道側壁面相鄰的擾流元間的流道橫截面最小間距為0.15 mm，最大間距為0.23 mm。

2 數學模型

文獻[8]提出了區別于常規通道的水滴型微通道內流動換熱的數值模擬方法，參照其提出的數值模擬方法，認為本模型中工質為不可壓縮流體，物性參數為常數不隨溫度變化，熱輻射作用忽略不計，計算區域采用層流模型，考慮表面張力的影響，壓力速度耦合采用SIMPLE 計算方法。

3 邊界條件

本模擬主要研究流體入口速度改變時類水滴型順排式微通道的換熱性能，入口邊界條件為給定速度及溫度，出口邊界條件為自由出流，矩形微通道底面為恒定熱流加熱壁面，速度無滑移，其他壁面均為絕熱壁面。矩形微通道邊界條件設置的具體內容如下：入口流體流速為0.2 m/s、0.4 m/s、0.6 m/s、0.8 m/s 和1.0 m/s，入口流體溫度為300 K，加熱壁面熱流密度為300 kW/m2。

4 網格劃分與驗證

采用多面體網格對計算區域進行網格劃分，在擾流元與流體接觸面附近采用curvature 和proximity方式進行網格加密。網格劃分示意圖如圖2 所示。

圖2 矩形微通道的網格劃分示意圖

為確保數值模擬的計算時間和準確度而進行了3組數據的網格無關性驗證。網格數分別389685、494890、607389。在入口流速為0.2 m/s 時，進出口溫差及壓降的誤差分別為3.08%、1.31%和2.75%、1.53%。通過誤差比較，發現網格數為494890 時較為合適。

5 數據處理

文獻[8]對水滴型擾流元矩形微通道的水力直徑D、對流換熱系數h、雷諾數Re、努塞爾數Nu及摩擦阻力系數f等進行了較為詳細的說明。本文采用矩形微通道類水滴型順排結構進行流動傳熱分析，與文獻[8]十分相似，故本文采用文獻[8]相應公式進行數據處理。

6 結果與討論

圖3 為入口流速0.6 m/s 時矩形微通道內速度、溫度及壓力的分布云圖。矩形微通道內流體速度整體呈現增長趨勢。由入口緩沖區域進入擾流流動區域時，在擾流元通道內的流體流速有明顯的增加，其主要原因在于通道橫截面突然變小，形成了噴管結構，流體流動滿足噴管截面變化規律，當截面突然變小時，其流速增加。

圖3 矩形微通道速度、壓力、溫度分布云圖

此外，擾流元通道內的流體速度沿流動方向逐漸增加，主要是由于相鄰兩排擾流元間的橫截面以漸縮—漸擴—漸縮的規律進行變化，從而使得流體速度逐步疊加。隨后擾流流動區域末端較高速度的流體在出口緩沖區進行較為平緩的匯合，相較于擾流流動區域流體速度有所降低。

矩形微通道內溫度變化趨勢與速度變化趨勢相似，均沿流動方向逐漸增加。流體溫度在入口緩沖區溫度最低，約為302 K，在出口緩沖區溫度最高，約為322 K。類水滴型擾流元溫度在擾流區域第1 列溫度最低，約308 K，在第14 列溫度最高，約為324 K。雖然流體在流動過程中速度在逐漸增加，但流體在流動過程中不斷與加熱壁面進行熱量交換，從而流體溫度隨流動不斷增加。與之相對應的是在擾流流動區域末端流體帶走熱量的能力與起始端相比較弱，故在恒定加熱壁面條件下，擾流流動區域末端擾流元溫度高于起始端擾流元溫度。

與圖3（a）和圖3（b）相比較，圖3（c）中所示的不同之處在于微通道內壓力是逐漸降低的，并且在入口緩沖區域及出口緩沖區域壓力降低較為平緩，而在擾流流動區域壓力降低較為明顯。擾流區域末端壓力與始端相比降低了約8 kPa，其原因主要是由于擾流元的布置及微通道長度明顯長于其他兩個區域，使得擾流流動區域的沿程阻力，特別是局部阻力均高于其他區域。

圖4 為不同雷諾數Re下的微通道進出口壓降變化趨勢。由圖可見，隨著Re的增大，壓差隨之變大且基本呈線性變化，其主要原因是由于入口流速增加導致微通道內沿程阻力和進出口處局部阻力均增大所致。

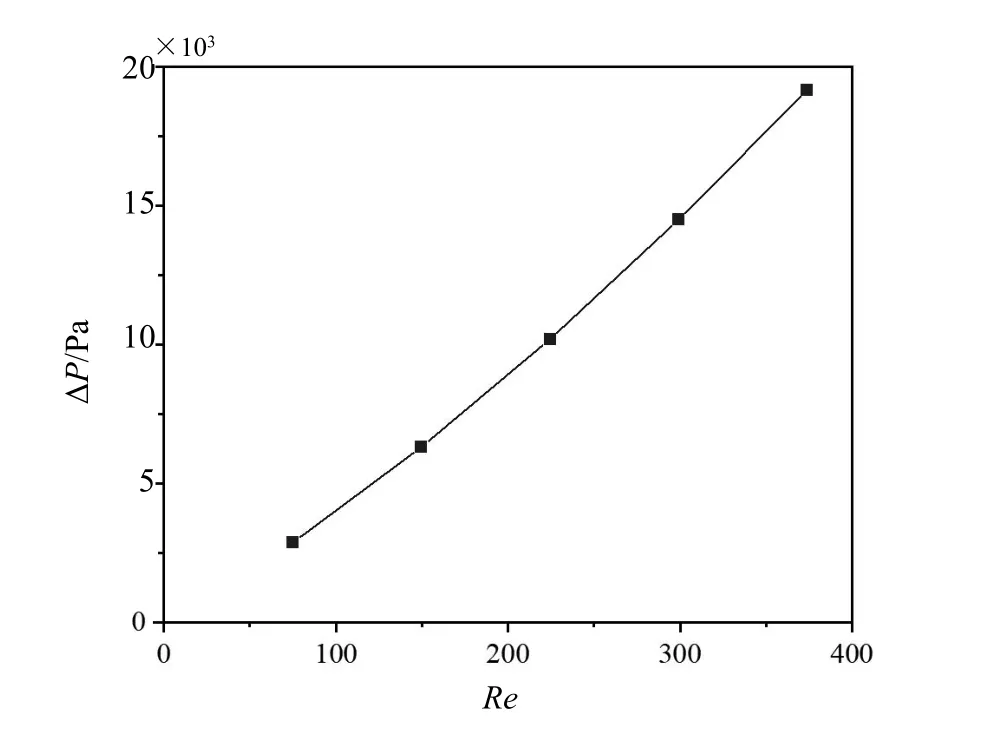
圖4 微通道進出口壓降隨雷諾數變化情況

圖5 和圖6 分別為不同雷諾數Re下的平均對流換熱系數和平均努塞爾數變化情況，隨著雷諾數Re的增大，平均對流換熱系數和平均努塞爾數均呈增加且增加趨勢基本一致。由公式可以看出，微通道水力直徑與導熱系數為定值（假設導熱系數為常數），故平均對流換熱系數和平均努塞爾數變化趨勢基本一致。雷諾數Re增大導致平均對流換熱系數增加的主要原因可能是雷諾數Re增大會使流體流動邊界層厚度和熱邊界層厚度減小，進而使得平均換熱系數增加。

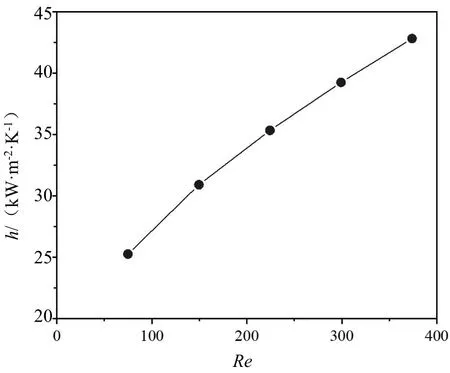
圖5 平均對流換熱系數隨雷諾數變化情況

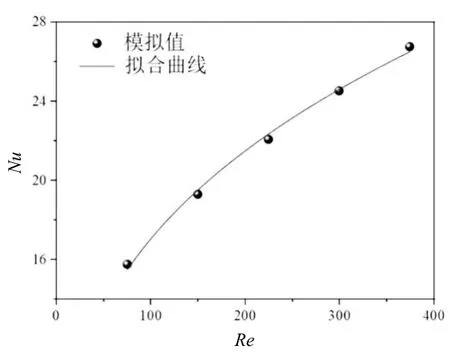
圖6 平均努塞爾數隨雷諾數變化情況

利用最小二乘法，獲取了矩形微通道類水滴型擾流元順排布置且雷諾數Re處于74～375 時，雷諾數與平均努塞爾數的關系式，即Nu=3.68289Re0.33312。

7 結論

本文考察了不同雷諾數下類水滴型擾流元順排式矩形微通道的流動和傳熱特性，主要結論概括如下：①隨著雷諾數Re增加，微通道內的壓降、平均對流換熱系數及平局努塞爾數均呈現增加趨勢，且平均對流換熱系數及平局努塞爾數增加趨勢基本一致。其主要是由于流速增加使得進出口沿程阻力和微通道內沿程阻力增大，從而導致微通道進出口壓降增大，此外雷諾數的增加導致流體流動邊界層厚度和熱邊界層厚度減小，進而強化了換熱。②定量研究發現，在入口流速范圍為0.2～1.0 m/s 的情況下，矩形微通道的壓降約為2.8 ～19.2 kPa，平均換熱系數約為25.25 ～42.83 kW/（m2·K），平均努塞爾數約為15.78～56.77。③進一步理論分析表明，當雷諾數Re取值在74～375范圍內時，雷諾數與平均努塞爾數存在以下關系，即Nu=3.68289Re0.33312。