基于SIR-MCMC 方法的新冠肺炎疫情評估與防控

周潛，歐宜貴，鄧新春，黃振，黃玉蘭

（1.湖南工業職業技術學院基礎課部，湖南 長沙 410000；2.海南大學理學院，海南 海口 570228）

當前，我國處在對新冠肺炎疫情內防擴散、外防輸入的重要階段。因我國新冠肺炎疫情較早出現在湖北省，文章研究湖北省的新冠肺炎疫情相關數據，評估其發展進程和不同防控措施的效果，對未來有針對性地確定防控措施及資源調配提供參考。

目前，眾多學者針對各類疫情展開了廣泛的研究，其主要研究方法可分為四類。第一，基于確定性SIR 動力學模型思想的應用研究。喻孜等對經典SIR 模型進行修正，利用時變參數對新冠肺炎疫情發展進行預測，并分析了防控措施對疫情發展的影響［1］；Yang et al.應用SEIR 模型，采用多重擬合確定模型參數，對新冠肺炎疫情發展進行了綜合預測［2］；Tang et al.基于新型冠狀病毒的臨床特征、傳染性特征以及相關干預措施，對倉室模型進行了拓展，證明強化密切接觸者的追蹤、隔離可有效降低新冠肺炎疫情的傳播風險［3］；Jia et al.基于SEIR 模型，針對我國對新冠肺炎疫情的群體隔離政策進行了建模，說明了隔離措施的有效性和必要性，同時分析了疫苗介入對疫情控制的影響［4］。第二，基于隨機性傳染病模型思想的應用研究。Gray et al.基于感染者數量建立隨機微分方程，將經典的SIS 模型拓展到了隨機模型［5］；Clancy 基于感染周期非指數分布的前提假設，構建了一個分段馬爾可夫鏈模型，并用鞅推斷出了傳染病幸存者數量和感染者軌跡下的聯合分布［6］；徐寶春以SARS 為研究對象，對比研究了確定性SIR 模型和隨機性SIR模型［7］。第三，基于指數增長模型的應用研究。各學者采用指數增長模型分析新冠肺炎疫情發展及防控工作進展［8-10］。第四，基于統計學模型的應用研究。各學者挖掘新冠肺炎疫情的小樣本數據預測評估總體［11-12］。

確定性SIR 動力學模型邏輯清晰，在實際中被廣泛應用，但其忽略了病毒傳播過程中的隨機因素，僅探究整體發展規律，而實際情況中，新型冠狀病毒的傳播存在一定的隨機性，且病毒感染、恢復或死亡數量都是以人員個體為單位，并非確定性SIR 動力學模型所假設的各群體數量連續性變化，同時，基于隨機性傳染病模型思想的新冠肺炎疫情應用研究較少。文章沿用經典SIR 倉室模型的理念，各群體數量的變化以人員個體為單位，將各類人群的數量視為隨機變量，應用馬爾可夫鏈蒙特卡羅方法（MCMC）［7，13］模擬新型冠狀病毒在不同倉室進行轉移的可能性，記為SIR-MCMC方法，以此評估湖北省新冠肺炎疫情發展進程和防控措施效果。

1 模型描述

1.1 模型建立

經典SIR 倉室模型［14］116-117將人群分為易感者、感染者和移出者三類，并假設疾病傳播期內，所考察地區的總人口不變，假設β為單位時間內感染者傳染易感者的概率，簡稱感染強度，γ為單位時間內從感染者變為移出者的概率，即移除率。

在以下三種假設條件下，文章沿用SIR 倉室模型來研究新型冠狀病毒的傳播：新型冠狀病毒傳播期內，我國政府及時采取管控措施，有效地控制了人員流動，故在忽略自然死亡及出生等因素的前提下，假設傳播期內湖北省總人口不變；雖一旦成為疑似或確診人員，就會被政府迅速隔離，但考慮到管控期間的大范圍人際流動少，多為家庭內或小范圍內的人際頻繁流動，故假設新增確診病例均由已確診病例感染；考慮到新型冠狀病毒二次感染情形相對較少，為了便于研究，這里假設患者康復后再次被感染的概率為0。

文章記S（t）為t時刻正常且易感的總人數，I（t）為t時刻現有確診人數，R（t）為t時刻已經治愈和治療過程中死亡的總人數，對應SIR 模型的三類人群。將S（t）、I（t）、R（t）當作取值為非負整數的隨機變量，沿用經典SIR 模型的基本假設，假定S（t）+I（t）+R（t）=N，只研究其中兩個隨機變量即可，那么可將{S（t），I（t），t≥0} 視為二元隨機過程來研究，設該隨機過程是時齊的馬爾可夫鏈［13］，其聯合概率函數記為：

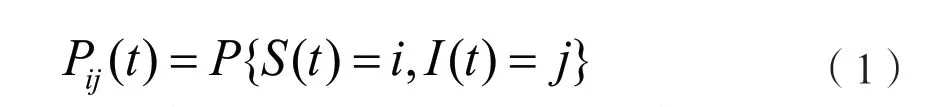
由經典SIR 模型的假設可知，當時間間隔Δt足夠小時，至多發生一次狀態轉移，故轉移概率的具體形式如下：

1.2 參數處理及模型求解

自2020 年1 月21 日開始，國家衛生健康委員會公布每日全國新冠肺炎疫情數據。文章樣本數據選自2020 年1 月21 日至4 月26 日的湖北省新冠肺炎疫情數據，主要采集累計確診人數、新增確診人數、累計治愈人數、累計死亡人數等信息，數據來源于國家衛生健康委員會及湖北省衛生健康委員會官方網站①中華人民共和國國家衛生健康委員會官網：http：//www.nhc.gov.cn；湖北省衛生健康委員會官網：http：//wjw.hubei.gov.cn。。

對模型進行求解，首先確定參數取值，湖北省人口約6 000 萬，因衛生管控措施影響，感染者真正能接觸到的易感者人數未知，即S（0）未知，將2020 年1 月21 日定義為初始日，則確診人數的初始值I（0）=338，假定R（0）=0，則三個待估參數分別是移除率γ，感染強度β和易感者初值S（0）。

1.2.1 估計移除率

圖1 不同β 與S（0）組合下的SSE

圖2 對比了確診人數模型擬合值與實際觀測值，不難發現，基于SIR-MCMC 的隨機模型較好地擬合了確診人數的發展變化。

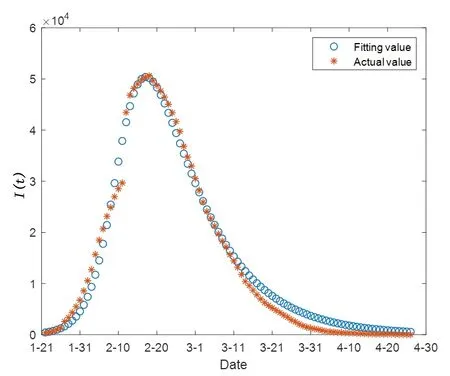
圖2 確診人數擬合值與實際觀測值對比

2 新冠肺炎疫情評估與防控

為評估新冠肺炎疫情發展進程及不同防控措施的效果，文章結合上文的已估計參數，分別從基礎再生數、t時刻現有確診人數可靠性、感染強度β、移除率γ和疫苗介入這五個方面來分析。

2.1 基礎再生數

發展初期，基礎再生數是用于預估新冠肺炎疫情是否可能暴發的重要指標，據SIR-MCMC 方法計算的參數估計值β=0.000 003，S（0）=114 000，結合γ=0.077，不難得出樣本所屬疫情階段的基礎再生數R0：

這表明每個感染者在其患病期內有可能感染4.441 6 個易感者，政府綜合管控的壓力較大，必須采取嚴格的綜合防控措施。

為刻畫新冠肺炎疫情發展進程及防控措施效果，結合已估計參數，基于SIR-MCMC 模擬出S（t）序列，同理可根據如下公式，計算新冠肺炎疫情發展過程中的有效再生數Rt：

據模型假設可知，易感者人數隨時間增加而減少，故有效再生數呈下降趨勢，具體趨勢如圖3 所示。2020 年2 月17 日、18 日的有效再生數分別為1.018 3、0.875 5，即2020 年1 月21 日至2 月17 日，有效再生數大于1，表明新冠肺炎疫情規模持續擴大；自2020年2 月18 日開始，有效再生數小于1，即每個感染者在之后預期感染的平均易感者人數小于1，表明我國政府嚴格的防控措施效果逐漸顯現，疫情逐步得到控制，較好地吻合了實際觀測值的變化。

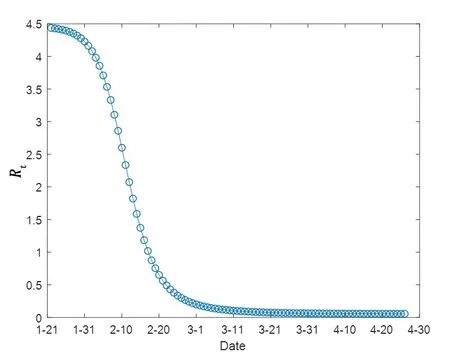
圖3 有效再生數

2.2 評估t 時刻現有確診人數

文章為便于掌握疫情觀測數據的可靠性，采用SIR-MCMC 方法，結合已估計參數，模擬1 000 條I（t）散點圖，易得I（t）的均值、標準差、頻率分布等統計信息。因確診人數的觀測數據受諸多因素影響，離散程度偏大，不宜采用基于置信度的置信區間來衡量，故采用偏離均值n倍標準差的形式來描述I（t）。表1 截取了2020年3 月1 日—9 日的確診人數相關指標，據此可知，I（t）的實際觀測值均處在偏離均值2 倍標準差的區間內，其中大部分處在偏離均值1 倍標準差的區間內，說明實際觀測值的可靠性較好。

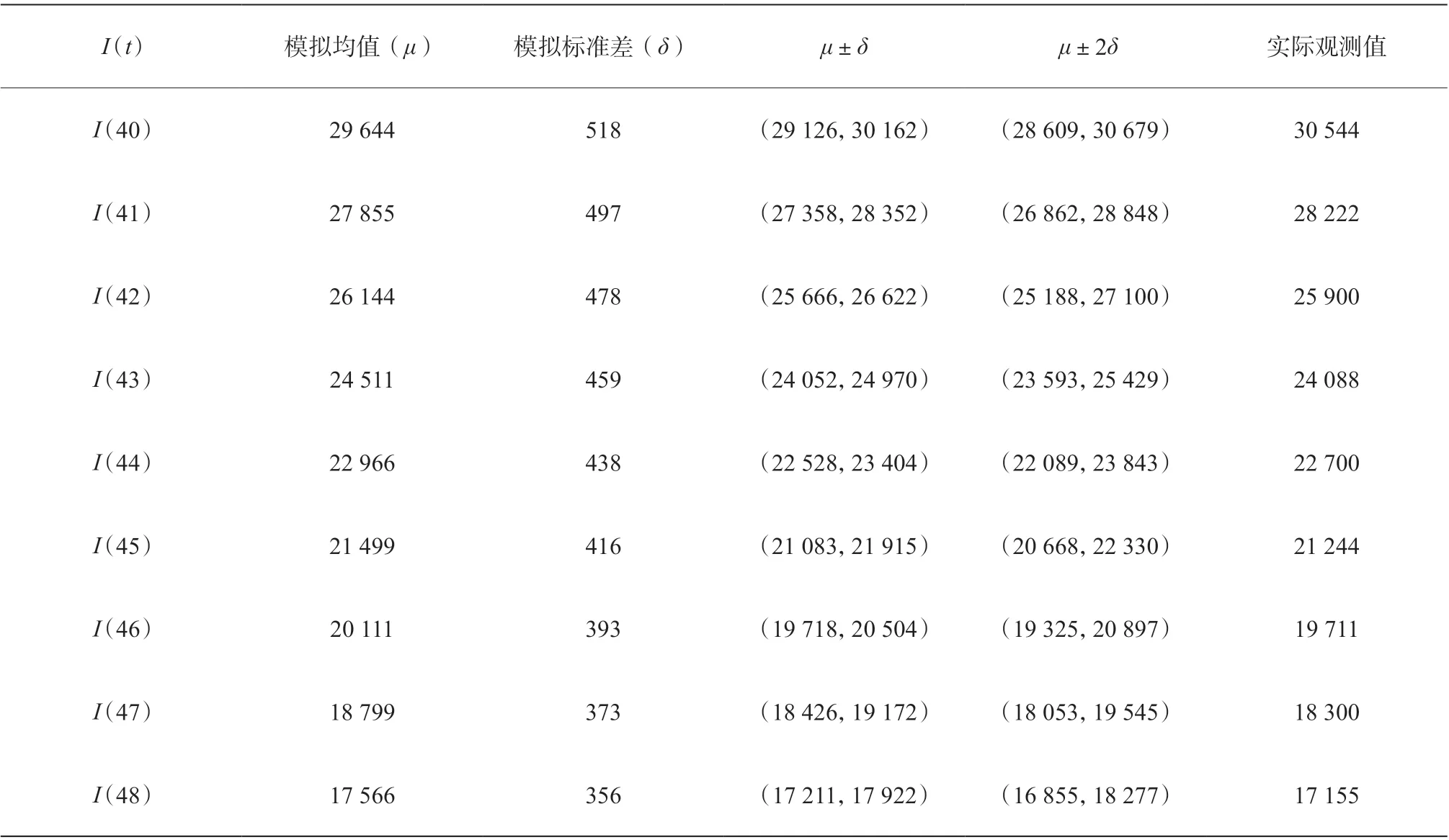
表1 t 時刻現有確診人數相關指標

2.3 感染強度β 分析

感染強度β是影響病毒傳播的重要因素，現有確診人數是防疫措施制定及醫療資源調配的重要參考指標，為衡量β改變對確診人數影響的數量化程度，假定其他參數均不變，僅將β分別降低20%、50%，分別對其采用SIR-MCMC 模擬1 000 條I（t）散點圖，并取t時刻的均值作為確診人數的擬合值，對比不同β下，確診人數隨時間的變化情況。如圖4所示，相比原模型，且β降低20%、50%時，確診人數峰值分別下降了17.56%、56.39%，抑制效果均較明顯，同時推遲了峰值時間，緩解了衛生防疫壓力，而β降低時，基礎再生數變小，新冠肺炎疫情也更易得到控制。這表明降低感染強度β的措施有利于對新冠肺炎疫情的控制，也有利于對醫療壓力的緩解，具體措施包括重點提高衛生防疫水平，提高篩查率，早隔離、早治療，保護一線醫務人員等高危易感群體。

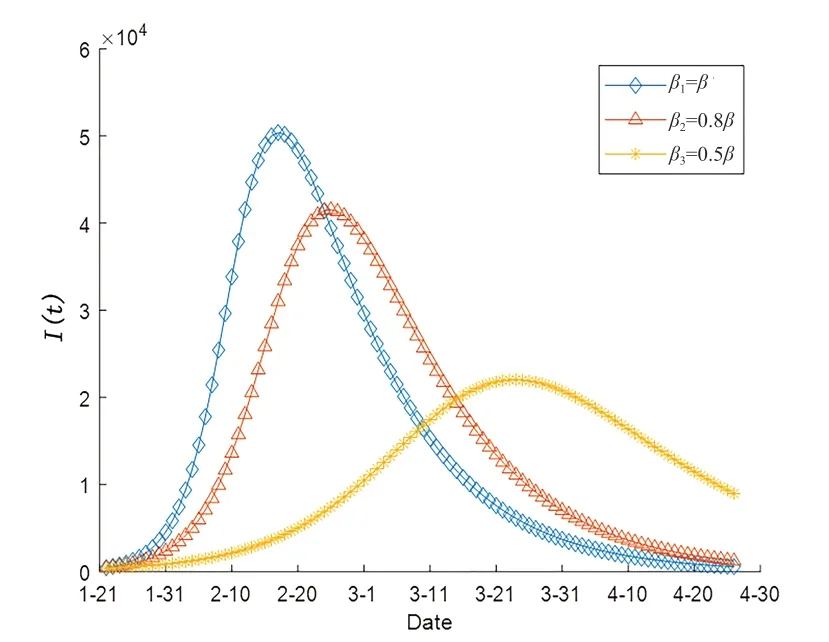
圖4 β 改變下的確診人數動態

2.4 移除率γ 分析

為衡量γ改變對確診人數影響的數量化程度，同樣假定其他參數均不變，僅對γ分別增大20%、50%，對比不同γ下，確診人數隨時間推移的變化情況。如圖5 所示，相比原模型，當γ增大20%、50%時，確診人數峰值分別下降了14.28%、32.48%，抑制均較明顯，峰值時間變化不大，且γ增大時，基礎再生數變小，新冠肺炎疫情更易得到控制。這表明增大γ的措施，同樣有利于對新冠肺炎疫情的控制，也有利于對醫療壓力的緩解，具體措施包括重點提高治療水平，同時防治并發癥。

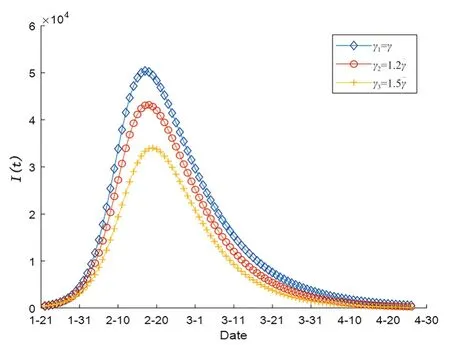
圖5 γ 改變下的確診人數動態

2.5 疫苗介入分析

為衡量疫苗介入對確診人數影響的數量化程度，同樣假定其他參數均不變，將疫苗保護率從0%分別提高到20%、50%，即易感人群分別下降20%、50%，對比不同疫苗保護率下，確診人數隨時間的變化情況。如圖6 所示，相比原模型，當疫苗保護率為20%、50%時，確診人數峰值分別下降了33.94%、77.82%，抑制非常明顯，同時推遲了峰值時間。這表明較大面積接種疫苗，對防控新冠肺炎疫情是非常有效的。

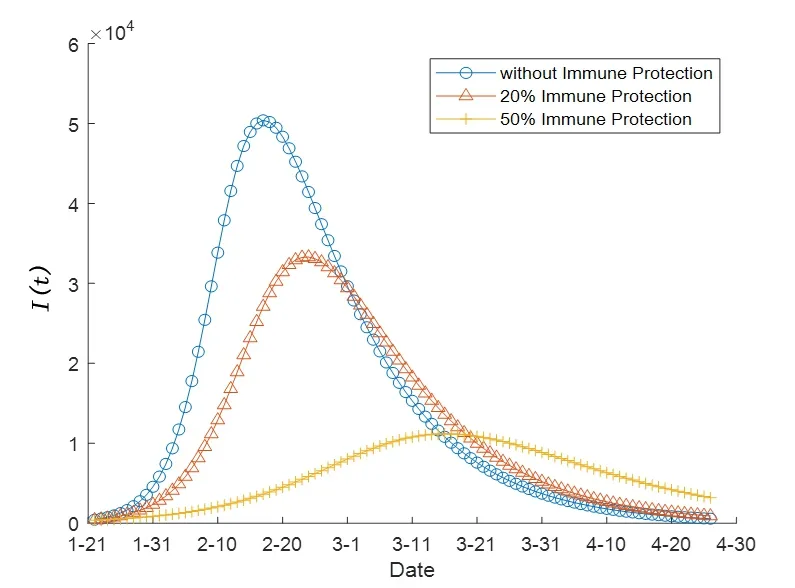
圖6 不同疫苗保護率下的確診人數動態

3 結語

文章基于SIR-MCMC 方法，采用實時數據擬合得出湖北省新型冠狀病毒感染強度β=0.000 003，易感者初值S（0）=114 000，較好地吻合了實際數據，同時從五個方面研究了湖北省的新冠肺炎疫情發展和不同防控措施的效果，得出如下結論及建議。

（1）湖北省新型冠狀病毒的基礎再生數為4.441 6，必須對其采取嚴格的綜合防控措施。自2020 年2 月18 日開始，有效再生數小于1，政府嚴格的防控措施效果逐漸顯現，疫情逐步得到控制。

（2）通過模型仿真數據驗證了t時刻現有確診人數的可靠性，此方法亦可用于預測。

（3）降低感染強度β、增大移除率γ以及疫苗介入的措施，均有利于對新冠肺炎疫情的控制，有利于對醫療壓力的緩解。當β降低20%、50%時，確診人數峰值分別下降了17.56%、56.39%；當γ增大20%、50%時，確診人數峰值分別下降了14.28%、32.48%；當疫苗保護率為20%、50%時，確診人數峰值分別下降了33.94%、77.82%。