一種Web三維地形表面積測量方法

廖洋洋, 陳建華, 張 倩, 劉 帥, 粟 解

(1.成都理工大學 地球物理學院，成都 610059；2.阿壩州自然資源與科技信息研究所，汶川 623000)

0 引言

傳統的地形測量由于其自身的局限且存在高危險性的隱患，在一些人不能到達的區域無法進行測量。隨著地理信息技術與互聯網技術的快速發展，三維實景地形模型已經能夠在瀏覽器中呈現。在瀏覽器中最受歡迎的三維地理信息庫是Cesium，它通過JavaScript封裝的三維地理信息可視化的庫，內部有大量的接口方便使用。三維WebGIS受到了越來越多的關注，其中對地形測量是其中的一個熱點。Michael等[1]使用新的Web技術(如HTML5、WebGL)，實現高效的客戶端分析，旨在推動基于Web的3D地理空間分析發展；Leila等[2]考慮到計算地形可見性問題，概述了在規則網格和不規則網格解決地形表面的算法；王恒[3]基于Cesium對地方大地測量平臺數據庫進行設計，提供了三維大地測量數據的展示、定位和查詢；范俊甫[4]對Cesium框架多源電子地圖瓦片方案進行設計，為地理信息系統與遙感技術項目應用提供了一種高靈活、低成本的解決方案；朱栩逸等[5]在GIS框架和Web服務的基礎上，提出了一種基于Cesium的三維WebGIS搭建方案，并簡單地實現了繪制功能；李偉等[6]使用ArcGIS軟件的三維分析功能，通過建立數字高程模型，使用不規則三角網(TIN)，對鄱陽湖洪水淹沒面積進行測量。

上述研究取得了較好的效果，但是目前的方法還無法滿足Web環境下三維地形面積測量的現實需求。這里以三維開源地理信息庫(Cesium)和地形切片技術為基礎，重點針對真實三維地形模型的表面積測量進行研究，為地形測量提供一種有效、可靠的測量手段。

1 系統架構

系統架構圖見圖1。采用瀏覽器到服務器再到數據層的方式獲取基本數據。根據Cesium官方文檔說明，加載的地形格式數據可以為.terrain格式，使用CesiumLab開源工具，可以將數字高程數據格式轉換為Cesium能識別的.terrain數據格式。使用IIS發布地形數據，Cesium內置有讀取加載.terrain的方法，使用CesiumTerrainProvider方法可以加載已經發布的地形數據。將遙感影像數據使用Geoserver數據進行發布，使用Cesium內置imageryProvider方法加載發布好的影像數據，以便在有起伏的影像數據上繪制需要測量的區域。Cesium內置有許多方便的接口供我們使用，其中提供的接口方法sampleTerrainMostDetailed，可以快速地獲取任何分辨率下地形切片任意一點最大精細程度的高度，而不必重新寫一種前后端交互的新方法，也不需要后端操作DEM方法，這一種專門讀取.terrain的方法，考慮到實現的復雜程度，所以采用前端計算的方式來實現整個算法，該方法主要針對Cesium提供一種計算思路。

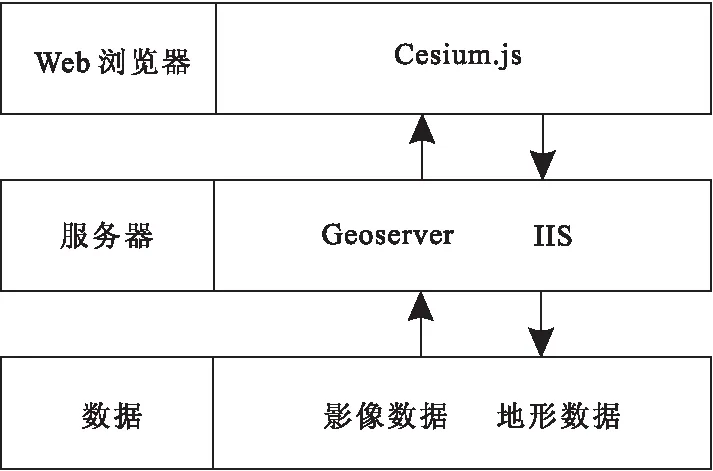
圖1 系統架構

2 具體算法

2.1 算法流程

算法的整體流程如圖2所示，通過繪制需要測量的區域，可以得到一個任意形狀多邊形，將多邊形分解成為多個三角形，使用雙線性插值的方法分別在每個三角形的最小邊界矩形中插值，每個三角形各自判斷插值過后的哪些點在自己內部，排除掉不在自己內部點，然后獲取各自內部點的高度，將這些在內部的點重新連接起來構成新的三角網，從而計算每個小三角形的面積，以此類推，直到分割過后所有的三角形都計算完面積，最后累加求和，得到整個區域的面積。

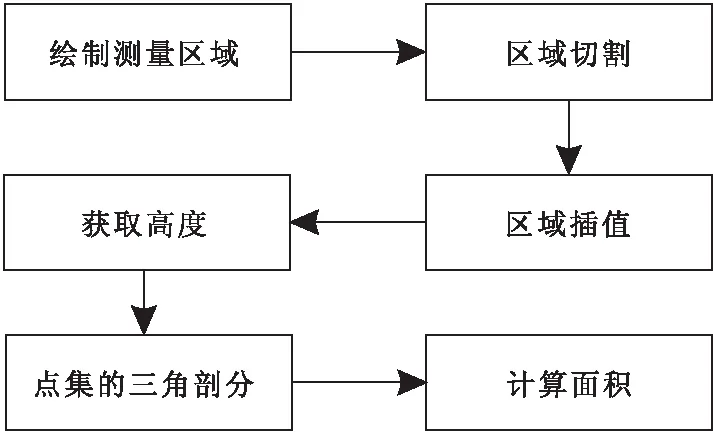
圖2 算法流程

2.2 區域切割

利用Cesium的ScreenSpaceEventHandler方法，用來捕捉我們繪制區域的事件。考慮到繪制的區域可能是任意形狀的多邊形，這里使用耳切法(Ear Clipping)對區域進行切割。

耳切法：連續頂點V1、V2、V3組成的內部不包含其他任意頂點的三角形，將其稱為簡單多邊形的耳朵(內角小于180°)[7]。V1與V3之間連接的線段稱之為多邊形對角線，點V2稱為耳朵頂點。雖然可以認為三角形任何一個頂點都能是耳朵，但是原理上認為一個三角形只有一個耳朵。一個由4個以上頂點組成的多邊形至少有2個不重疊的耳朵。根據這個理論特性，可以利用遞歸思想來解決三角形切割的方法。針對包含由n個頂點組成的簡單多邊形，找到其第一個耳朵，移除該耳朵頂點，此時剩余頂點將組成一個n-1個點的多邊形。重復這個操作，直到剩余三個頂點，遞歸結束。

2.3 區域插值

若繪制區域不是三角形則區域切割后會形成至少兩個以上的三角形，對每個三角形求取最小邊界矩形。最小邊界矩形是以三角形三個頂點(xk，yk)為基準，尋找出xmin、ymin、xmax、ymax4個值，然后以(xmin，ymin)、(xmin，ymax)、(xmax,ymax)、(xmax,ymin)4個點構成最小邊界矩形。

當獲取到每個三角形最小邊界矩形的時候，使用線性插值方法，對每個最小邊界矩形進行等間距插值。線性方程即線性插值的核心，使用線性插值的原因是因為其操作簡單，并且能均勻地對地區進行插值覆蓋。其已知兩個點的坐標(x0，y0)與(x1，y1)，假設存在未知函數f，則函數上的一點可以表示為式(1)。

f(x,y)=f(x0)=w(f(x1)-f(x0))

(1)

其中w的比率為式(2)。

(2)

按照自定義精度在矩形范圍內進行線性插值，精度越高，計算時間越長，然后將每個點與三角形進行判斷，判斷點是否在三角形內部。

獲取到所有在三角形內部的點后，使用Cesium提供Sample Terrain Most Detailed方法就能獲取每個內部的點的最大細化程度的高程值，。然后使用哈希表來存儲每個點高程信息。

2.4 點集的三角剖分

將任意多邊形區域切割成互相獨立的三角形，然后再對每個三角形的內部進行插值，由此每一個三角形對應了插值后一個點的集合。每一個集合要做一個三角格網化，筆者使用Delaunay三角剖分算法對點集合進行三角格網創建。

實現Delaunay三角格網有Lawson算法和Bowyer-Watson算法等。Lawson算法是由Lawson在1977年提出，該算法具有思路簡單明了、編程簡單并且容易實現的優點，同時被稱為逐點插入法[8]。Lawson的基本原理為首先創建一個包含散點集合中所有散點的簡單多邊形，將散點集合中未插入的散點逐一插入到三角格網中，并對新插入的點做空外接圓檢測和局部調整，要求重新生成的三角格網均符合Delaunay準則，最后移除包含初始化的多邊形頂點的三角形。

筆者使用改進的Lawson算法Bowyer-Watson算法實現地形三角格網剖分。Bowyer-Watson算法描述如下：

1)創建一個包含所有散點多邊形或者三角形，放入鏈表中。

2)按順序將集合中的散點插入到第一步創建的多邊形或者三角形中，在鏈表中找出外接圓包含插入散點的三角形，刪除外接圓的公共邊，形成Delaunay空腔。

3)插入的散點連接Delaunay空腔上的頂點，形成新的三角格網。

4)重復步驟2)、步驟3)，直到所有散點插入完畢。

2.5 區域面積求和

根據前面步驟能獲取到每個插值點的高度的信息，可以利用海倫公式(3)對三角格網中的每個三角形進行面積的計算。

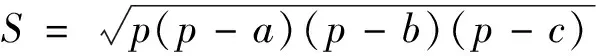
(3)

其中：a、b、c分別代表三角形三個邊的長度；p代表的是三角形的周長。每一個邊的邊長可以使用歐式距離公式來計算，n維歐式距離表示為式(4)。

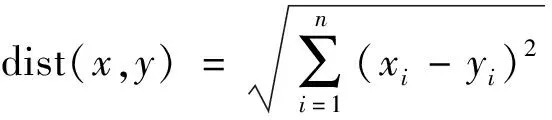
(4)

其中：n表示維度；x、y為在同一維度上的值。最后將三角格網中三角形的面積逐一相加，得到三維地形表面積測量的結果。

3 實例分析

筆者以Cesium.js作為3D WebGIS前端框架，IIS服務器為地形服務提供數據響應，用CesiumLab處理30 m分辨率的DEM數據產生.terrain格式的地形切片數據，以GeoServer為影像地圖服務器，本文所有的計算均是由瀏覽器內核計算，無后臺服務器提供計算。實驗環境是采用的win10操作系統，Cpu為i5-3470，瀏覽器是谷歌瀏覽器。

Cesium是由JavaScript腳本語言編寫的前端輕量級開源WebGIS框架，也是開源三維地圖引擎。Cesium不需要其他任何瀏覽器插件支持，只需要瀏覽器支持WebGL功能即可，并且具有跨平臺、跨瀏覽器的優點[9]。GeoServer是開源地圖服務器，能方便用戶快速的發布地圖影像數據。IIS是由微軟公司開發的Web服務程序。

在筆者研發的三維平臺上，分別選取地勢較為平坦、地勢較為陡峭、大面積區域、小面積區域、凸多邊形陡峭區域、凹多邊形陡峭區域、凸多邊形平坦區域、凹多邊形平坦區域共計8組相同控制點區域，利用傳統的投影方式與本文提出的三維地形面積測量方法來進行實驗，以15 m為插值點之間的間距來計算貼地面積。最終實驗對比結果見表1。

表1 面積測量結果對比分析

實驗在地勢陡峭區域的投影面積效果圖如圖3所示，貼地表面積如圖4所示，投影面積為4 805 292.3 m2，貼地表面積為5 696 831.239 m2。

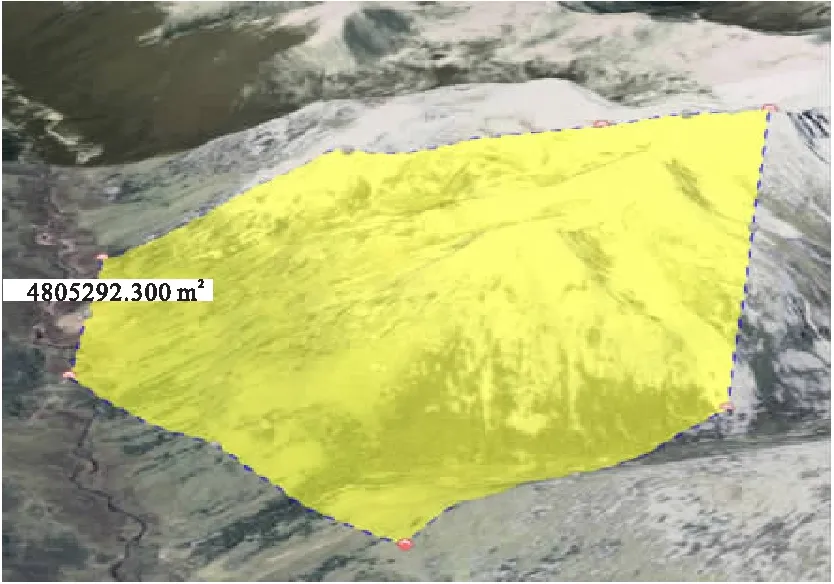
圖3 投影面積

圖4 貼地面積

由表1可知，在選擇同樣的控制點的情況下，投影面積始終小于貼地表面積，符合實驗的預期結果。在地勢較為平坦的情況下，投影面積和貼地表面積相差不是很大，在地勢較為陡峭的區域，投影面積和貼地表面積相差較大，這兩者從側面驗證了本文提出方法的可靠性。

4 結論

筆者提出了一種基于Web的三維地形表面積測量方法，其具有無需后臺服務器計算，依靠瀏覽器內核計算，同時能夠快速嵌入前端的特點。該方法在Cesium庫的基礎上結合耳切法、Delaunay三角網算法與線性插值構建區域三角網，然后利用海倫公式來求取三維地形表面積。其中耳切法、Delaunay三角網算法具有比較成熟且應用較廣的特點，能有效解決三維三角形格網面積的計算。該方法可以輔助人們在地勢陡峭難以測量的區域進行測量，例如滑坡面積測量以及露頭巖層面積的測量，一定程度上減少了人們到高危險區域的危險性以及費時、費力的局限性，同時也具有高度靈活測量的優點。