運用牛頓第二定律解決連接體問題
■貴州省天柱民族中學 胡朝平
多個相互關聯的物體由輕繩、輕桿、輕彈簧等連接在一起,或者疊放在一起,構成的物體系統稱為連接體。根據關聯物體速度的關系和連接物體介質的不同特點,靈活選用整體法和隔離法,利用牛頓第二定律可以順利求解相關問題。下面舉例分析。
一、根據關聯物體速度的關系可以分為同速連接體和關聯速度連接體
1.同速連接體:相互關聯的物體在拉力、彈力或摩擦力的作用下,具有相同的速度或相同的加速度。具體案例如圖1所示。
2.關聯速度連接體:相互關聯的物體的速度和加速度大小相等,方向不同,但有所關聯。具體案例如圖2所示。
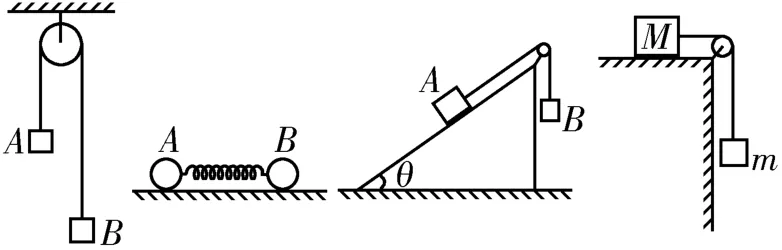
圖2
二、根據連接物體介質的不同可以分為輕繩連接體、輕桿連接體、輕彈簧連接體或疊放連接體
1.輕繩連接體。
輕繩連接體的特點:輕繩中張力的方向只能沿著輕繩并指向輕繩收縮的方向,輕繩只能提供拉力,輕繩的張力可以發生突變;輕繩平動時,兩端物體沿輕繩方向的速度(分速度)總相等;跨過滑輪、光滑桿、光滑釘子連接兩端物體的若是同一根輕繩,則輕繩對兩端物體的拉力大小相等。
例1質量不等的兩個木塊A、B,用跨過一輕質定滑輪的輕繩相連,在如圖3所示的情況下,木塊A、B一起做勻速運動。已知木塊A、B與桌面之間的動摩擦因數均為μ,且μ<1,重力加速度為g,空氣阻力、滑輪摩擦均不計。若木塊A、B的位置互相交換,則木塊A的加速度為( )。
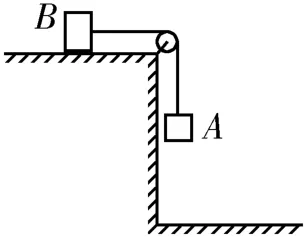
圖3
A.(1-μ)g
B.(1-μ2)g
D.與木塊A、B的質量有關
解析:木塊A、B一起做勻速運動的過程中,根據牛頓第二定律得mAg=μmBg。木塊A、B的位置互相交換后,同理得mBgμmAg=(mA+mB)a,解得a=(1-μ)g。
答案:A
2.輕桿連接體。
輕桿連接體的特點:輕桿對物體彈力的方向不一定沿著輕桿,輕桿既能提供壓力,又能提供拉力,輕桿的彈力可以發生突變。若將輕桿固定在墻壁上,則輕桿不能轉動。若用鉸鏈將輕桿與墻壁相連,則輕桿的受力方向一定沿著輕桿的方向。輕桿平動時,連接體具有相同的平動速度;輕桿轉動時,連接體具有相同的角速度,而線速度與轉動半徑成正比。一般情況下,連接體沿輕桿方向的分速度相等。
例2如圖4所示,傾角θ=30°的斜面體固定在地面上,光滑斜面上放一輛小車。一根彈性桿的一端固定在小車上,另一端固定一個質量m=0.2 kg的小球,取重力加速度g=10 m/s2。求:
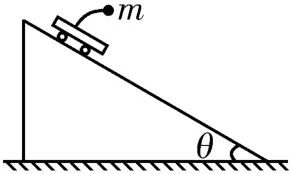
圖4
(1)當在外力作用下小車靜止在斜面上時,桿對小球的彈力。
(2)當小車由靜止沿斜面下滑時,桿對小球的彈力。
解析:(1)當小車處于靜止狀態時,小球處于平衡狀態,則桿對小球的彈力F=mg=2 N,方向豎直向上。
(2)當小球由靜止沿斜面下滑時,由小車、桿和小球組成的整體的加速度a=,小球受到的合外力F合=ma=1 N,方向沿斜面向下。根據平行四邊形定則可知,桿對小球的彈力F'=,方向垂直于斜面向上。
3.輕彈簧連接體。
輕彈簧連接體的特點:彈簧可以產生和承受沿彈簧伸縮方向的拉力和壓力。在彈簧發生形變的過程中,兩端物體的速率不一定相等;在彈簧形變量最大時,兩端物體的速率相等,兩端物體受到彈簧的作用力大小相等。
例3如圖5所示,置于粗糙水平面上的物塊A和B用輕質彈簧連接,在水平恒力F的作用下,A、B兩物塊以相同的加速度向右運動。A、B兩物塊的質量關系為mA>mB,兩物塊與水平面之間的動摩擦因數相同。為使彈簧穩定時的伸長量增大,下列操作可行的是( )。

圖5
A.僅減小物塊B的質量mB
B.僅增大物塊A的質量mA
C.僅將物塊A、B的位置對調
D.僅減小水平面的粗糙程度
解析:設彈簧的彈力為T,對由A、B兩物塊組成的整體應用牛頓第二定律得Fμ(mA+mB)g=(mA+mB)a,對物塊B應用牛頓第二定律得T-μmBg=mBa,解得T=僅減小物塊B的質量mB時,T減小,則彈簧穩定時的伸長量減小,選項A 錯誤;僅增大物塊A的質量mA時,T減小,則彈簧穩定時的伸長量減小,選項B 錯誤;僅將物塊A、B的位置對調,同理得彈簧的彈力,因mA>mB,故T'>T,則彈簧穩定時的伸長量增大,選項C 正確;因為T與μ無關,所以僅減小水平面的粗糙程度,彈簧穩定時的伸長量不變,選項D錯誤。
答案:C
4.疊放連接體。
疊放連接體的特點:疊放在一起的物體之間由于相對運動或相對運動趨勢會產生相互作用力;疊放在一起的物體之間相對靜止時具有相同的速度和加速度;疊放在一起的物體之間相對運動時具有不相同的速度和不相同的加速度。
例4如圖6所示,長木板放置在水平面上,一小物塊置于長木板的中央,長木板和物塊的質量均為m,物塊與長木板之間的動摩擦因數為μ,長木板與水平面之間的動摩擦因數為,假設最大靜摩擦力與滑動摩擦力大小相等,重力加速度為g。現對物塊施加一水平向右的拉力F,則長木板加速度a的大小可能是( )。
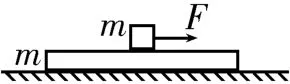
圖6
解析:水平面對長木板的最大靜摩擦力,若拉力F≤fmax,則a=0,選項A 正確。若物塊相對長木板運動,則μmg-·2mg=ma,解得此時的加速度為最大值,選項B 錯誤,C 正確。若長木板相對物塊靜止,長木板和物塊一起做勻加速直線運動,則由物塊和長木板組成的整體在水平方向上受到的力為Ffmax=2ma,解得,選項D 正確。
答案:ACD
處理連接體問題的方法:(1)若是同速連接體問題,則先用整體法求出F合與a的關系;若連接體內各物體具有相同的加速度,且不需要求物體之間的作用力,則可以把它們看成一個整體,分析整體受到的合力,應用牛頓第二定律求出加速度(或其他未知量),用隔離法求出F內與a的關系。(2)若是關聯速度連接體問題,則先將兩物體隔離開進行分析;若連接體內各物體的加速度不相同,或者需要求出連接體內各物體之間的作用力時,就需要用隔離法,應用牛頓第二定律列式求解。(3)整體法、隔離法往往需要交替運用。若連接體內各物體具有相同的加速度,且需要求出連接體內各物體之間的作用力時,可以先用整體法求出加速度,再選取合適的研究對象用隔離法,應用牛頓第二定律求作用力,即“先整體求加速度,再隔離求內力”。若已知連接體內物體之間的作用力,求連接體整體受到的外力,則“先隔離求加速度,再整體求外力”。
應用整體法和隔離法解題的技巧:(1)求解一起加速運動的物體系統問題時,若外力F作用在m1上,則m1和m2之間的相互作用力此結論與有無摩擦無關(若有摩擦,則兩物體與接觸面之間的動摩擦因數必須相同),物體系統沿水平面、斜面、豎直方向運動時,此結論都成立。兩物體之間的連接物為輕彈簧、輕桿時,此結論也成立。(2)求解通過跨過滑輪的輕繩連接的物體系統問題時,若需要求出輕繩的拉力,則往往需要采用隔離法,因為通過跨過滑輪的輕繩連接的兩物體的加速度雖然大小相同但方向不同。(3)求解疊加體系統臨界問題可以按照如圖7所示的程序進行。

圖7

1.如圖8所示,質量為m2的物塊B放在光滑的水平桌面上,其上疊放質量為m1的物塊A,用跨過光滑定滑輪的細線將物塊A與質量為M的物塊C相連,釋放物塊C,物塊A和B一起以加速度大小a由靜止開始運動。已知A、B兩物塊之間的動摩擦因數為μ,重力加速度大小為g,則細線中的彈力大小為( )。

圖8
A.Mg
B.M(g+a)
C.(m1+m2)a
D.m1a+μm1g
2.如圖9甲所示,在粗糙的水平面上,質量分別為m和M的物塊A、B用輕彈簧相連,兩物塊與水平面之間的動摩擦因數均為μ,當水平力F作用在物塊B上,且兩物塊一起向右以加速度a1做勻加速運動時,彈簧的伸長量為x1;如圖9乙所示,當將同樣大小的恒力F沿著傾角為θ的光滑斜面方向作用在物塊B上,且兩物塊一起以加速度a2沿斜面向上做勻加速運動時,彈簧的伸長量為x2。下列說法中正確的是( )。
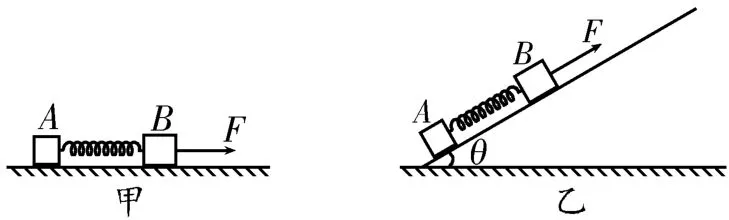
圖9
A.若m>M,則x1=x2
B.若m<M,則x1=x2
C.若μ>sinθ,則x1>x2
D.若μ<sinθ,則x1<x2
3.如圖10所示,水平地面上有三個靠在一起的物塊A、B和C,它們的質量均為m,設它們與地面之間的動摩擦因數均為μ,用水平向右的恒力F推物塊A,使三個物塊一起向右做勻加速直線運動,用F1、F2分別表示物塊A與B、B與C之間相互作用力的大小,則下列判斷正確的是( )。
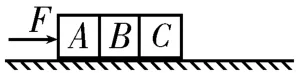
圖10
A.若μ≠0,則F1∶F2=2∶1
B.若μ≠0,則F1∶F2=3∶1
C.若μ=0,則F1∶F2=2∶1
D.若μ=0,則F1∶F2=3∶1
4.如圖11所示,置于水平面上的小車固定有一折成一定角度的細桿,細桿另一端固定了一個質量為m的小球,當小車以加速度a=g向左加速前進時,細桿對小球的作用力多大?方向如何?

圖11
參考答案:1.C 2.AB 3.AC
4.細桿對小球的作用力大小為2mg,其方向與豎直方向之間的夾角為45°。

