2021年全國高中數學聯賽一道解三角形試題的多解及推廣

葉誠理

(福建省福清第一中學 350300)

何 燈

(福建省福清第三中學 350315)

1 試題分析

2021全國高中數學聯賽一試A卷第5題：在△

ABC

中，則△

ABC

的面積為

.本題為解三角形問題，是競賽中常考的題型，難度與高考相當.題目已知三角形的兩邊和兩邊所對角之差，求面積的值，事實上得到的是一個固定的三角形，條件簡單直觀，屬于常規題型.從結果看，△

ABC

面積所以難點是如何運用條件結合正弦或余弦定理、三角形內角和公式，得出與

A

相關的三角函數值，需要考生從方程的角度進行運算、消元、轉化，或從圖形的角度進行分解、挖掘隱含條件，構建角或邊的等量關系.本題入口寬，解法多樣，是一道值得欣賞和研究的好題.本文從各種角度進行了一題多解，并對這一類題型的結論作了一般性推廣，與讀者共享.

2 試題解析

解法1

(公式法1)由正弦定理知又故2sin

C

=sin

C

，即

C

，故tan從而cos又故

評注

本解法通過正弦定理把邊

b

,

c

的關系轉化成角度

B

,

C

的關系，結合三角形內角和關系，運用三角恒等變換公式，轉化成與角

C

相關的三角函數計算問題.

解法2

(公式法2)由得由正弦定理知又因為得故

評注

本解法仍然是通過正弦定理把邊的關系轉化成角的關系，與解法1不同之處在于通過聯立角

A

,

B

,

C

的關系，把角

B

,

C

統一用角

A

表示，從而得到關于角

A

的三角關系式，體現了方程思想在解三角形中的應用.

解法3

(相似法)如圖1，在邊

AC

上取一點

D

，滿足則由得∠

DBA

=

C

，故△

ABD

∽△

ACB

，則有得所以在△

DBC

中，由余弦定理得得因此，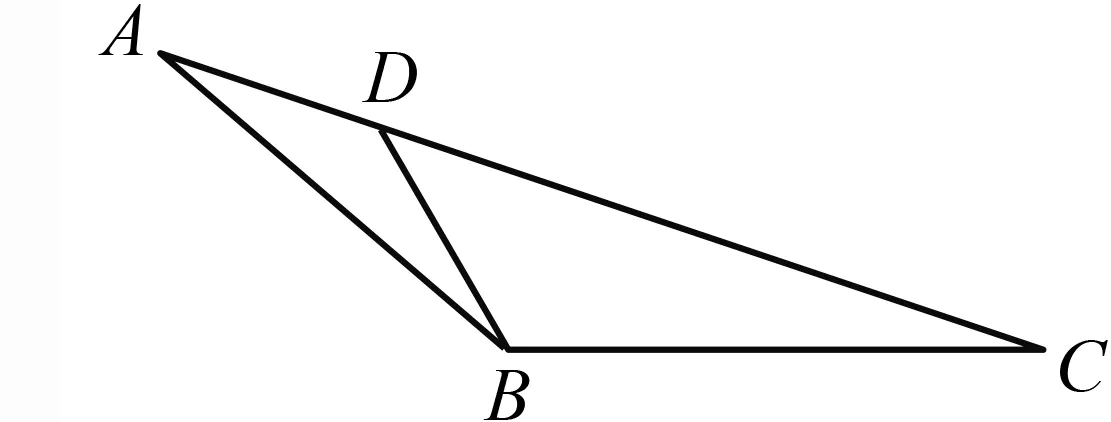

圖1

評注

本解法通過添加輔助線將角

B

分解為兩個角，從而構造兩個相似三角形，再利用余弦定理構建邊

a

的方程，實現了面積的轉化計算.

解法4

(坐標法)如圖2，以

B

為原點、

BC

為

x

軸建立平面直角坐標系，由

AB

=1，

BC

=

a

，設

A

(cos

B

,sin

B

)，又由

AC

=2，得(cos

B

-

a

)+sin

B

=4，有

B

=4，得sin故

S

=sin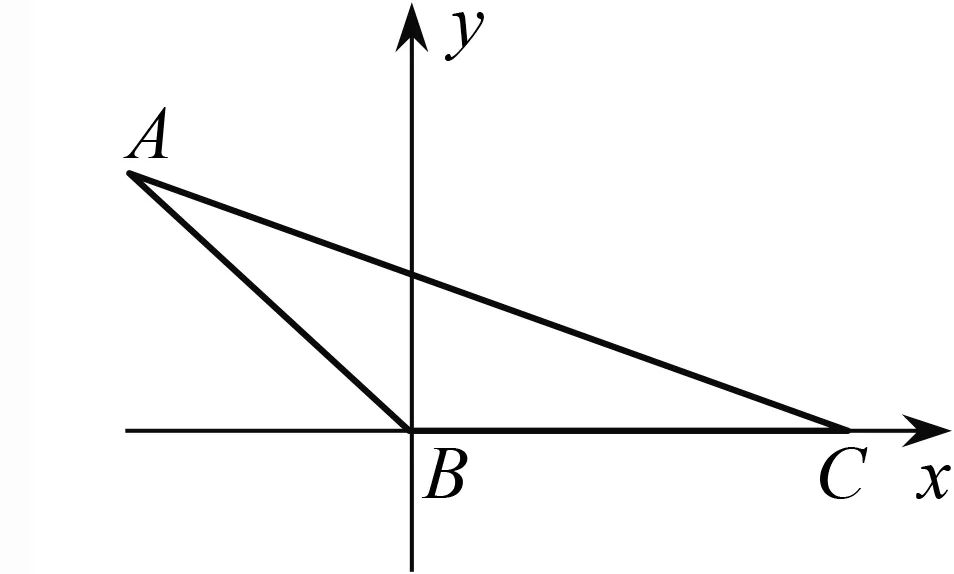

圖2

評注

本解法通過建立坐標系實現把解三角形問題運用解析幾何知識來求解.關鍵是幾何條件代數化，其中，以

B

為原點的好處是可以根據

AB

=1把點

A

看成是單位圓上的點，用角

B

巧設點

A

坐標.利用直線

AC

的斜率表達式，把含邊長

a

的關系式轉化成角

B

的三角函數，進而通過

AC

距離公式計算sin

B

，最終轉化成面積.

3 試題推廣

借鑒解法2，我們可以得到本題在一般情況下的結論.

推廣

在△

ABC

中，

AB

=

c

，

AC

=

b

，其中

b

>

c

且

B

-

C

=

α

>0，則△

ABC

的面積為

證明

考慮?

由正弦定理知又因為得即所以得即那么

4 解題心得

條條大道通羅馬，本題解法的多樣性讓我們感受到數學思維的無限魅力.解題中用到的知識涉及函數、方程、三角函數、平面幾何、解析幾何等；對一般性結論的推廣開闊了我們的視野，揭示了問題的本質.本題集中考查了解三角形問題中考生的抽象概括能力、運算求解能力和創新應用意識；用到的數學思想有函數與方程思想(特別是消元思想)、化歸與轉化思想、數形結合思想等.本題的一題多解彰顯出靈活合理地運用所學知識解決實際問題的能力的重要性，不僅對競賽生，也對廣大高考生具有一定啟發意義，即對數學知識的融會貫通、對數學方法的嫻熟運用和對數學思想的深刻領會是考場上制勝的關鍵.