數(shù)學(xué)運(yùn)算核心素養(yǎng)視角下的“三角函數(shù)”試題分析
許雅楠 黃在堂 孫艷雷 陳美賢

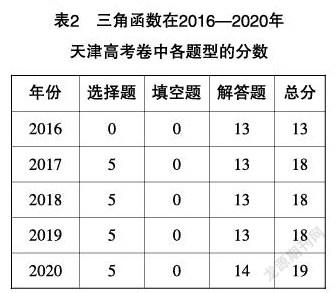
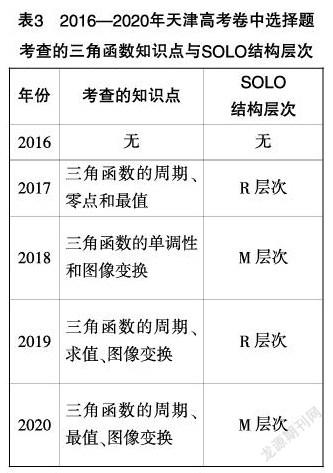

[摘 ?要] 數(shù)學(xué)運(yùn)算素養(yǎng)是影響學(xué)生高中數(shù)學(xué)學(xué)習(xí)的一個重要因素,所以選擇恰當(dāng)?shù)姆椒▽W(xué)生現(xiàn)階段數(shù)學(xué)運(yùn)算素養(yǎng)落實(shí)情況進(jìn)行考查是很有必要的. 在此基礎(chǔ)上,以SOLO分類理論為指導(dǎo),根據(jù)2016—2020年五年天津高考理科數(shù)學(xué)試卷所考查的“三角函數(shù)”知識點(diǎn)對數(shù)學(xué)運(yùn)算素養(yǎng)水平進(jìn)行劃分,得到這五年天津高考對學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)水平的要求,并由此給出提高學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)的一些教學(xué)建議.
[關(guān)鍵詞] 數(shù)學(xué)運(yùn)算;三角函數(shù);試題分析;SOLO分類理論
《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》中提出了高中數(shù)學(xué)六大核心素養(yǎng),分別是數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運(yùn)算和數(shù)據(jù)分析,并強(qiáng)調(diào)學(xué)科核心素養(yǎng)是育人價值的集中體現(xiàn),是學(xué)生通過高中數(shù)學(xué)學(xué)習(xí)而逐步形成的正確價值觀、必備品格和關(guān)鍵能力[1]. 其中數(shù)學(xué)運(yùn)算能力的提高不但可以幫助學(xué)生提升數(shù)學(xué)學(xué)習(xí)的邏輯思維能力和空間想象能力,還是提高學(xué)生數(shù)學(xué)建模能力的有效途徑,所以對學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)落實(shí)情況的考查是很有必要的. 考查學(xué)生核心素養(yǎng)落實(shí)情況最有效的途徑就是高考. 三角函數(shù)作為高考的必考內(nèi)容,它是高中學(xué)習(xí)的一類重要的函數(shù),涉及內(nèi)容偏多,形式抽象,需要學(xué)生具有較強(qiáng)的抽象能力和概括能力. 同時,三角函數(shù)的學(xué)習(xí)內(nèi)容與之前函數(shù)的學(xué)習(xí)內(nèi)容共同形成了龐大的函數(shù)知識體系,所以三角函數(shù)一直在高考中占有重……

