未知載荷條件下機械系統剩余壽命預測方法

許丹，肖小琦，馮至昕

（北京航空航天大學 可靠性與系統工程學院，北京 100083）

傳感器技術的發展為復雜的工程系統的狀態檢測與運行環境檢測提供了條件。其中，許多退化部件的傳感器信號被用于退化建模以預測退化部件的剩余壽命。對于設備退化建模與壽命預測，現有研究大多集中在單個傳感器信號在單個運行條件下的分析。具體來說，通常先根據歷史監測數據建立隨機退化模型，再根據現場傳感器實時采集到的監測數據對模型參數進行更新。周紹華等［1］使用非參數方法建立了稀疏數據單傳感器信號退化模型，其中工作狀態參數由極大似然估計（maximum likelihood estimate，MLE）算法獲取。在基于多傳感器信息退化建模方面［2-3］，通常先構建健康因子再進行退化過程建模。任子強等［4］將多個傳感器數據融合成一個復合健康指標，并采用線性維納過程對復合健康指標進行退化建模，進而得到系統的預測壽命。近年來，學者們開始研究基于機器學習的融合方法。馬奇友等［5］利用深度學習和長短期記憶組合來構造DLSTM網絡，將多個傳感器信號數據進行融合處理，得到系統剩余壽命預測。Chen等［6］提出了一種基于編碼器-解碼器框架的遞歸神經網絡，融合多個傳感器信號數據并預測HI值，通過線性回歸獲得最終的RUL值。但是，以上研究大多是考慮系統在單一工況下工作或者假設系統未來載荷與歷史載荷服從獨立同分布。目前，基于多傳感器信息變載荷退化建模的研究較少。Javed等［7］提出了一種基于小波極限學習機與減法最大熵模糊聚類的方法對多維變載荷條件下的退化數據進行降維，并利用降維后的特征來描述退化過程。Yan等［8］以最小化退化模型不確定度、最小化失效閾值不確定度及最大化信息范圍為目標進行線性優化，得到考慮變載荷情況下的傳感器數據加權系數，構建健康因子。而在變載荷退化建模與預測中，未來載荷的不確定性也是研究的一個難點。Flory等［9］假設變載荷狀態為一個馬爾可夫過程，通過蒙特卡羅抽樣與經典貝葉斯信息準則的方法從傳感器信息中估計環境狀態參數，作為變換融合模型的輸入，估計退化過程的首穿時分布。

在許多情況下，系統通常會在多個載荷下工作，且載荷變化的下一個狀態常常與此前的工作狀態無關，即可以假設為具有馬爾可夫的無后效特性。而隱藏的半馬爾可夫鏈具有用于近似復雜概率分布的隱馬爾可夫鏈的靈活性和用于表示時間的半馬爾可夫鏈的靈活性，常用于設備的故障診斷及預測［10-11］。因此，本文提出一種基于隱半馬爾可夫模型（hidden semi-Markov model，HSMM）的隨機載荷空間構建和預測的方法。首先，采用HSMM對隨機載荷空間進行建模。然后，結合多傳感器信息的剩余壽命預測方法，得到針對未來載荷未知條件下的基于多傳感器信息的變載荷下剩余壽命預測方法。

1 隨機載荷建模

1.1 隱半馬爾可夫模型

在常規的馬爾可夫模型（Markov model，MM）中，模型在某狀態停留一定時間的概率為非顯式的概率模型，也就是說，沒有參數化的表達形式。HSMM通過在隱馬爾可夫（hidden Markov model，HMM）中添加顯式時間組件（temporal component）來改進HMM模型中不準確的時間建模。研究人員提出，用精心選擇的概率函數替換持續時間概率函數［12］，而具有這種精心選擇的狀態時間概率函數的HMM模型成為HSMM模型。

HMM過 程 由π、A、B等 元 素 構 成［13］。與HMM模型不同，HSMM模型會在一個狀態中產生一系列的觀測值，HSMM模型參數可以記為

式中：π為初始狀態分布；A為狀態轉移模型；B為觀測概率模型；St表示t時刻下的隱藏狀態；O為觀測序列；D為狀態停留時間分布。

1.2 基于HSMM的隨機載荷空間建模

系統在工作中，常常需要經歷多個工作狀態，如發動機在不同的馬赫數、油門解算器角度、飛行高度時，會對應不同的工作狀態，即變載荷狀態空間。在載荷隨機變化的過程中，可以將其視為具有N個不同序貫狀態的過程。令di表示載荷i下的停留時間，T表示該系統歷經所有載荷的總時長，則有

假設HSMM模型中的狀態序列χ包含了N個部分，令qi為一個部分中結束的時間點，則該狀態序列可以表示為表1。載荷空間變化過程如圖1所示。

表1 HSMM模型特征量Table 1 Characteristic variables in HSMM

圖1 HSMM載荷空間變化示意圖Fig.1 Sketch map of load space change of HSMM

為實現上述基于HSMM模型的隨機變載荷空間模型，對變載荷空間進行預測，采用改進的前向-后向變量與Viterbi算法，并通過動態規劃方法對模型進行求解。

首先，將時間t時狀態i下觀測狀態o1，o2，…，ot的聯合概率分布定義為αt（i），即前向變量。同樣，可以推出后向變量βt（i）。前-后向變量計算過程如圖2所示。對于HSMM模型λ：

圖2 前向-后向變量算法示意圖Fig.2 Sketch map of forward-backward variable algorithm

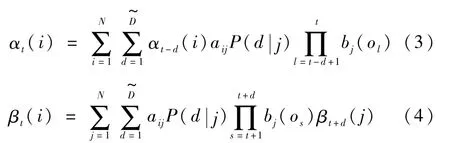
O在給定HSMM模型的情況下的概率模型可以記為

為對模型的其他參數進行求解，繼續定義了3個變量：第1個變量為載荷處于狀態i時停留時間di，再跳轉到狀態j的平均概率值?t，t′（i，j）；第2個變量為時刻t處于狀態i和時刻t′處于狀態j時的部分觀測值o1，o2，…，ot′的聯合概率αt，t′（i，j）；第3個 變 量 為 在 給 定 觀 測 值 序 列o1，o2，…，oT載荷處于狀態i時的停留時間為di=t′-t，再跳轉到狀態j的概率值ξt，t′（i，j）。

Viterbi算法的流程可以參考文獻［12］。令λ表示部分HSMM過程的參數集，則對于觀測序列O與對應的狀態序列Z可以寫為

式中：θdi與θfi為對應分布的參數集。

通過EM算法，可以對λ進行求解，其求解過程可以總結為如下過程。

M步驟：設定新的λnew使得對數極大似然函數最大：

2 未知載荷條件下的剩余壽命預測

2.1 基于HSMM的隨機載荷預測

1）初始狀態分布

在已知O時，模型的初始狀態即在狀態i為初始狀態的概率：

2）狀態轉移概率

狀態轉移概率的估計為從狀態i轉移到狀態j的期望與從狀態i轉移的總期望值之間的比值：

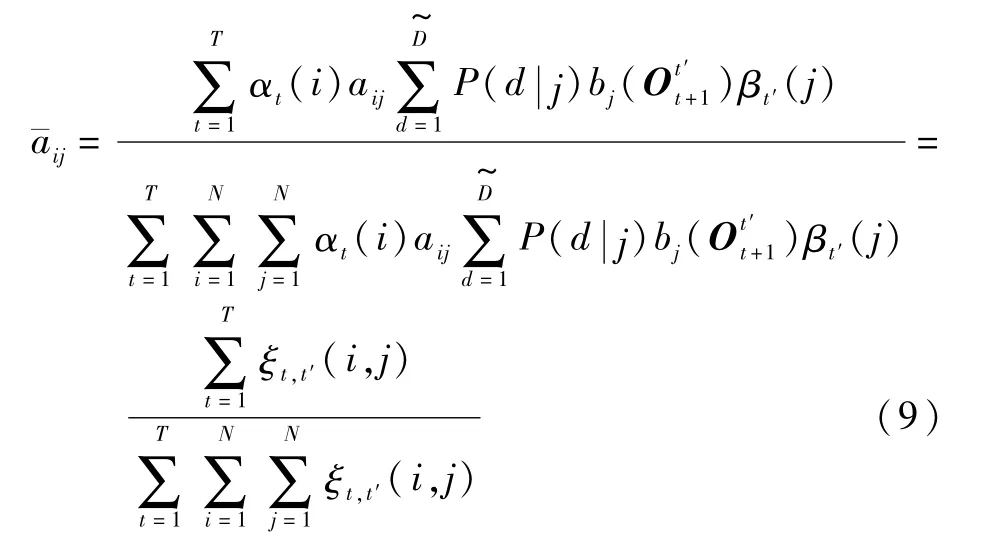
3）觀測值分布

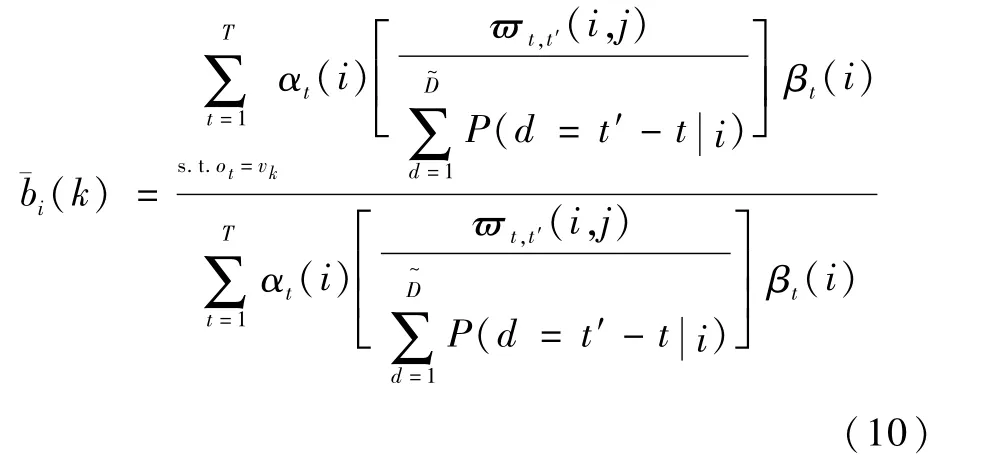
當使用顯式狀態停留時間模型時，狀態停留時間密度反映在觀測值中的重要性在于可以顯著提高模型的質量。然而，使用顯式狀態停留模型當作狀態停留時間密度有一定的缺點：①會使與狀態停留時間相關的變量計算量大增；②包含了除基本的HMM模型參數外的與每個狀態都相關的大量參數d的模型。因此，HSMM模型的參數估計過程比標準的HMM過程更加困難。解決問題的方案是使用參數化狀態停留時間密度函數而不是非參數密度函數。同時，綜合考慮高斯分布、威布爾分布等分布的應用情況和在訓練時計算量的大小，本文采用高斯分布對狀態停留時間概率進行建模。狀態停留時間參數通過訓練集進行估計，狀態停留時間的高斯分布的均值與方差可通過如下步驟進行估計。

1）訓練HSMM模型識別N個不同載荷，即建立對載荷進行分類的模型。已知N組觀測序列，對N組不同的HSMM模型（如HSMM1，HSMM2，…，HSMMN）中的每一組都進行特征建模。

2）對HSMM模型進行分類。在給定觀測序列時，N組HSMM模型中的每一個都通過同一序列呈現。根據極大似然估計，可以對這些序列進行分類。

式中：D（Zi）表示載荷Zi的狀態停留時間分布；μ（Zi）和σ2（Zi）分別為均值和方差；ρ為相應的系數。

具體的狀態停留時間模型預測步驟如下：

步驟1 通過HSMM訓練程序（如參數估計），從而可以獲取HSMM的狀態轉移概率。

步驟2 通過HSMM的參數估計，每一個載荷下的狀態停留時間的概率分布函數可以獲取。

步驟3 通過分類，可以識別實時的載荷。

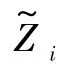
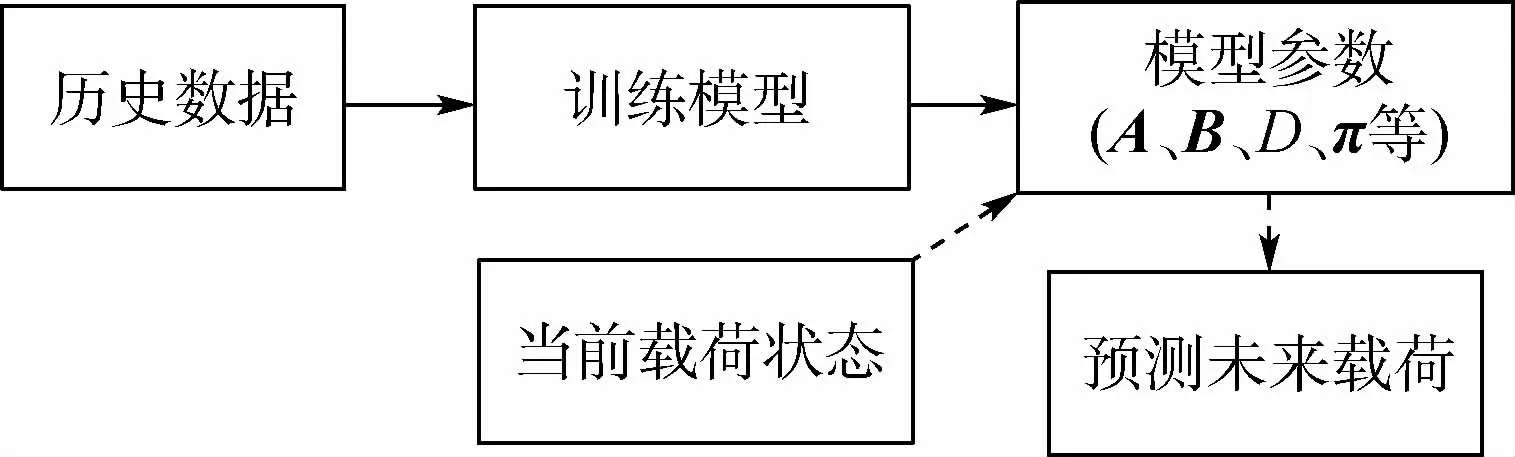
圖3 基于HSMM的隨機載荷預測Fig.3 Random load prediction based on HSMM

2.2 基于隨機預測載荷的剩余壽命預測

基于本文提出的隨機載荷預測方法，可以得到每一個HSMM模型中每一個狀態的停留時間分布D及狀態之間的轉移概率A。基于所求解的HSMM模型，已知tk-1時的狀態概率Zi，遞推在時間tk時狀態為Zj的概率為

基于這一遞推公式，可以得到每一時刻的載荷與處于該載荷的概率。將這些概率代入文獻［14］中所述的預測壽命的方法，便可計算得出預測的剩余壽命：

式中：yi為系統/部件的失效時間；Ω（·）為累積分布函數；σ為尺度參數；π（si，p，l（t））為位置參數；si，p，l（t）為載荷l下第i個系統第p個傳感器的退化信號。

系統剩余壽命為式（14）得到的壽命估計值減去實時的時間值。基于隨機預測載荷的剩余壽命預測流程如圖4所示。

圖4 基于隨機預測載荷的剩余壽命預測Fig.4 Remaining life prediction based on random load prediction

得到剩余壽命后，對其進行誤差分析來驗證本文方法的準確性。剩余壽命相對誤差計算方法如下：

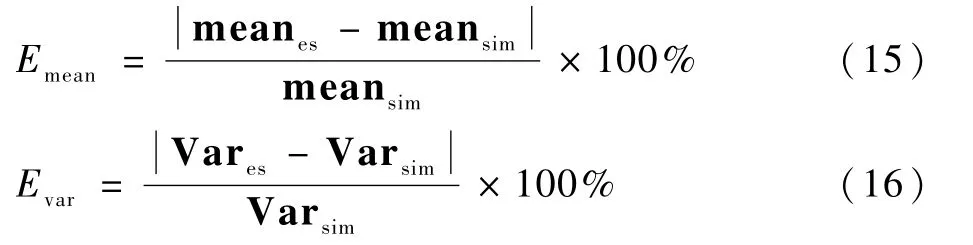
式中：Emean為均值的相對誤差；Evar為方差的相對誤差；meanes和meansim分別為預測得到的剩余壽命分布的均值和原始數據庫中的剩余壽命分布均值；Vares和Varsim分別為預測得到的剩余壽命分布的方差和原始數據庫中的剩余壽命分布的方差。

3 發動機應用案例

商用模塊化航空推進系統仿真（C-MAPSS）數據庫的多傳感器退化數據為基于物理退化模型的飛機渦扇發動機仿真數據［15］。本文選取CMAPSS數據庫中發動機在多種載荷條件下的性能退化數據進行應用案例驗證。圖5展示了CMAPSS系統中的發動機主要部件。所使用的數據基于如下假設：發動機退化是由于單個部件（如高壓腔與高壓壓氣機）在使用過程中特定載荷下的磨損引起的。同時，在數據庫中，特定飛機上的損傷累計是無法直接基于飛行時間與飛行載荷計算的。因此，只能使用飛行過程與飛行剛剛結束時多傳感器記錄的退化信號對飛機渦扇發動機的剩余壽命進行計算。

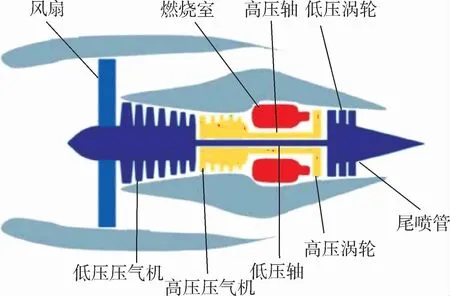
圖5 商用渦扇發動機結構簡圖Fig.5 Structure of commercial turbofan engine

該仿真數據庫包含260個樣本，挑選其中的80%（208個）作為歷史數據，剩余20%（52個）作為在線測試樣本。其中，包含了21個性能傳感器參數，同時包含了3個表征載荷狀態的傳感器。載荷狀態空間如表2所示，其不同載荷主要由3個指標表征，即馬赫數、高度、油門解算器角度（TRA）。從表2中可知，這3個表征載荷的指標綜合構成6個不同的載荷狀態，該仿真數據在這6種載荷狀態下仿真得來的。由于渦扇發動機整體結構十分復雜，難以建立準確的物理模型，采用基于數據的傳感器融合方法進行處理，并基于訓練集數據對測試集樣本進行未來載荷未知情況下的剩余壽命預測研究。

表2 載荷狀態空間Table 2 Space of load states

圖6展示了6個不同載荷條件隨時間變化的過程。可以看出，在渦扇發動機模擬仿真過程中，6個應力狀態隨時間變化，且綜合考慮數據庫中所有的數據，載荷變化呈現出一定的隨機性。也就是說，3個表征載荷狀態的參數呈現出隨時間變化的特點且具有一定的隨機性，同時，可以認為后續狀態只與前一個狀態相關而與之前的其他狀態無關，即具備馬爾可夫空間的無后效性。同時，表征3個指標的傳感器可以視為觀測狀態，而不同的觀測狀態的組合構成了載荷狀態，因此可以根據基于HSMM模型的剩余壽命預測方法對CMAPSS仿真數據中的隨機載荷進行建模，將這6個載荷空間中不同載荷狀態下的停留時間視為一個隨機分布過程，并使用高斯過程對狀態停留時間進行擬合。從而得到基于HSMM模型的載荷空間構建，通過2.1節中提出的模型參數方法對載荷空間的參數進行求解，從而在未來載荷未知的情況下對載荷變化進行預測，為未來載荷未知時的渦扇發動機剩余壽命預測提供基礎。

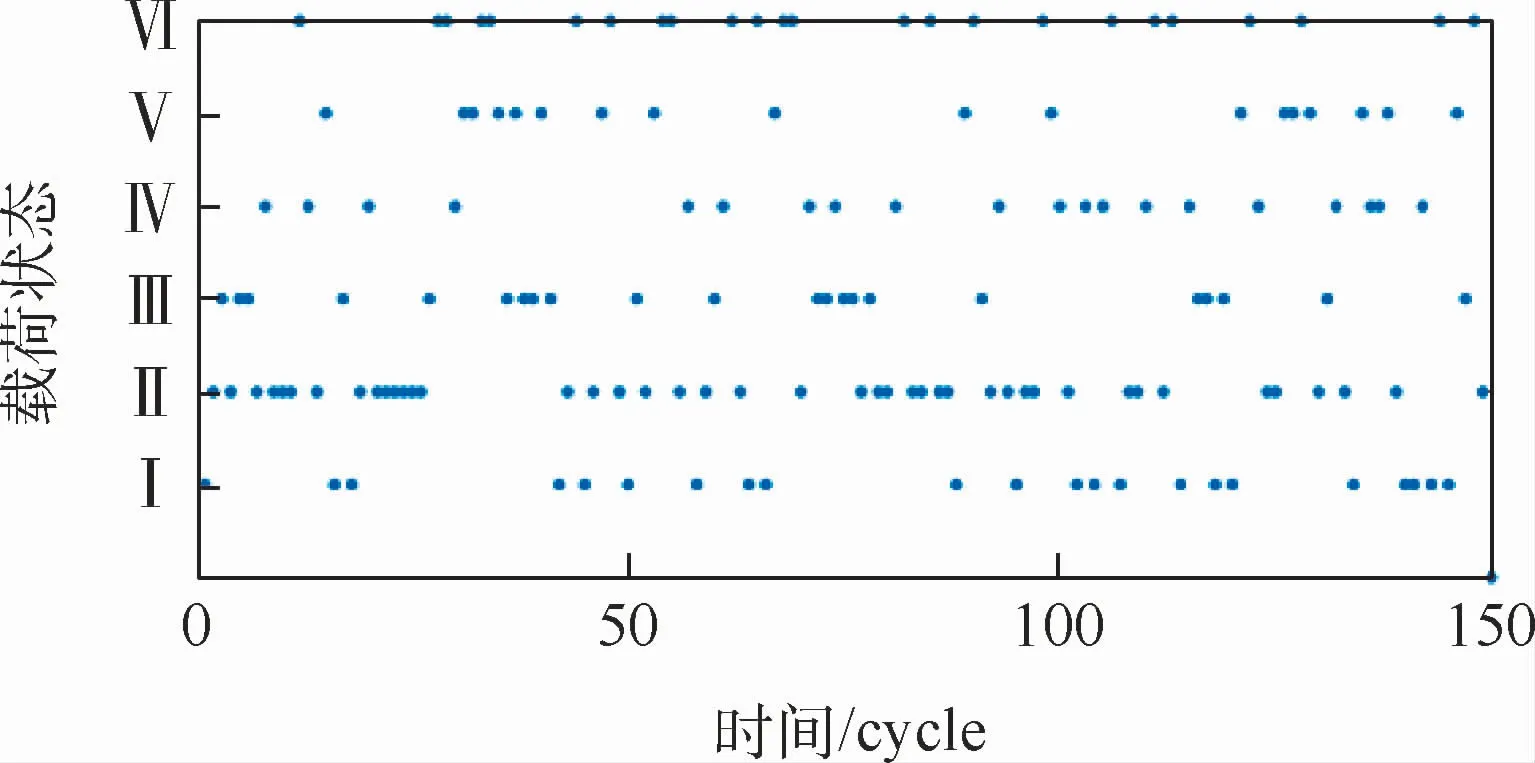
圖6 六個載荷狀態隨時間變化示意圖Fig.6 Sketch map of six load states changing with time

首先，基于2.1節提出的基于HSMM模型的變載荷空間建模與參數預測方法，可以求解得到HSMM模型的相應參數，如表3和表4所示。假設初始狀態為狀態Ⅴ，未來載荷預測結果如表5所示。基于這一載荷模型可以對未來載荷的變化情況進行預測，結合文獻［14］中提出的預測方法與式（13），可以對載荷未知的條件下的剩余壽命進行預測。基于HSMM模型的變載荷空間建模與參數預測方法是基于過去已知載荷預測未來載荷并代入壽命預測模型預測壽命，案例中同時也使用發動機從開始到失效真實經歷的載荷代入文獻［14］的方法進行壽命預測，即未來載荷已知的情況。

表3 六個載荷狀態之間的轉移概率矩陣Table 3 Transition probability matrix of six load states

表4 六個載荷狀態各自停留的時間均值與方差Table 4 Average and variance of settling time under six load states

表5 未知載荷預測結果Table 5 Pr edicted results for unknown loads

使用不同使用信息占比下的部分剩余壽命預測結果如表6與表7所示。為了分析預測結果的準確性，再根據式（15）和式（16）計算剩余壽命相對誤差的均值與方差值，如表8與表9所示。

表6 未來載荷已知時的剩余壽命Table 6 Remaining life when future loads are known

表7 未來載荷未知時的剩余壽命Table 7 Remaining life when future loads are unknown

表8 剩余壽命相對誤差均值Table 8 Average relative error of remaining life

表9 剩余壽命相對誤差方差Table 9 Variance of relative er ror of remaining life

從表8和表9可以看出，預測模型達到了一定的準確度，即對均值與方差的估計值與載荷已知條件下的誤差相差小于5%。因此，使用HSMM模型對隨機載荷空間進行建模與預測具有一定的有效性。通過表8和表9可以看出，在使用數據占比越大時，對剩余壽命的均值與方差估計值的估計誤差越小。這是由于大量的數據提高了模型參數估計值精度提高，從而提高整個模型的預測精度。

4 結 論

針對運行在多工況下的機械系統，本文提出的基于隱半馬爾可夫模型的壽命預測方法解決了未來載荷未知情況下的壽命預測問題。通過案例應用，驗證了本文提出的預測方法的有效性和正確性。

1）相比于當前壽命預測方法僅考慮單一工況或者系統未來載荷與歷史載荷服從獨立同分布的假設，本文將預測的未來載荷信息代入壽命預測模型進行壽命預測，更符合實際情況。

2）與發動機真實載荷代入計算的結果進行比較，結果表明本文提出的基于隨機預測載荷的剩余壽命預測方法具有一定的準確性。由于載荷預測模型引入了預測誤差，這種情況下的剩余壽命預測值比載荷已知時的剩余壽命預測值的相對誤差更大，但是依然保持在較低的水平。