基于調制卷積神經網絡的空地數據鏈信道估計

劉春輝，王美琳，董贊亮，王沛

（1.北京航空航天大學 無人系統研究院，北京 100083； 2.北京航空航天大學 電子信息工程學院，北京 100083）

空地數據鏈（air-ground data link）系統是無人機、無人飛艇等無人空中系統的重要組成部分，實現無人空中平臺的指揮控制和信息傳輸功能。當無人空中平臺在復雜地理環境中執行任務時，數據鏈系統常受到“多徑效應”的影響。為克服多徑效應，正交頻分復用（orthogonal frequency division multiplexing，OFDM）技術被廣泛應用于空地數據鏈系統設計［1］，OFDM系統通過在符號之間插入大于無線信道最大多徑時延擴展的循環前綴（cyclic prefix，CP），最大限度消除由多徑效應產生的符號間干擾［2］（inter symbol interference，ISI）。然而，對于一些高度散射信道，較大的多徑時延要求CP必須很長，但過長的CP會導致信息傳輸速率降低。針對這一問題，通常增加信道估計和信道均衡等模塊來減小CP的長度，即通過增加系統復雜性換取系統頻帶利用率的提高。信道估計用于實現無線信道參數的有效估計，包括信道階數、多普勒頻移和多徑時延等參數，這些參數均反映在信道沖激響應矩陣中，因此信道估計性能直接影響著空地OFDM數據鏈的整體接收性能。

傳統的信道估計算法可分為基于導頻的信道估計算法、盲估計和半盲估計，其中基于導頻的信道估計算法最為常見。經典的基于導頻的信道估計算法有最小二乘算法（least square，LS）［3］、最小均方誤差算法（minimum mean-square error，MMSE）［4］和線性最小均方誤差算法（linear minimum mean-square error，LMMSE）［5］等。LS算法計算簡單、復雜度低、不需要信道的任何先驗信息，因此在實際中被廣泛使用；MMSE算法需要信道的統計信息同時利用信道的相關性抑制噪聲，具有較好的信道估計性能，但計算復雜度較高；LMMSE算法對MMSE算法進行了改進，簡化了MMSE算法的計算，因此在實際應用中常用LMMSE算法代替MMSE算法。

近年來，深度學習開始應用于OFDM信道估計與信號檢測領域，顛覆了傳統信道估計算法需要在線訓練的要求。文獻［6］采用大數據訓練的方式將OFDM接收機視為一個“黑箱子”，利用標準的全連接神經網絡實現信道估計與信號檢測；文獻［7］設計了一種基于模型驅動的深度學習方法用于信號檢測；文獻［8］利用傳統通信理論分別設計了信道估計和信號檢測2個子網絡，不僅使每個子網絡都具有清晰的物理意義，還使子網絡不依賴于大量的樣本數，加快了訓練速度；文獻［9］提出了利用深度神經網絡（deep neural network，DNN）估計信道響應與信道的頻域相關系數，實時追蹤信道的頻域變化；文獻［10］基于卷積-長短時記憶-全連接深度神經網絡（convolutional，long short-term memory，fully connected deep neural networks，CLDNN）網絡結構［11］提出了在高速移動環境下的信道估計算法，采用一維卷積神經網絡（convolutional neural network，CNN）與雙向長短時記憶網絡（bidirectional long short-term memory，BiLSTM）結合的網絡結構進行信道估計，克服了多徑效應和多普勒效應的影響；文獻［12］提出了基于二維CNN與BiLSTM結合的用于多輸入多輸出正交頻分復用（multiple-input multiple-output orthogonal frequency division multiplexing，MIMO-OFDM）系統的信道估計算法，實現高速移動場景下的快速時變信道估計；文獻［13］設計了基于模型驅動的全連接神經網絡OFDM接收機，補償了多徑效應和非線性失真；文獻［14］設計了利用人工智能輔助的OFDM接收機，應用在無CP的OFDM系統中，提升了頻譜和能量利用率。

從當前研究現狀來看，深度學習方法在空地數據鏈信道估計領域尚未開展深入研究，這是由于復雜環境下空地信道的多徑效應產生機理比一般場景更復雜，信道樣本數據的多樣性要求更高，造成信道估計難度加大。與蜂窩移動通信或衛星通信系統相比，空地通信系統有其獨特的信道特性，因此對空地信道進行準確地建模對提升信道估計算法的估計精度至關重要。

在空地信道建模研究方面，文獻［15-17］綜合分析了空地信道特點，對不同地表環境下的空地信道進行建模，提出了在經典二徑空地信道模型［15］的基礎上加入間歇多徑分量（multipath component，MPC）形成抽頭延時線（tapped delay line，TDL）模型，實現對復雜環境多徑空地信道的建模。其中，文獻［15］重點介紹水上環境（包括海水和淡水）的空地信道建模方法；文獻［16］重點介紹山區環境的空地信道建模方法；文獻［17］重點介紹郊區環境的空地信道建模方法。

除了空地信道樣本建模困難，基于深度卷積神經網絡的空地信道估計模型在機載端的部署同樣存在難度。這是由于卷積網絡模型大規模的網絡權重對存儲器帶寬具有較高的要求，同時為了實現網絡中最常見的點積運算需要進行大量的計算，這些都會造成過高的功率開銷，為功率受限的機載應用帶來較大挑戰。針對機載部署問題，需要對神經網絡模型進行壓縮來獲得輕量化的模型。CNN模型輕量化的研究主要分為2個方向：一是模型結構簡化，通過設計輕量級的模型減少計算量和參數量；二是模型壓縮，減少現有模型的大小，使模型能夠部署應用于小型設備。具體研究工作可以分為3類：網絡剪枝［18］、模型量化［19］、低秩分解［20］。其中，模型量化基于權重共享思想使多個網絡連接的權重共用同一權值。調制濾波器（modulated filter）是模型量化的代表性技術，通過生成調制卷積神經網絡（modulated convolutional neural network，MCNN）對原始CNN網絡進行模型壓縮。

針對上述問題，本文提出一種基于MCNN和BiLSTM結合的OFDM信道估計算法，利用TDL模型對復雜環境多徑空地信道進行建模［15-17］，仿真生成具有模擬復雜空地環境多徑時延擴展特征的信道樣本數據，利用調制濾波器對CNN網絡參數進行壓縮，充分發揮MCNN［21］網絡對信道樣本特征的提取能力和BiLSTM網絡［22］對信道樣本序列的預測能力，實現多徑空地信道的準確估計。同時，本文還通過增減MCNN和BiLSTM的層數來分析網絡層數對信道估計精度的影響。與傳統的LS算法、LMMSE算法及現有的深度學習方法DNN相比，本文提出的信道估計算法有效提高了不同應用環境中空地數據鏈的信道估計精度。

1 OFDM通信系統

OFDM是一種高速無線傳輸技術，該技術的基本原理是將高速串行數據變換成多路相對低速的并行數據，進而實現多載波調制。圖1為OFDM通信系統的結構［9］。

如圖1所示，在通信系統的發射端，發射機發射二進制信號，信號經過調制后進行串并轉換將高速的串行比特流轉換成N條并行的低速數據流，映射到OFDM符號的不同子載波上進行傳輸。

在OFDM系統中，各子載波之間相互正交，且每一個子載波在一個OFDM符號周期內都包含整數倍周期，相鄰的子載波之間相差一個周期。其正交性可表示為

式中：ωi為第i個子載波的角速度。

為了消除符號間干擾和防止載波間的正交性被破壞，需要在OFDM符號間添加CP，CP的長度一般要大于無線信道的最大時延擴展，這樣一個符號的多徑分量就不會對下一個符號造成干擾。最終將多載波調制后的并行數據轉換成串行數據傳輸到多徑信道中。發送信號第n個OFDM符號sn（m）為

式中：K為子載波數；Xn，k為串并轉換后的并行傳輸信號；?k為第k個子載波的角速度。

在通信系統的接收端，將接收到的串行數據轉換成并行數據后去除CP，并通過快速傅里葉變換對OFDM符號實現解調。接收信號為

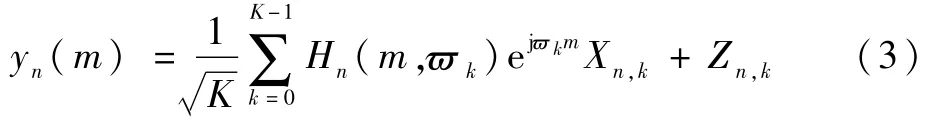
式中：Hn（m，?k）為多徑傳輸信道；Zn，k為加性高斯白噪聲。

為了在接收端更好地恢復發射信號，需要進行信道估計，再利用信道估計結果進行信道均衡，進而實現解調，恢復發送的信號。

2 空地信道建模

本節基于經典的二徑空地信道模型，利用包含直射分量、反射分量及間歇多徑分量的TDL模型對本文需要的空地信道進行建模。

2.1 二徑信道模型

2.1.1 模型參數

圖2為簡化的二徑空地信道模型，二徑信道模型由直射路徑分量和反射路徑分量組成［15］。圖2中：hA和hG分別為飛機和地面天線的高度；d為兩者地面距離；ψ為地面反射分量的掠射角。

圖2 二徑空地信道模型Fig.2 Two-ray air-ground channel model

在二徑信道模型中，地表反射是由地面平整度和地面站的半徑Q范圍內的植被覆蓋率決定的，即地面反射點應位于地面站的半徑Q內。通過相似三角形關系，存在如下等式：

二徑信道模型相關參數計算如下：

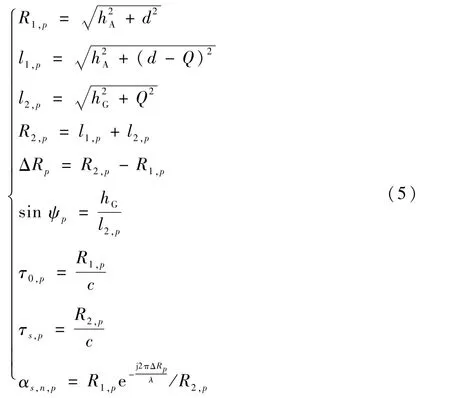
式中：R1，p為直射分量路徑長度；l1，p為反射分量第一段路徑長度；l2，p為反射分量第二段路徑長度；R2，p為反射分量路徑總長度；ΔRp為反射分量和直射分量路徑差；ψp為p時刻的掠角；τ0，p為直射分量路徑時延；τs，p為反射分量路徑時 延；αs，n，p為表面相對反射系數；c為光速；λ=c/fc為波長，fc為載波頻率。

依據文獻［15-17］，p時刻的二徑空地信道的沖激響應為

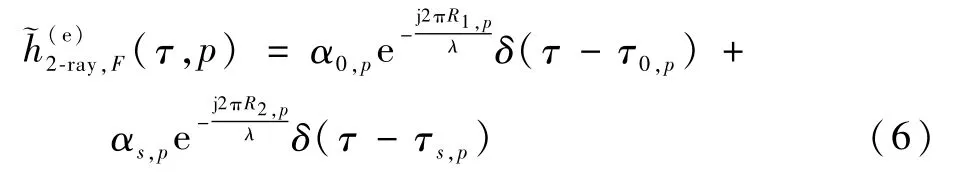
假設R1，p為 已 知，此 時α0，p和τ0，p也 為 已 知。對式（6）進行歸一化，使得LOS分量的振幅α0=1，延時τ0，p=0，則信道沖激響應（channel impulse response，CIR）可以重新表示為

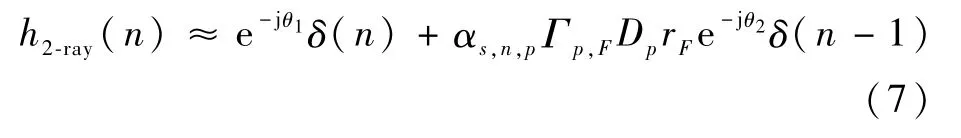
式中：θ為相位；Γp，F為表面反射系數；Dp為p時刻的散度因子；rF為表面粗糙因子。

此時，決定二徑空地信道CIR的3個參數為：表面粗糙因子rF、p時刻的散度因子Dp和表面反射系數Γp，F。

2.1.2 表面粗糙因子rF

理論上，如果地球表面絕對光滑，則rF=1，但實際情況一般rF＞1。

2.1.3 散度因子Dp

p時刻散度因子Dp的計算方法為

式中：k=4/3；α為地球赤道半徑。

2.1.4 表面反射系數Γp，F

Γp，F取決于頻率、極化、入射角和反射表面介電常數，本節采用簡化計算方法，根據文獻［23］，p時刻的表面反射系數的簡化計算方法為

式中：η1為介質1的相對介電常數；η2為介質2的相對介電常數。

2.2 帶有間歇多徑分量的TDL模型

文獻［16］提出空地信道TDL模型中最多有9個抽頭，因此本文采用的TDL模型的信道沖激響應表達式如下：

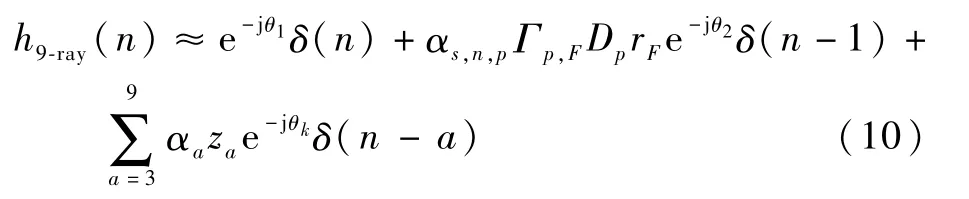
式中：α和θ分別為振幅和相位；z∈（0，1）用來描述抽頭開關的概率；下標a為第a次間歇多徑分量，a為3～9的整數。

3 基于深度學習的信道估計技術

針對復雜環境下空地OFDM信道估計難題，本文提出的基于深度學習的信道估計神經網絡框架如圖3所示，包括輸入層、隱藏層、輸出層及網絡訓練4部分。

圖3 基于深度學習的信道估計框架Fig.3 Channel estimation framework based on deep learning

3.1 網絡輸入層

首先，利用第2節提出的9徑TDL模型對空地信道進行建模，生成信道系數樣本數據集。然后，對數據集進行劃分，分為導頻序列和數據序列，利用LS算法處理導頻序列，估計得到導頻符號處的信道狀態信息（channel state information，CSI）［24］：

式中：HLS（q）為LS算法計算得到的第q個子載波處的CSI；xpilot（q）為第q個子載波的發送導頻信號；ypilot（q）為第q個子載波的接收導頻信號。

數據符號處的CSI初始化為0，則網絡輸入數據表達形式為

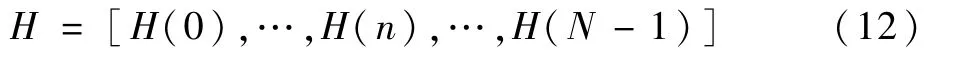
式中：H（n）為第n個OFDM符號處的CSI。

最后，由于信道數據為復數信號，對網絡進行輸入之前需要把輸入數據的實部和虛部提取出來結合成一個維度。

3.2 網絡隱藏層

CNN具備較強的局部數據特征提取能力，但其結構一般包含多個卷積層，每個卷積層中又蘊含著大量卷積核參數。為了去除CNN參數冗余，降低計算復雜度，本文將調制濾波器技術引入一維CNN，建立了一種生成CNN的新型網絡結構，即MCNN。

調制生成卷積核的優點在于：①調制濾波器能增強及引導隨機的原始卷積核屬性，使網絡更高效；②通過引入卷積核調制過程，可通過共享調制濾波器的方式減少深度神經網絡參數，使模型更緊致。基于MCNN結構，本文提出了一種基于MCNN與BiLSTM的信道估計網絡（以下簡稱MC-BI網絡）。

3.2.1 MCNN網絡單元結構

在利用調制方法生成卷積核方面，需要構建一個三維的調制濾波器，其維度為N×1×M，調制濾波器有N個通道，每個通道是尺寸為1×M的二維濾波器。其中，M與每個原始一維卷積核包含的數據量一致。因此，假設已有L個隨機初始化的原始卷積核，基于維度為N×1×M的調制濾波器，即可生成N×L個維度為1×M的衍生卷積核。此時，每個卷積層均共享使用同一個調制濾波器，網絡參數得以大幅壓縮。

MCNN按下式計算：

基于調制濾波器的調制過程如圖4所示。

圖4 基于調制濾波器的調制過程Fig.4 Modulation process based on modulation filter

基于OFDM系統的多載波調制特征，在原濾波器的正弦函數基礎上，預先定義了調制濾波器［25］，同時利用多個初始相位和頻率來產生調制濾波器，計算式如下：

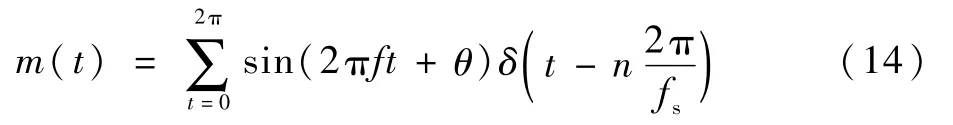
式中：fs為采樣頻率；θ為初始相位；δ為采樣脈沖。

3.2.2 BiLSTM網絡單元結構

本文采取BiLSTM網絡用于預測多徑信道系數，其主體結構為2個單向LSTM網絡。圖5為BiLSTM的網絡結構示意圖，BiLSTM為雙向循環神經網絡，其主體結構是2個單向循環網絡。

圖5 BiLSMT網絡結構Fig.5 BiLSTM network structure

在每個時刻t，輸入會同時提供給這2個方向相反的循環網絡，2個網絡獨立進行運算，各自產生新的狀態和輸出，而BiLSTM的最終輸出就是這2個單向網絡輸出的拼接，可用下式表示：

式中：ot為t時刻BiLSTM網絡的正向輸出；o′t為t時刻BiLSTM網絡的反向輸出；outt為BiLSTM在t時刻的輸出；Concat函數將2個矢量按指定維數結合起來。

3.3 網絡輸出層

網絡輸出層輸出的是最終估計的信道系數的實部和虛部，網絡隱藏層通過全連接神經網絡將BiLSTM網絡的輸出進行維度變換，對所有輸入元素進行加權和，將實部和虛部加在一起得到最終輸出。由于本文采用的信道模型為9徑TDL模型，則網絡輸出為

3.4 網絡訓練與應用

本文中的信道估計網絡主要分為離線訓練和在線測試2部分，如圖6所示。

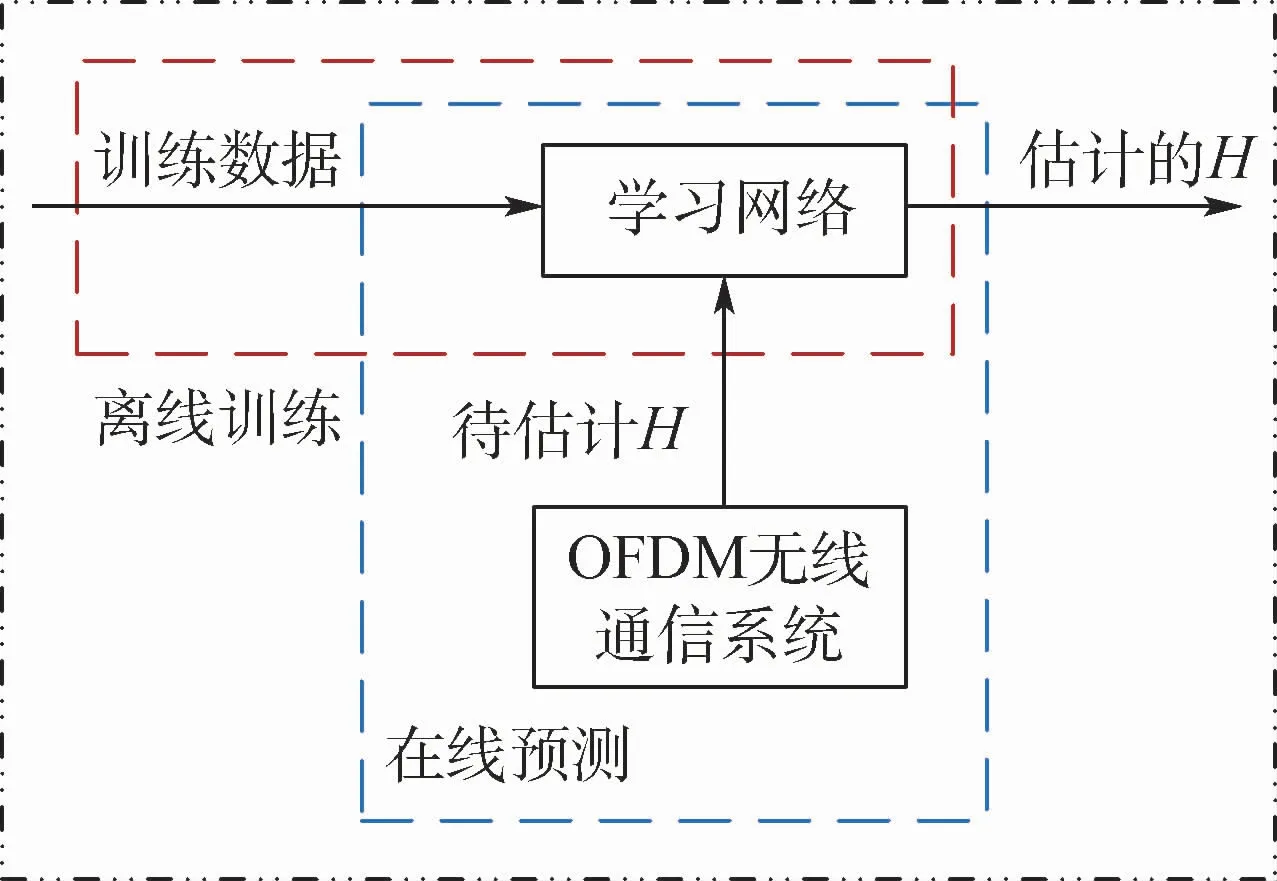
圖6 MC-BI網絡模型的訓練與應用Fig.6 Training and application of MC-BI network model

在離線訓練階段，利用大量空地信道系數數據對學習網絡進行訓練，使MC-BI網絡能夠學習到反映信道延時、衰減等相關參數的高維特征。在在線應用部分，將訓練好的MC-BI網絡應用在OFDM通信系統中。

本文利用端到端的方式訓練得到信道估計網絡中的所有權重和偏置，使用ADAM算法更新網絡的參數集，通過訓練網絡使得MC-BI網絡估計得到的信道估計值與信道真實值的差異最小化，因此MC-BI網絡模型采用的損失函數為均方誤差（mean squared error，MSE）函數，預測損失Loss為

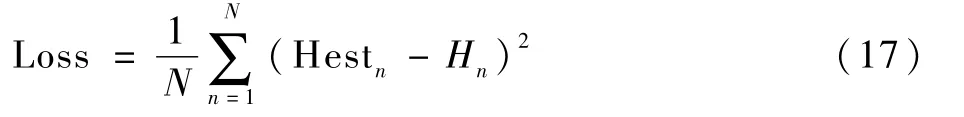
式中：Hestn為信道估計值；Hn為信道真實值；N為信道樣本數。

4 實驗結果

4.1 信道建模場景設置

根據文獻［15-17］，本文選取郊區、山區和海上3種典型場景，建立了準靜態［26］多徑空地信道模型。準靜態信道是一種隨時間緩慢變化的信道，即在一個OFDM幀內信道是不變的，不同幀之間的信道是相互獨立的。3種場景信道模型參數如表1所示。

利用表1中的場景參數，建立空地信道系數樣本集，作為MC-BI網絡的樣本訓練集和測試集。相關生成代碼和樣本數據已開源，參見https：//github.com/liuchunhui2134/AGChannelSimulation。

表1 信道模型參數Table 1 Channel model parameters

4.2 系統參數設置

本文所提的學習網絡模型，MCNN設置為2層，BiLSTM設置為3層。在MCNN網絡中，調制濾波器的維度為5×1×8，原始卷積核的數量為8個。對于離線訓練過程，使用的訓練集和測試集的樣本數分別為10 000和1 000，訓練學習率為0.005。OFDM系統的主要參數設置如表2所示。

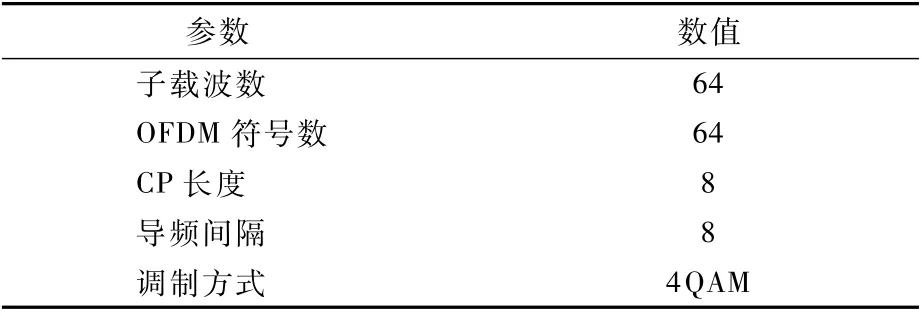
表2 OFDM系統參數設置Table 2 OFDM system parameter setup

4.3 系統接收均方誤差分析

如圖7所示，比較了LS算法［3］、LMMSE算法［5］、現有的全連接DNN網絡［9］和本文提出的MC-BI網絡在不同信噪比（signal to noise，SNR）下3種典型場景時空地信道估計的歸一化均方誤差（normalized MSE，NMSE）性能。

從圖7中可以看出，在3種典型場景下，本文提出的MC-BI網絡的估計精度要優于其他算法，在各種信噪比條件下，比LMMSE算法高2個數量級，比LS算法高近5個數量級；相比于MC-BI網絡，全連接DNN網絡的估計性能次之，LMMSE算法由于利用信道的先驗統計信息使得估計精度優于LS算法；計算復雜度最低的LS算法獲得的NMSE性能最差。

4.4 系統接收誤碼率分析

OFDM系統接收端的誤碼率（bit error ratio，BER）性能是衡量OFDM空地數據鏈系統信道估計性能的重要指標。如圖8所示，比較了不同信噪比下3種典型場景時傳統LS算法［3］、LMMSE算法［5］、全連接DNN網絡［9］和本文所提的MC-BI信道估計算法的BER性能。

圖8 三種典型場景下不同信道估計算法的BER曲線Fig.8 BER curves of different channel estimation algorithms in three typical scenes

從圖8可以看出，3種典型場景下，空地信道環境下各種估計算法的BER曲線隨著信噪比的增加呈下降趨勢；本文提出的MC-BI網絡獲得的BER性能最接近真實信道的BER理論上限值（“True-H”曲線為采用真實信息系數計算出的BER結果），說明本文提出的信道估計網絡在空地數據鏈系統下能夠更好地利用導頻信息實現空地信道估計。

4.5 MCNN網絡的壓縮分析

為了實現模型參數壓縮，本文將調制濾波器技術引入CNN網絡中，生成MCNN網絡。圖9為卷積層數為1、2、3、4時模型壓縮前后的參數量對比。可以看出，隨著卷積層數的增加，與CNN模型相比，MCNN模型的參數量逐漸減少。

圖9 壓縮前后模型參數量比較Fig.9 Comparison of model parameters before and after compression

圖10為山區場景下2層MCNN+3層BiLSTM結構與2層CNN+3層BiLSTM結構的信道估計BER性能曲線。可以看出，將調制技術引入CNN網絡之后，2層MCNN+3層BiLSTM結構與2層CNN+3層BiLSTM結構的信道估計BER性能幾乎相當。這表明本文提出的MCNN網絡結構，與相同層數的CNN網絡結構相比，特征提取能力相近，而模型參數量更少。

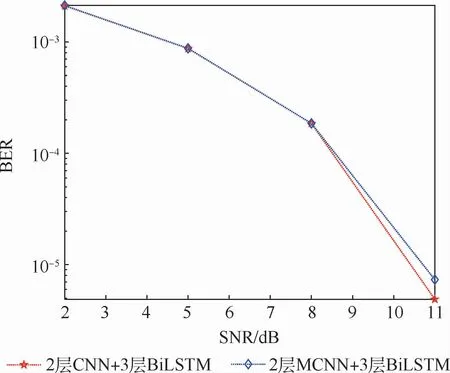
圖10 MCNN+BiLSTM與CNN+BiLSTM網絡BER對比Fig.10 BER comparison between MCNN+BiLSTM network and CNN+BiLSTM network

4.6 網絡層數對實驗結果的影響分析

為了探究網絡層數對MC-BI算法信道估計精度的影響，本節對具有不同MCNN和BiLSTM層數的網絡進行了比較。圖11為在不同MCNN、BiLSTM層數下，MC-BI網絡在山區場景下OFDM地空數據鏈系統中的BER性能。

圖11 不同BiLSTM層與不同MCNN層結合的MC-BI算法的BER曲線Fig.11 BER curves of MC-BI algorithm with different BiLSTM layers and MCNN layers

從圖11（a）可以看到，在MCNN為1層時，選取3層BiLSTM的MC-BI網絡BER性較好；從圖11（b）可以看到，在MCNN為2層時，選取3層BiLSTM的MC-BI網絡BER性能較好；從圖11（c）可以看到，在MCNN為3層時，選取2層BiLSTM的MC-BI網絡BER性能較好。

圖12為1層MCNN+3層BiLSTM、2層MCNN+3層BiLSTM和3層MCNN+2層BiLSTM三種不同結構的BER性能曲線。可以看出，針對本文建立的空地信道樣本，2層MCNN與3層BiLSTM結合的MC-BI網絡的BER性能相對最好。

圖12 三種MC-BI網絡的BER比較Fig.12 BER comparison of three MC-BI networks

綜合以上分析，適當增加網絡層數可以提高MC-BI網絡的估計精度，而過多地增加層數反而降低了估計精度，其原因在于：隨著MCNN和BiLSTM層數的增加，網絡參數增多，模型訓練出現了一定程度的“過擬合”現象。

5 結 論

本文提出了一種基于MCNN和BiLSTM的MC-BI網絡用于信道估計，在空地高速數據鏈OFDM中進行信道估計實驗驗證，得到如下結論：

1）通過構建MC-BI網絡對OFDM多徑空地信道進行估計表明，與傳統LS算法、LMMSE算法及DNN網絡進行比較，本文算法均獲得最佳的NMSE和BER性能。

2）通過引入調制濾波器技術，生成的MCNN網絡有效實現模型參數壓縮，且特征提取能力與原CNN網絡相當。

3）通過對比不同網絡層數的BER性能，表明適當增加MCNN和BiLSTM的層數可以提高MC-BI網絡估計的BER性能。

本文提出的基于MCNN的空地數據鏈信道估計方法對于“準靜態”空地信道的估計性能較好，然而由于無人機等空中平臺的飛行姿態多變、飛行速度多樣，空地信道估計問題還需考慮存在機身衰落、信道快時變性等因素的影響。因此，建立更加符合實際的空地信道樣本數據，進一步優化信道估計網絡結構將是下一步研究的重點。