機載中空纖維膜組件殼程氣體流動數值模擬
劉國田,白文濤,潘江麗,陳廣豪,潘俊,馮詩愚,*
(1.南京航空航天大學 航空學院 飛行器環境控制與生命保障重點實驗室,南京 210016;2.中國航空工業集團有限公司 南京機電液壓工程研究中心 航空機電系統綜合航空科技重點實驗室,南京 211106)
中空纖維膜具有單位體積裝填密度高、占地面積小、分離效果好等特點,被廣泛應用于氣體分離、海水淡化、水處理及生物醫學工程等方面。因氧氣和氮氣在膜絲上滲透速率存在差距,在膜絲內外氣體分壓力差的驅動下,氧氮可以實現分離,從而在膜絲兩側形成富氮和富氧氣體。飛行器燃油箱機載惰化系統利用中空纖維膜組件產生富氮氣體,并將富氮氣體引入油箱中來降低油箱氧濃度,從而實現達到防火抑爆的目的[1-5]。
雖然通過試驗方法來測量膜組件的性能是最為常見的方法,但是試驗代價高,周期長。因此,近年來已經有大量采用數值計算方法來獲取膜組件性能的研究。最為常見的研究是分析不同膜絲內側操作參數和結構參數對分離性能的影響,如Ahmad[6]和Marcos[7]等采用數值方法研究了膜絲的濃差極化分布。Parvareh等[8]研究了壓力對微濾膜滲透通量的影響。卞銳和許松林[9]利用數值模擬軟件研究了入口速度和管徑對中空纖維式滲透汽化膜內流動特征及分離性能的影響。Ardaneh等[10]建立二維數學模型研究了進口原料質量流量、壓力及膜絲長度對氣體分離效率的影響。這些研究中大多對膜絲外側即殼側進行了簡化處理,認為殼程的流動差異不會影響分離過程。
顯然,殼程中由于膜絲的分布可能存在不均勻等現象,殼程各處的濃度分布也會有差別,這將導致分離存在差異。顯然,了解殼程的流動情況可以更加精確地預測膜組件的分離效果。楊毅等[11]利用隨機順序添加算法創建了膜組件的三維數學模型,研究了膜絲軸向的非平行分布對組件徑向局部溝流和死區的影響。Buetehorn等[12]對不規則纖維排列組件單元進行了計算流體力學(CFD)方法模擬。吳云等[13]利用數值模擬的方法研究了不同填充方式下生物膜反應器內流場特性。Costello等[14]對不同排布方式的中空纖維膜組件進行了殼程流動阻力系數的實驗測量,結果表明不均勻排布阻力系數明顯小于均勻排布時的阻力系數。Cai等[15]模擬了中空纖維膜殼側流動和組件整體傳質特性。Ma等[16]模擬了膜纖維間距和位置對不同位置纖維的過濾性能的影響。這些研究表明,殼程中介質的流動和濃度分布差異不應當被忽略。
上述研究中均為液膜,目前國內外鮮有氣體分離膜殼程流動分布的研究報道,其主要原因在于氣體黏度小,流動阻力低。因此,殼程的不均勻性對民用氣體膜組件分離影響較低。然而,機載膜組件所要求的尺寸小,操作強度大,填充密度高,加之隨著飛行高度變化,殼程氣體密度急劇降低,體積流量增加,因此迫切需要掌握殼程中氣體的流動情況。鑒于此,采用CFD方法對燃油箱惰化用機載中空纖維膜組件殼程進行建模仿真,分析不同工況下的組件殼程氣體流動分布情況。在相同條件下,膜絲束間距、膜絲束排布方式和飛行高度會影響氣體在膜絲束間和組件內壁處流動量的比值,但膜絲束入口速度對比值影響較小,這些結論為機載膜組件設計和相關研究提供參考。
1 模型和計算
1.1 計算模型的建立
以某中空纖維膜組件為研究對象,幾何結構參數如下:組件外徑為300 mm,長度為690 mm,膜絲外徑為0.16 mm,因填充密度不同,組件含有膜絲幾萬到十幾萬根,膜組件圓形出口半徑為10 mm,圓心距離上端口60 mm。考慮建模的可行性和網格數量的經濟性,在此實物基礎上進行了如下模型簡化:①組件中膜絲以千根膜絲捆扎成膜絲纖維束的形式存在,膜絲束半徑R=3 mm;②膜絲束排布均勻,膜絲束間距L為相鄰兩束圓心距離減去兩圓半徑;③膜絲在軸向直線分布,不存在彎曲和變形。基于以上假設簡化,在CATIA中建立簡化模型,如圖1所示。

圖1 膜組件幾何模型Fig.1 Geometric model of membrane module
1.2 網格劃分和模型求解
將CATIA模型導入ICEM CFD中進行非結構化體網格劃分,模型采用八叉樹方法生成四面體混合網格,在膜絲和出口處采用較為細致的網格結構,其三維非結構網格如圖2所示。
圖2 膜組件三維非結構網格Fig.2 Unstructured 3D mesh of membrane module
采用定常穩態方法模擬中空纖維膜組件殼程氣體流動狀況。建立組件的幾何模型和劃分三維體網格后,用FLUENT求解流場的連續性方程和動量方程組:

式中:下標1、2分別為進口、出口參數;Vn為垂直于截面方向的速度;ρ為氣體密度;A為截面面積;ˉv為氣體速度向量;f為質量力;pn為表面力。
在FLUENT中,將膜絲束外表面設為速度入口,組件出口邊界類型為壓力出口,組件外壁的邊界類型為壁面。以二階迎風格式離散方程,采用基于壓力的絕對速度方程、標準k-ε湍流模型并利用SIMPLE算法求解流場。
1.3 網格無關性驗證
為驗證模型網格無關性,將模型分別劃分為150萬、400萬、650萬數量網格,以出口截面面積加權平均速度vout為檢驗標準,網格無關性驗證結果如圖3所示。由圖3可知,網格數量對出口平均速度值影響不大。綜合考慮計算的精度和效率,網格數量選取為400萬。
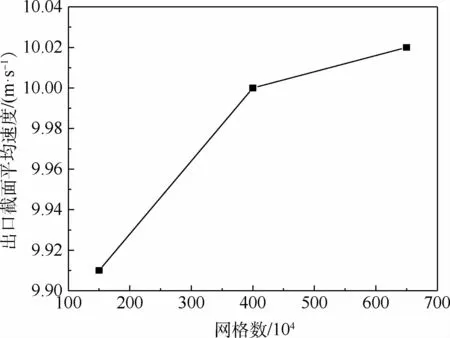
圖3 網格無關性驗證Fig.3 Gird independence verification
2 工況條件和截面平均速度比定義
2.1 工況條件
借鑒文獻[11-16]研究,膜組件殼程的流動影響因素有組件的膜絲束排布方式和填充個數、膜絲束入口速度、流量等。考慮所研究的膜組件用于機載惰化中,因而需要考慮飛行高度變化帶來的環境壓力的改變。因此,進行了不同工況下的幾何建模和數值計算。
1)保持膜絲束入口速度不變,改變膜絲束間距L,隨著膜絲束間距的改變,膜絲束填充數隨之改變。當L分別為3.0R、2.5R、2.0R、1.5R、1.0R時,對應的膜絲束填充個數為32、52、60、80、112。
2)保持膜絲束入口質量流量不變,隨著膜絲束間距的增大,出口速度增大。當L分別為3.0R、2.5R、2.0R、1.5R、1.0R時,對應的膜絲束入口速度為0.010 5、0.006 5、0.005 6、0.004 2、0.003 m/s。
3)保持膜絲束間距不變,更改膜絲束入口速度為0.003、0.005、0.007、0.009、0.011 m/s。
4)保持膜絲填充個數不變條件下,比較膜絲束均勻排布和不均勻排布流動,分析排布方式對流動特性的影響,如圖4所示。其中不均勻排布是幾何建模型時,手動劃分填充同數量不相交膜絲束。

圖4 膜絲束排布方式Fig.4 Arrangement mode of membrane tows
5)在保持膜絲入口速度為0.003 m/s、膜絲填充數量為80、膜絲均勻排布時,定義膜組件出口壓力為環境背壓,改變出口背壓,模擬計算飛行高度為2 000、5 000、7 000 m時的工況。在對流層中,大氣環境壓力與高度的關系為

式中:ph為不同飛行高度上的壓力,Pa;p0為海平面大氣壓力,p0=101 325 Pa;h為飛行高度,m;g為重力加速度,g=9.8 m/s2;α為年平均溫度直降率,α=0.006 5℃/m;r為氣體常數,r=287 J/(kg·K)。在飛行高度h為2 000、5 000、7 000 m時,對應的大氣環境壓力為79 504、54 001、41 078 Pa。
2.2 截面平均速度比定義
以軸向不同截面進行氣體流場分析,在每一截面上以一個包圍所有膜絲束的虛擬圓將截面分成內圓和圓環2個面,如圖4所示,其中虛擬圓半徑為55 mm,內圓為膜絲束間部分,圓環為組件內壁部分。并定義截面平均速度比θ(無量綱)來描述殼程氣體流動分布情況,表示為

3 計算結果分析
膜絲束間距為1.5R,膜絲束表面速度設為0.003 m/s時,組件軸向截面速度v和壓力p的云圖如圖5所示。由圖5可以看出,速度和壓力在出口處變化急劇,在組件內變化較小。組件內壓力速度變化小是因為組件中氣體流速慢,此外氣體黏度小,流動阻力低,流動損失小;出口處速度壓力變化劇烈是因為流動截面的急劇收縮。其他工況下速度、壓力云圖趨勢與之相似。
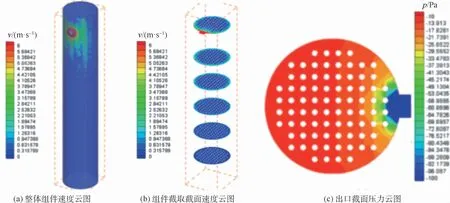
圖5 膜組件速度和壓力云圖Fig.5 Velocity and pressure contour of membrane module
3.1 膜絲束間距對殼程氣體流動分布的影響
入口速度不變,不同L下的θ值如圖6所示。由圖6可見,保持膜絲束入口速度為0.003 m/s時,截面平均速度比θ隨著膜絲束間距的減小先減小后增大,在間距為1.5R時候達到最小值。
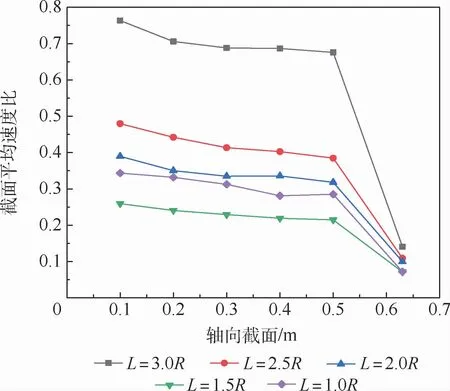
圖6 入口速度不變時不同L下的θ值Fig.6 Values ofθfor different L with constant entrance velocity
在入口流量不變的情況下,不同L下的θ值如圖7所示。由圖7可知,與膜絲束入口速度不變下相似,在膜絲束保持入口質量流量為定值時,截面平均速度比θ隨著膜絲束間距的減小先減小后增大,在間距為1.5R時候達到最小值。這是因為:在膜絲束間距較大時,膜絲束間的距離尺寸與組件內壁處縫隙尺寸相近,膜絲束間的軸向流動阻力與組件內壁處的軸向流動阻力量級相當,而隨著膜絲束間距的縮小,膜絲束間的軸向流動阻力較大,氣體克服膜絲束間徑向阻力后會涌向內壁處流動,這一過程導致內壁處氣體流動量增大,膜絲束間氣體流量減小,從而使得θ值減小。而膜絲束間距進一步地減小會導致膜絲間的徑向阻力增大,氣體不能克服阻力向組件內壁處流動,從而導致膜絲束間的氣體流動量增大,使得θ增大。

圖7 入口流量不變時不同L下的θ值Fig.7 Values ofθfor different L with constant entrance flow rate
3.2 入口速度對殼程氣體流動分布的影響
保持膜絲束間距不變,增大膜絲束入口速度,不同v下的θ值如圖8所示。由圖8可知,θ值隨v變化不大。這是因為:入口速度微量級的改變,引起的雷諾數變化很小,產生的阻力變化也較小,殼程氣體的流動也不會發生明顯的變動。
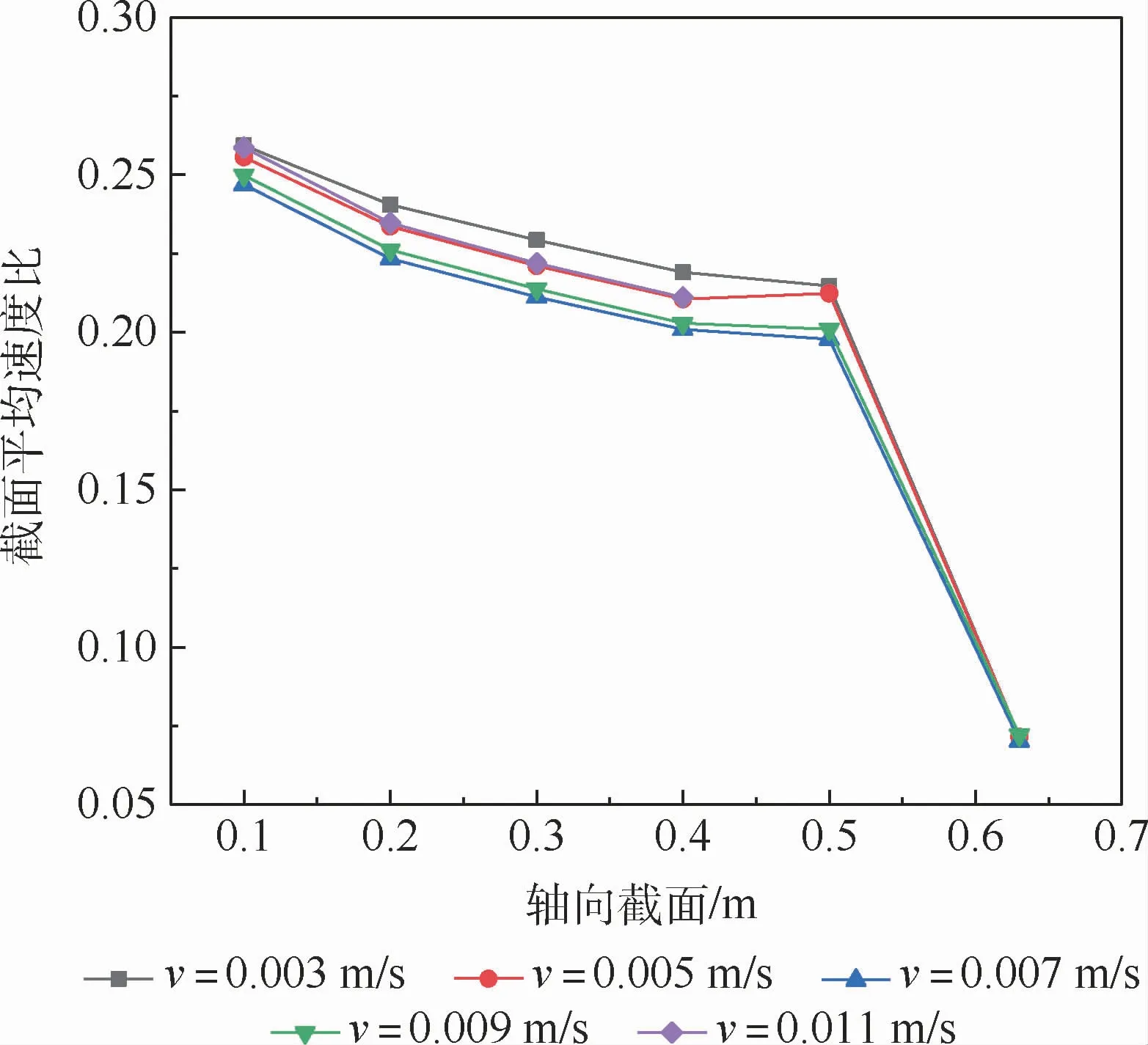
圖8 膜絲束間距不變時不同v下的θ值Fig.8 Values ofθfor different v with constant entrance L
3.3 膜絲束排布方式對殼程氣體流動分布的影響
對膜絲束填充數為60、80的2個模型分別進行均勻排布和不均勻排布建模。不同膜絲束排布方式下的θ值如圖9所示。由圖9可見,與均勻排布相比,不均勻排布時的θ更大。這意味著均勻排布時膜絲束間流動的氣體量更少,氣體量少的原因是由于膜絲束間阻力大造成的,這與Costello等[14]的研究結果一致。Costello等[14]對不同排布方式的中空纖維膜組件進行了殼程流動阻力系數的實驗測量,結果表明不均勻排布阻力系數明顯小于均勻排布時的阻力系數,不均勻排布時,組件膜絲束間阻力更小,因為氣體流量更大。
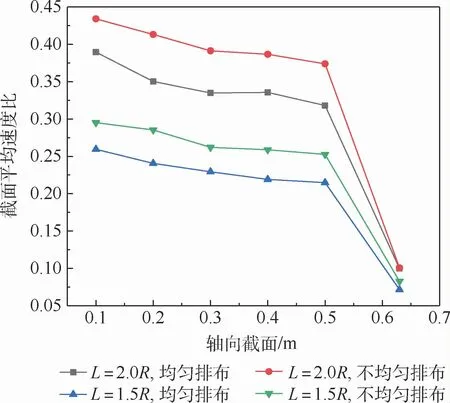
圖9 不同膜絲束排布方式下的θ值Fig.9 Values ofθin different arrangement modes of membrane tow
3.4 飛行高度對殼程氣體流動分布的影響
飛行高度與組件截面、膜絲束間截面平均速度關系如圖10和圖11所示。由圖10和圖11可見,隨著飛行高度的增大,出口背壓減小,組件膜絲束間截面氣體平均流動速度基本保持不變,但是整個膜組件軸向截面平均速度在增大。因此,背壓改變對組件內壁處的氣體流動分布有著重要影響,對膜絲束間氣體流動分布影響不大。
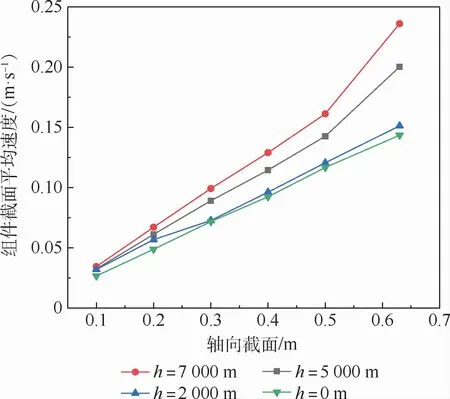
圖10 飛行高度與組件截面平均速度關系Fig.10 Relation between flight height and average section velocity of membrane module
4 結 論
膜分離空氣形成富氮氣體來惰化燃油箱是目前經濟高效的燃油箱惰化技術。采用CFD方法對某中空纖維膜組件殼程氣體流動進行了數值模擬,得到了不同工況下的組件軸向各截面的氣體流動分布,研究結果表明:
1)在膜絲束入口流動速度或膜組件入口流量一定時,截面平均速度比θ隨著膜絲束間距的減小先減小后增大,在間距為1.5R時候達到最小值,此時殼體氣體流動在組件內壁處流動達到最大量。這表明在膜組件設計和使用時,殼程氣流布局與膜絲束間距存在最優設計和選擇。
2)在膜絲束間距不變的情況下,增大膜絲束入口速度對θ值影響不大,因而在實際使用中為了得到更多惰氣量,可以適當增大殼程流量。
3)相同膜絲束填充數量下,不均勻排布時的截面平均速度比θ值比均勻排布的值更大,意味著均勻排布方式更有利于氣體的分離。
4)當飛行高度增大而出口背壓減小時,膜組件軸向截面平均速度增大而膜絲束間截面平均速度變化不大,這表明背壓改變對組件內壁處的氣體流動分布有著重要影響,對膜絲束間氣體流動分布影響不大。

