部分相干啁啾光學相干渦旋晶格在生物組織湍流中的平均光強與光譜位移
程 科,朱博源,舒凌云,廖 賽,梁夢婷
(成都信息工程大學,光電工程學院,四川 成都 610225)
1 Introduction
Biological tissues have complex structures and display abundant spectral behavior in the optical field.The light can be scattered and absorbed when it is transmitted to subcutaneous tissues and organs through the skin.Consequently, the received light carries physiological and pathological information about biological tissues.Some promising technologies have been made for optical noninvasive early diagnosis of biological tissue diseases, such as laserinduced fluorescence, polarized light imaging and elastic-scattering measurement.Schmittet al.explored spatial variation of the refractive index of various mammal tissues and found that their structure functions were analogous with the classical Kolmogorov model in atmospheric turbulence,where the model of the power spectrum refractiveindex in biological tissue was also presented[1].According to this power spectrum model, the changes of coherence and polarization for an electromagnetic Gaussian Schell-model beam in biological tissues were studied by Gaoet al[2], and then their coherences and polarizations for anisotropic electromagnetic Gaussian Schell-model beams were further analyzed by Zhaoet al.[3].In 2021, Zhanget al.studied the average intensity and beam quality of Hermite-Gaussian correlated Schell-model beams in biological tissue, and found that it is less sensitive to tissue turbulence than that of Gaussian Schell-model beams[4].
On the other hand, Optical Coherent Lattices(OCLs) have inspired prominent research interests due to their special periodic reciprocities[5-7].New properties have been found that a Gaussian profile at the source plane gradually becomes a periodic array in the far-field zone.Much effort has been devoted to exploring their propagation properties in atmospheric and oceanic turbulence[8-9].In addition, the effect of the embedded optical vortex or rotating elliptical Gaussian factor on OCLs in a turbulent atmosphere was also studied[10-11].It has been found that the lattice periodicity reciprocity can be preserved over a certain distance even in the atmosphere or oceanic turbulence, and its scintillation index is lower than that of Gaussian beams.The optical coherence lattices can preclude Talbot self-imaging in free space, which is beneficial to robust optical imaging or the transfer of information in biological tissue[6].However their researches are mainly focused on the propagation dynamics of OCLs in the field of monochromatic light, and the spectral behavior of a polychromatic field in biological tissue is not addressed.What happens in the polychromatic light fields of a chirped Gaussian pulse and vortex function if it is brought into OCLs?
The motivation of this paper is to investigate the averaged intensity and spectral shift of Partially Coherent Chirped Optical Coherence Vortex Lattices (PCCOCVLs) in biological tissue turbulence.The results show that optical lattice structures are modulated by lattice parameters and topological charge, and that rapid spectral transitions vanish over a longer distance, which provides valueable applications in developing image recognition technology, medical devices and noninvasive optical diagnoses in biological tissue.
2 Cross-spectral density function and spectral intensity in biological tissue turbulence
Assume that the propagation direction of PCCOCVLs in biological tissue turbulence propagates along thez-axis, whose cross-spectral density at the source plane can be expressed by[12-14]

wherex′j=ρ′jcosθjandy′j=ρ′jsinθj(j=1, 2) are po-sitions of two points atz=0 in the Cartesian coordinate,w0is the radius of the beam waist,Vnsis the power distribution of the pseudo-modes constituting the lattice,ais the lattice constant,mis the topological charge of the vortex,σis the correlation length andNindicates the number of lattice lobes,respectively.In Eq.(1) the incident pulsed beam is assumed to be a chirped Gaussian given by[15-16]
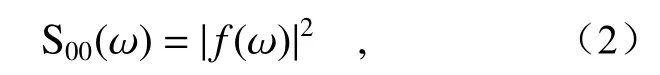
and
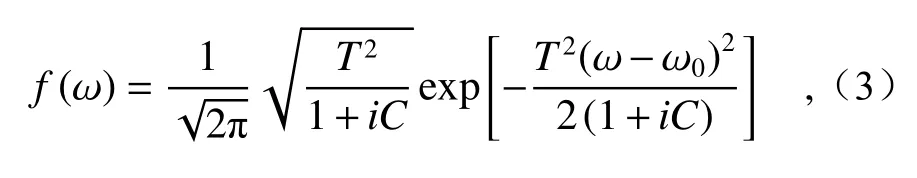
with central frequencyω0, pulse durationTand chirp parameterC.
According to the extended Huygens-Fresnel principle, the cross-spectral density function of PCCOCVLs propagating through biological tissue turbulence can be expressed as
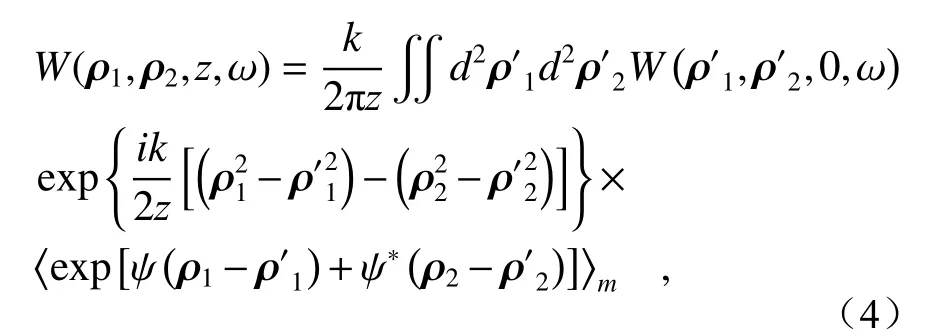
wherek=ω/crepresents the wavenumber related to frequencyωand the speed of light in a vacuumc,ψis the phase function in the refractive-index fluctuations, andρ1=(x1,y1) andρ2=(x2,y2) are position vectors of two points at receiver plane, respectively.The ensemble average of the biological tissue turbulent in Eq.(4) is given by

whereρ0is the spatial coherence length of a spherical wave in biological tissue turbulence, which takes the form of[17-19]
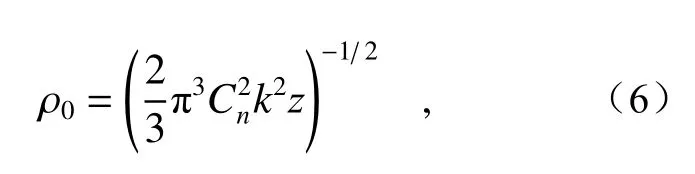
Substituting Eqs.(1)-(3) into Eqs.(4)-(6), and lettingx1=x2=xandy1=y2=yin the Cartesian coordinate, the analytical spectral intensity of PCCOCVLs propagating through biological tissue turbulence at the receiver plane is expressed as
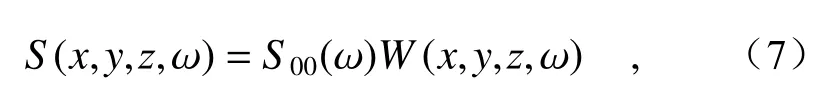
where
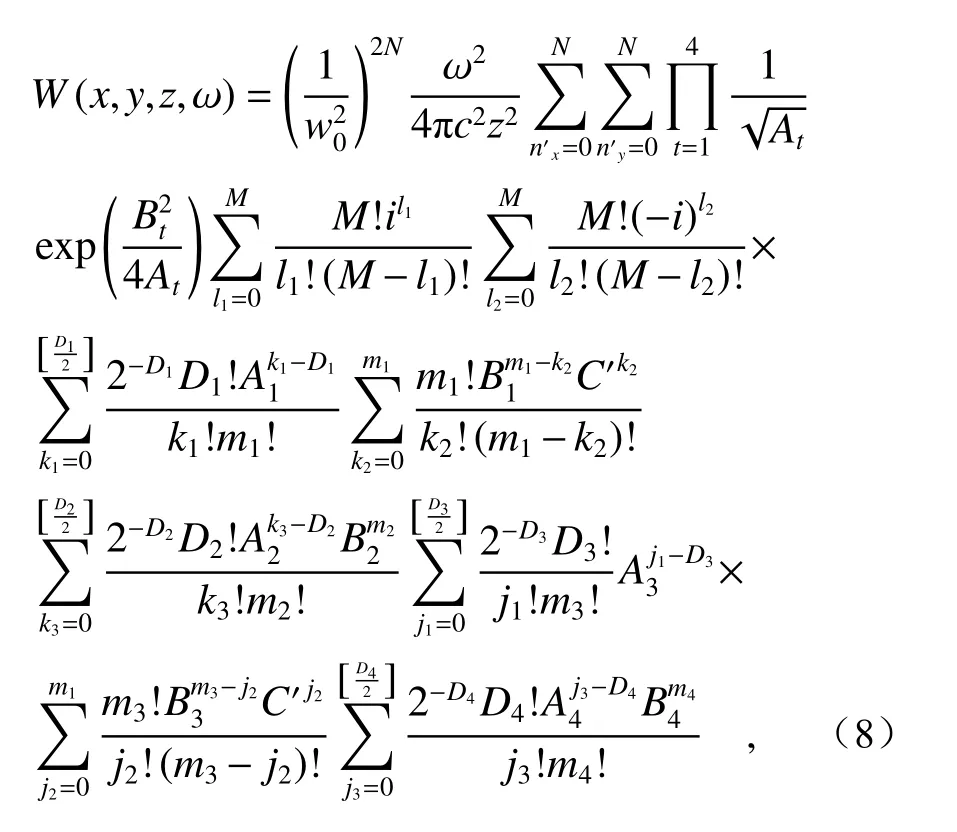
with
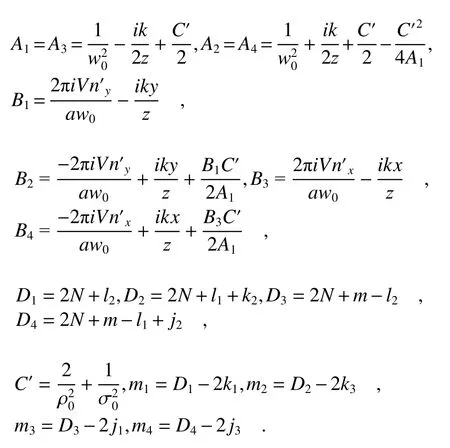
In monochromatic lightof ω=ω0=2πc/λ0, the Eq.(8) denotes the averaged intensity of the PCCOCVLs in biological tissue.For the polychromatic light fields, the Eq.(8) describes the spectral intensity of PCCOCVLs, which depends on lattice constanta, observation point (x,y,z), pulse durationT, chirp parameterCand biological tissue turbulence parameters.
The frequencyωmaxof the maximum spectral intensities for the PCCOCVLs are determined by
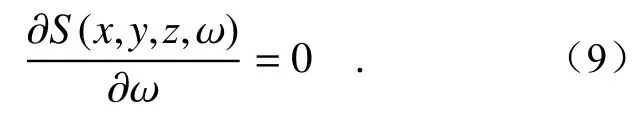
The relative spectral shift is described by
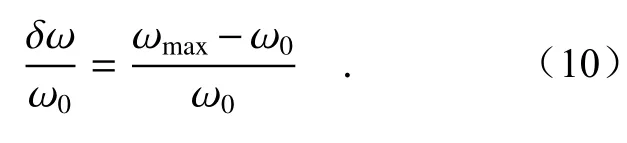
Ifδω>0, the spectrum is blue-shifted, whereas it is red-shifted forδω<0.
We choose a human upper dermis, a mouse's deep dermis and a mouse's intestinal epithelium as the specimens for numerical calculation.The refractive indices of the biological tissues areCn2=0.06×10-3μm-1,Cn2=0.22×10-3μm-1, andCn2=0.44×10-3μm-1[17], respectively.Numerical calculations are performed to illustrate the influence of pulse durationTand chirped parameterC, observation point (x,y,z) and the biological tissue turbulence parameters (i.e.Cn2) on the spectral behaviors of PCCOCVLs.The calculation parameters are fixed byλ0=0.83 μm,σ=2 μm,z=1.5 cm,ω0=2 πc/λ0,w0=5 mm,Cn2=0.22×10-3μm-1,T=2fs,C=2,N=2,m=2 andc=3×108m/s unless otherwise specified.
3 Averaged intensity and spectral shift
Fig.1 (Color online) gives the intensity evolution of PCCOCVLs with monochromatic light in biological tissue for different lattices parametera.It is found that the beam at the source plane ofz=0 presents an annular structure with a vortex core and that it gradually evolves into a periodic array of lobes with a dark zone at its origin as the distance increases.As the distance further increases, the turbulence effect in biological tissue continues to accumulate, the profile of the annular structure and the array eventually disappear and become a Gaussian pattern.Although the patterns are the same at the source plane for different lattice parameters, a larger lattice parameter changes circular array to a rectangular structure in propagation.It should especially be noted that the dark lines in the last line of Figs.1 (b)-(d) are not edge dislocations.
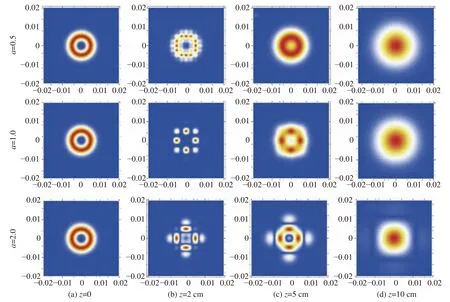
Fig.1 Intensity evolution of PCCOCVL beams with monochromatic light in biological tissue for different lattices parameter a
Fig.2 (Color online) describes the intensity profiles of PCCOCVLs with monochromatic light in biological tissue for different topological chargesmwith canonical (a=1) and noncanonical lattices parameters (a=1+i).Where there is a vortex, it can be seen that noncanonical lattices parameters lead to an annular structure with periodic lobes, and the dark zone at the origin increases with an increasing topological charge.For the case of non-vortex, the noncanonical lattices parameter ofa=1+iexhibit a periodic array (e.g.3×3 spot array) rather than that of canonical lattices ofa=1.The results show that lattice parameters and topological charge change dramatically with changes in the structures of periodic arrays.
To further investigate the spectral behavior of polychromatic light, Fig.3 shows a relative spectral shift of the PCCOCVL beams over the transverse coordinatexfor different lattices parameters.One can see that their spectrums are not influenced by lattices parameters, and the spectrum becomes redshifted with an increase in the transverse coordinatex.When the propagation distance in biological tissue is small (e.gz=1 or 2 cm) it is found that there is a rapid spectral transition at the critical value ofxc=1.06 cm, and the changes of Δ(δω/ω0) are 0.9 and 0.6 forz=1 and 2 cm, respectively.As the beam further propagates in biological tissue, the spectrum becomes more flat.
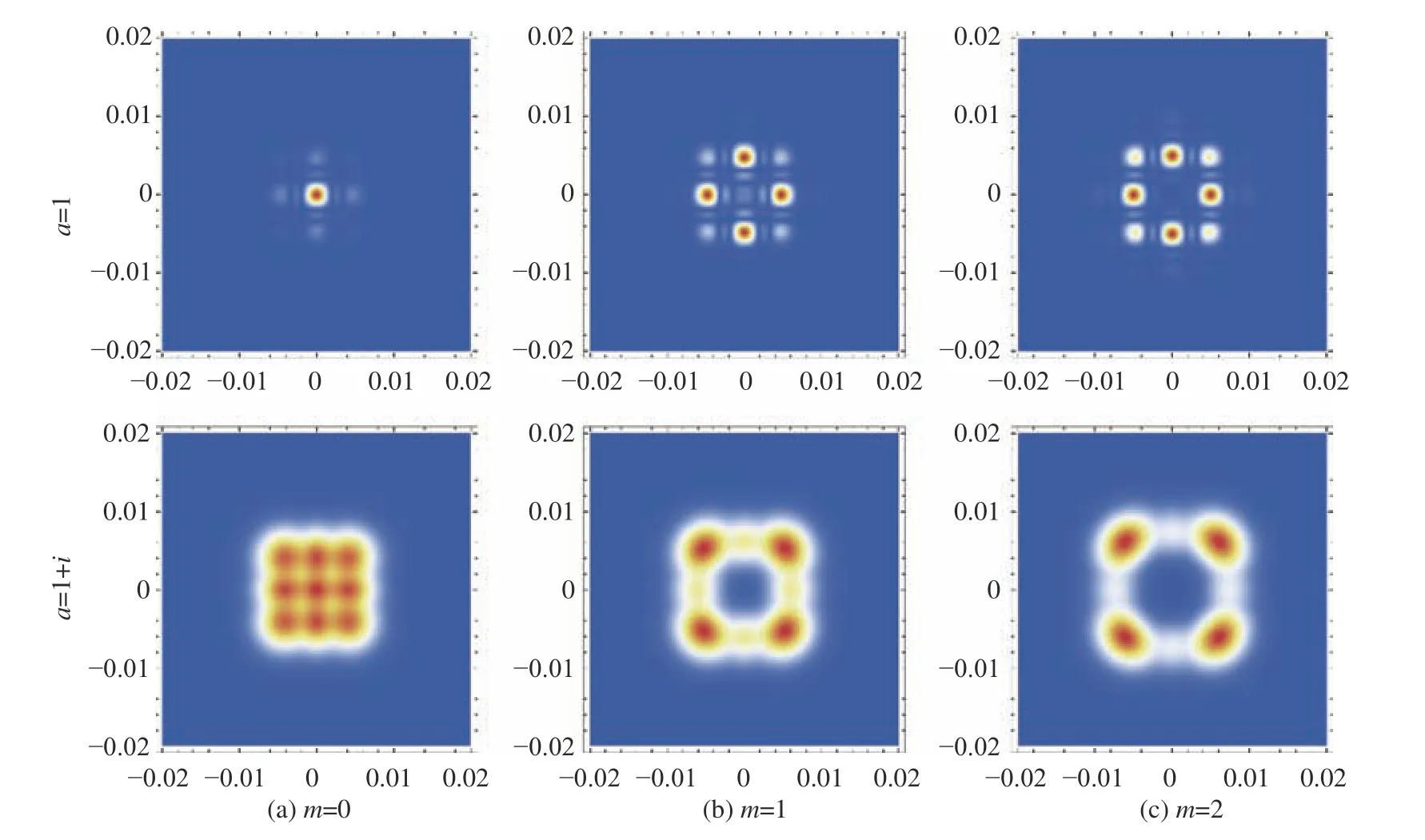
Fig.2 For canonical and noncanonical lattices parameters, the intensity profile of PCCOCVL beams with monochromatic light in biological tissue for different topological charge m
Here, our focus is given to rapid spectral transition.Fig.4 (Color online) plots the relative spectral shift of PCCOCVLs versus transverse coordinatexfor differentCandTatz=2 cm.It is found that there exist critical valuesxcof spectral transition,and these values decrease with the increase of chirp parameterCand the decrease of pulse durationT.For example, the critical values ofxcare 8.6 mm,14.7 mm and 19.4 mm forC=0, 1 and 3, respectively.In addition, the red-shift spectrum is presented at a smaller transverse coordinatex, and its value decreases and then rapidly increases with an increase in coordinatex.The phenomenon means that the spectrum is sensitive to the transverse coordinate for differentCandT, which is significant in the detection and acquisition of spectrum signals in biological tissues.

Fig.3 Relative spectral shift of the PCCOCVLs versus the transverse coordinate x for different lattices parameter a
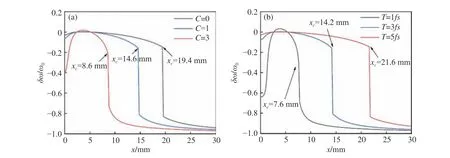
Fig.4 Relative spectral shift of the PCCOCVLs beam versus the transverse coordinate x for different C and T
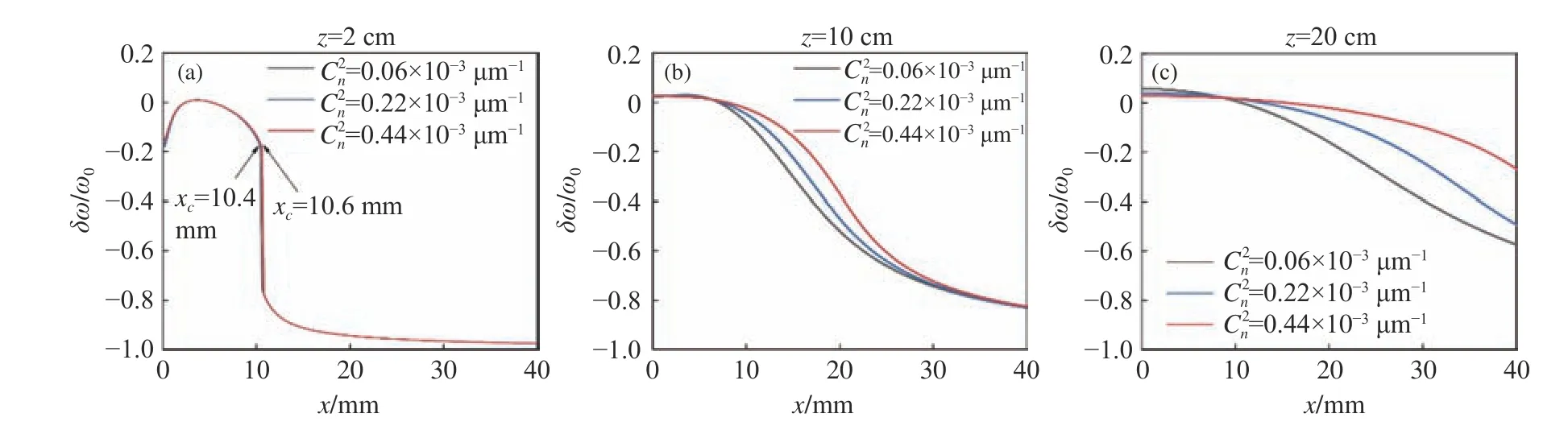
Fig.5 Relative spectral shift of the PCCOCVL beam versus transverse coordinate x for different biological tissue turbulences
Fig.5 (Color online) gives the relative spectral shifts of the PCCOCVL beam versus transverse coordinatexfor different biological tissue turbulences(i.e.Cn2).When the propagation distance in biological tissue is small, the turbulence-induced spectral difference is not significant, and their spectral behaviors in red-shift zone are similar to those of Fig.4.The rapid spectral transition disappears, to be replaced by a smooth curve in the spectrum when the beam travels a longer distance in the biological tissue, e.g.z=10 cm orz=20 cm.At the same transverse coordinate, stronger turbulence leads to a smaller red-shift value in the spectrum, which indicates that the accumulated turbulence effect in a longer distance can suppress not only spectral transition, but also spectral shift.
Fig.6 (Color online) gives physical explanations for the rapid spectral transition of PCCOCVL beams where the critical coordinatexc=14.6 cm andC=1 as shown in Fig.4(a).One can see that there exists only one spectral maximumSmax1at (ωmax1-ω0)/ω0=-0.16 in Fig.6(a), but two spectral maximumsSmax1andSmax2are found at (ωmax1-ω0)/ω0=-0.16 and(ωmax2-ω0)/ω0=-0.8 at critical transverse coordinatexc=14.7 cm as shown in Fig.6(b).The second spectral maximumSmax2continues to maintain its previous maximal value, but the spectrum ofSmax1is suppressed for the coordinatex=14.8 cm.The behavior is the result of spectral competition in two red-shift spectra.If one of them has a disadvantage, then the other presents superiority in the spectrum.
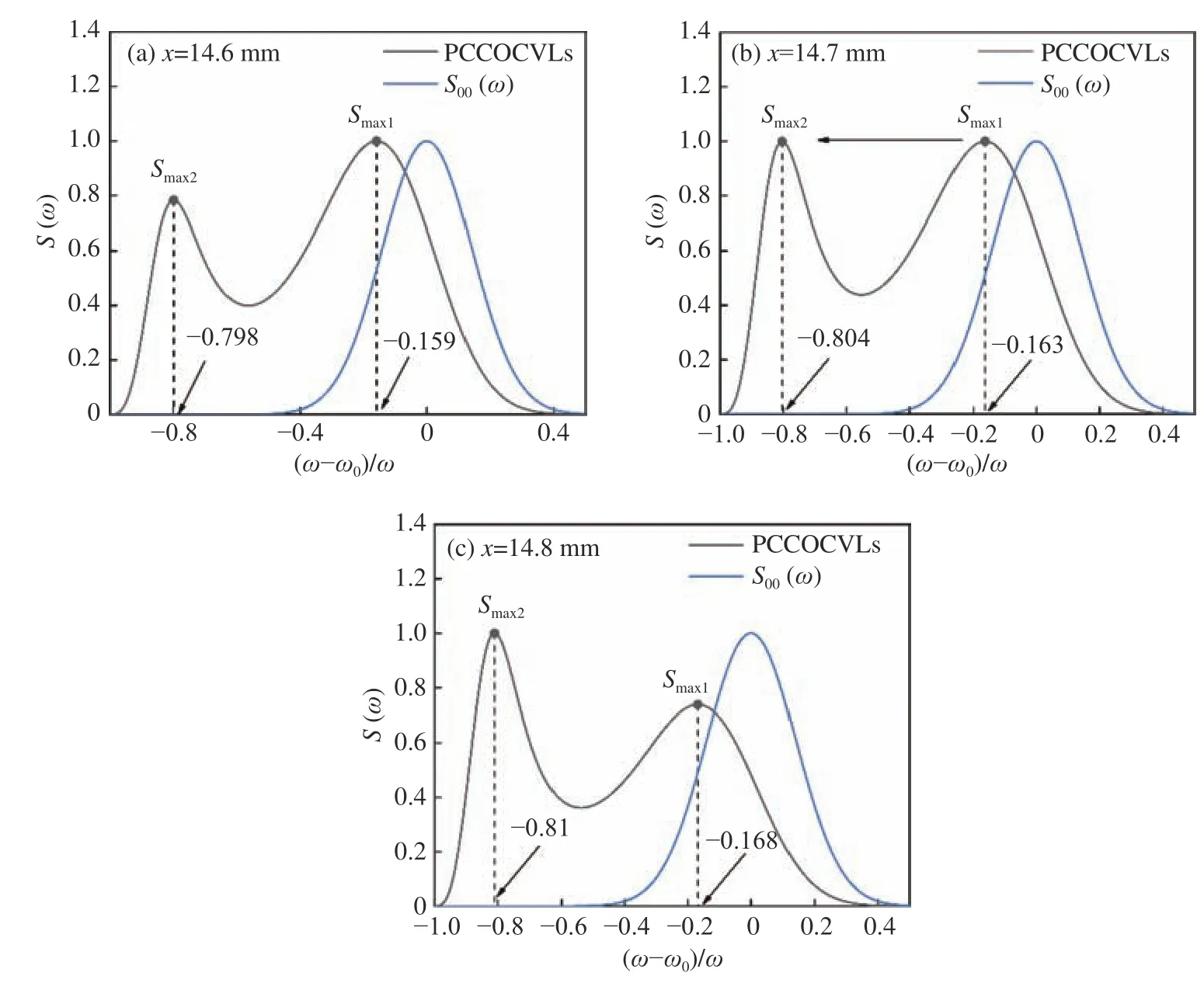
Fig.6 Physical explanations of the rapid spectral transition of PCCOCVLs in xc=14.6 cm and C=1 of Fig.4 (a)
4 Conclusion
Intensity evolution and spectral behavior of PCCOCVLs passing through biological tissue turbulence are investigated by using the extended Huygens-Fresnel principle.The analysis of the evolution of its intensity shows that the beam in the monochromatic optical field evolves from an annular structure profile with a vortex core into a periodic array of lobes with a dark zone, and it finally presents a Gaussian-like structure when the distance in biological tissue increases.Moreover, the noncanonical lattices parameter ofa=1+ileads to an annular structure with periodic lobes where there is a vortex, while a non-vortex presents a periodic array rather than that of canonical lattices wherea=1.These results indicate that lattice parameters and topological charges change dramatically according to the structure of the periodic array, and the cumulative effect of turbulence in a longer distance results in the disappearance of optical lattices and the appearance of a Gaussian-like pattern.
However, in a polychromatic optical field, the effect of lattice parameters on spectral shift is negligible.Although the spectrum in red-shifts smoothens with an increasing distance, it presents a rapid transition for a smaller distance.There are some critical transverse coordinates in spectral rapid transitions, whose decreases are accompanied by an increase of chirp parameterCand a decrease of pulse durationT.The influence of cumulative turbulence in a longer distance on spectral behavior results in the disappearance of the rapid spectral transition which is replaced by a smooth curve in the spectrum.Stronger biological tissue turbulence in a longer distance suppresses the spectrum shift and spectral transition.The appearance of rapid spectral transitions in PCCOCVLs is also physically explained by spectral competitions.
Refs.[4, 8, 9] investigated the lattice profile and spatial degree of coherence in atmospheric or oceanic turbulence and studied the polarization behavior and intensity in biological tissue turbulence.In contrast, where we focus the introduction of a chirped Gaussian pulse and a vortex function to the optical coherence lattices in polychromatic light field, and its sensitivity to spectrum signals such as rapid spectral transitions and spectral shifts in biological tissue.The results obtained here should be useful for the noninvasive optical diagnoses including the detection and acquisition of spectrum signals in biological tissue.

